毛坯开槽方式中零件加工变形的演变机理与控制方法
2022-05-05王华敏秦国华吴铁军
王华敏,陶 江,秦国华,林 锋,吴铁军,郑 许
(1. 南昌航空大学航空制造工程学院,南昌 330063;2. 东莞职业技术学院机电工程系,东莞 523808;3. 南京航空航天大学机电学院,南京 210016;4. 中南大学材料科学与工程学院,长沙 410083;5. 广西南南铝加工有限公司,南宁 530031)
随着航空制造业的不断发展,对现代飞机和航天器等性能的要求不断提高,整体结构件被越来越多地应用到实际生产当中。整体结构件外表光滑,重量轻,在刚度、疲劳强度以及各种失稳临界值方面,均比铆接结构更为优秀[1]。整体结构件的应用,是航空制造业的一大进步。但是,由于整体结构件形状更为复杂,材料去除率更高,加工精度要求更苛刻,导致整体结构件在加工过程中,往往伴随着更大的加工变形。加工变形对工件制造精度有着显著影响,是航空制造业的亟待解决的关键问题[2-3]。
从20 世纪90 年代起,空客公司便联合六个欧洲国家开始了变形问题的专门研究,基本实现了仅需依靠数控人员就能解决的操作步骤[4-5]。然而,整体结构件相关技术涉及国防核心技术,相关成果并未对外公开,有严格的知识产权保护。国内工程技术人员也曾与波音公司一起讨论过加工变形的工艺问题,但由于涉密问题均无果而终[6-7]。
航空整体结构件作为大型的薄壁类零件,在高速切削加工成形的过程中,产生的切削力和切削热对加工变形的影响较小,几乎可以忽略不计[8]。Zhang 等[9]研究了T 形薄壁件在不同厚向加工位置处的加工变形规律,认为适当的加工位置可以有效地降低零件变形。Huang 等[10]综合考虑了毛坯初始残余应力和切削应力,分析了整体结构件的加工变形规律,再通过化铣实验验证分析后认为,相比于切削应力,毛坯初始残余应力对加工变形的影响占到九成以上。该结果进一步表明了毛坯初始残余应力是零件加工变形的关键因素。张以都等[11]分析了不同走刀路径对加工变形的影响规律,认为若只考虑毛坯初始残余应力的情况下,走刀路径对工件变形的影响很小,可以忽略不计,也得出在高速加工中可以忽略切削力/切削热对加工变形的影响。上述这些研究方法,主要通过有限元仿真手段来实现。虽然能较为精确地计算出零件变形,但并没有进一步提出更为合适的方法来减小零件的加工变形。
在实际的数控加工过程中,工程技术人员经过多年的经验积累,认为毛坯开槽会对零件的加工变形产生影响,并通过在毛坯上开槽,实现减小零件变形的目的。但开槽的工艺参数,变形的影响机理,目前仍然缺乏有效的理论依据。马海营等[12]提出了开槽对毛坯内应力释放的有限元仿真方法,通过开槽的方式,破坏毛坯内部的应力平衡,改变毛坯变形。但开槽释放变形对零件加工变形的影响,并没有作进一步的分析与研究。
本文结合理论分析、有限元方法及实验测试手段,深入研究开槽法对整体结构件加工变形的影响机理及开槽方式优化方法的加工变形控制策略。
1 变形分析与验证
高速加工过程中,影响整体结构件加工变形的关键在于毛坯初始残余应力,可采用层剥法、裂纹柔度法、盲孔法等方法测量[8-9,13]。因此,控制毛坯初始残余应力的释放,对整体结构件变形有着至关重要的作用。
1.1 变形力学模型
随着高速加工过程中的材料去除,毛坯初始残余应力势必获得释放,毛坯内原来的应力自平衡受到破坏。残余应力势必重新分布至一个新的平衡状态,从而导致零件发生变形。
毛坯在去除材料之前的初始状态,其内部横向方向Y上的残余应力分力σY(z),以及轧制方向X上的残余应力分力σX(z),沿厚度方向Z呈平衡状态,如图1 所示。
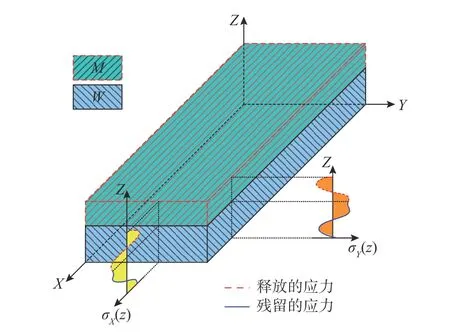
图1 去除材料区域示意图Fig. 1 Diagram of material removal region
随着材料M的去除,其内部的残余应力随之释放,造成零件W将受到如下的外载:
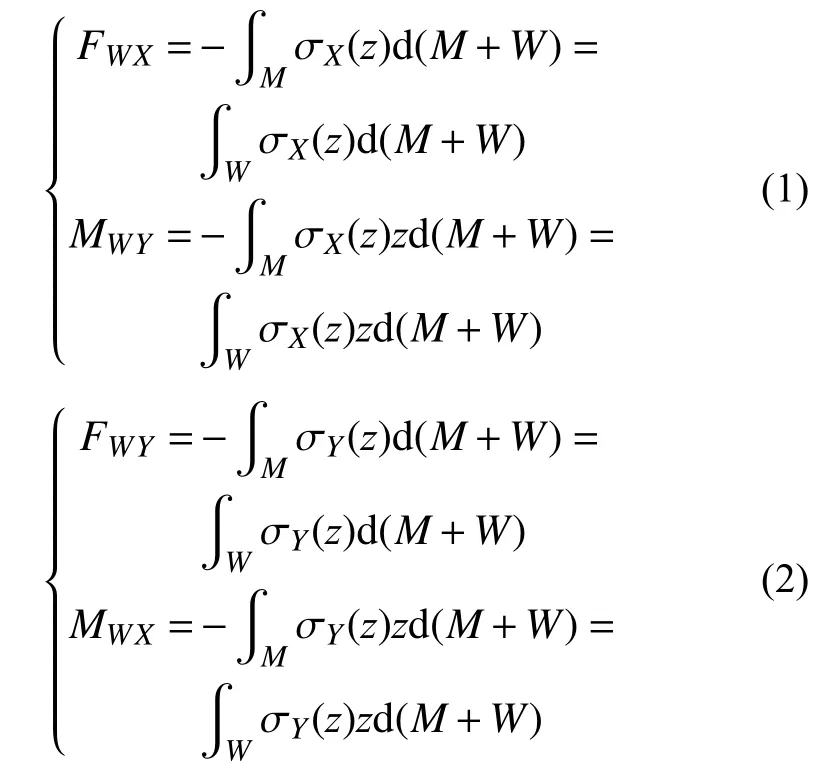
式中:FWX、FWY分别为材料M去除后零件W受到的轧制方向和横向方向的力;MWX、MWY分别为材料M去除后零件W受到的轧制方向和横向方向的力矩。
根据式(1)和式(2),可以将零件受到的外载进一步清晰地描述为:
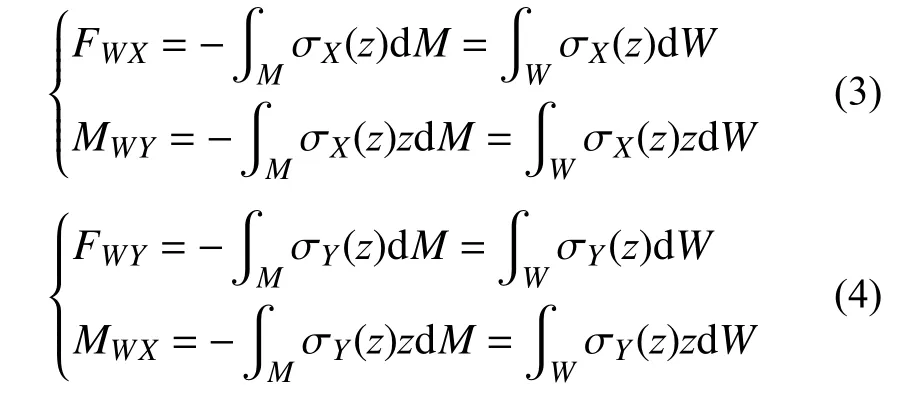
由式(3)和式(4)可以看出,零件W受到的载荷FWX、MWX和FWY、MWY,事实上就是零件内部的应力造成的。
在FWX、MWX和FWY、MWY作用下,零件W势必发生变形,使得其内部应力重新达到有个新的平衡状态。实际上,飞机整体结构件中梁类零件居多,假定其轴线方向为轧制方向X′,如图2所示,则其挠度可表示为:
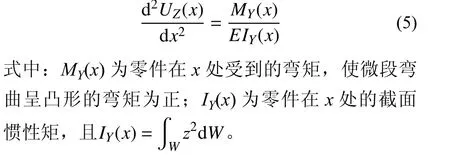

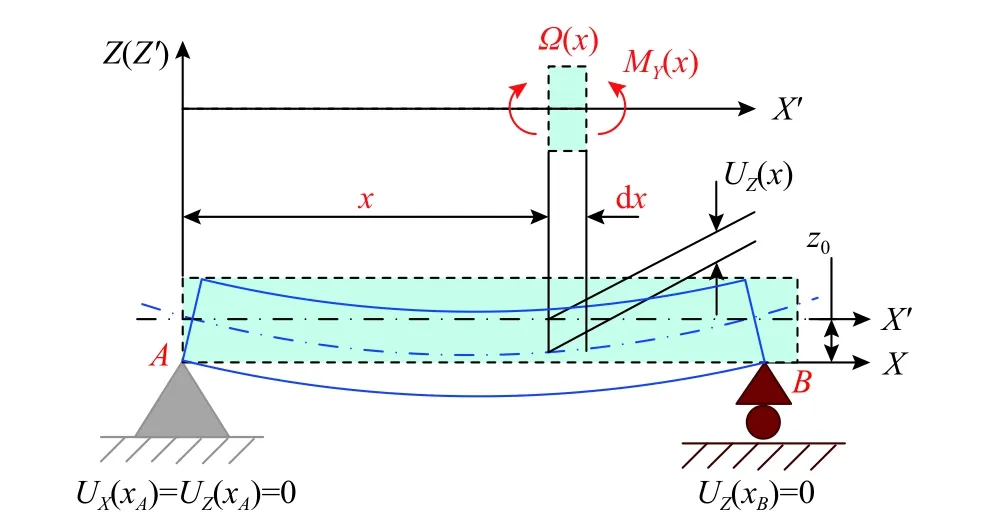
图2 零件变形示意图Fig. 2 Diagram of workpiece deformation
1.2 有限元分析方法
式(5)中的挠度UZ(x),可采用有限元方法进行计算。
1.2.1 薄板件
薄板件的材料选用弹性模量和泊松比分别为E=70.5 GPa、ν=0.33 的7075-T73 铝合金板材[8,14]。板材的尺寸为 200 mm × 20 mm × 6 mm,而零件的尺寸为200 mm × 20 mm × 4.5 mm,加工位置关系如图3 所示,其中阴影部分表示零件。
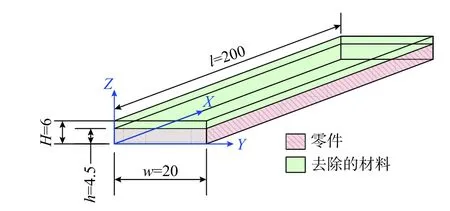
图3 零件与毛坯的关系Fig. 3 Relationship of workpiece and blank
毛坯的初始残余应力采用层剥法测得[8],由于横向方向的残余应力很小,可不予考虑,故其轧制方向的应力曲线如图4 所示。
沿厚度方向对薄板件进行均匀分层,共计划分40 层,每层厚度则为Δz=0.15 mm。这样,根据静力平衡方程,图4 的初始残余应力分布状态即可等效地离散为40 层的应力状态,每层的应力值如表1 所示。
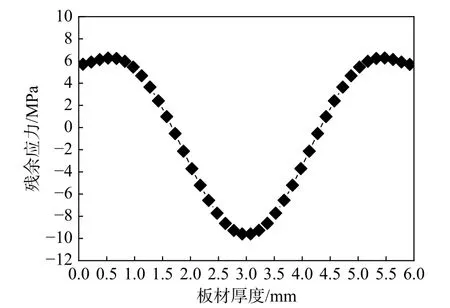
图4 薄板件的毛坯初始残余应力Fig. 4 Initial residual stresses of thin-plate workpiece
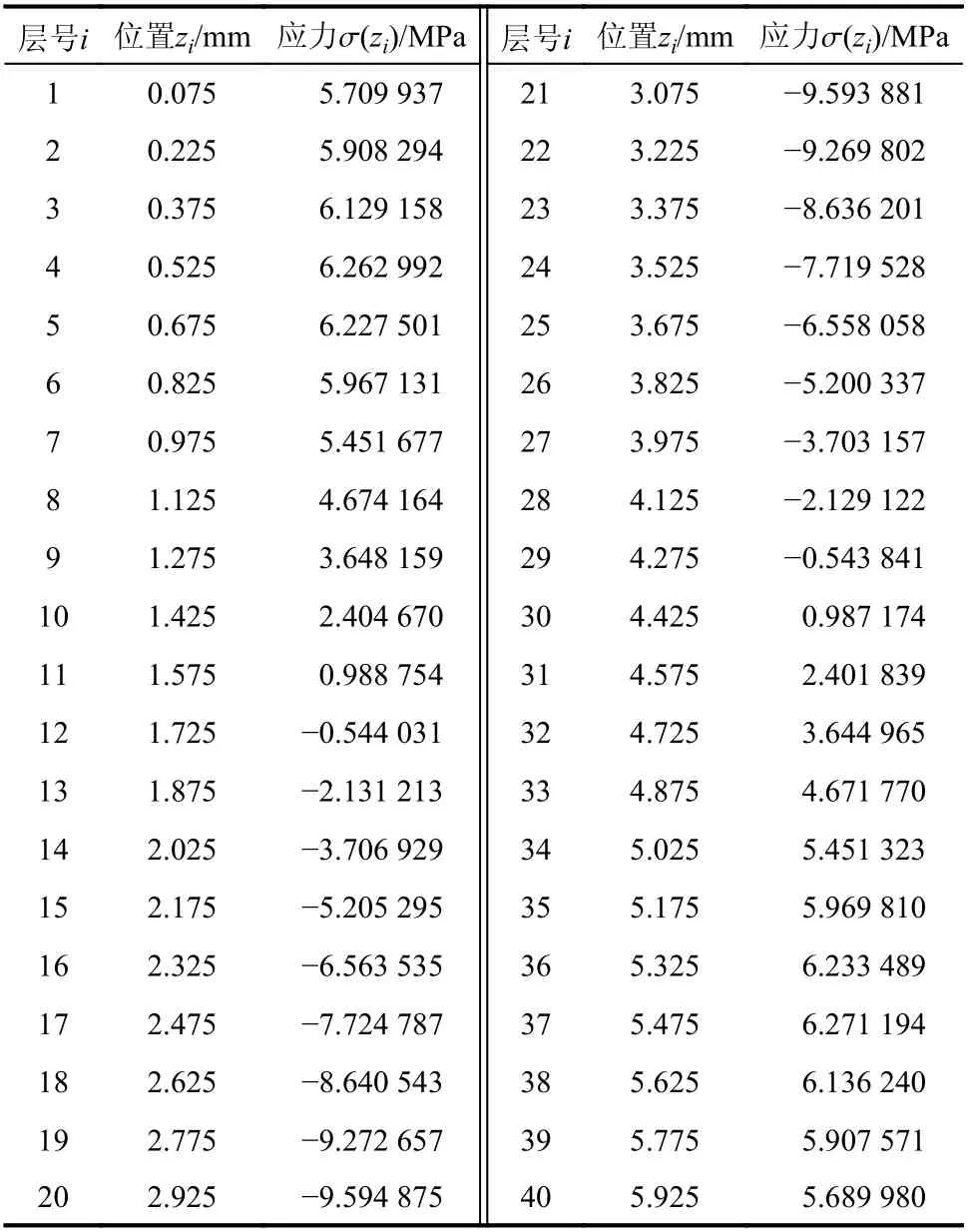
表1 薄板件毛坯每层残余应力值Table 1 Residual stresses in each layer of thin-plate workpiece
采用有限元软件ABAQUS 分析薄板件变形时,选用CPS4R 单元,设定网格密度为0.10,总共有114 000 个单元。由于薄板件仅受轧制方向应力作用,故施加表1 的应力后,采用“单元生死”技术模拟31 层~40 层的材料去除效应。再按照图2 所示的位移约束,经计算后可得有限仿真的变形云图,如图5 所示。
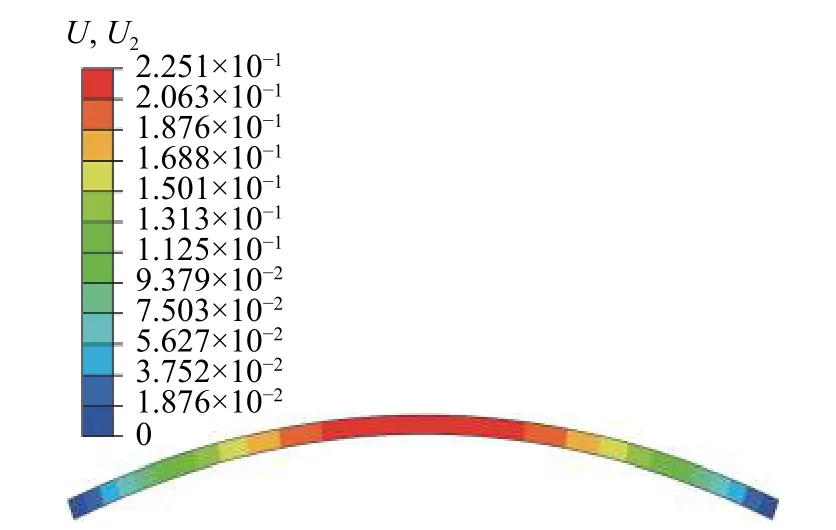
图5 薄板件变形的仿真结果Fig. 5 Simulated results of thin-plate deformations
由图3 可知,薄板件在任意位置x处的横截面均相同,容易获得薄板件的中性层高度和截面惯性矩分别为z0(x)=2.25 mm 和IY(x)=151.875mm4。这样,根据式(6)可知任意截面处的力矩可表示为:

实验过程包括以下3 个步骤,即材料去除、变形测量以及数据分析。考虑到高速铣削能够保证在动态加工过程中引入的残余应力水平较小,故选用法道加工中心VMC 3016L 上进行加工[8,14]。主轴转速设定为5000 r/min,装夹方案如图6(a)所示。变形测量在是同一台铣床上进行的,选用的测量探头如图6(b)所示。实验测量和有限元方法、挠度法求解得到的变形曲线比较如图7 所示,三者趋势非常吻合,尤其是有限元方法和挠度法的计算结果完全一致。在长度方向的100 mm 处,出现了最大变形,实验测量值为0.18 mm,有限元仿真值则为0.22 mm,两者的相对误差为22.22%。引起误差的主要原因是:一是薄板件加工引入了铣削应力;二是应变测量存在误差;三是变形测量存在测量误差。

图6 实验方案Fig. 6 Experiment scheme
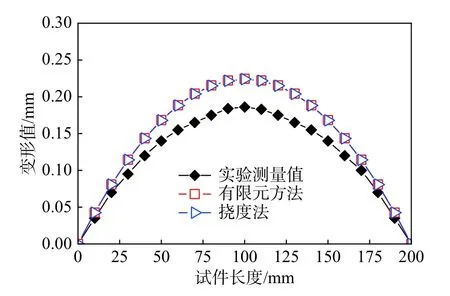
图7 挠曲变形对比Fig. 7 Comparison of deflection
1.2.2 三框结构件
要加工的零件为具有1100 mm× 80 mm×30 mm外廓尺寸的三框整体结构件[3,15]。三框件的腹板厚度为2 mm,而缘条壁厚仅为1.5 mm,如图8 所示。
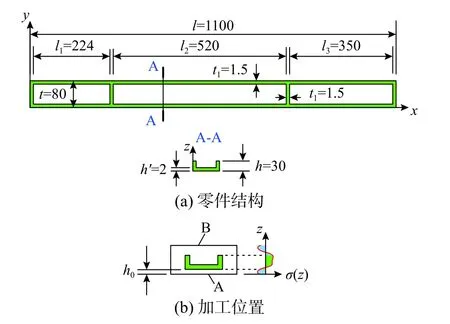
图8 三框整体结构件Fig. 8 Three-frame monolithic component
选用的毛坯材料为航空铝合金7050-T7451 预拉伸板材,外廓尺寸为1200 mm ×120 mm ×60 mm,弹性模量为E=71.7 GPa,泊松比为ν=0.33。
采用裂纹柔度法测得的毛坯初始残余应力分布曲线如图9 所示。沿着厚度方向对60 mm 厚的毛坯进行均匀分层,每层厚度设置为Δz=1.5 mm。这样,每层的应力可通过静力平衡方程获得,具体应力值如表2 所示。

表2 三框件毛坯每层残余应力值Table 2 Residual stresses in each layer of three-frame workpiece

图9 三框件的毛坯初始残余应力Fig. 9 Initial residual stresses of three-frame workpiece
若零件在毛坯中的加工位置为h0=16.5 mm,如图8(b)所示,采用单元类型为C3D20R 对零件进行网格划分,施加应力和约束后,有限元模型如图10(a)所示。计算所得的变形云图如图10(b)所示。
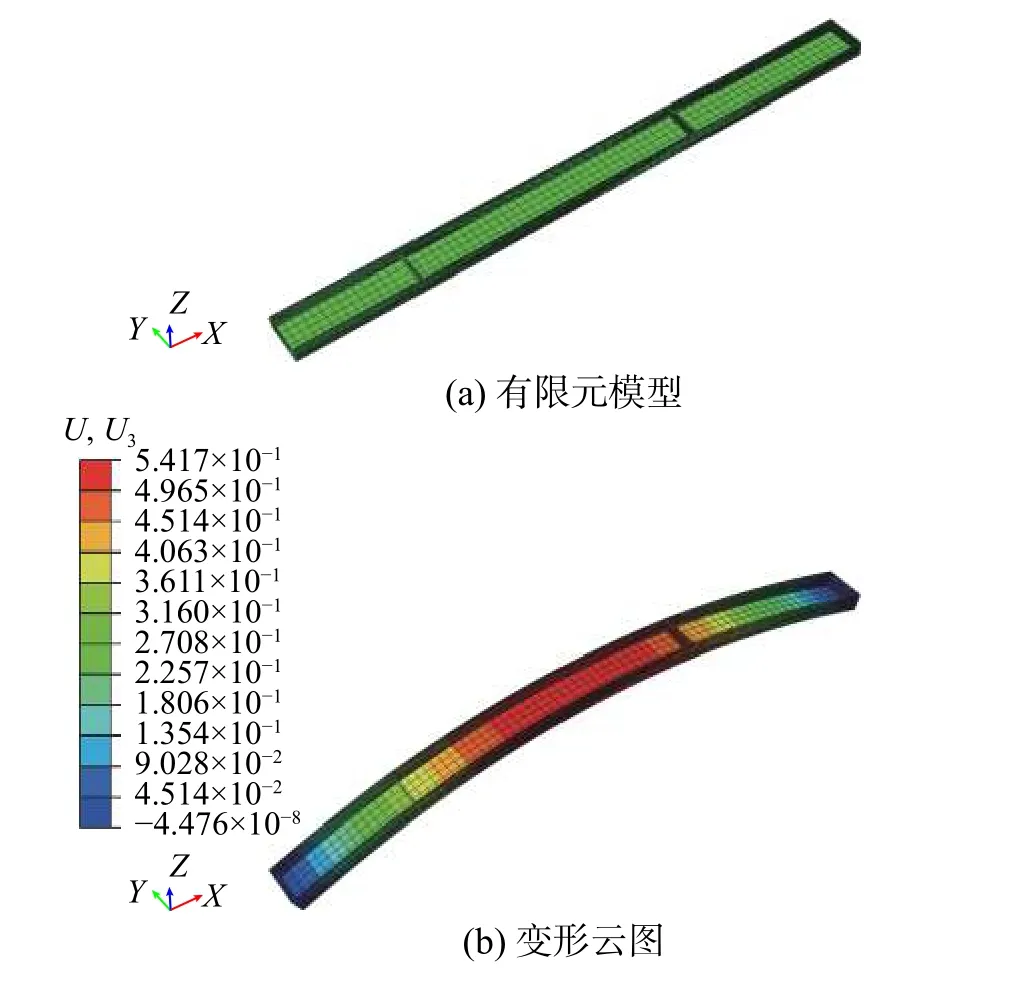
图10 加工位置为16.5 mm 的变形仿真Fig. 10 Deformation simulation of the machining position 16.5 mm
实验使用的材料是某主机厂提供的7050-T7451 美制铝厚板。整个实验加工过程分为以下3 个步骤:
第1 步:粗铣毛坯上下表面至加工位置
沿毛坯四周,采用压板顶住毛坯,对毛坯进行无应力装夹,如图11 所示。

图11 粗铣毛坯Fig. 11 Rough machining of blank
在高速铣床POWERMILL 9000×3000 上,按照表3 的加工顺序对毛坯进行铣面加工,加工余量逐渐减小,以保证零件的表面质量。并将毛坯下表面A 铣削至16.5 mm。采用同样的方式,亦可获得9.0 mm 的加工位置。

表3 加工位置的获取Table 3 Obtaining of machining position
第2 步:精铣零件至规定尺寸
采用压板沿毛坯上表面四周往下压紧后,三框件在高速加工中心K211A 3500×1500 上进行铣削加工。加工三个框的内腔时,为了提高铣削效率,选用直径为16 mm 的铣刀,而加工零件外侧缘条时,则采用直径为12 mm 的铣刀,主轴转速均设置为15 000 r/min。
其次,为了尽量避免铣削力和铣削热对加工变形的影响,在铣削外侧缘条时,轴向进给仅为0.5 mm。
此外,加工外缘条时,在三框件上留有0.2 mm的耳片,如图12(a)所示。再经钳工敲去耳片,取出零件,如图12(b)所示。

图12 加工后的三框件Fig. 12 Machined three-frame workpiece
第3 步:测量与分析变形数据

图13 为零件变形的实验测量结果与有限元仿真值的比较,测量腹板内中线关于长度方向的变形是近似光滑的曲线,因此实验测量和有限元仿真均采用腹板内中线的位置得到变形值。从图中可以看出,无论是16.5 mm 的加工位置还是9.0 mm的加工位置,其最大变形都在轧制方向的中间位置处,而且均具有较好的吻合度。加工位置16.5 mm时误差在10%之内,而加工位置9.0 mm 时误差在15%以内,这是因为加工位置9.0 mm 的变形量本身较小,仅有0.32 mm 左右。

图13 三框件的变形比较Fig. 13 Deformation comparison of three-frame workpiece
更为重要的是,从毛坯上去除的材料不同,导致释放的应力不同,最终造成零件变形也不一样。
2 应力释放对零件变形的影响规律
正如前面所述,从毛坯上去除材料后,残余应力获得释放,毛坯将产生变形,这里称为毛坯释放变形。显然,在产生变形的毛坯中加工零件,由于再一次释放应力,造成零件的最终变形。
这里,假定通过开一通槽去除厚度为d的材料(属于特殊的通槽,即槽深dmm,槽宽b=20 mm)来释放应力,这里d<1.5 mm。采用有限元方法来研究毛坯释放变形与零件变形之间的关系。
根据槽和零件的形状对毛坯进行切割,然后采用C3D20R 单元对毛坯进行均匀分层划分网格,每层的厚度为1.5 mm,单元密度为15 mm,如图14 所示。
网格划分后,依据每层的网格、槽、零件成形时要去除的材料分别定义为一个单独的层节点集合、槽节点集合和材料节点集合。将表1 的残余应力施加到对应的层上,类似于图2 施加约束,采用“单元生死”技术模拟开槽效应,如图14(b)所示。计算毛坯释放变形和相应的应力,如图14(c)所示。

图14 有限元操作流程示意图Fig. 14 Schematic diagram of finite element operation flow
导入模型及其相应数据后,移动释放变形后的节点至待加工表面处,如图14(d)所示。选用材料节点集合,继续利用“单元生死”技术模拟零件的加工过程,施加位置约束条件后计算可获得有限元结果,如图14(e)所示。
根据上述有限元分析方法,若6 mm 厚的毛坯初始残余应力为对称分布(见图4),在此毛坯顶部进行开槽(铣去一个平面)释放变形,然后再进行零件加工(其加工位置见图3)。这里以点(100 mm,10 mm, 0)为观测点来分析毛坯释放变形和零件加工变形的演变规律,如表4 和图15 所示。
由图15 可知,当开槽深度d由0 增至1 mm时,毛坯释放变形由0 增加到0.1217 mm,但零件的加工变形却由0.2251 mm 减小至0.0987 mm。由此可见,随着毛坯释放的变形越来越大,零件的加工变形越来越小。
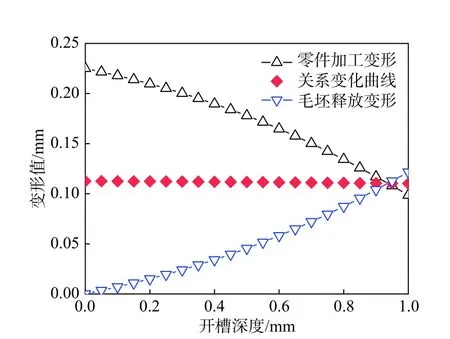
图15 零件加工变形与毛坯释放变形的关系Fig. 15 Relationship between the workpiece machining deformation and the blank releasing deformation
此外,由表4 可知,毛坯释放变形和零件加工变形这两条曲线几乎关于直线y=0.1116 对称,仅在1%左右波动。由此可见,毛坯释放多大变形,零件加工就能减小多大变形。
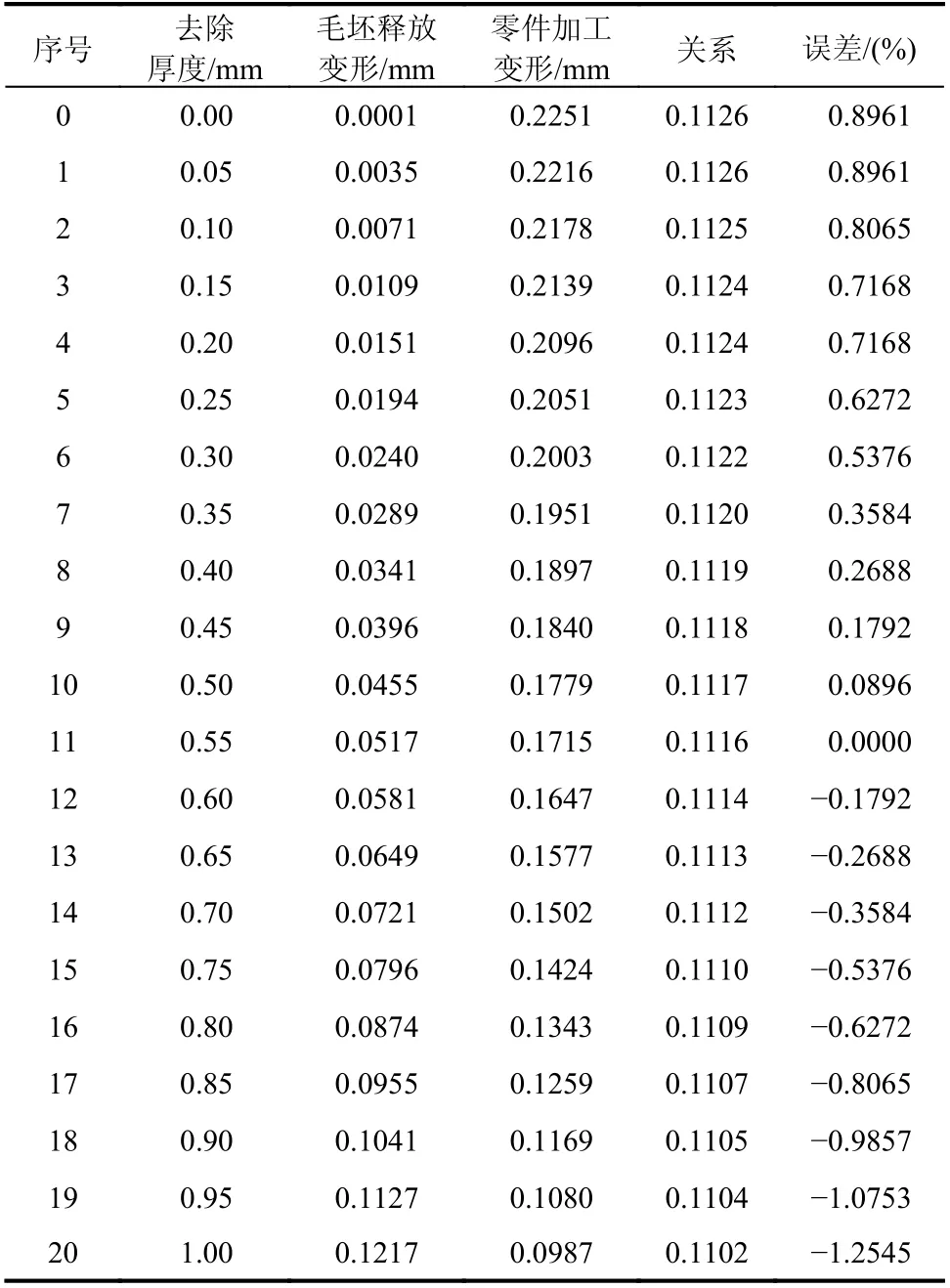
表4 零件加工变形与毛坯释放变形之间的关系Table 4 Relationship between the workpiece machining deformation and the blank releasing deformation
特别地,假定在开槽前,计算出了零件的加工变形。那么在开槽时使得毛坯释放出和零件加工变形一样的变形,则零件的最终加工变形应为零。
3 开槽方式对变形的影响规律
显然,开槽的方向、位置w、槽宽b、槽深d的不同,不仅毛坯的抗弯模量不同,释放的应力也会不同,因而释放的毛坯变形就不相同,进而对零件加工变形的影响自然也会产生不一样的效果。
3.1 开槽方位
这里,以图8(a)的三框结构件加工为例,研究单槽开槽方式中毛坯释放变形和零件加工变形的演变机制。
巩俐是那种知道自己想要什么,就全力以赴去争取的人,虽然是女儿身,但她一身骨气,只要认定的事情,就算撞的头破血流,也会坚持到底。相比接连失败的艺考之路,巩俐的出道之路则比较顺利,第一部戏就遇到了当时国内比较热的导演张艺谋。
开槽位置主要有轧制方向开槽与横向方向开槽两种,如图16 所示。假定零件在毛坯中的加工位置为h0=9 mm,这时在毛坯上表面上分别开一个10 mm×10 mm(即槽宽b=10 mm,槽深d=10 mm)和10 mm×16 mm(即槽宽b=10 mm,槽深d=16 mm)的通槽,选取零件下表面的中点,即坐标为(600 mm,9 mm, 60 mm)的点,作为观测点来揭示开槽方位对变形的影响规律,如图17 所示。
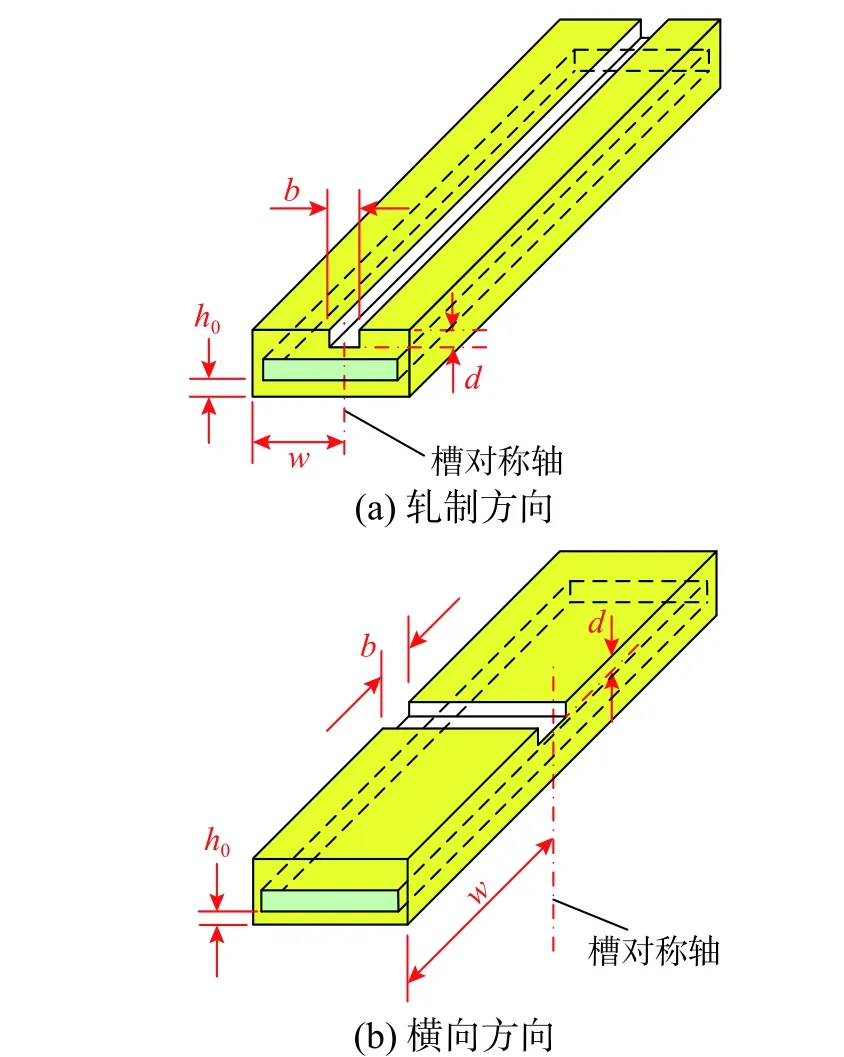
图16 通槽位置示意图Fig. 16 Position of through slot
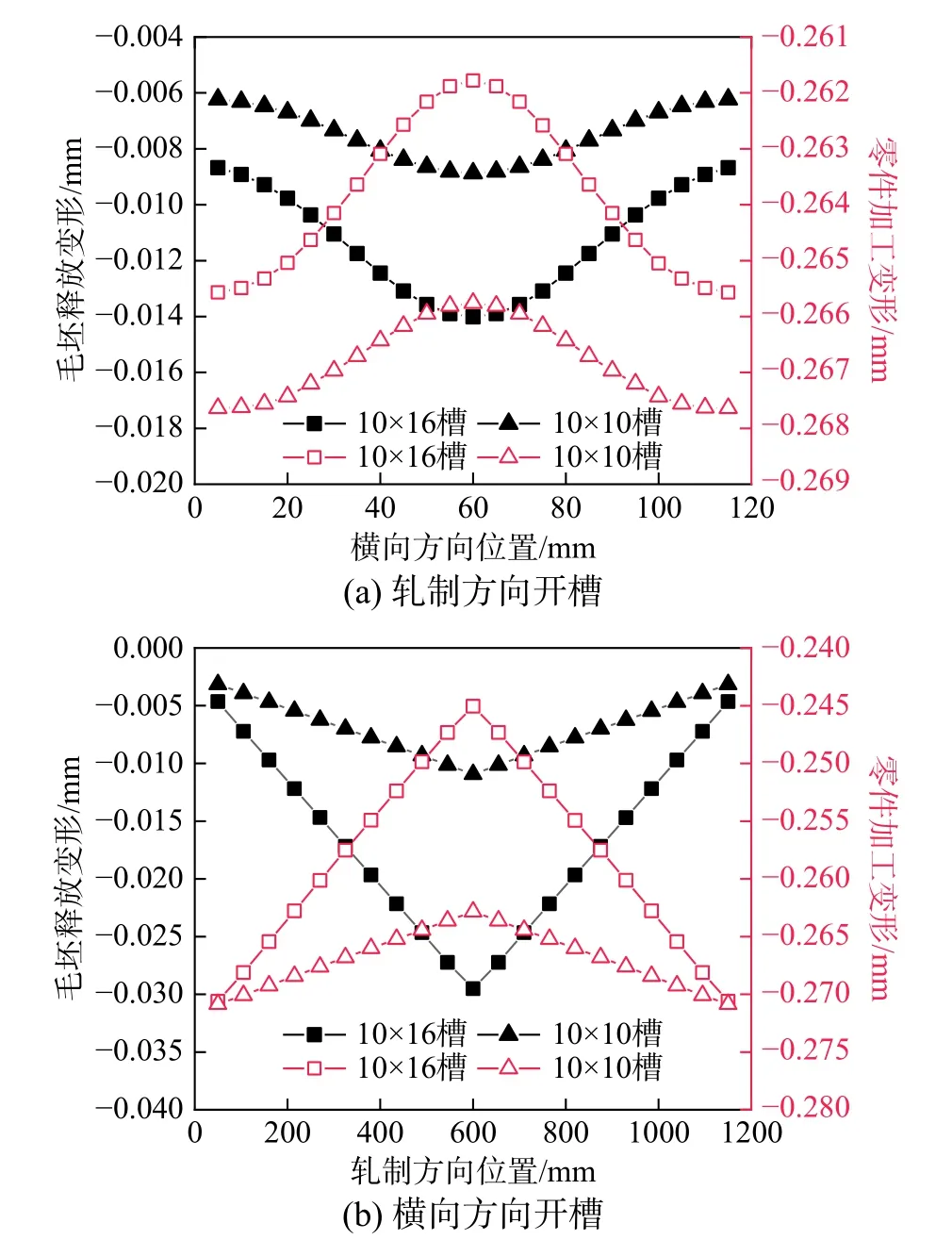
图17 开槽方位的影响Fig. 17 Influence of slotting direction
由此可见,沿轧制方向分别开一个10 mm ×10 mm、10 mm × 16 mm 的通槽时,若槽开在横向方向位置w=60 mm 处,毛坯释放最大变形分别为-0.008 87 mm、-0.014 01 mm,零件最小加工变形分别为-0.265 76 mm、-0.261 78 mm。
而沿横向方向分别开一个10 mm×10 mm、10 mm×16 mm 的通槽时,则槽开在轧制方向位置w=600 mm 处,毛坯释放最大变形分别为-0.010 93 mm、-0.029 51 mm,零件最小加工变形分别为-0.262 84 mm、-0.245 05 mm。
由此可见,无论是沿轧制方向还是沿横向方向开槽,都是在板材的中心处能释放最大的毛坯变形,此时零件加工变形也最小。但横向方向开槽的变形控制效果好于轧制方向开槽的变形控制效果。
3.2 开槽槽宽
由于在横向方向上的中心位置处开槽零件变形最小,故考虑在此处开不同的槽,这里假定槽深为d=10 mm,而槽宽b的取值范围为0 mm~1150 mm。
如果零件在毛坯中的加工位置为h0=9 mm,则依然选择零件下表面上的中心点(600 mm,9 mm, 60 mm)为观测点。这样,随着槽宽的改变,零件加工变形和毛坯释放变形的变化规律就能利用第2 节介绍的计算方法获得,如图18 所示。
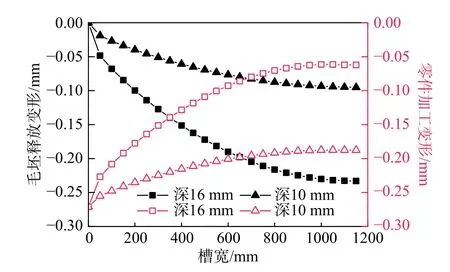
图18 开槽槽宽的影响Fig. 18 Influence of slot width
通过对比分析可知,在槽深一定的情况下,槽宽越大,毛坯释放变形越大,零件加工变形则越小。
3.3 开槽槽深
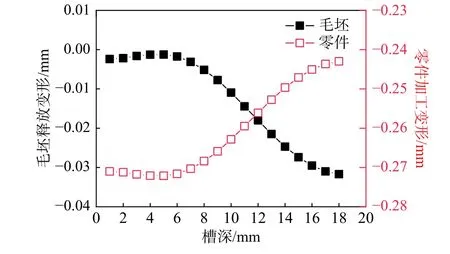
图19 开槽槽深的影响Fig. 19 Influence of slot depth
由此可以看出,槽深和工件变形之间并非单一的线性关系,存在极值点,而造成槽深这种变形趋势的主要原因在于当量残余应力的数值和中性层高度的变化。因此,控制好槽深的大小,即可改变毛坯变形。
4 零件变形的控制方法
综上所述,零件变形随着开槽方式的不同而不同,而开槽方式涉及朝向、位置、槽深、槽宽等多个几何参数,为了更好地控制零件加工变形,可通过优化开槽方式使得加工变形最小。
4.1 训练样本的确定
由于开槽的参数较多,利用有限元方法仿真计算加工变形效率较低,故采用神经网络来实现加工变形的预测。
由于横向开槽比轧制方向开槽效果更好,故开槽方向选择为横向方向。这样,开槽几何参数就减少为槽深x1、槽宽x2、以及位置x3等三个因素,假定其取值范围分别为1 mm≤x1≤15 mm、10 mm≤x2≤ 200 mm、300 mm≤x3≤950 mm。
为了保证神经网络的预测精度,需要有足够的开槽几何参数用于训练,这里采用正交试验设计方法来收集用于训练的单槽参数。由于开槽参数只有槽深、槽宽、位置等三个因素,为此应建立两个正交表获得更多组数据作为神经网络的训练参数,如表5 所示。

表5 正交表Table 5 Orthogonal table
表5 为两张八水平三因素的正交表,每张对应64 组输入样本,共计128 组数据。
利用第2 节的有限元方法,计算出每组输入样本对应的毛坯释放变形(或零件加工变形)δ,作为网络的训练样本,如附表A 所示。
4.2 预测模型
BP 人工神经网络是一种多层前馈神经网络,主要特点是信号向前传递,误差反向传递。从简单实用的角度出发,一个具有n个隐藏层的多层前馈型网络可以逼近任何多变量函数。综合考虑网络的学习速度和泛化能力,以及可能会出现的过拟合问题,隐藏层神经元个数不宜过多,故最终将BP 神经网络结构设置为3-7-1 结构[16-17],即输入层3 个神经元,隐藏层分别为7 个神经元,输出层1 个神经元,如图20 所示。

图20 网络net 结构Fig. 20 Structure of network net
获取输入和输出变量之后,为了避免各维数据之间的数量级差别过大而造成的网络计算误差,需要对输入输出量进行数据归一化处理,把数据转化为[0, 1]之间的数。归一化的方法主要有最大最小法和平均数方差法,这里采用第一种方法,即:
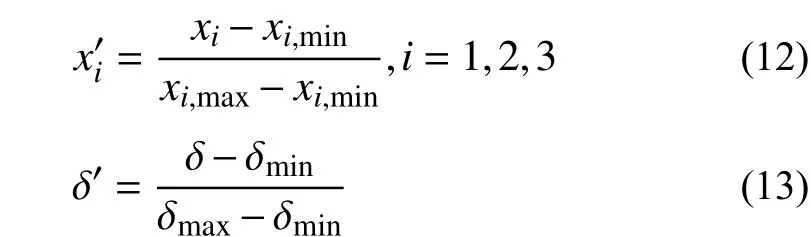
式中:xi,min、δmin为相应样本的最小值;xi,max、δmax为相应样本的最大值。
样本归一化后,就可进行网络训练,训练参数的设定如表6 所示。隐藏层神经元、输出层神经元传递函数分别采用S 型正切函数tansig、S 型对数函数logsig。网络的训练函数则选用trainlm。

表6 神经网络训练参数Table 6 Training parameters of neural network
根据附表A 的数据,利用MATLAB 的sim 函数对上述建立的网络进行训练。图21(a)网络训练过程,仅迭代计算了77 步就收敛了,而图21(b)为网络预测值与其对应的仿真试验值之间的比较,表明训练出的网络具有较高的吻合度,而测试样本点(数据见附表B)与试验值之间存在着小范围的偏离,其预测误差最大误差为4.8964%,最小误差为0.2511%。这样,可得毛坯释放变形的网络预测模型为:

图21 网络训练与测试Fig. 21 Training and testing of network net

式中:net 为BP 网络;sim 为网络仿真函数;x=[x1,x2,x3]T为输入样本。
4.3 优化方法
为了获得最小的零件加工变形,势必在开槽过程中使得毛坯释放的变形最大。为此,在建立神经网络预测模型的基础上,开槽方式的优化模型可进一步提出如下:
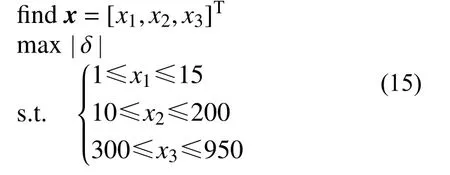
由式(14)和式(15)可知,槽的参数x1、x2、x3与目标函数δ 之间关系复杂,梯度信息难以获得。而且,与经典非线性问题大多采用的梯度下降法相比,遗传算法的全局搜索能力更强。因此,采用遗传算法来解算式(15)。
遗传算法进行搜索之前,采用二进制编码方法先将解空间的数据x1、x2、x3编码为长度为30 的染色体U(即遗传空间的基因串结构)。
然后随机产生N=50 个初始串结构数据,每个串结构数据称为一个个体Uk(1≤k≤N),N个个体构成了一个种群。染色体Uk中第一个10 位代表槽深x1的取值,第二个10 位代表槽宽x2的取值,第三个10 位代表位置x3取值。遗传代数MAXGEN=200。
适应度函数是用来判断种群中个体的好坏,是进行自然选择的唯一依据。一般情况下,适应度越大的染色体越健壮,在下一代的生成概率越大;适应度越小的染色体越虚弱,在下一代的生成概率越小,越容易淘汰。故适应度函数可定义为:

根据图22 所示的遗传算法对槽深x1、槽宽x2、位置x3进行优化,优化过程如图23 所示。经过81 次迭代,遗传算法达到收敛,观测点(600 mm,9 mm, 60 mm)处的目标函数值max{|δ|} = 0.0956 mm,此时毛坯释放的最大变形为δmax= -0.0956 mm。相应的开槽参数分别为槽深x1=15 mm,槽宽x2=200 mm,位置x3=599.2229 mm。也就是说,在毛坯横向方向的中心位置处开槽,槽深、槽宽均开到最大,释放的毛坯变形最大。

图22 遗传算法求解流程Fig. 22 Solving flowchart of genetic algorithm
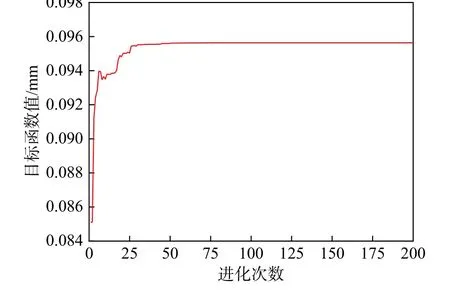
图23 遗传算法求解过程Fig. 23 Solving process of genetic algorithm
将槽深x1=15 mm、槽宽x2=200 mm、位置x3= 599.2229 mm 这组开槽参数用于零件加工仿真分析,可得观测点(600 mm, 9 mm, 60 mm)处的毛坯释放变形、零件加工变形分别为-0.0998 mm、-0.1775 mm。与毛坯释放变形的预测结果-0.0956 mm相比,预测误差仅为4.1971%,预测结果和仿真值非常吻合。
而在毛坯没有开槽释放变形的情况下,此时零件的加工变形云图,如图24 所示。由此可见,观测点(600 mm, 9 mm, 60 mm)处的变形值为-0.270 95 mm。与最优开槽方式的结果比较可知,零件的加工变形减小了0.093 44 mm。结果表明:开槽释放变形对加工变形的控制效果比较明显,在最佳开槽方式下,零件加工变形减小了34.5%。
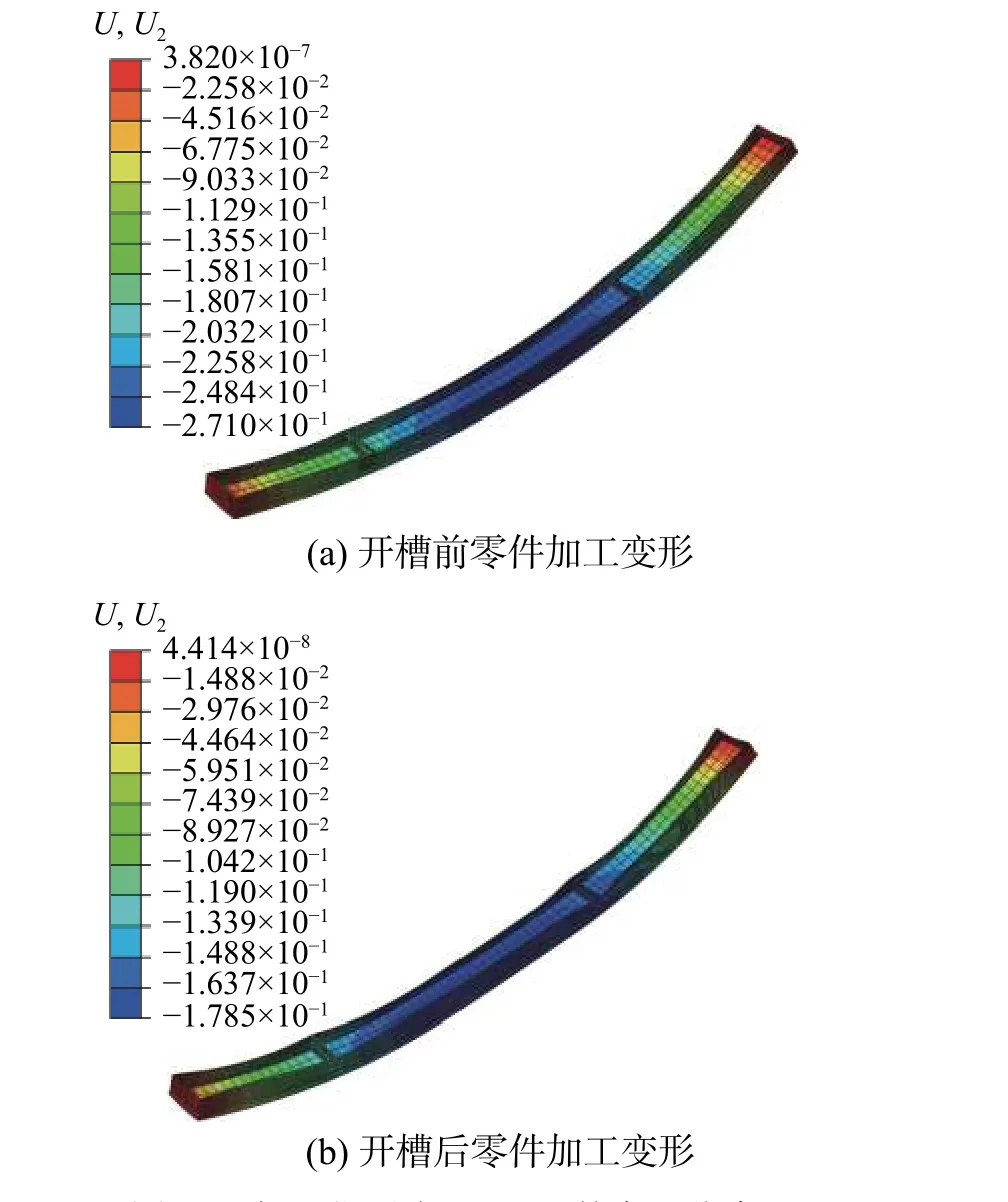
图24 加工位置为9.0 mm 的变形仿真Fig. 24 Deformation simulaition of the machining position 9.0 mm
5 结论
从毛坯开槽释放应力的角度出发,揭示了不同开槽方式下毛坯释放变形与零件加工变形之间的关系,提出了毛坯开槽的“有限元分析-神经网络预测-遗传算法优化”的零件加工变形控制方法,具体研究内容具体如下:
(1)建立了零件加工变形的挠度解析模型及其相应的有限元仿真方法。零件加工变形的挠度计算值、有限元仿真值在变形趋势和变形量方面均较为吻合。基于此,利用有限元方法揭示了毛坯释放变形与零件加工变形之间的规律,并能为神经网络准确计算输入样本。
(2)在利用正交试验设计方法选定128 组代表性样本的基础上,建立了毛坯释放变形的神经网络预测模型。网络测试集表明,网络预测模型的预测误差不超过5%。显见,所建立的神经网络预测模型可以准确地描述槽深、槽宽、开槽位置与毛坯释放变形之间的关系。
(3)通过嵌入毛坯释放变形地神经网络预测模型,提出了开槽方式的优化模型及其遗传算法的解算方法。单槽开槽方式的优化结果表明,与不开槽释放应力相比,毛坯在最佳开槽方式下,零件加工变形减小了34.5%。由此可知,在毛坯上开单个通槽,沿横向方向开槽的加工变形小于沿轧制方向开槽,且在中间位置的开槽效果最好;此外,槽深、槽宽开得越大,毛坯释放变形越大,零件加工变形则越小。
附录A: 训练样本
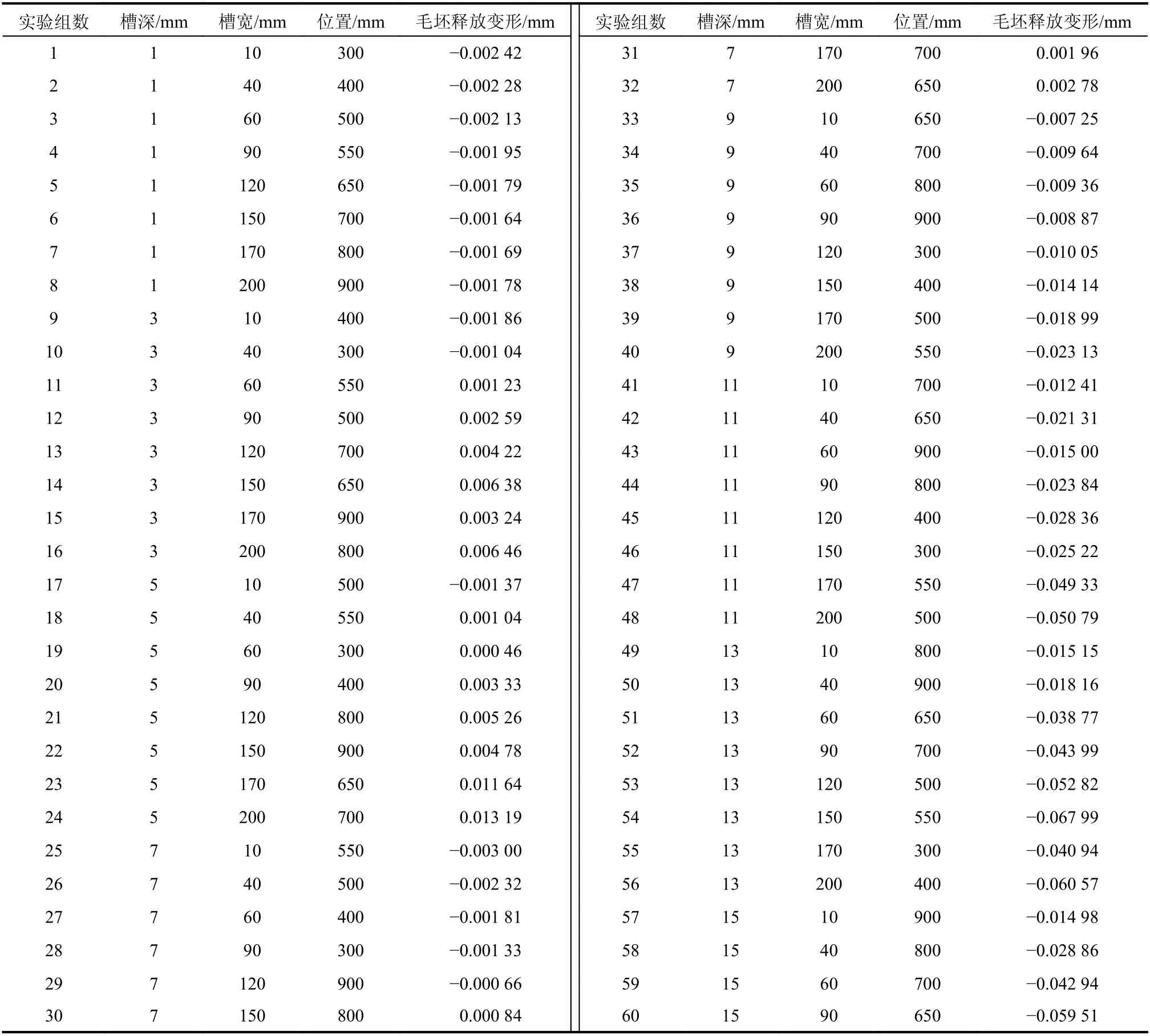
附表A 神经网络的训练样本Attached table A Training samples of neural network
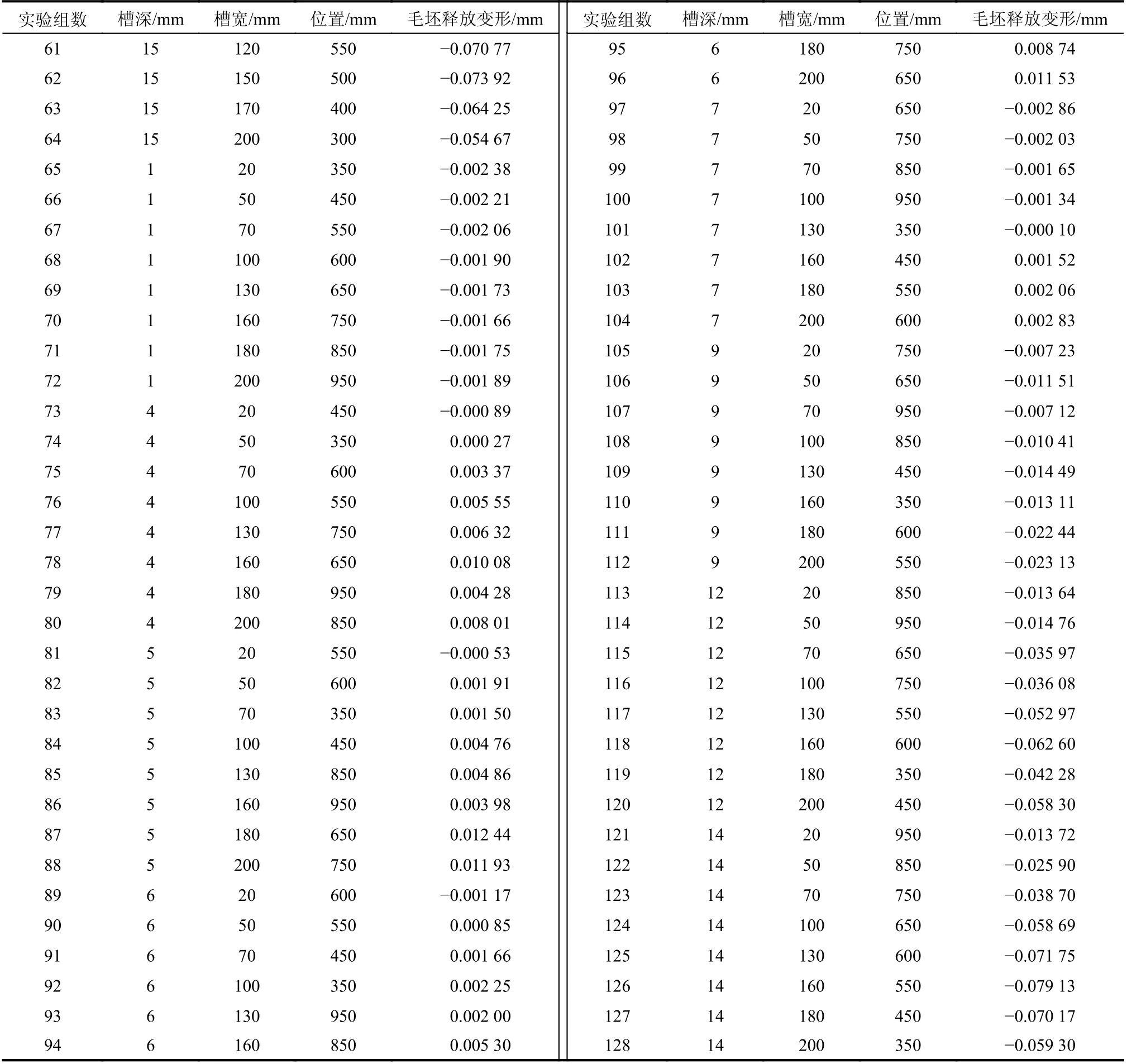
续附表A
附录B: 测试集
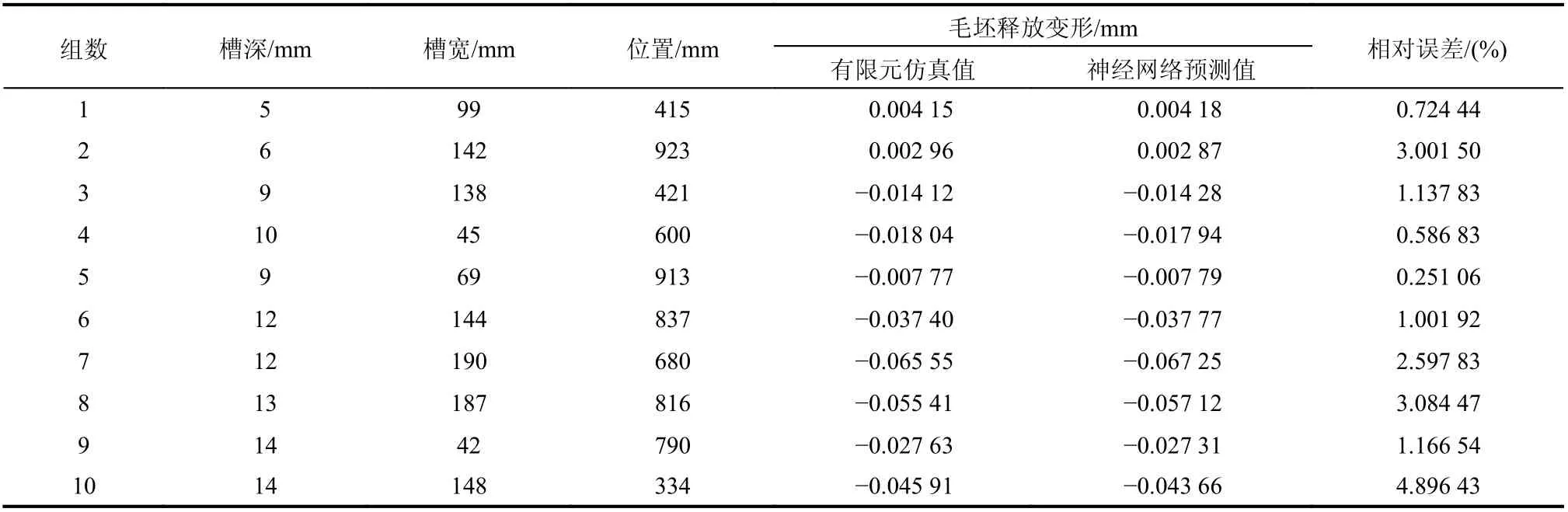
附表B 神经网络测试集Attached table B Test set of neural network
