基于三维能量屈服准则的新老混凝土无锚筋结合面抗剪强度统一计算方法

林拥军，徐文强，杨敏润，奉 鑫，余国菲

(西南交通大学土木工程学院，成都 610031)

新老混凝土结合面的黏结抗剪与抗拉性能是衡量既有钢筋混凝土构件加固成功与否的关键，而黏结抗剪性能尤为重要[1-5]。新老混凝土结合面分为有锚筋结合面和无锚筋结合面两种形式。无锚筋结合面是新混凝土、老混凝土及界面材料的组合体，已有研究表明，结合面是构件的薄弱部位，在剪切荷载作用下，构件会因新老混凝土无锚筋结合面开裂、两侧产生错动而破坏[6]。新老混凝土无锚筋结合面的抗剪强度与老混凝土表面粗糙度、结合面正应力、新(老)混凝土强度及界面材料等因素有关，国内外学者提出了一些计算方法[7-9]，这些方法可分为考虑正应力和未考虑正应力2 类，能够考虑正应力以及正应力为0 的统一计算公式还未见报道。

考虑正应力的计算方法相对较少，主要有：袁群等[10]基于Mises 屈服条件和Mohr-Coulomb破坏准则，采用塑性极限上限定理所推导的新老混凝土结合面抗剪强度解析计算式，由于混凝土是压硬性摩擦材料，不仅具有黏聚力还具有摩擦力，而Mises 屈服条件比较适用于金属材料，并不适合于混凝土[11-14]，导致该方法存在计算值与试验值偏差较大的问题；刘健[15]在新老混凝土结合面压(拉)剪复合受力抗剪试验基础上，采用统计分析和数据拟合方法，得到压(拉)剪复合受力抗剪强度计算公式，该方法理论依据较为缺乏且适用范围受限。相较于考虑正应力的计算方法，不考虑正应力的计算方法较多，主要有：王振领[16]根据新老混凝土结合面剪切试验，提出考虑结合面粗糙度、界面剂类型及新老混凝土立方体抗压强度平均值等参数的抗剪强度计算公式；郭进军[17]根据新老混凝土结合面剪切试验数据，以相对抗剪强度作为控制参数，采用最小二乘法拟合得到的结合面抗剪强度计算公式；黄璐等[18]以剪切试验数据为基础，采用多元回归分析得到的新老混凝土结合面抗剪强度改进计算式；Gohnert[19]根据预制与现浇混凝土结合面剪切试验数据，提出的用于评估预制与现浇混凝土，计算结果与结合面粗糙度呈线性关系的结合面抗剪强度计算公式；Santos 和Júlio[20]提出的基于黏聚力安全系数的计算公式。

总的来说，无论是考虑正应力的计算方法，还是未考虑正应力的计算方法，大都是以剪切试验结果为基础，进行数据拟合得到的，这些方法除理论依据较为缺乏、应用范围受到限制外，计算精度也有待提高。

鉴于混凝土的压硬性岩土类摩擦材料特点，郑颖人等[21-24]基于对材料屈服条件和破坏条件的塑性分析，建立了适用于混凝土材料的三维能量屈服准则。为此，本文根据新老混凝土无锚筋结合面破坏特征、机理，分析其剪切破坏机构，并假定混凝土为体积不可压缩的刚塑性材料，基于混凝土材料的三维能量屈服准则、虚功原理和塑性极限理论，详细推导了新老混凝土无锚筋结合面的抗剪强度理论计算公式，引入考虑正应力和粗糙度的综合影响系数，对理论公式进行修正，得到新老混凝土无锚筋结合面抗剪强度统一计算方法。与已有计算方法及试验结果的对比分析表明，所提出的统一计算方法可用于压(拉)剪复合受力构件和纯剪受力构件无锚筋结合面的抗剪强度计算，计算精度优于已有计算方法。

1 基于三维能量屈服准则的塑性极限分析

1.1 破坏机构与假定

已有剪切试验结果表明，无锚筋新老混凝土结合构件的破坏位置多集中于新老混凝土交界面，其剪切破坏机构可表示为图1[10,25-26]。该破坏机构由老混凝土刚性体、老混凝土塑性体Vo、新混凝土刚性体、新混凝土塑性体Vn及新老混凝土结合面 5 部分组成。图中：h为结合面高度；δ 为老(或新)混凝土塑性微元体厚度；Q为极限剪切荷载。以老混凝土刚体部分为参考体，其速度为0，新混凝土刚体部分速度为v*，新混凝土刚体部分的运动会传递至新、老混凝土塑性体，由于塑性作用，二者的速度会折减。

图1 新老混凝土无锚筋结合面剪切破坏机构Fig. 1 Shear debonding model of new-to-old concrete without anchor bars

根据虚功原理和塑性极限理论，该破坏机构还应遵循以下假定：

1) 混凝土为理想刚塑性材料，具有体积不可压缩性，并具有压硬性[14]。

2) 极限剪切荷载作用时，假定靠近新老混凝土结合面处的新混凝土和老混凝土微元体处于塑性状态。

3) 新老混凝土结合面是新混凝土塑性体和老混凝土塑性体的交界面，为速度间断面，其厚度可近似看作0。

6) 所产生的变形很小。

1.2 基于三维能量屈服准则的加载函数

混凝土为岩土类材料，具有压硬性，三向压力作用下，其强度、黏聚力均会提高，莫尔应力圆也会相应的增大。为在屈服条件中考虑这种特性，高红等[22]从能量角度对岩土类材料在剪切受力状态下的屈服特性进行研究，提出了考虑材料压硬性的三维能量屈服准则：

1.3 新老混凝土塑性体内力虚功

根据Drucker 塑性公设，塑性功具有不可逆的性质，即[24]：

1.4 速度间断面内力虚功

2 新老混凝土无锚筋结合面抗剪强度统一计算方法

2.1 抗剪强度理论计算公式

2.2 抗剪强度统一计算方法

根据表1 中不同强度等级混凝土的抗剪切强度值，进行曲线拟合后，可得到混凝土抗剪切强度的计算公式如下：

表1 不同强度等级混凝土的黏聚力c 、内摩擦角 φ、抗剪强度 τY 及α 系数取值Table 1 Cohesion c, internal friction angle φ, shear strength τY, and α coefficient values of different strength concrete

式中，fcu,k为混凝土立方体抗压强度标准值。

鉴于实际结构往往处于拉、压、剪复杂的受力状态，引入考虑正应力和粗糙度的综合影响系数，基于已有剪切试验数据并借助三维曲线拟合技术，对抗剪强度理论计算公式进行修正后得到无锚筋结合面抗剪强度统一计算公式如下：

3 计算方法的试验验证

为验证本文提出的新老混凝土无锚筋结合面抗剪强度统一计算公式的有效性，在归纳总结已有新老混凝土无锚筋结合面抗剪强度计算方法的基础上，基于已有新老混凝土压(拉)剪试验和新老混凝土纯剪试验数据(注：前述进行曲线拟合的试验数据不再用于对计算方法的验证)，将本文方法计算值、已有方法计算值与试验结果进行对比分析。

3.1 已有计算方法简介

如前所述，已有关于新老混凝土无锚筋结合面抗剪强度计算方法可分为考虑正应力(方法1～方法2)和不考虑正应力(方法3～方法7) 2 类，其具体计算表达式详见表2。

表2 已有新老混凝土无锚筋结合面抗剪强度计算公式Table 2 Formulas for calculating the shear strength of the existing new-to-old concrete interface without anchor bars

3.2 与已有方法、试验结果的对比

3.2.1 压(拉)剪复合受力试验试件

为了解本文方法对于计算新老混凝土无锚筋结合面压(拉)剪复合受力试件抗剪强度的有效性，分别采用本文方法、考虑正应力的方法1 和方法2 对文献[15]中的27 个新老混凝土压(拉)剪复合受力试验试件的抗剪强度进行计算。压(拉)剪试件参数、试验值、不同方法的计算值及偏差率见表3。

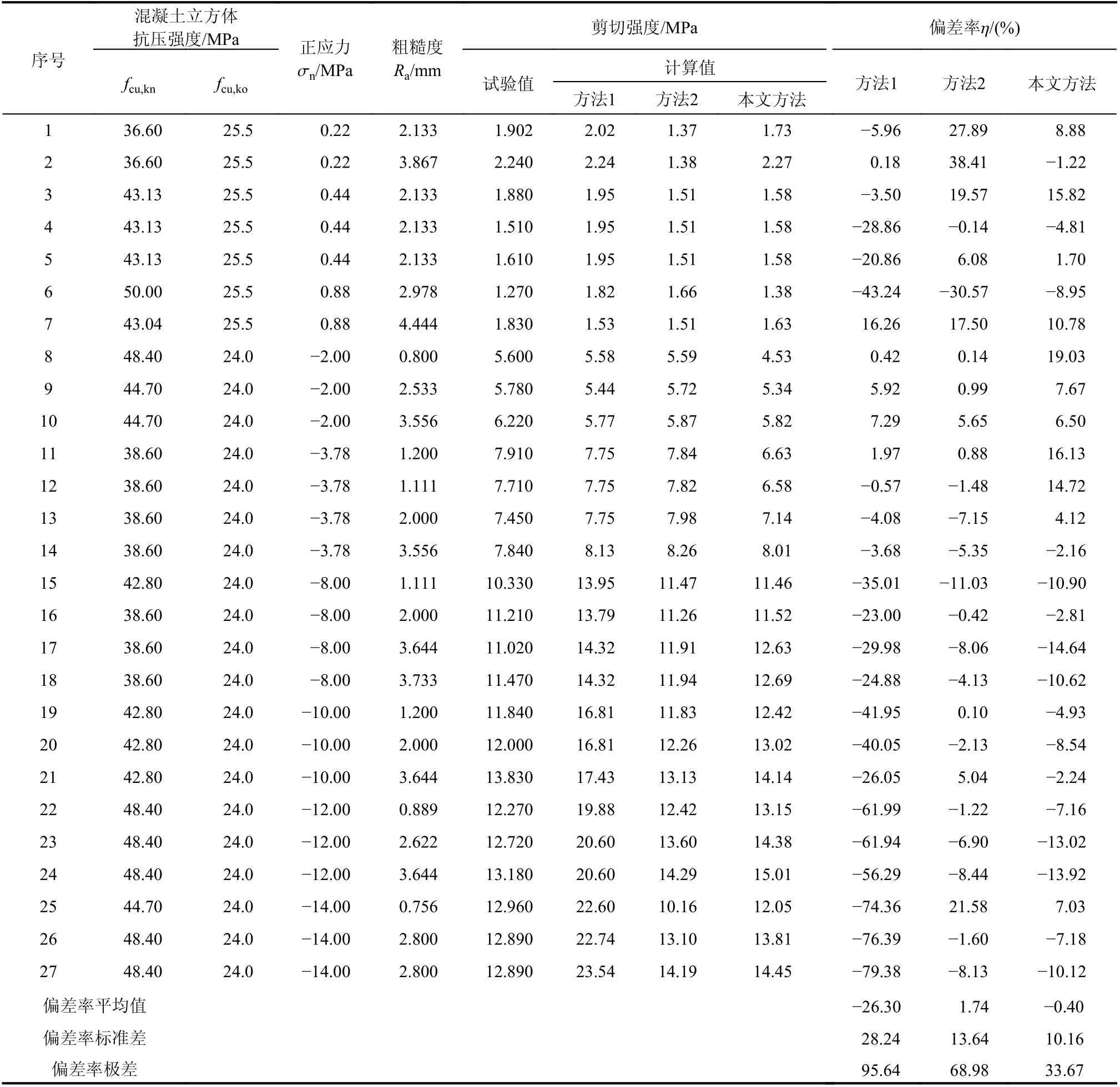
表3 新老混凝土压(拉)剪试件参数、不同方法计算值与偏差率Table 3 Parameter information of new-to-old concrete compression-shear (tension-shear) specimens and calculated values and deviation rates of calculation formulas

本文方法、已有方法计算值与试验值的比较如图2 所示，偏差率分布如图3 所示。从中可以看出：本文方法计算值与试验值的偏差率基本都在±15%以内，方法1 与方法2 的计算结果与试验值的偏差率均存在远大于±15%的情况。本文方法偏差率平均值为-0.40%，标准差为10.16%，最大正偏差率为19.03%，最大负偏差率为-14.64%，极差为33.67%；方法1 的偏差率平均值为-26.30%，标准差为28.24%，最大正偏差率为16.26%，最大负偏差率为-79.38%，极差为95.64%；方法2 偏差率平均值为1.74%，标准差为13.64%，最大正偏差率为38.41%，最大负偏差率为-30.57%，极差为68.98%。本文方法的平均值(绝对值)最低，为0.40%，以后按递增顺序依次为方法2(1.74%)、方法1(26.3%)；本文方法标准差最低，为10.16%，以后按递增顺序依次为方法2(13.64%)、方法1(28.24%)；本文方法极差最小，为33.67%，以后按递增顺序依次为方法2(68.98%)、方法1(95.64%)。

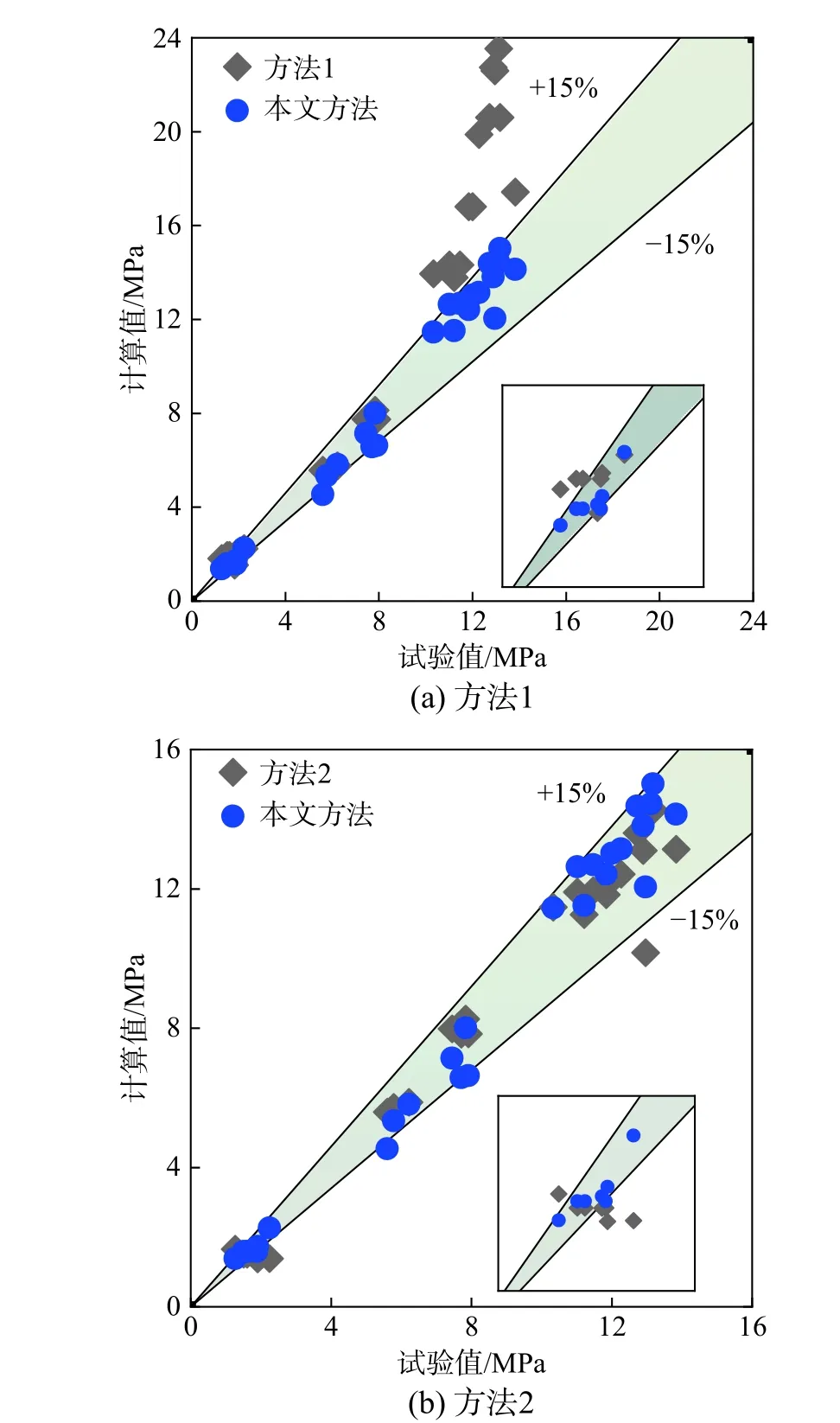
图2 本文方法、已有方法计算值与试验值的比较Fig. 2 Comparison of calculated values and experimental values of the methods in this paper and in existing papers

图3 本文方法、已有方法计算值的偏差率分布Fig. 3 The deviation rate distribution of the calculated values between the methods in this paper and in existing papers

不同方法偏差率随正应力变化如图4 所示，从图中可以看出，对于拉(剪)试件，方法1 和方法2 都存在偏差率远大于20%的情况。对于压(剪)试件，本文方法和方法2 的计算偏差受压应力影响不大，计算偏差都在20%以内；方法1 的计算偏差率随压应力的增大而增大，当压应力大于10 MPa 时，计算偏差为负偏差且大于40%，当压应力为14 MPa 时，偏差率最大达到了-79.38%，会过高估计试件的抗剪强度。

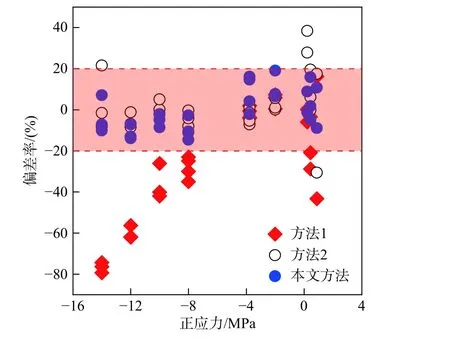
图4 不同方法偏差率随正应力变化Fig. 4 Different methods deviation rate changes with normal stress

3.2.2 纯剪试验试件

为了解本文方法对于新老混凝土结合面在纯剪受力情况下，计算新老混凝土无锚筋结合面抗剪强度的有效性，分别采用本文方法、不考虑正应力的方法3、方法4、方法5、方法6 和方法7分别对文献[2, 16 - 17, 19 - 20, 25]中的30 个新老混凝土结合面纯剪切受力试验试件的抗剪强度进行计算，并进行对比分析，纯剪切试验试件参数如表4 所示。新老混凝土纯剪试件试验结果与计算值见表5，计算值与试验结果的偏差率见表6。

表4 新老混凝土纯剪试件参数Table 4 Parameter of new-to-old concrete pure shear specimens

表5 新老混凝土纯剪试件试验结果与计算值Table 5 Experimental results and calculated values of new-toold concrete pure shear specimens

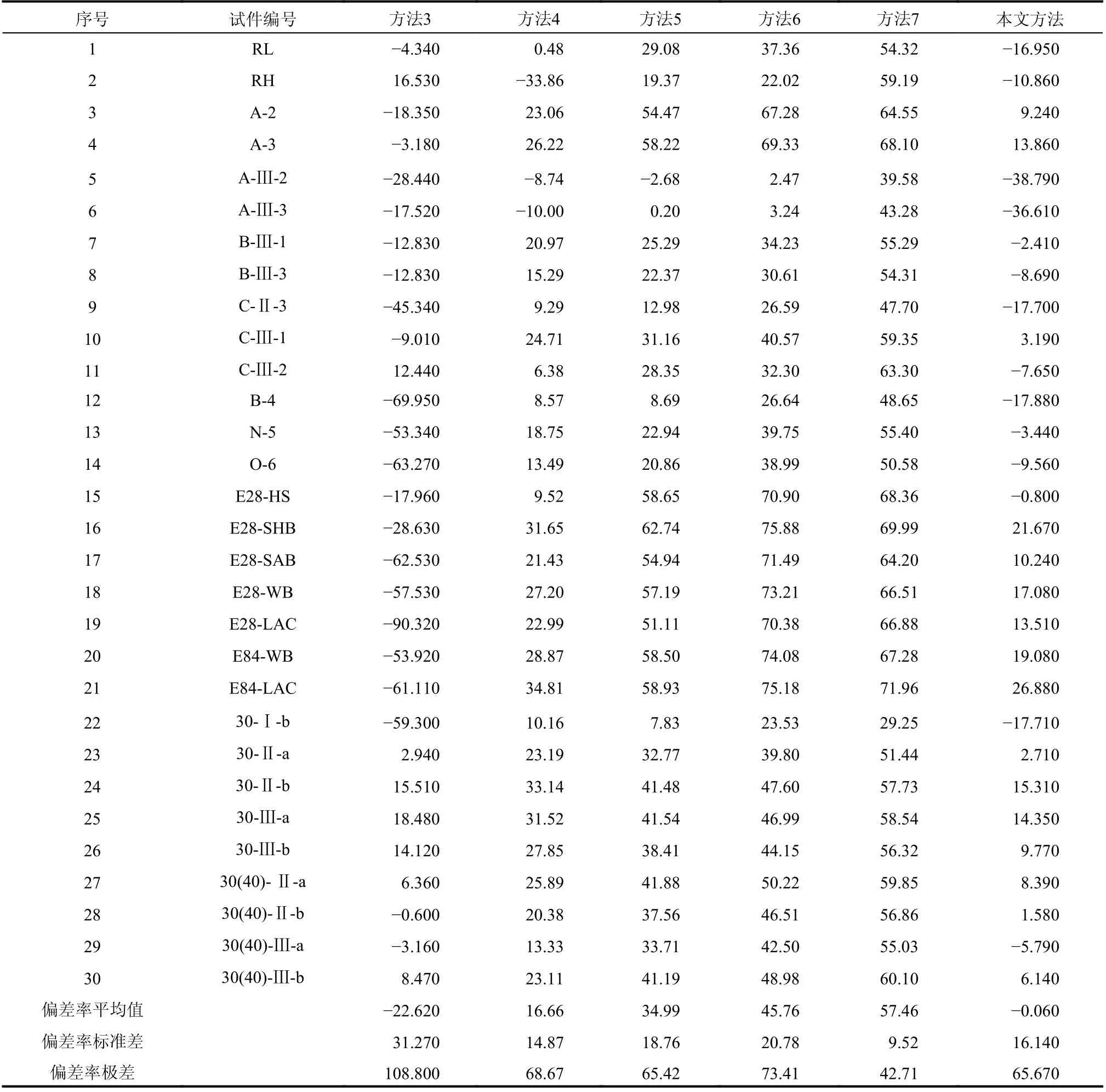
表6 新老混凝土纯剪试件抗剪强度计算值与试验结果的偏差率η/(%)Table 6 Deviation rate of shear strength calculated values and experimental values of new-to-old concrete pure shear specimens

文献[2]的试件形式为双面剪切试件，文献[19]的试验形式采用的是矩形短梁的推剪试验，文献 16 - 17, 25]采用的试件形式为Z 形剪切试件。30 组试验数据结果均用纯剪切强度表示。

本文方法、已有方法计算值与试验值对比如图5 所示，不同方法计算值偏差率分布如图6 所示。从中可以看出：本文方法除在计算低新老混凝土强度(25, 26.7)时，出现了-38.79%的较大偏差外，其余计算结果的偏差率大都在20%以内，而方法3、方法4、方法5、方法6 和方法7 都存在偏差率远高于20%的情况；方法3 根据试验数据(粗糙度范围为1.8 mm～3.0 mm)将粗糙度影响系数标定为常数0.06956，对于不在此粗糙度范围的情况可能存在较大的计算误差，如粗糙度为0.119 的试件编号为E28-LAC 的计算值与试验值偏差率高达-90.32%。方法4 的形式为相对抗剪强度与粗糙度呈线性相关，显然这也是要规定粗糙度范围的，当过高的追求粗糙度会对老混凝土表面造成较大的扰动，致使老混凝土受损反而降低了结合面的黏结性能，粗糙度为0.119 的试件编号为E84-LAC 的偏差率达34.81%。方法5 对低强度混凝土(25, 26.7)试件的计算结果最好，偏差率为-2.68%、0.20%，而对于高强度混凝土组(60.3,55.4)与(78.9, 68.3)均出现超过50%的偏差率，故对于高强度混凝土存在低估抗剪强度的情况。方法6对低强度混凝土(25, 26.7)试件的计算结果较好，其余试件计算值均小于试验值，最大偏差率达75.88%，原因在于是该方法仅考虑结合面粗糙度的影响，并未考虑新、老混凝土强度的影响。方法7 则是对所有试件的计算值均小于试验值，偏差率在29.25%～71.96%，说明考虑黏聚力安全系数的计算结果是偏保守的。

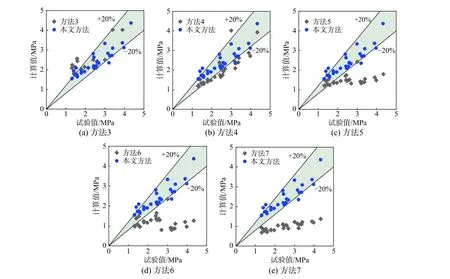
图5 本文方法、已有方法计算值与试验值对比Fig. 5 Comparison of calculated values and experimental values of the method in this paper and in existing papers

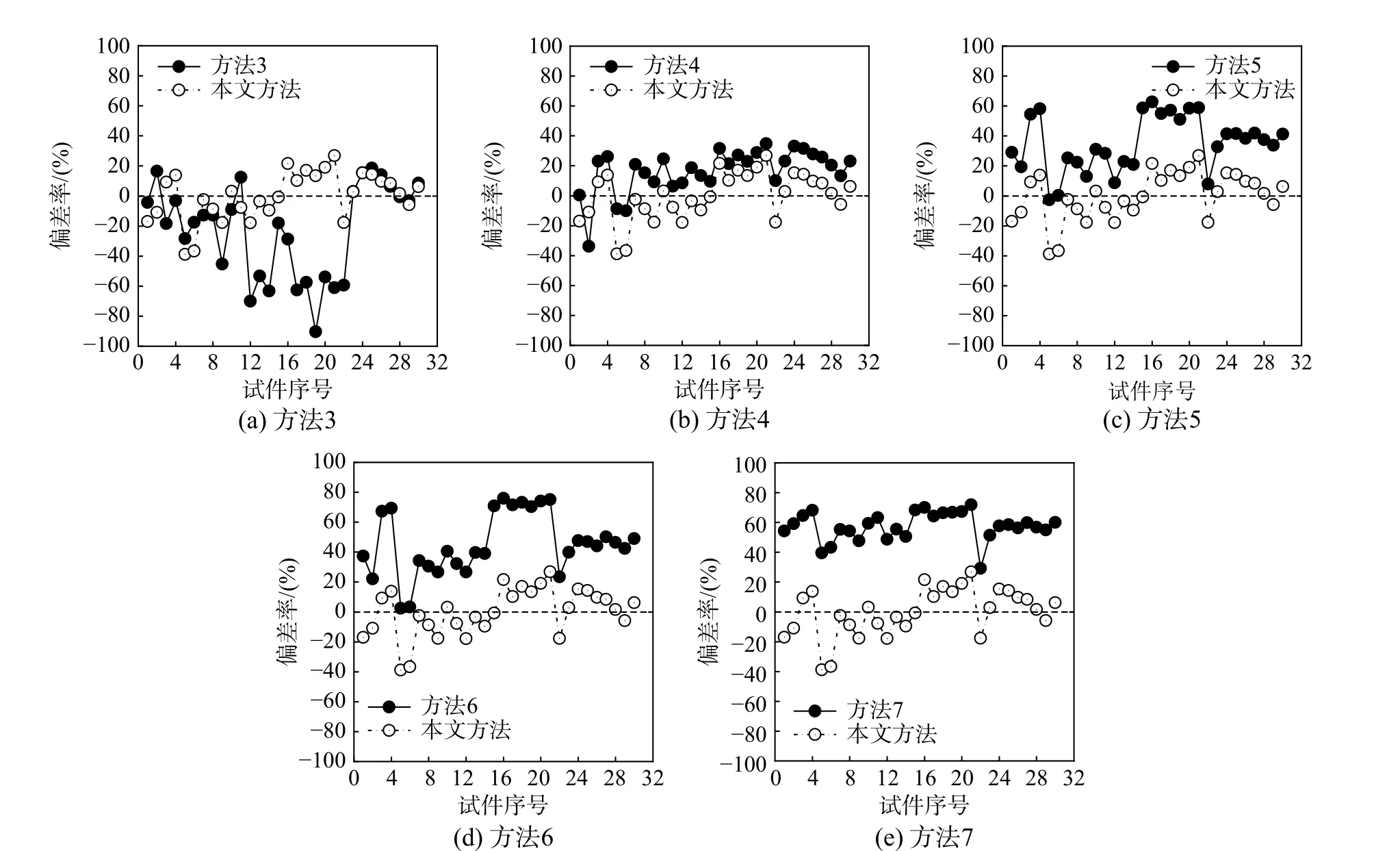
图6 本文方法、已有方法计算值的偏差率分布Fig. 6 The deviation rate distribution of the calculated values between the method in this paper and in existing papers

图7 为不同计算方法的偏差率平均值(绝对值)、标准差的比较情况。从图7(a)可以看出，本文方法的偏差率平均值(绝对值)最低为0.06%，以后按递增顺序依次为方法4(16.66%)、本文方法3(22.62%)、方法5(34.99%)、方法6(45.76%)和方法7(57.46%)。从图7(b)可以看出，方法7 的偏差率标准差最低，为9.52%，以后按递增顺序依次为方法4(14.87%)、本文方法(16.14%)、方法5(18.76%)、方法6(20.78%)和方法3(31.27%)。

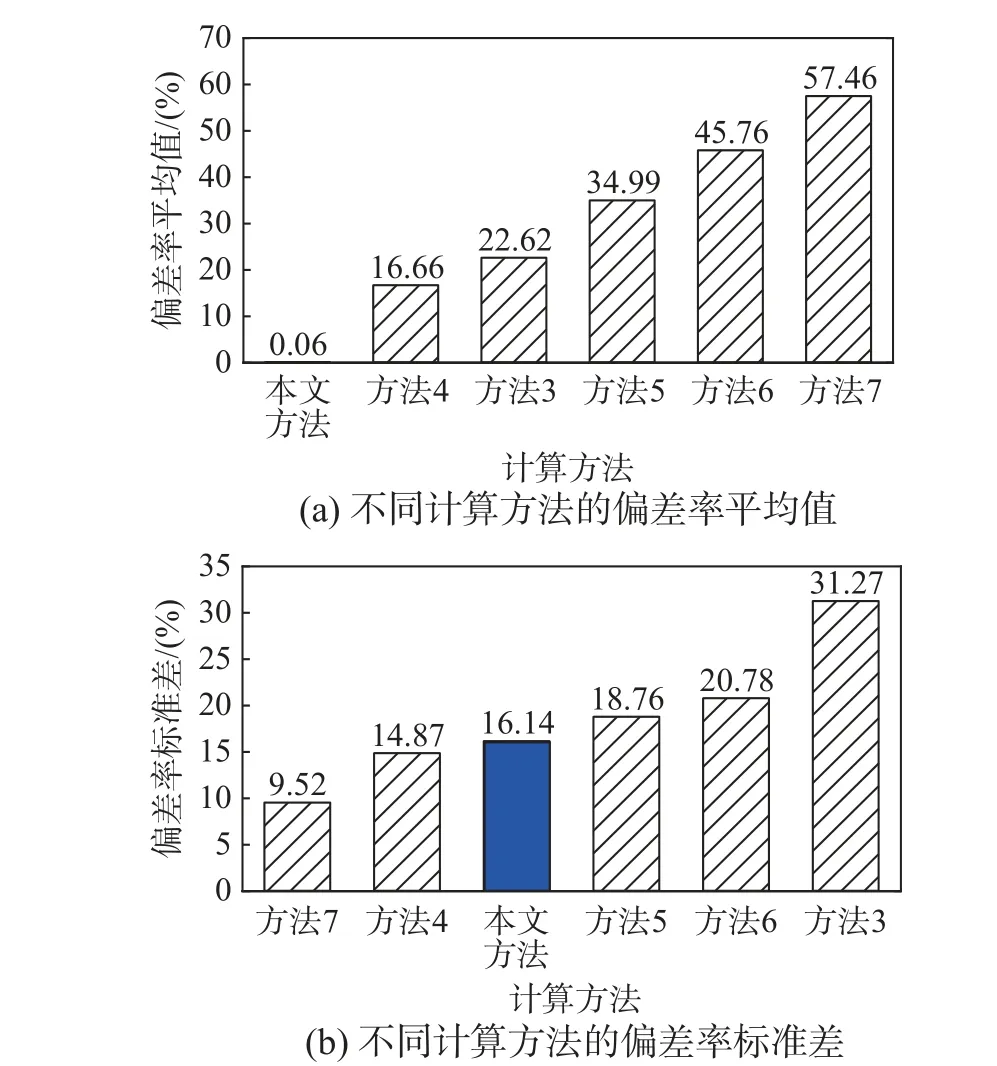
图7 不同方法的偏差率平均值(绝对值)、标准差比较Fig. 7 Comparison of average (absolute value) and standard deviation of the deviation rate of different calculation methods

图8 为不同计算方法的最大正负偏差率及极差比较情况。从图中可以看出，极差最小的为方法7(42.71%)，本文方法和方法5 的极差基本接近，分别为65.67%和65.42%，以后按递增顺序依次为方法4(68.67%)、方法6(73.41%)和方法3(108.8%)。

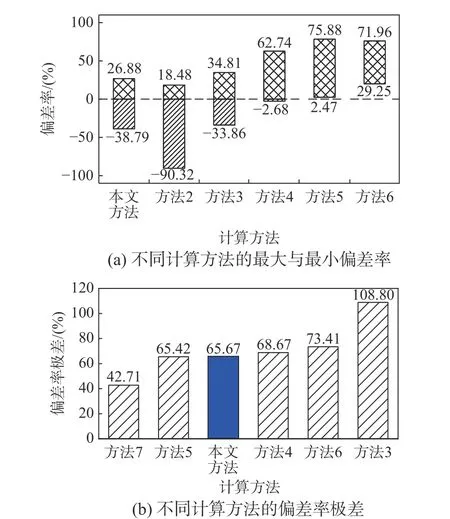
图8 不同计算方法的最大偏差率及极差比较Fig. 8 Comparison of maximum deviation rate and range of different calculation methods

不同计算方法计算纯剪试验试件偏差率平均值(绝对值)、极差和标准差排序如表7 所示。不同计算方法相对于试验值的计算精度由好到差分别为：从平均值方面考虑依次为本文方法、方法4、方法3、方法5、方法6 和方法7；从极差方面考虑依次为方法7、方法5、本文方法、方法4、方法6 和方法3；从标准差方面考虑依次为方法7、方法4、本文方法、方法5、方法6 和方法3。

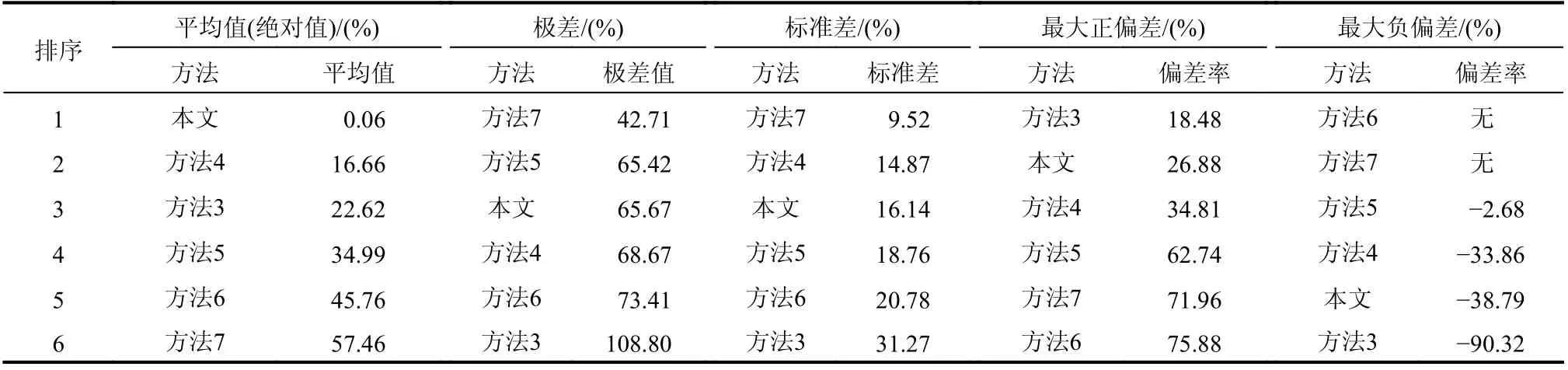
表7 不同计算方法计算纯剪试验试件偏差率平均值(绝对值)、极差和标准差排序Table 7 The average (absolute value), different calculation methods calculate range and standard deviation of the deviation rate of pure shear test specimens

对于新老混凝土无锚筋结合面纯剪试件抗剪强度计算，本文方法计算值与试验值的偏差率平均值(绝对值)最低，为0.06%，偏差率极差为65.67%、标准差为16.14%，最大正偏差率为26.88%，最大负偏差率为-38.79%；方法3 的最大正偏率为18.48%，偏差率平均值(绝对值)为22.62%，而偏差率极差、标准差、最大负偏差率分别为108.8%、31.27%和-90.32%；方法4 的偏差率为16.66%，偏差率极差和标准差分别为68.67%和14.87%，最大正偏差率为34.81%，最大负偏差率为-33.86%；方法5 的偏差率平均值为34.99%，偏差率极差和标准差分别为65.42%和18.76%，最大正偏差率为62.74%，最大负偏差率为-2.68%；方法6 的偏差率平均值为45.76%，偏差率极差、标准差分别为73.41%和20.78%，最大正偏差率为75.88%，无负偏差；方法7 的极差、标准差分别为42.71%和9.52%，偏差率平均值、最大正偏差率分别为57.46%和71.96%，无负偏差。总体而言，本文方法计算值与试验值的偏差率平均值(绝对值)最低，其他方法的偏差率平均值(绝对值)均远大于本文方法；本文方法计算结果的偏差率大都在±20%以内，除计算低强度混凝土试件偏差率为-38.79%，较大之外；方法3 最大负偏差太大，且离散度较大；方法4 最大正偏差率也远大于本文方法；方法5、方法6、方法7 的计算值大于试验值较多，太过于保守，且离散度较大。

综上所述，本文所提出的新老混凝土无锚筋结合面抗剪强度统一计算方法，既可用于压(拉)剪复合受力构件，也可应用于纯剪受力构件，理论依据充分、计算简便，计算精度优于已有计算方法。

4 结论

基于三维能量屈服准则、虚功原理和塑性极限分析理论，详细推导新老混凝土无锚筋结合面抗剪强度理论计算公式，引入考虑正应力和粗糙度的综合影响系数进行修正，构建新老混凝土无锚筋结合面抗剪强度统一计算公式，并采用试验数据进行验证，采用不同方法对27 个新老混凝土无锚筋结合面压(拉)剪复合受力试验试件以及30 个新老混凝土无锚筋结合面纯剪试验试件进行抗剪强度计算，并进行对比分析，主要结论如下：

(1) 本文所提出的无锚筋结合面抗剪强度统一计算公式既可用于压(拉)剪复合受力构件，也可应用于纯剪受力构件结合面抗剪强度计算。

(2) 对于新老混凝土无锚筋结合面压(拉)剪复合受力试验试件，本文方法计算值与试验值的偏差基本都在±15%以内，统一计算公式的计算精度高于现有考虑正应力的计算方法；对于新老混凝土无锚筋结合面纯剪试验试件，本文方法除计算低强混凝土试件偏差率较大之外，其余计算结果的偏差率大都在20%以内，本文所提出的统一计算公式的计算精度远高于已有不考虑正应力的计算方法。

(3) 所提出的新老混凝土无锚筋结合面抗剪强度统一计算方法，理论依据充分、计算简便，计算精度优于已有计算方法。