高速铁路沿线轻钢类建筑物失效运动路径数值仿真研究
2022-05-05张丽君孙新宇
张丽君 赵 雷 孙新宇
(1. 西南交通大学, 成都 610031;2.中国国家铁路集团有限公司, 北京 100844)
结构风效应的数值模拟是利用计算流体动力学方法通过计算机模拟建筑结构周围风场,确定作用在建筑结构上的风效应,称为数值风洞[1-6]。与一般流体动力学问题不同的是,风绕建筑物流动主要涉及高雷诺数湍流、分离流和强三维流动,其核心是湍流问题[7-9]。国内外专家对大风作用下房屋结构的安全性开展了大量的研究[10-13],但是,难以满足高速铁路沿线轻钢类建筑物安全评估的需求,尤其是未能确定其运动轨迹,以指导高速铁路路外环境整治。基于此,本文利用数值仿真分析,模拟高速铁路沿线轻钢类建筑物-门式刚架轻钢建筑的4个风向角流场及4个风速流场,并结合N-S方程采用稳态方法进行求解,分析不同风速、风向下建筑表面风荷载的变化规律,采用ICFD计算模块进行流固耦合分析,揭示不同风速、风向下与连接失效屋面板的风致漂移规律。
1 数值模拟方法验证
TTU模型(Texas Tech University Building Model)试验是风工程学界的标尺模型之一,对风工程研究产生了广泛影响。TTU模型与本次试验模型均为典型的低矮双坡建筑,通过对比计算TTU模型,可验证本文数值模拟方法的准确性。
1.1 模型概述
模型几何尺寸为9.1 m×13.7 m×3.93 m,坡度约为1/60,如图1所示。建立CFD数值模型,选用RANS Spalart-Allmaras模型为湍流模型。
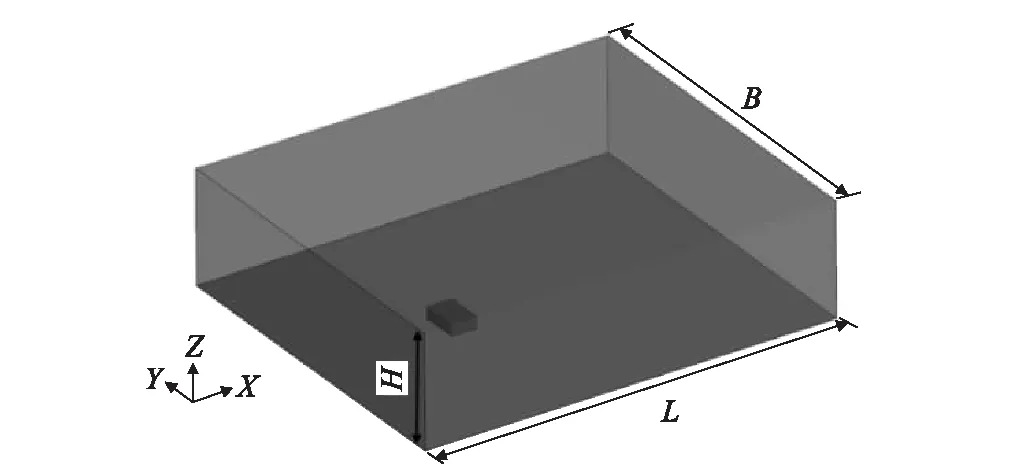
图1 计算域图
(1)计算域尺度
B×H×L=124.128 m×39.88 m×147.52 m,阻塞比为1%<5%。
(2)边界条件
速度剖面如式(1)所示。
(1)
式中:v10——10 m高度的风速;
Α——粗糙度指数;
Z——实际流场相对大气边界层底部的高度;z10取10 m。
(3)网格划分
采用四面体网格,流场核心区网格加密,最小网格尺度0.15 m,计算流域最大网格尺度约2.27 m,位于流场出口位置附近。
1.2 计算结果
TTU模型数值模拟风压系数如图2所示。模型的迎风面主要以正压为主,风压系数在0.51以上;背风面主要以负压为主,风压系数在 -0.33~-0.53之间;屋盖为负压,屋盖的风压系数普遍在 -0.12~-0.53范围内;建筑物侧面为负压,风压系数普遍在-0.12~-0.53范围内。屋盖和建筑物侧面存在很强的来流分离现象,形成分离区,分离区受负压,风压系数超过-1。

图2 TTU模型风压系数图
将数值模拟结果与TTU实测中轴位置的风压系数对比,结果吻合较好,表明本文的数值风洞计算方法可靠,对比结果如1所示。

表1 风压系数对比表
2 建筑表面风荷载数值模拟
2.1 模型概述
分析模型为门式刚架轻型房屋钢结构,模型尺寸为6 m×3 m×4.5 m(长×高×宽),模型墙面与屋面均采用YX35-125-750(V-125)型单层压型钢板,屋面板与檩条采用自攻螺钉波峰连接。经计算分析发现风荷载作用时计算域36 m×25 m×45 m范围外的风场稳定,不影响建筑物的表面风荷载,为提高模型的计算效率,故取模型的计算域为36 m×25 m×45 m(B×H×L),如图3所示。
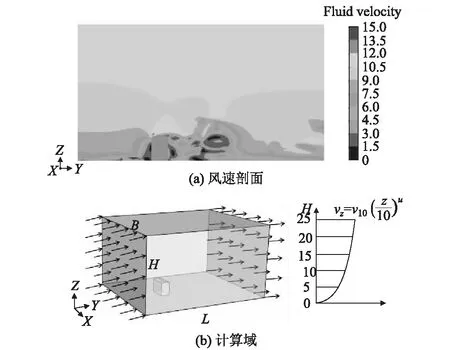
图3 计算域示意图
2.2 计算结果与分析
2.2.1 A区风荷载
4个风向角下计算建筑A区表面风荷载曲线如图4所示。风荷载普遍小于0,为风吸力。当风向角一定时,随着速度的增加,风荷载增加。当风向角为0°时,A区表面风载曲线呈抛物线型,其中A-4区和A-5区的荷载较大,风荷载在 -40~-620 N范围内;当风向角为30°时,A区表面风荷载曲线呈抛物线型,在A-5区位置风荷载最大;当风向角为60°时,A区表面风荷载曲线在A-2区和A-3区位置发生突变;当风向角为90°时,A区表面风荷载在A-1区位置风荷载最大,在A-4区~A-6区位置风荷载较小接近0。4个风速下计算建筑A区表面风荷载曲线如图5所示,相同风速下,随着风向角的增加,风荷载普遍减小,风向角为0°时风荷载最大,但是在A-1区是90°风向角时风荷载最大。

图4 4个风向角下A区表面风荷载曲线图

图5 4个风速下A区表面风荷载曲线图
2.2.2 B区风荷载
4个风向角下计算建筑B区表面风荷载曲线如图6所示,风荷载普遍小于0,为风吸力。当风向角一定时,随着速度的增加,风荷载增加。当风向角为0°时,A区表面风载曲线呈抛物线型,其中B-4区和B-5区的荷载较大,风荷载在 -10~-350 N范围内;当风向角为30°时,在B-1区位置风荷载最大,B-8区位置风荷载最小;当风向角为60°时,B区表面风荷载曲线在先增加再趋于平稳,在B-1区位置风荷载最大,B-3区以后风荷载变化不明显;当风向角为90°时,B区表面风荷载在B-1区位置风荷载最大,在B-4区~B-6区位置风荷载较小且接近0。4个风速下计算建筑B区表面风荷载曲线如图7所示,相同风速下,随着风向角的增加,风荷载普遍先增加后减小,风向角为30°时风荷载最大,但是在B-1区是90°风向角时风荷载最大。
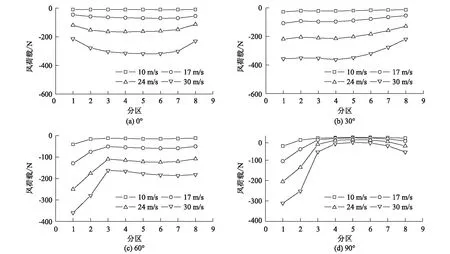
图6 4个风向角下B区表面风荷载曲线图

图7 4个风速下B区表面风荷载曲线图
3 试验模型流固耦合模拟
3.1 模型概述
根据稳态计算结果可知屋盖风压系数较侧壁风压系数较高,屋盖受风吸作用较大。为提升计算效率,选取受风载作用最大区块进行屋面板风致飘逸轨迹模拟分析,采用LS-Dyna的ICFD计算模块进行流固耦合分析。根据建筑表面风荷载分析,筛选试验模型表明受风吸作用最大的板块进行流固耦合模拟,即:0°风向角下选择A-4区板块;45°风向角下选择A-5区板块;90°风向角下选择A-1区板块。计算时,0~2 s约束板块,2 s后释放板块的约束,使其在风力作用下运动,并提取屋面板运动轨迹。为提高计算效率,将YX35-125-750(V-125)型单层压型钢板简化为截面惯性矩等效的矩形钢板。
3.2 计算结果及分析
3.2.1 风场变化分析
经模拟分析,不同风速作用下,风场变化相似,因此,风速为30 m/s,风向为0°的风场进行说明,屋面板运动过程中的风场变化如图8所示。结果表明:t=0 s时,屋面板未发生运动,此时建筑物内部风速为0 m/s;t=2 s时,屋面板被掀起,并发生运动,此时来流风涌入建筑物内部,带动建筑物内部流场,导致建筑物内部风场发生变化,此时内部风速可达约16 m/s,此时建筑物内部风场逐渐趋于稳定;t=4 s时,屋面板距建筑物约14 m,建筑物内部风场稳定,风速最高可达约18 m/s,建筑物附近风场稳定,在屋面板附近局部风场发生变化。

图8 风场变化图
3.2.2 屋面板运动轨迹分析
(1)工况1(风向角:0°;风速:30 m/s)
工况1屋面板位移时程曲线如图9所示,屋面板整体运动时间约43 s。t=0 s时,屋面板受风吸力作用,此时屋面板受力大小约613.18 N,导致屋面板整体斜向脱开建筑物;受到风力作用下,屋面板在y轴正方向运动,由于风场变化,屋面板在运动过程中伴随旋转等运动姿态,加之受重力作用,屋面板在约43 s时刻触地,此后不再移动。在此期间,屋面板的运动距离约569.65 m,其中x轴方向运动距离约59.9 m,y轴方向运动距离约566.5 m。屋面板整体运动轨迹线如图10所示。

图9 工况1屋面板位移时程曲线图

图10 工况1屋面板运动轨迹图
(2)工况2(风向角:45°;风速:30 m/s)
工况2屋面板位移时程曲线如图11所示,屋面板整体运动时间约21.8 s。t=0 s时,屋面板受风吸力作用,此时屋面板受力大小约281.30 N,导致屋面板整体斜向脱开建筑物;受到风力作用下,屋面板在y轴正方向运动,由于风场变化,屋面板在运动过程中伴随旋转等运动姿态,加之受重力作用,屋面板在约21.8 s时刻触地,此后不再移动。在此期间,屋面板的运动距离约283.8 m,其中x轴方向运动距离约4.36 m,y轴方向运动距离约283.77 m。屋面板整体运动轨迹线如图12所示。
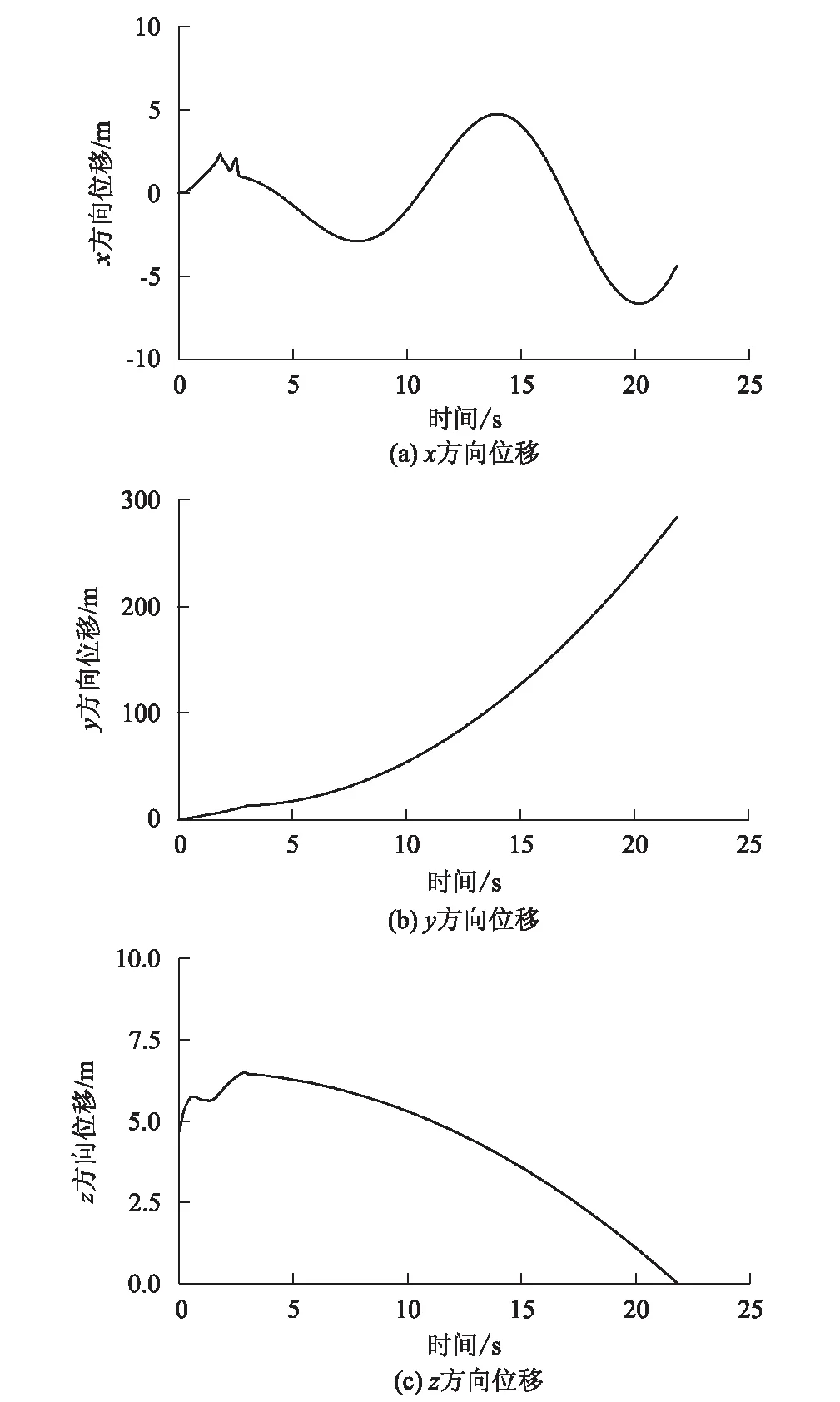
图11 工况2屋面板位移时程曲线图
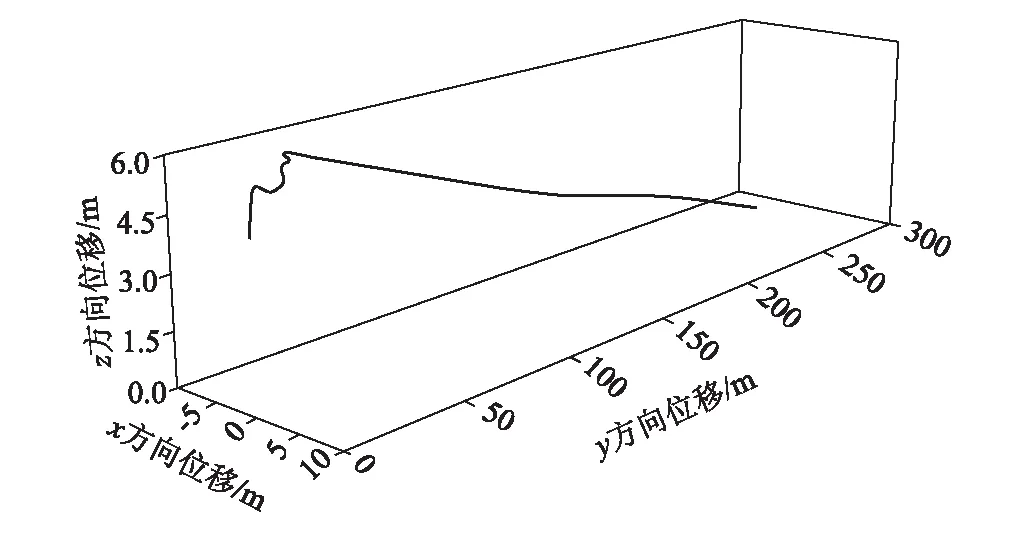
图12 工况2屋面板运动轨迹图
(3)工况3(风向角:90°;风速:30 m/s)
工况3屋面板位移时程曲线如图13所示,屋面板整体运动时间约34.6 s。t=0 s时,屋面板受风吸力作用,此时屋面板受力大小约317.06 N,导致屋面板整体斜向脱开建筑物;受到风力作用下,屋面板在y轴正方向运动,由于风场变化,屋面板在运动过程中伴随旋转等运动姿态,加之受重力作用,屋面板在约34.6 s时刻触地,此后不再移动。在此期间,屋面板的运动距离约277.28 m,其中x轴方向运动距离约16.81 m,y轴方向运动距离约276.77 m。屋面板整体运动轨迹线如图14所示。

图13 工况3屋面板位移时程曲线图
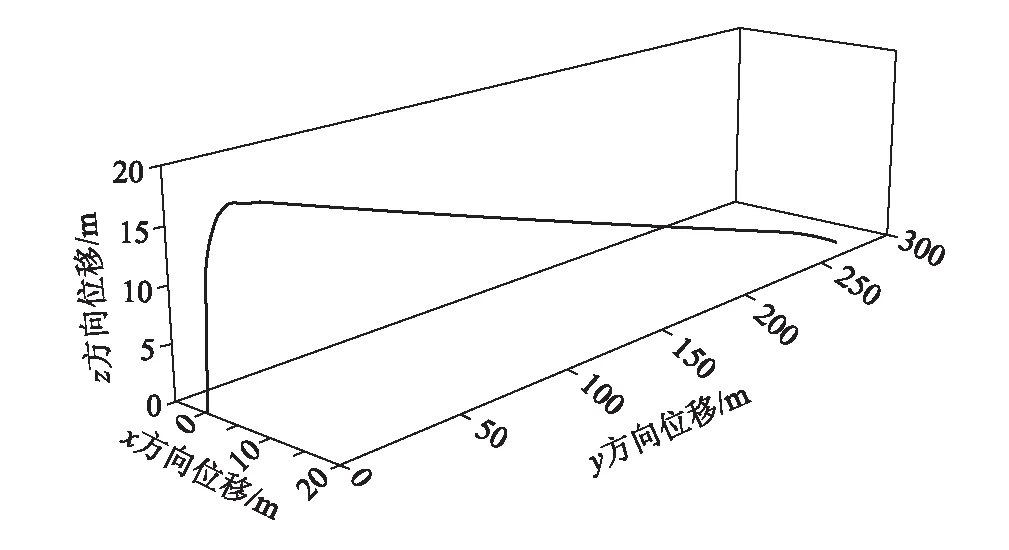
图14 工况3屋面板运动轨迹图
(4)工况4(风向角:0°;风速:24 m/s)
工况4屋面板位移时程曲线图15所示,屋面板整体运动时间约27.4 s。t=0 s时,屋面板受风吸力作用,此时屋面板受力大小约382.38 N,导致屋面板整体斜向脱开建筑物;在风力作用下,屋面板在y轴正方向运动,由于风场变化,屋面板在运动过程中伴随旋转等运动姿态,加之受重力作用,屋面板在约27.4 s时刻触地,此后不再移动。在此期间,屋面板的运动距离约69.1 m,其中x轴方向运动距离约-2.13 m,y轴方向运动距离约69.07 m。屋面板整体运动轨迹线如图16所示。

图15 工况4屋面板位移时程曲线图

图16 工况4屋面板运动轨迹图
(5)工况5(风向角:0°;风速:17 m/s)
工况5屋面板位移时程曲线如图17所示,屋面板整体运动时间约5.6 s。t=0 s时,屋面板受风吸力作用,此时屋面板受力大小约179.40 N,导致屋面板整体斜向脱开建筑物;在风力作用下,屋面板在y轴正方向运动,由于风场变化,屋面板在运动过程中伴随旋转等运动姿态,加之受重力作用,屋面板在约5.6 s时刻触地,此后不再移动。在此期间,屋面板的运动距离约17.38 m,其中x轴方向运动距离约-1.23 m,y轴方向运动距离约17.34 m。屋面板整体运动轨迹线如图18所示。
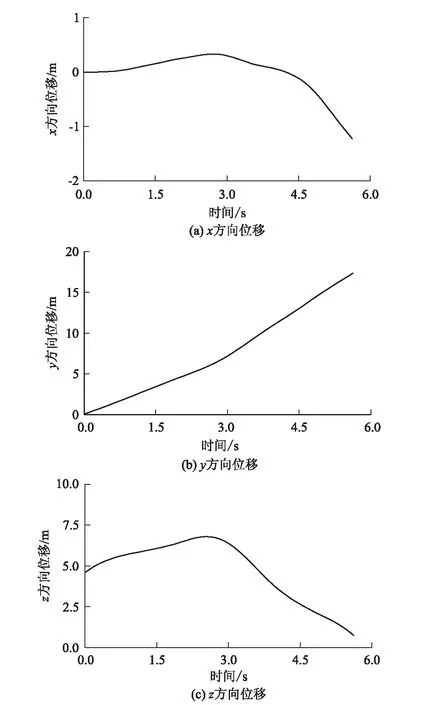
图17 工况5屋面板位移时程曲线图

图18 工况5屋面板运动轨迹图
根据上述结果可知,在相同风速下,不同风向角作用下,屋面板受风吸力作用不同,在风向角为0°时,屋面板受风吸力作用最大,屋面板运动距离最远;不同风速工况下,随着风速的增加,屋面板运动距离增加。屋面板位移对比如图19所示。
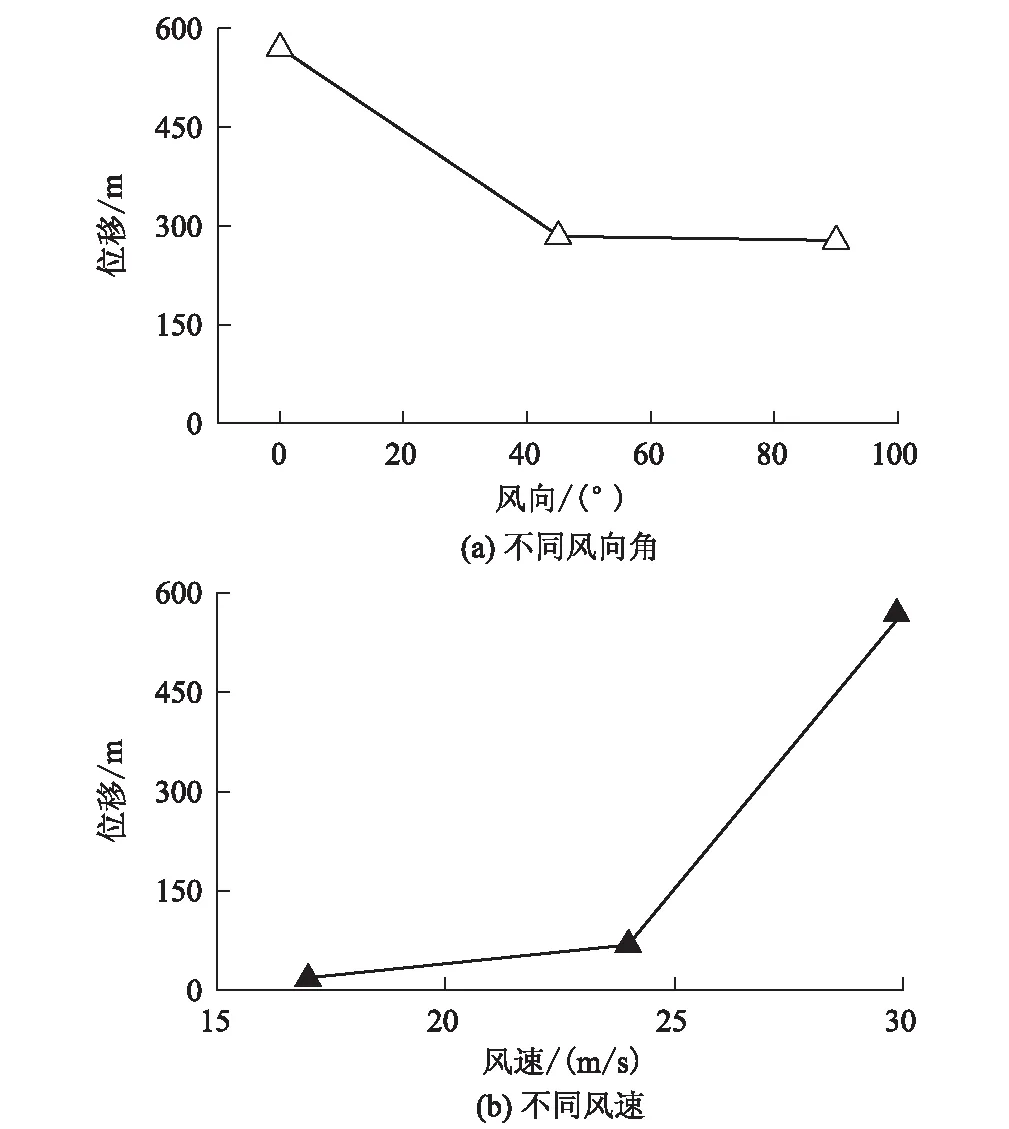
图19 屋面板位移对比图
4 结论
根据上述分析,可得如下结论:
(1)基于TTU场地模型实测数据,采用本文数值模拟方法准确反演了其建筑表面风压系数分布,验证了该数值模拟方法的有效性。
(2) 不同风载工况下,屋盖受风吸作用最明显,屋盖风载系数最大可达-2,但随着风向角的变化,受风吸作用最明显的板块也在变化,其中0°风向角下A-4板块风载最大,90°风向角下A-1板块风载最大,且随着风速的增加,屋盖受到的荷载增加,当风速达到30 m/s时,屋盖风荷载可达最大值约616.63 N。建议采用该风吸荷载值为计算依据,反算不同规格自攻螺钉的合理布置间距,形成螺钉规格与间距查询对照表,据此快速排查防护范围内轻钢建筑的安全性。
(3)试验模型在风载作用下,屋盖受风力作用最明显,可能引起屋盖脱开建筑物,导致建筑物内部风场变化,使建筑物内部受较大风力作用;屋盖飞行过程中也会引起整体流域风场变化。计算结果表明:在相同风速下,不同风向角作用下,屋盖受风吸力作用不同,在30 m/s风速作用下,在风向角为0°时,屋盖受风载作用最大,屋盖运动距离最远约569.65 m;在不同风速工况下,随着风速的增加,屋盖运动距离增加。偏安全考虑,建议高铁沿线两侧600 m作为外部环境安全防护距离。
