基于LSTM-ResNet模型的定点有效波高预测

李自立，蒙素素

（广西师范大学电子工程学院，广西 桂林 541004）

1 引言

海洋波浪高度的短期预测对人类海洋活动的开展有着极为重要的意义[1-2]，例如，对于海上航行、海上施工、渔业捕捞和海上军事等活动，波高短期预测精度越高，海上活动相关状况的应对就会越充分。在海洋数值预测研究中，有效波高的短期预测一直都是热点和难点问题[3]。海浪有效波高预测方法主要分为经验预测法和数值模型预测法[4]。经验预测法是通过对历史观测得到的海浪数据按照时间先后进行外推，进而得到相关海浪状态的预期数值[5]，这种预测方法主要依靠历史数据和传统分析相结合，在实用性和准确度方面都存在较大局限性。随着数学科学的发展，海浪波高相关研究在数值建模新领域获得了一些具有较高研究价值的数值模型，如SWAN（Simulating WAve Nearshore）、WAVEWATCH-Ⅲ以及WAM（Wave Model）等。数值模型的结果是基于大量数据计算得到的，对计算量和计算速度有着较高的要求，在数据不是很充分的情况下，其计算精度存在较大的局限。随着近几年神经网络和深度学习技术的兴起，人们尝试搭建各种神经网络或混合模型来预测海浪高度。比如Makarynskyy 等[6-7]以波高数据为输入搭建了神经网络；Tsai等[8]将反向传播（Back Propagation，BP）神经网络技术应用于短期海浪预测和数据补充，取得了较好的效果；Fan 等[9]将长短期记忆网络（Long Short-Term Memory，LSTM）应用于波高预测，提高了有效波高的预报精度；Mandal 等[10]利用时域单变量建模和递归神经网络预测波高；Zhang 等[11]构造了受限波尔兹曼机-深度置信网络模型，具有较好的波高短期预测能力。本文在前人研究的基础上，把深度残差网络（Residual Network，ResNet）理论引入到长短期记忆网络技术中，对北部湾特定海域的波浪数据进行建模研究，尝试获得一个置信度较高的波高数值模型，并依据此网络对有效波高进行短期预测分析，通过多网络算法对比验证模型的有效性与预测的准确度。

2 数据准备

本实验研究数据由国家海洋局南海信息中心提供，为2016—2018年北部湾海域定点浮标实测数据，有效波高的最小采样间隔为1 h，数据的样本点总数为26 277 个。为了能够准确地分析波高的数学特征和分布状况，我们对实测有效波高进行了特征分析，结果见表1。

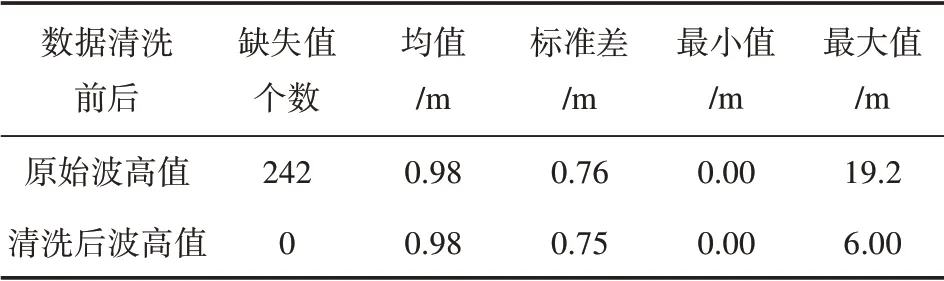
表1 定点浮标有效波高数据值分析结果Tab.1 The analysis results of the effective wave height data of the fixed-point buoy

表1中原始数据的缺失值为242个，缺失数据只占总值的9.21%，对整体数据分析的误差影响极小。为了批量数据分析的便捷，将缺失值用前向填充法对其进行插值处理。经过数据清洗后有效波高的数值统计特征如下：均值为0.98 m，标准差为0.75 m，最小值为0 m。当有效波高数值达到6 m及以上时，可定义为灾难性海浪[12-13]，此海况出现的几率小，有很强的偶然性，对长时的模型预测研究意义不大。为了方便研究有效波高的长时规律，本文将超过6 m的数值全部限幅为6 m。本文设定模型输入为当前时刻6 h前的波高数据，网络标签数据设置为预测当前时刻未来6 h 的波高数据。实验时，选取总数据的80%为训练集，用于模型建模训练；剩余的20%为模型的测试集，用于模型预测效果测试分析。

3 基于LSTM-ResNet的模型原理

随着层数的增加，单一堆叠的LSTM 网络模型会发生梯度消失和网络性能的退化问题，因此，本文引入ResNet 模块接入LSTM 层生成LSTMResNet 模型。该模型由ResNet 模块和LSTM 模块组成。模型总体构图如图1所示。

图1 中上方LSTM 层中32 表示隐藏层数量，整流线性单元（Rectified Linear Unit，ReLU）为激活函数，第一个箭头左边的数字代表当前输入6 个时间刻度和1个变量，这里省略了Batch_Size维度。

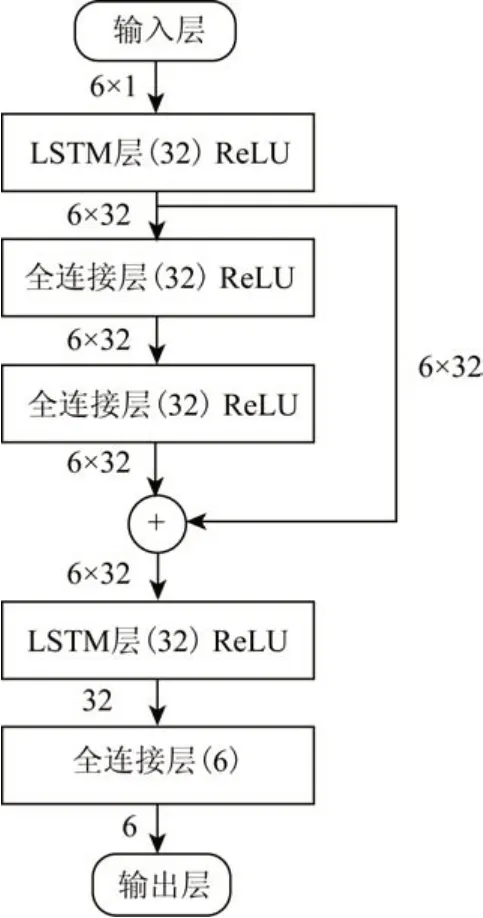
图1 LSTM-ResNet模型总体结构图Fig.1 Overall structure of the LSTM-ResNet model

3.1 长短期记忆网络

循环神经网络（Recurrent Neural Network，RNN）是一种节点定向连接成环的人工神经网络。与前馈神经网络（Feedfoward Neural Network，FNN）不同的是，RNN 可以利用它内部的记忆来处理任意时序的输入序列，这让其可以更容易处理如不分段的手写识别或语音识别等。然而，当连续时间数据的输入序列加长时，就会造成网络训练时梯度爆炸和梯度消失的问题，从而使RNN网络丧失长期记忆的功能。Hochreiter 等[14]在1997 年提出LSTM 模型，通过设计门结构来避免梯度消失等问题，门结构使得LSTM单元可以保存和获取长时间周期的上下文信息。LSTM单元结构图如图2所示[9]。

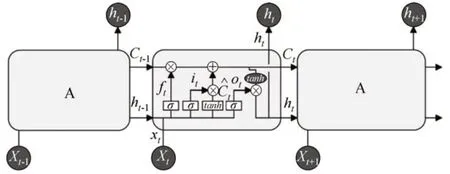
图2 LSTM单元的原理图Fig.2 Schematic diagram of the LSTM unit

图2中各参数的计算公式如下：

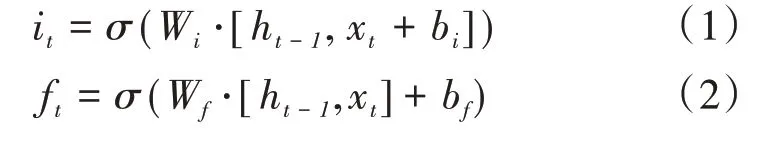
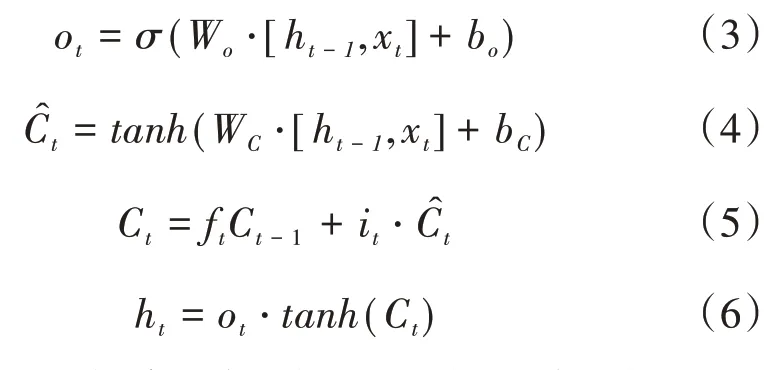
式中，it、ft和ot分别为输入门、遗忘门和输出门；xt为当前时刻的输入特征；Wi、Wf、Wo和Wc为待训练参数矩阵；bi、bf、bo和bc为训练偏置项；σ表示激活函数；ht-1为隐藏层前一时刻的输出。

式（1）—（3）经过Sigmoid 激活函数使得3 个门的大小在0～1 之间；式（4）是当前信息和前一步信息归纳形成的新记忆C^t，从而实现信息的更新；式（5）通过遗忘门去忘记一些旧信息再同时加入一些新信息；式（6）主要是把过滤好的信息输出，当有多层循环网络时，当前层网络的输入xt是前一层网络提取出来的有用信息ht。

3.2 残差网络

残差网络作为2015 年ImageNet 竞赛（Image Net Large-Scale Visual Recognition Challenge）的冠军，其top5错误率（预测的前5个类别中不包含正确类别的比例）为3.57%。VGGNet（Visual Geometry Group Net）和GoogLeNet（Google Inception Net）的成功，说明网络越深，模型表现越良好。然而，单纯堆叠神经网络层数会使网络模型退化，导致后面的特征丢失了前边特征的原本模样，产生梯度消失或者梯度爆炸等问题，造成训练和测试效果变差。为了解决模型“退化”的问题，崔文植[15]提出了残差结构（见图3）。

图3 残差网络的核心结构Fig.3 The core structure of the residual network

图3 是ResNet 的核心结构图。如图所示，ResNet 加入了一根跳连线后，其输入可以直接短连接到非线性层的输出上，输出结果为直接连接过来的恒等映射x和非线性输出F（x）两路值元素的对应相加。这个步骤能有效缓解神经网络模型堆叠导致的梯度消失问题。

4 仿真和讨论

4.1 评估指标

为了评价不同神经网络的预测效果，本文采用均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）、均方误差（Mean Squared Error，MSE）和相关系数R2来反映预测效果。公式如下:

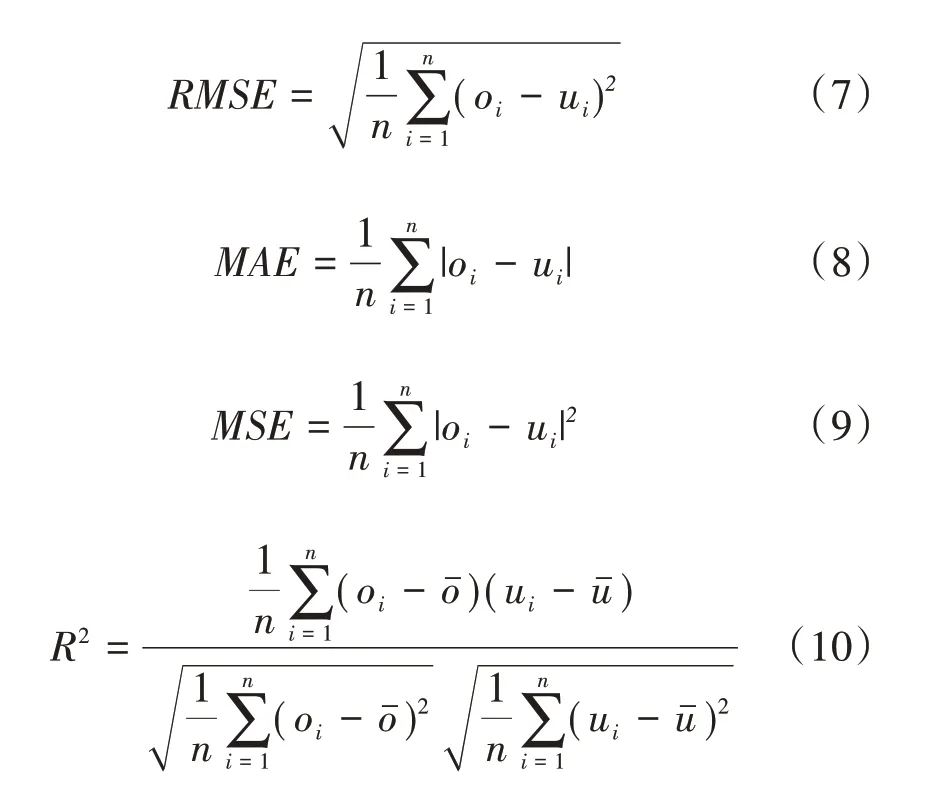
式中，oi为预测值；ui为观测值；为预测值的平均值；为观测值的平均值；n为样本数量。

根据MAE、MSE、RMSE 和R2的结果来判断模型的好坏，结果的取值范围均为[0，1]。前3 个评价指标的值越接近0，说明模型拟合效果越好；R2越接近1，表示模型拟合效果越好。

4.2 有效波高的短期时刻预测结果

为了验证模型的预测性能，采用表1 清洗过的有效波高序列为研究对象，将其输入LSTM-ResNet模型、LSTM 模型和ResNet 模型以及目前应用最广泛的BP 模型进行对比试验。4 种模型的隐藏层数量均设置为32个，且都采用ReLU激活函数。

4.3 结果分析

表2 列出了4 种算法的有效波高短期预测结果，最优结果以粗体显示。数值结果表明LSTMResNet 网络的短期预测效果最优，在1 h 的预测中MAE 低 至0.08 m，R2高 至0.96。 ResNet 网 络、LSTM 网络和BP 网络的总体预测效果与实测数据基本一致，但是预测精度没有LSTM-ResNet 网络高。随着预测时间的逐渐加长，数据的有效性不断降低，4 种算法的MAE 数值逐渐增大，R2数值不断减小，LSTM-ResNet 网络的性能衰减程度相对较慢，尽管MAE 最高达到了0.23 m，R2最多下降至0.70，但是预测结果还是处于可以接受的精度范围内。

表2 短期预测的性能结果比较Tab.2 Comparison of performance results for short-term forecasting

图4 为浮标实测值和4 种算法的有效波高1 h预测数值对比图，图中的曲线变化对比表明LSTMResNet 网络在预测波高的变化趋势和数值稳定性方面都表现出优于其他算法的效果。基于LSTM网络的周期性结构和门机制，本文设计的网络在信息选取上具有优势，相较于其他算法能够获得最优信息；在加入ResNet网络并对网络进行层数加深设置后，网络计算的数值精度得到较大的提高，综合以上算法优点取得了波高预测与浮标数据拟合度较好的结果。与之对比的LSTM 网络、BP 网络和ResNet 网络，预测结果与浮标数值虽然也具有一定的一致性，但是在某些时刻或者时间段上出现了预测值相对滞后的情况。

图4 1 h时间范围内观测结果与算法结果的比较图Fig.4 Comparison of observation results and algorithm results in the time range of 1 hour

图5 为2018 年5 月6 日3：00—9 月8 日9：00 基于LSTM-ResNet 网络的有效波高间隔1 h 和6 h 的数值预测对比图。相对于6 h 的预测结果，1 h 的预测结果在数值上与浮标测量值更贴近。虽然6 h 的预测结果偏差略大，但总体预测的曲线变化趋势与浮标测量值基本一致，进一步验证了LSTM-ResNet网络在短时间隔的有效波高预测方面的有效性。

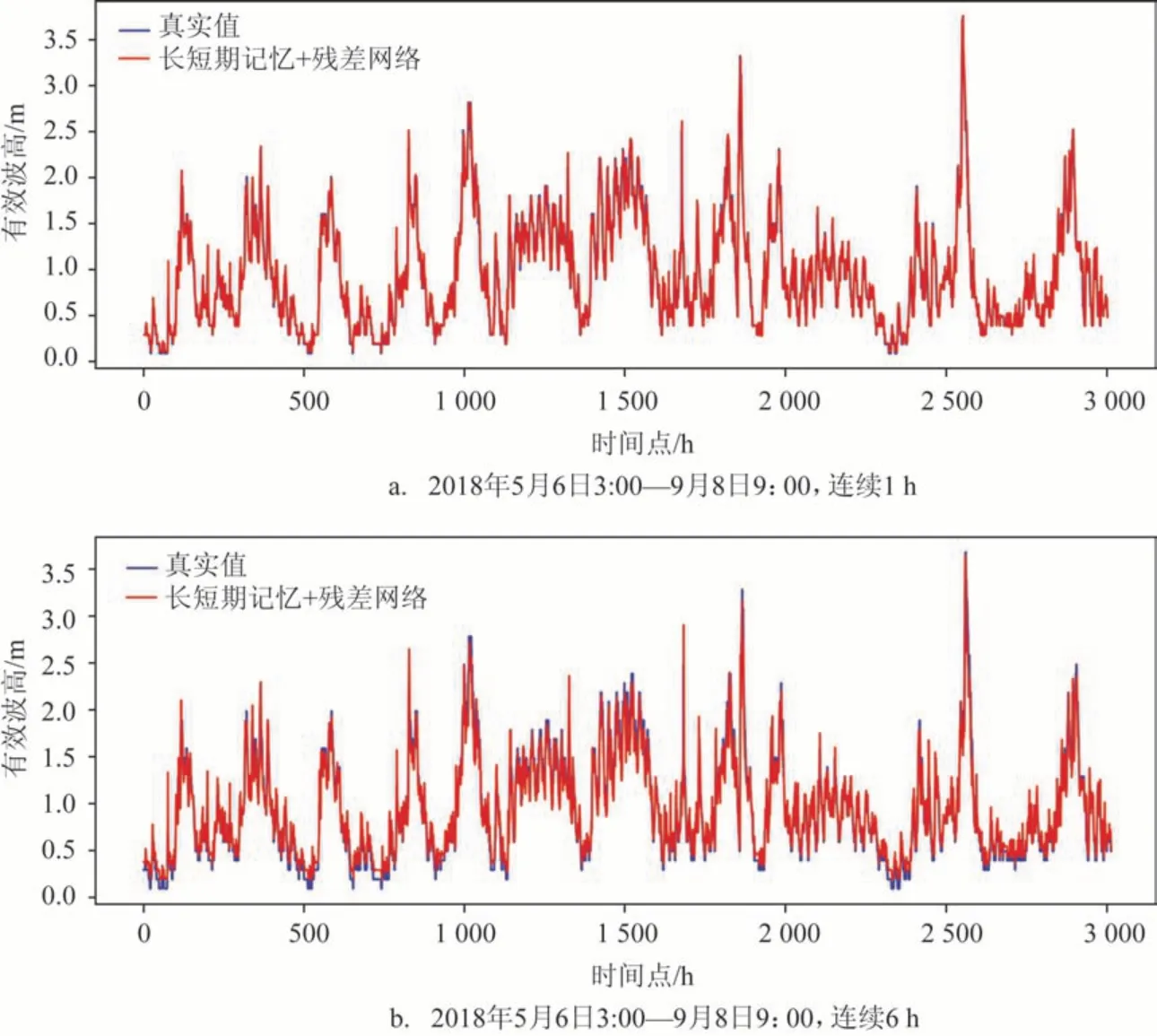
图5 预测值与观测值对比图Fig.5 Comparison of predicted and observed values

5 结论

本文运用神经网络的相关模型方法，对北部湾海洋有效波高的变化规律进行了数值建模，并进行了数值预测研究与结果对比分析。将4种网络模型方法的波高数据建模预测数值结果进行对比，结果表明本文采用的LSTM-ResNet 网络模型在短时有效波高预测中能够取得比较好的结果。在浮标实测数值的结果对比分析中，采用4 个统计指标对预测结果进行综合评价，本文采用的LSTM-ResNet网络预测结果与实测数值的一致性最好，预测的时间容许范围最大，相较于其余对比方法，在短时有效波高预测上具有一定的实用性，因此在海洋数值预测中具有一定的应用潜力。