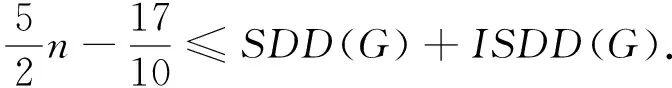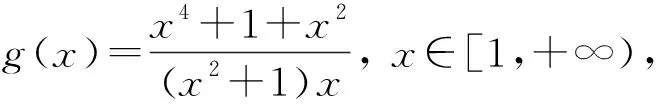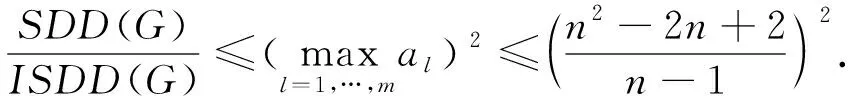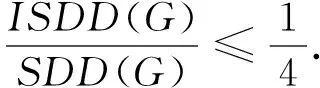图的对称分割指数的界
2022-05-05李小丽邵燕灵
李小丽,邵燕灵
(中北大学 理学院,山西 太原 030051)
0 引 言
本文讨论的图G均为简单连通无向图.设图G=(V(G),E(G))为n阶无向图,其顶点集V(G)={v1,v2,…,vn},边集E(G),|E(G)|=m,di为顶点vi的度,i=1,2,…,n; 用e=vivj表示其端点为vi,vj的边,若其中di=1,则称vi为悬挂点.
图G的最小度记为δ,最大度记为Δ,用p表示图G中悬挂点的个数.

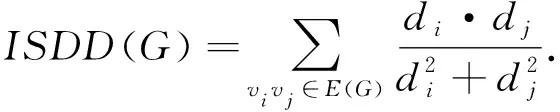
本文主要通过对图G最大度Δ、最小度δ的奇偶性分类讨论得到了图的对称分割指数SDD(G)的下界,然后,利用一些熟知的不等式给出了SDD(G)+ISDD(G),SDD(G)-ISDD(G),SDD(G)/ISDD(G)的关系.
1 对称分割指数的下界


引理2[15]设图G有m条边,最小度为δ,最大度为δ+1,β表示图G中满足du+dv=2δ+1的边uv∈E(G)的个数,则β是偶数.
定理1设图G有m条边,最小度为δ,最大度为δ+1,β表示图G中满足du+dv=2δ+1的边uv∈E(G)的个数,则
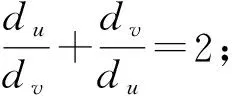
定理2设图G有m条边,最小度为δ,最大度为δ+1,则

证毕.
定理3设图G有m条边,最小度为δ,最大度为Δ>δ+1,记β0,β1,β2分别为G中的边集A0={uv∈E(G):du=δ,dv=Δ},A1={uv∈E(G):du=δ,δ 证毕. 定理4设图G是n阶连通图,有m条边,最小度为δ,最大度为Δ>δ+1,则 证明设A0,A1,A2,β0,β1,β2如定理3中所定义,由于G是连通图,故A0非空,或A1与A2均非空. 若A1与A2均非空,则β1≥1,β2≥1,故由定理3得 证毕. 定理5设图G是n阶连通图,有m条边,最小度为δ,最大度为Δ>δ+1. 1) 若δ是偶数,则 SDD(G)≥2m+ 2) 若Δ是偶数,则 SDD(G)≥2m+ 证明设A0,A1,A2,β0,β1,β2如定理3中所定义.令m1为图G中满足du+dv=2δ的边uv∈E(G)的边数,n1为图G中du=δ的顶点的个数,m2为图G中满足du+dv=2Δ的边uv∈E(G) 的边数,n2为图G中du=Δ的顶点的个数.因图G是连通图,故有n1δ-β0-β1=2m1,n2Δ-β0-β2=2m2. 若β0=1,则β1≥1,由定理3得 若β0=0,则β1≥2,β2≥1,由定理3得 SDD(G)≥2m+ 若β0=1,则β2≥1,由定理3得 若β0=0,则β2≥2,β1≥1,由定理3得 SDD(G)≥2m+ 证毕. 定理6设图G是n阶连通图,有m条边,最小度为δ,最大度为Δ>δ+1. 1) 若δ是偶数,则 2) 若Δ是偶数,则 因此, 定理7设图G为n阶树,n≥3,则 当且仅当图G为Pn时左边等号成立,图G为Sn时右边等号成立. du≥dv. 若图G同构Pn,则 SDD(Pn)+ISDD(Pn)=2g(2)+ 若图G不同构Pn,此时图G中的悬挂点P≥3,则 SDD(G)+ISDD(G)≥3g(2)+(n-4)g(1)= SDD(G)+ISDD(G)-(SDD(Pn)+ISDD(Pn))≥ 可得 (1) 当且仅当图G同构Pn时式(1)等号成立. SDD(G)+ISDD(G)≤(n-1)g(n-1)= (2) 当且仅当图G同构Sn时式(2)等号成立.证毕. 定理8设图G为n阶树,n≥3,则 当且仅当G为Pn时左边等号成立,图G为Sn时右边等号成立. 若图G同构Pn,则 SDD(Pn)-ISDD(Pn)=2g(2)+ 若图G不同构Pn,此时图G中的悬挂点P≥3,则 SDD(G)-ISDD(G)≥3g(2)+ SDD(G)-ISDD(G)-(SDD(Pn)-ISDD(Pn))≥ 故 (3) 当且仅当图G同构Pn时式(3)等号成立. SDD(G)-ISDD(G)≤(n-1)g(n-1)= (4) 当且仅当图G同构Sn时式(4)等号成立.证毕. 定理9设图G为n阶连通图,n≥3,则 当且仅当G为Sn时左边等号成立,图G为Kn时右边等号成立. (5) 当且仅当a1=a2=…=am时等式(5)成立. 因为 故 (6) 当且仅当图G同构Sn时式(6)等号成立. (7) 只有式(5),式(6)等号同时成立时,式(7)等号才成立,因此,当且仅当图G同构Sn时式(7)等号成立. 又因为 所以 (8) 当且仅当图G同构kn时式(8)等号成立. 证毕.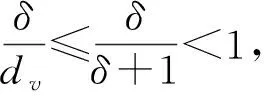
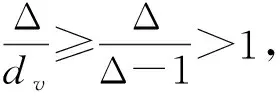
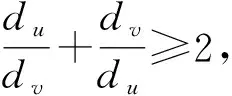
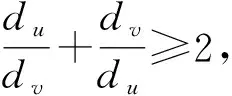

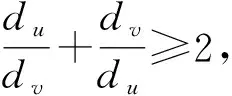

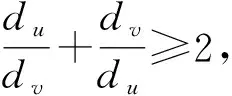
2 对称分割指数与反对称分割指数的一些关系