耐热垫块与步进炉水梁的焊接工艺优化

汪建新，邵和平，吴启明

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

现如今，国内各大钢铁热轧厂所使用的加热炉大部分都是步进式。步进式加热炉的整体结构具有复杂性，炉底机械是步进式加热炉的重要组成部分，其中水梁是炉底机械的主要承重构件，它是步进式加热炉设计的关键[1]。水梁结构由固定梁和步进梁两部分组成，是支撑和移动钢坯的部件。由于加热钢种的不同，炉内温度变化较大，水梁热胀冷缩现象严重。同时焊接处的产生的膨胀无法消除全部作用与水梁上，易产生焊接应力，如果不进行及时地消除将会产生焊接裂纹，最终造成水梁漏水[2]。

焊接结构在建筑、工业、化工、航空航天等领域得到广泛应用。在焊接过程中，焊接工艺起至关重要的作用，决定产品的焊接质量[3-4]。水梁的制造过程中，构件与构件之间的连接方式往往是通过焊接完成的。针对水梁漏水问题，改进耐热垫块与水梁之间的焊接工艺，采用垫块两端不进行焊接、小电流、多道焊缝，有效降低了水梁在制造过程中出现的人为因素。

本文主要以水梁上管道和隔热垫块为研究对象，运用焊接仿真软件SYSWELD做两者的焊接模拟，对比几种方案焊接过程中焊接残余应力的分布及变形，得到最佳的焊接工艺，对垫块焊接在水梁上结构优化具有重要意义。

1 有限元模型的建立

1.1 模型尺寸

如图1所示，为水梁和隔热垫块两者的剖面图，水梁上管道外径114 mm，内径为78 mm；垫块尺寸为150 mm×40 mm×80 mm，两端面与管道中心呈30°；焊接方式为四道焊，焊缝方向为纵向焊接。

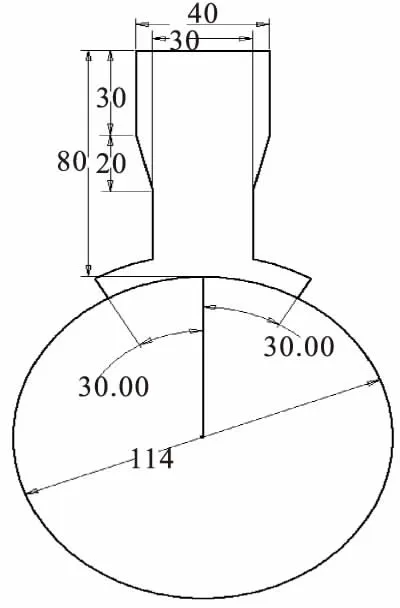
图1 耐热垫块与水梁的二维结构图

1.2 有限元模型的建立及网格划分

采用Visual-Mesh软件进行网格划分，过程中网格多采用六面体单元，尽量少采取四面体或者其他单元，避免出现函数不收敛或计算不准确的情况。对焊缝和热影响区近端划分较为细密的网格，在远端部分划分较为粗大的网格，如图2所示。

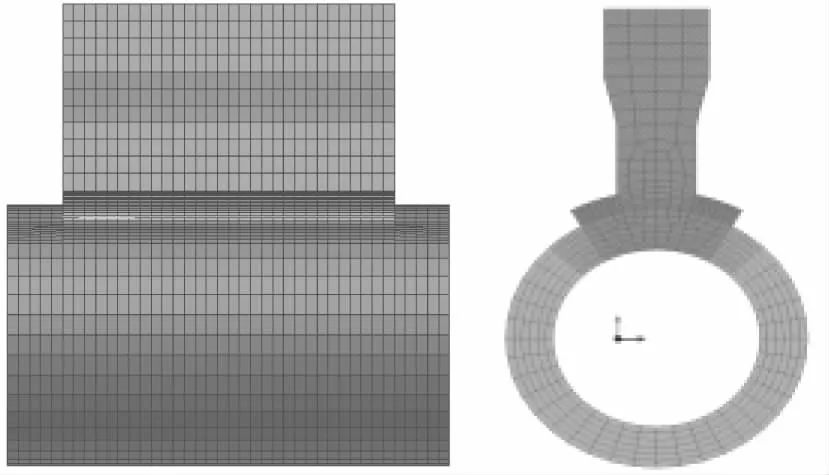
图2 有限元模型

1.3 材料性能参数

水梁采用的是20号钢，具有和很强的抗冲击能力，通常可进行弯折，并具有良好的热加工性能。不同温度下的材料属性[5]见表1。

表1 20 号钢材料属性

2 焊接参数

2.1 焊接方式

采用焊接方式为TIG焊，对称交替焊接的残余拉应力峰值是最低的[6]，焊接焊缝及顺序如图3所示。第1、2焊缝采用的电压为25～28 V，焊接电流为90～110 A，焊接速度为6～7 mm/s，第3、4焊缝采用的电压为27～30 V，焊接电流为110～140 A，焊接速度为3～4 mm/s。

图3 焊接焊缝示意图

在实际焊接过程中，因电弧的运动使熔化熔池前面与熔池后面的能量分布不一样的，电弧后面的加热区域大于电弧前面的加热区域。双椭球热源模型通过分析焊接过程中的上述特点，并充分考虑了焊接电弧在厚度方向的挖掘和搅拌作用。采用双椭球热源模型[7]如图4所示。

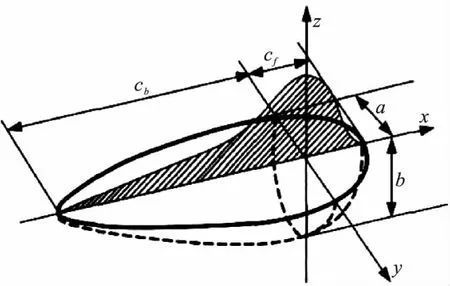
图4 双椭球热源模型

2.2 边界条件

焊接模拟的边界条件分为温度场和结构边界条件。温度场边界条件包括环境温度、热对流、热辐射；取环境温度为20 ℃，施加对热流和热辐射边界条件[8]。

结构边界条件采用两边管全约束，防止模型在仿真分析过程中发生刚性位移，如图5所示。

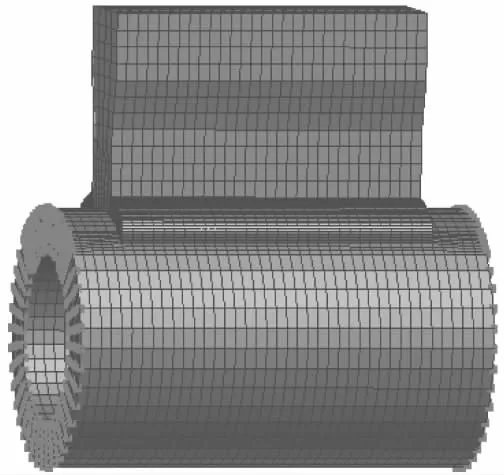
图5 约束条件施加图

焊接模拟采用间接耦合的方式，灵活性好，计算效率高。

3 焊接工艺优化

焊接工艺质量好与坏会影响水梁管道上的应力分布、变形等，因此对传统的焊接工艺进行改进，设置了六组方案进行对比：

方案一：两端进行满焊，采用的焊接顺序为1→2→3→4；

方案二：两端进行满焊，采用的焊接顺序为1→2→4→3；

方案三：两端进行满焊，采用的焊接顺序为1→3→2→4；

方案四：两端各留25 mm不焊接，采用的焊接顺序为1→2→3→4；

方案五：两端各留25 mm不焊接，采用的焊接顺序为1→2→4→3；

方案六：两端各留25 mm不焊接，采用的焊接顺序为1→3→2→4。

采用间接耦合方式[9]计算。

3.1 应力场分析

3.1.1 等效应力场分析

进行等效应力分析，给出两种不同方案的等效应力所在区域分布云图，列出了六种不同方案的等效应力最大值和最小值。如图6和表2所示。

图6 等效应力分布图

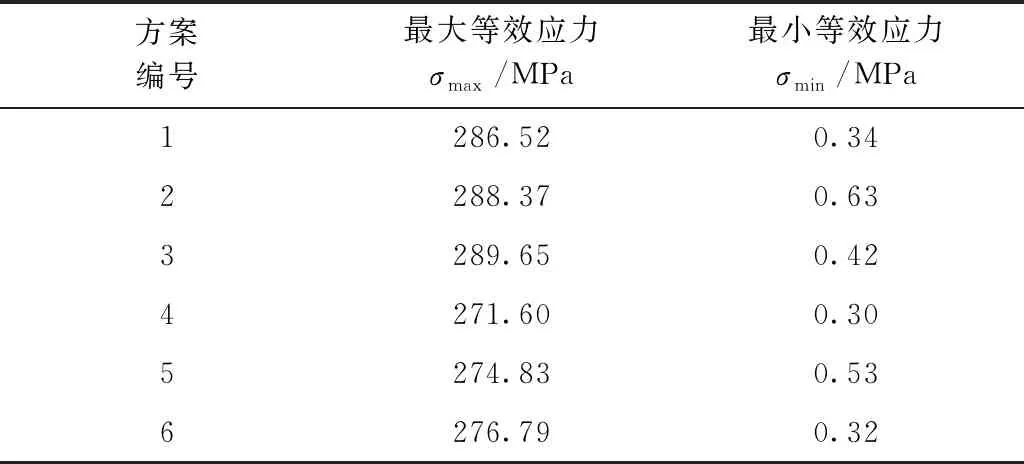
表2 六种方案的等效应力最值

由表2可知，方案一到方案六的等效应力最大值分别为286.52 、288.37、289.65、271.60、274.83、276.79 MPa。其中，方案四的等效应力值最低，方案三的等效应力值最高。

3.1.2 横向残余应力场分析

进行横向残余应力分析，给出两种不同方案的横向残余应力所在区域分布云图，列出了六种不同方案的横向残余应力最大值和最小值。如图7和表3所示。

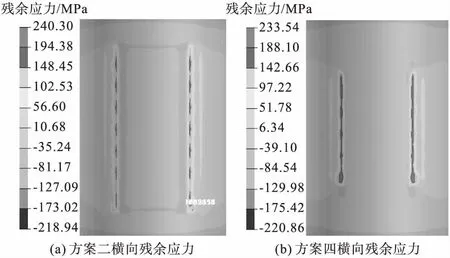
图7 横向残余应力分布图

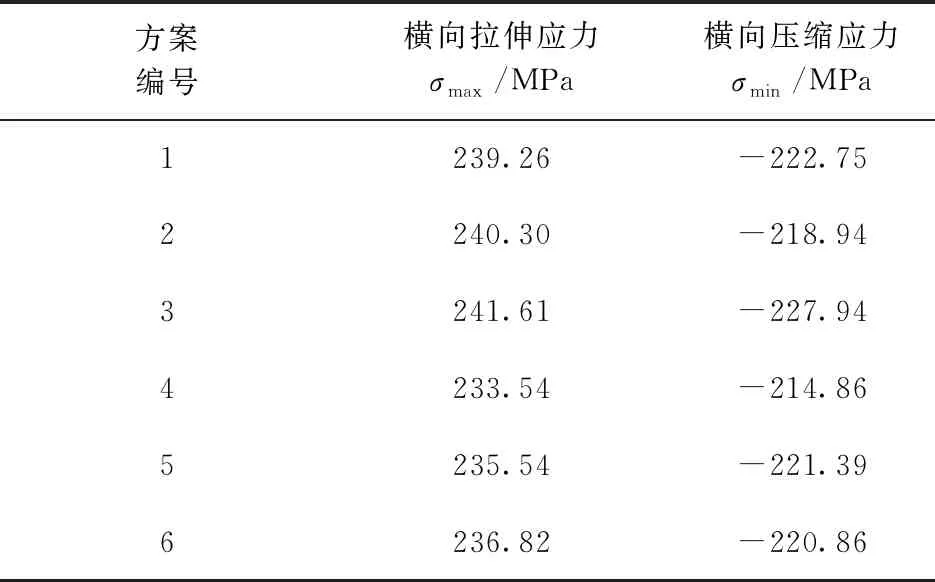
表3 六种方案的横向残余应力最值

由表3可知，方案一到方案六的横向拉伸应力最大值分别为239.26、240.30、241.61、233.54、235.54、236.82 MPa；横向压缩应力最大值分别为-222.75、-218.94、-227.94、-214.86、-221.39、-220.86 MPa。其中，方案四的横向拉伸残余应力值最小，方案三的横向残余应力值最大。

3.1.3 纵向残余应力场分析

进行纵向残余应力分析，给出两种不同方案的横向残余应力所在区域分布云图，列出了六种不同方案的横向残余应力最大值和最小值。如图8和表4所示。

图8 纵向残余应力分布图

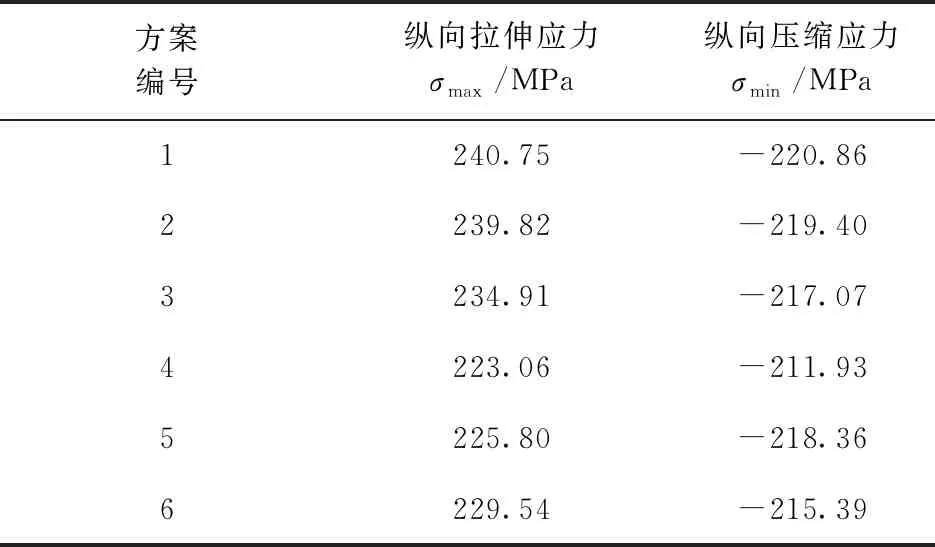
表4 六种方案的纵向残余应力最值

由表4可知，方案一到方案六的纵向拉伸应力最大值分别为240.75、239.82、234.91、223.06、225.80、229.54 MPa，纵向压缩应力最大值分别为-220.86、-219.40、-217.07、-211.93、-218.36、-215.39 MPa。其中，方案四的纵向拉伸残余应力值最小，方案一的纵向拉伸残余应力值最大。

从等效应力、横向残余应力、纵向残余应力三方面来说，方案四的应力值为六种方案中最小，因此方案四的焊接工艺优于其他方案。

3.1.4 局部残余应力分析

为了更加全面的说明方案四残余应力的分布情况，在焊缝处提取一条与焊接平行的曲线来对比六种方案的残余应力，提取路径如图9所示，局部上残余应力各点值的大小如图10～图12所示。

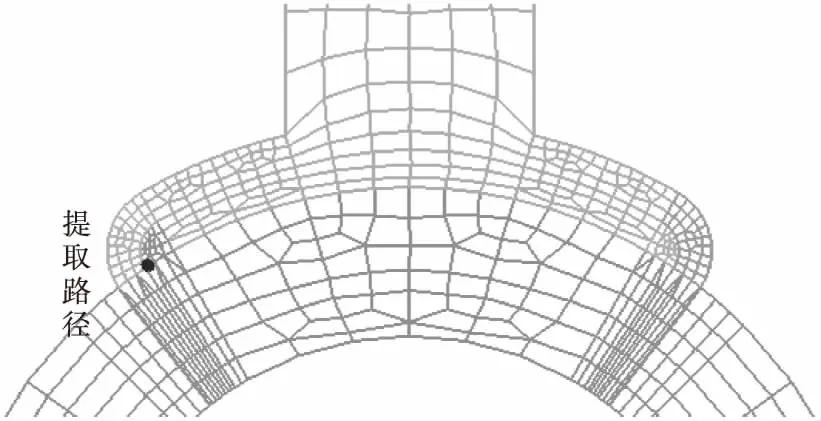
图9 残余应力提取路径图

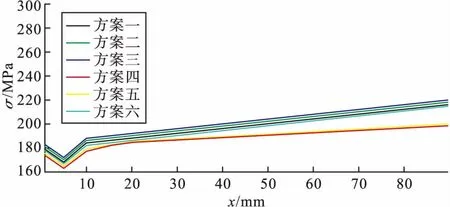
图10 等效应力局部放大图

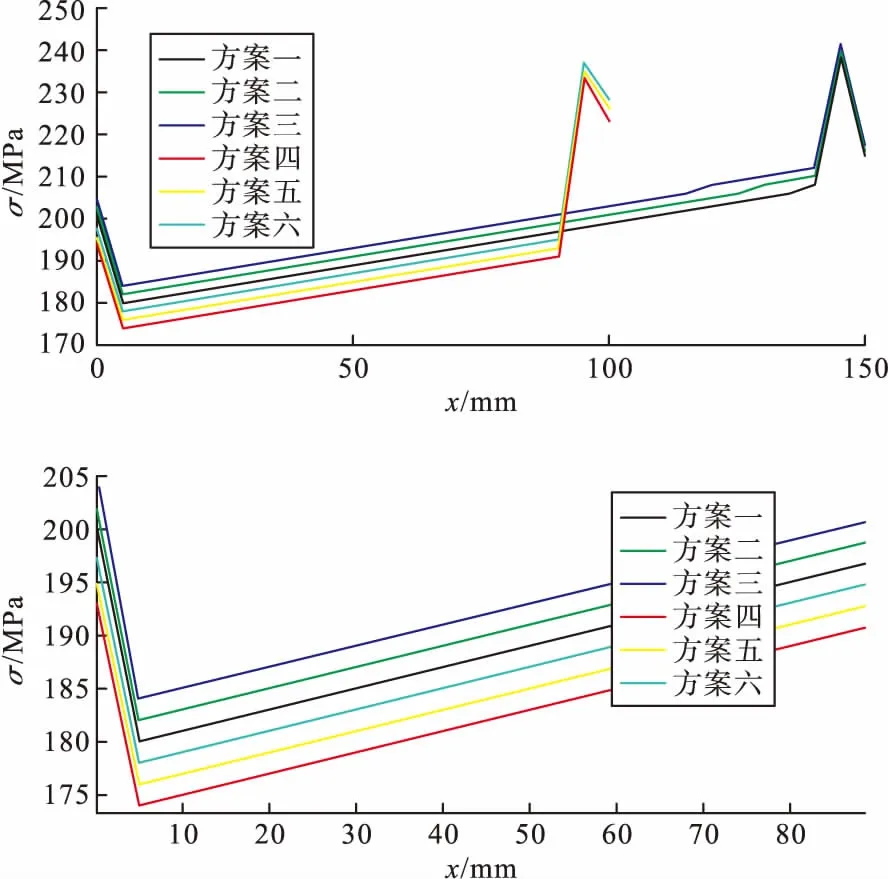
图11 横向残余应力图

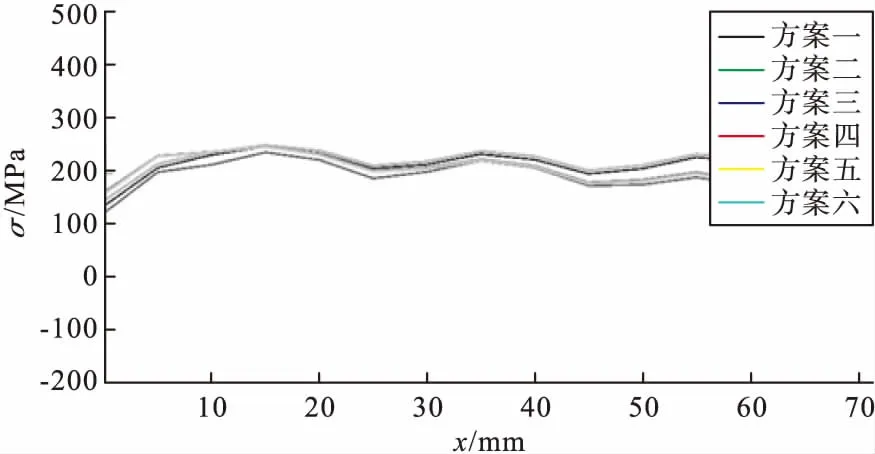
图12 纵向残余应力局部放大图

从图10～图12中知，水梁管道采用方案四的焊接工艺，在同一路径上的等效应力、横向残余应力、纵向残余应力的值在节点上为六种方案里最小，所以方案四能使残余应力最小的首选方案。

3.2 形变场分析

进行轴向形变分析，给出两种不同方案的轴向形变大小所在区域云图，列出了六种不同方案的轴向形变最大值和最小值。如图13和表5所示。

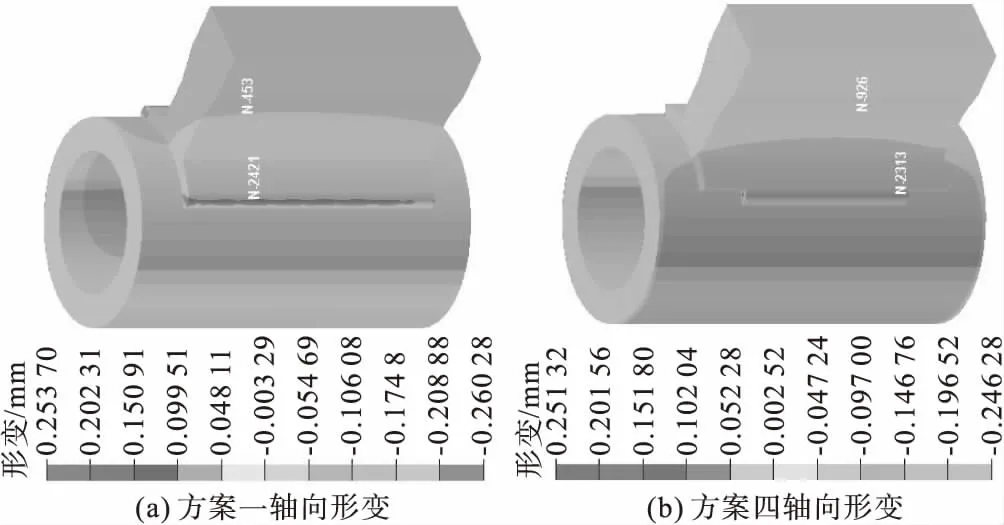
图13 轴向形变云图

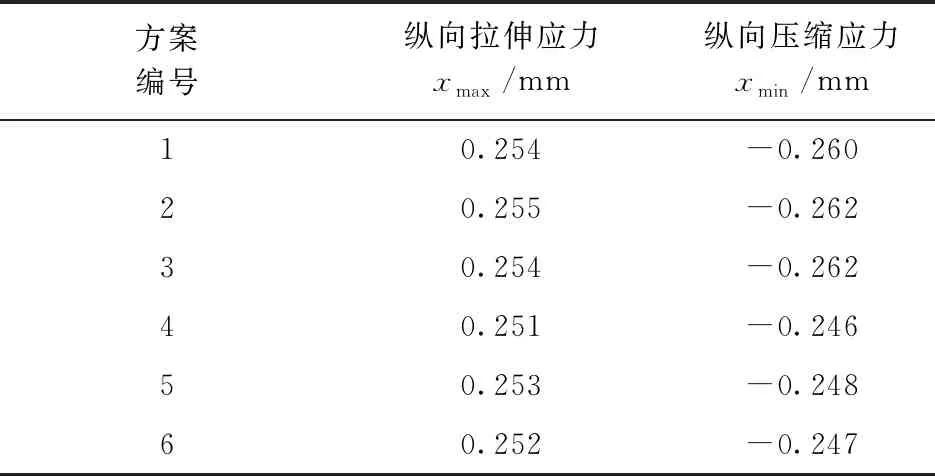
表5 六种方案的轴向形变最值

通过表5可以看出，方案二中横向拉伸形变的最大值为0.255 mm，方案四中有横向拉伸形变的最小值0.251 mm。方案二中横向压缩形变的最大值为-0.262 mm，方案四中横向压缩形变的最小值为-0.246 mm。所以对水梁整个轴向形变而言，方案四为六种方案中最小的一例。

3.3 焊间冷却时间的影响

考虑到焊接完第一道焊缝至第二道焊缝时间开始时，中间的冷却时间长短的因素，有必要进行焊间时间长短对焊接的影响。

3.3.1 等效应力场分析

以图3 中的1→2→3→4焊接顺序为例，给出方案一、方案四的等效应力所在区域分布云图，列出了两种不同方案的焊间冷却时间等效应力最大值和最小值。如图14、图15和表6所示。

图14 方案一

图15 方案四

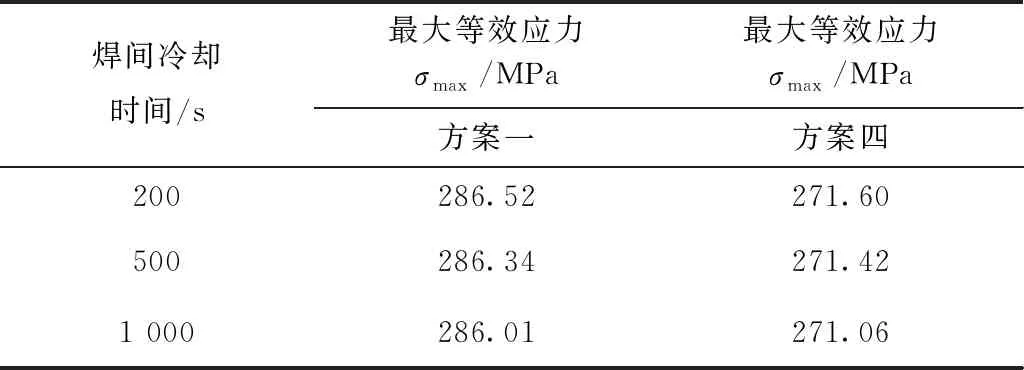
表6 两种方案焊间冷却间隔的等效应力最值

通过表6对比，方案一、方案四在200、500、1 000 s焊间冷却时间中，从等效应力的角度来看，焊间冷却时间长短对于等效应力的影响是极其微小的。

3.3.2 横向残余应力场分析

以图3中的1→2→3→4焊接顺序为例，给出方案一、方案四的横向残余应力云图所在区域，列出了两种不同方案的焊间冷却时间的横向残余应力最大值和最小值。如图16、图17和表7所示。

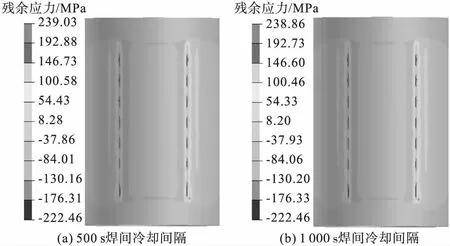
图16 方案一

图17 方案四

由表7可知，方案一、方案四分别在200、500、1 000 s焊间冷却时间中，残余应力变化范围在1 MPa以内，对于横向残余应力的影响是微乎其微的。

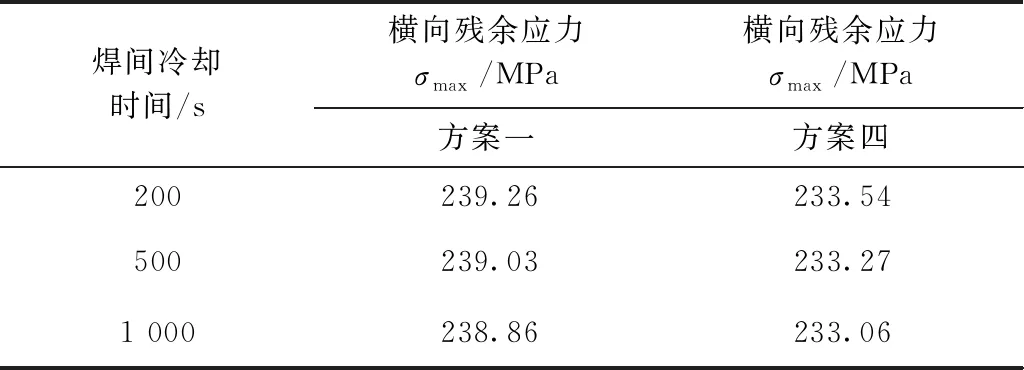
表7 两种方案焊间冷却间隔的横向残余应力最值

3.3.3 纵向残余应力场分析

给出方案一、方案四的横向残余应力云图所在区域，列出两种不同方案的焊间冷却时间的横向残余应力最大值和最小值。如图18、图19和表8所示。

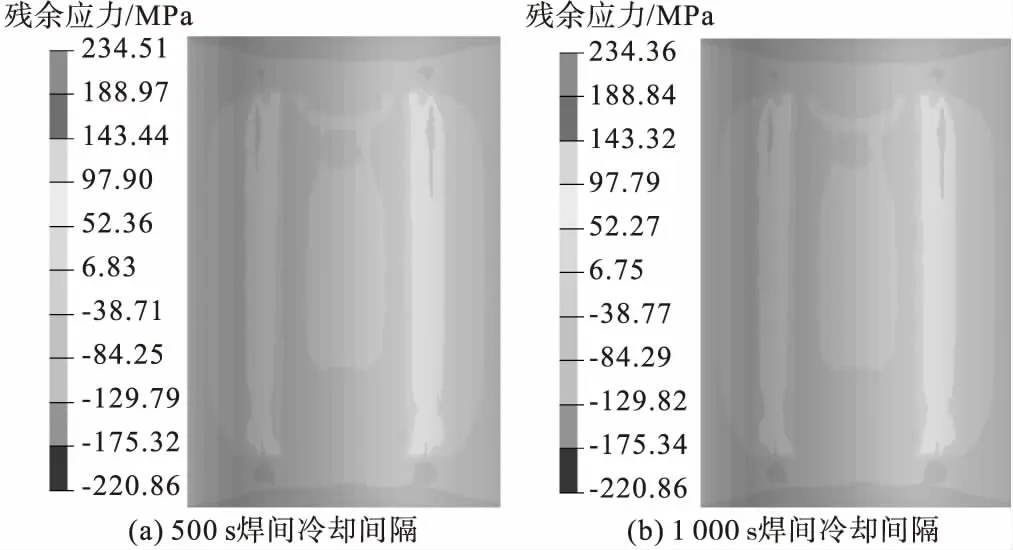
图18 方案一

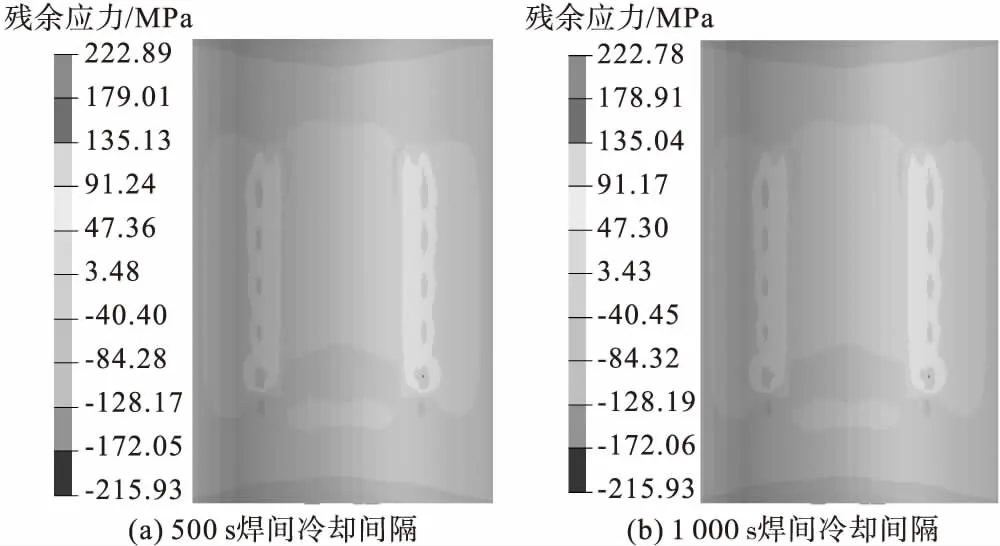
图19 方案四

由表8可知，方案一、方案四分别在200、500、1 000 s焊间冷却时间中，残余应力变化范围在1 MPa以内，对于纵向残余应力的影响是微乎其微的。

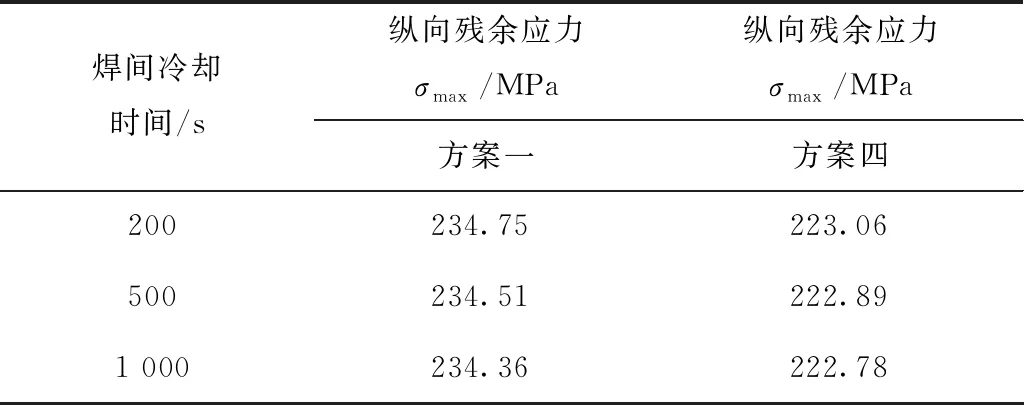
表8 两种方案焊间冷却间隔的纵向残余应力最值

3.3.4 形变场分析

对于形变场采用焊接件的轴向形变进行分析，通过对比焊接件整体轴向形变，来评价焊间冷却时间对焊接效果的影响。以图3中的1→2→3→4焊接顺序为例，给出方案一、和方案四的纵向残余应力云图所在区域，列出了两种不同方案焊间冷却时间的纵向残余应力最大值和最小值如图20、图21和表9所示。

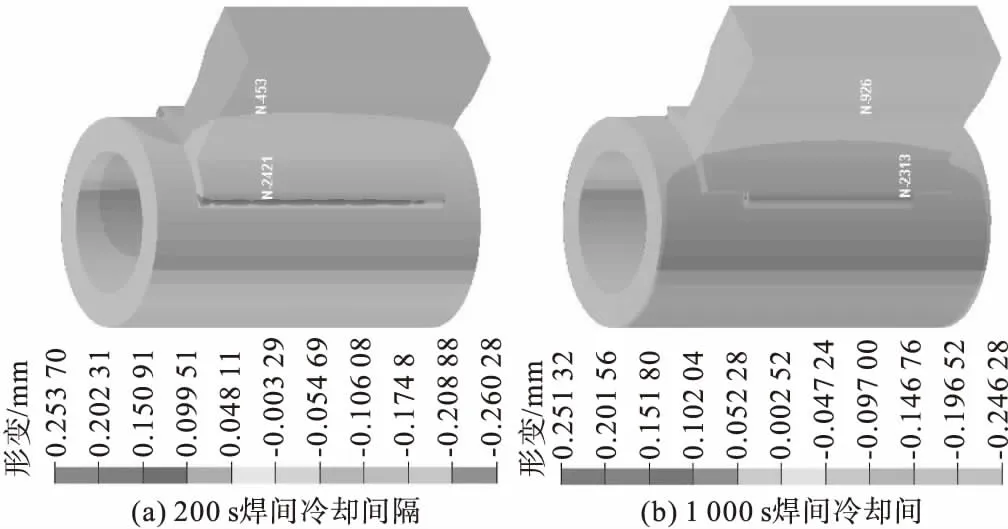
图20 方案一

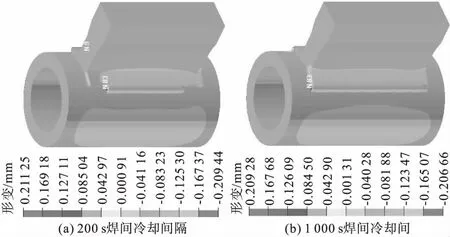
图21 方案四

表9 两种方案焊间冷却间隔的轴向变形值

由表9可知，方案一、方案四在焊间冷却时间分别为200、500、1 000 s焊间冷却时间中，轴向形变的变化也是非常小的。在形变上，焊间冷却时间的长短影响是可以忽略的。

4 结 论

通过数值模拟分析可知：

(1)从焊接模拟结果云图可以看出，焊接产生的残余应力大部分分布在焊缝及焊缝周围处，也验证了水梁最先出现裂纹或者漏水的位置是位于两者焊接端部。

(2)采用六种不同方案的焊接工艺对耐热垫块焊接在水梁结构上进行数值模拟分析，仿真结果对比得出：方案四的焊接顺序(1→2→3→4)且两端留25 mm不焊接时，在等效应力、横向残余应力、纵向残余应力、轴向变形等几个方面上，为几种方案中的最优焊接工艺。

(3)考虑到焊间冷却时间长短的影响，在其他条件不变的情况下，取时间间隔200、500、1 000 s进行数值模拟分析，仿真结果对比得出：在等效应力、横向残余应力、纵向残余应力及形变数据上，确定焊间冷却时间长短对焊接过程影响非常小。