电动汽车驱动系统直流母线稳定性分析*

林 程，孙建侠，徐 垚，易 江

（北京理工大学，电动车辆国家工程实验室，北京 100081）

前言

高压系统是电动汽车的关键系统之一，其主要功能是将储能设备产生的能量转化为不同电压等级和供电形式的电能，提供给车载电气设备使用。电动汽车的高压系统采用高压直流供电架构，多种不同形式和性质的电源/负载集成于高压直流母线上。每个电源/负载都可视为构成系统的基本单元，模块化的设计方法提高了系统的可靠性和冗余度。在一项对美国大型运输机的研究报告中，对高压直流供电系统的供电质量、可靠性、维修性、费用和质量等方面进行了评价，综合评分高达95.8。高压直流供电系统具有明显的技术优势，在中压船舶、多电飞机、直流微网等领域均有广泛应用。

作为衡量高压直流供电系统的唯一性能指标，母线电压的品质直接影响着系统能否正常运行。针对直流母线电压品质的评价，在通信、船舶等直流供电领域已经制定了相关标准。在美国海军的直流电压接口标准MIL−STD−1399中，对直流母线的电压闪变、电压波动、电压偏差、纹波系数以及稳压精度等指标做出了明确要求。这些标准为电动汽车高压直流系统母线电压品质评价提供了参考。目前，国际上对直流系统电压稳定的普遍定义是：在系统受干扰时，直流母线电压波动不超过系统额定值的±10%。

在当前电动汽车高压直流系统集成过程中，各模块往往是单独设计后经过直流母线简单互联，忽略了模块之间的耦合作用。尽管源/载侧模块能够单独稳定工作，集成后的系统却可能发生母线失稳现象，这是因为采用严格闭环控制的电力电子变换器及所带负载具有恒功率特性，而恒功率负载（constant power load，CPL）体现出负阻抗特性，直接导致系统的稳定性降低。当直流母线发生失稳时，母线电压将出现大幅振荡，超出正常波动范围，容易触发电路保护器件动作，严重时甚至导致系统崩溃。通过对某款国产电动客车进行故障数据统计发现其高压系统故障占比达87.88%，远超其他系统故障占比。因此，从系统的角度分析电动汽车高压系统直流母线的稳定性，明确对接入负载的限制条件，并在此基础上研究提高稳定性的方法，对于降低高压系统故障、保证整车安全行驶具有重要的意义。

国内外的学者们对高压直流供电系统稳定性分析方面进行了许多研究。海军工程大学马伟明院士团队对中压船舶直流供电系统的稳定性开展了深入分析，重点研究了发电机系统与推进负载的阻抗匹配问题，通过特征值灵敏度的方法评估了参数变化对系统稳定性的影响，为系统设计提供了依据。天津大学王成山教授课题组对直流微网母线电压的稳定性分析与控制进行了大量研究，分别研究了由电源侧下垂系数设置不当引起的低频电压振荡问题和由CPL负载与LC滤波器级联引起的高频电压振荡问题，并搭建了实验平台进行稳定性分析与控制的验证。北京航空航天大学的周元钧教授开展了对多电飞机高压直流供电系统稳定性的研究，分析了带前端LC滤波器的驱动系统直流母线稳定性问题，并重点研究了LC滤波器及驱动控制器参数对直流母线瞬态特性的影响。加拿大麦克马斯特大学的Ali Emadi教授课题组深入研究了电动汽车高压直流系统的稳定性问题，将电驱动系统等效为CPL负载模型，采用相平面法分析了电源系统带CPL负载时的母线电压稳定性，为源侧变换器设计提供了准则。

现有电动汽车高压直流母线稳定性分析方法中，大多将驱动负载简单等效为恒流源，重点分析源侧变换器对母线电压稳定性的影响。由于等效模型仅在低频域内有效，并不能表征负载的全部频率特性，且在此基础上推导得出的负载限制条件准确度不高。针对这些问题，本文对源侧变换器也进行了等效处理，着重分析了驱动系统负载对母线电压稳定性的影响。采用能够表征负载频率特性的输入导纳模型进行稳定性分析，所得负载限制条件准确度更高。此外，为提高系统稳定性，提出了源/载侧阻抗匹配的调节方法，并结合具体电动汽车实例进行了阻抗匹配设计。最后，通过实车实验验证了所提方案的有效性。

1 高压直流系统

本文研究的电动汽车高压直流系统结构如图1所示，整个系统由电源系统、驱动系统和辅助系统构成。电动汽车的电源系统存在多种不同形式，燃料电池需要经高压DC/DC变换器连接至高压直流母线，蓄电池则通常直连在母线上。单个电源或多个电源复合后连接至高压直流母线，为整车用电设备提供电能。高压直流母线的用电设备包括驱动系统负载和幅值系统负载。其中，驱动系统负载包括DC/AC逆变器、控制器和驱动电机，是电动汽车最主要的系统之一。辅助系统包括辅助电机系统（转向电机、制动电机）、空调系统、低压电源系统、PTC加热器等，用于提高电动汽车的操纵性和舒适性。

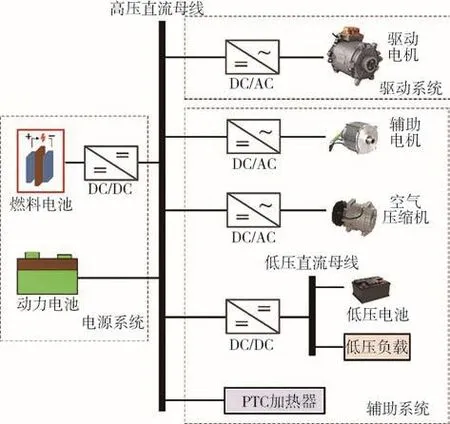
图1 电动汽车高压直流系统结构

2 阻抗模型

2.1 系统传递函数模型

图1所示的高压直流系统是一个复杂的非线性系统，直接对其进行稳定性研究不仅十分困难，也不利于发掘稳定性作用机理。因此，本文采用小信号稳定分析法，通过对系统稳态工作点进行线性化处理，降低高压直流系统的非线性度，在此基础上进行稳定性分析，为实际系统的稳定运行提供理论依据。

由美国加州理工学院Middlebrook教授提出的阻抗分析法被广泛应用于直流系统的小信号稳定性分析中。整个高压直流系统可以分为电源和负载两个部分，等效电路如图2所示。直流母线电压的传递函数可以表示为

图2 系统等效电路图

式中：与为电源电压与母线电压的小信号分量；为源侧输出阻抗；为载侧输入导纳。上式中代表源侧与载侧系统的阻抗比，反映了两个子系统之间的影响。

此外，由式（1）可以看出为直流母线电压的开环传递函数。根据Nyquist判据，为使系统稳定，在复平面的Nyquist曲线应不包围（−1，j0）点。因此，Middlebrook教授提出若的幅值在整个频域范围内均小于1，则系统一定符合Nyqsuit稳定判据 的 要 求，这 就 是 著 名 的 Middlebrook 稳 定判据。

2.2 源侧输出阻抗

直流电源经过高压DC/DC变换器连接至高压直流母线的电路结构如图3所示，图中，、、分别表示DC/DC变换器的电阻、电感、电容，为DC/DC变换器占空比，、分别为电源电压和母线电压，、分别为变换器输入和输出电流。

图3 电源系统等效电路图

根据电路原理建立如下高压DC/DC变换器的状态空间模型：

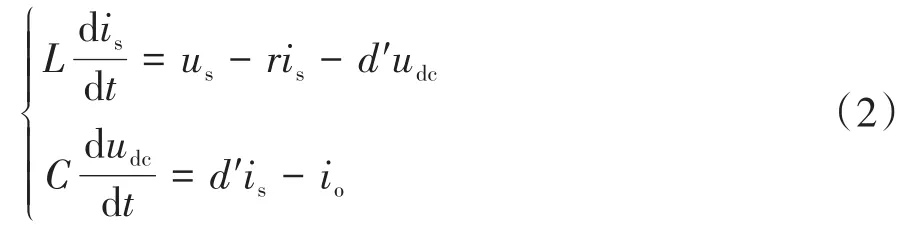
其中′=1−

根据文献［23］所述DC/DC变换器建模方法，对式（2）进行小信号处理，得到小信号模型：

式中：前缀“”表示变量的小信号扰动；′=1−，为DC/DC变换器占空比稳态值；、分别为、的稳态值。

忽略电源及占空比扰动，令=0，=0，根据式（3）可以得到源侧高压DC/DC变换器的开环输出阻抗为

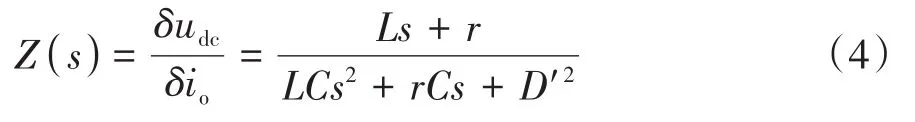
由上式可以看出，在谐振频率处达到谐振幅值，容易超过系统稳定判据的限制。于是，此频段也被称为易失稳区。根据文献［24］中的分析结果，DC/DC变换器引入闭环控制后，能够抑制输出阻抗在谐振频率处的幅值尖峰，提高系统稳定性。由此可以看出，若开环系统满足系统稳定判据要求，则闭环系统也一定满足稳定性要求。因此，本文将根据稳定性更为苛刻的开环输出阻抗模型进行稳定性分析。

对于并联在直流母线上的蓄电池组可以等效为理想电源串联电阻和电容的Thevenin模型，为简化模型复杂程度，忽略电池内阻的影响，将蓄电池的输出阻抗等效为电容。将所有并联在高压直流母线上的电容器包括蓄电池等效电容、负载逆变器直流支撑电容合并为一个电容器，与高压DC/DC变换器的输出阻抗并联后，可以得到电源系统的输出阻抗为

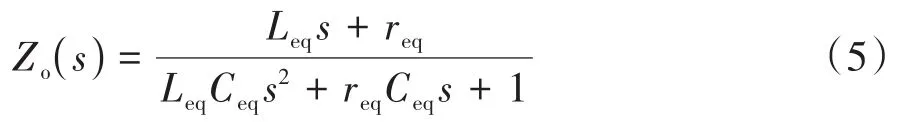
式中、、表示等效电阻、电感与电容，且有=/′，=/′，=+。

2.3 载侧输入导纳

电动汽车的高压直流母线与多种不同性质的负载相连，其中驱动系统的功率占比远高于其余辅助系统的功率占比，是影响高压直流母线稳定性最主要的因素。因此，本文将重点分析驱动系统负载对高压母线稳定性的影响。整个驱动系统的电路拓扑结构如图4所示，逆变器采用三相电压型逆变器，驱动电机采用永磁同步电机（permanent magnet synchronous motor，PMSM），控制器采用磁场定向矢量控制（field−oriented control，FOC）策略，采集电机转速、交流电流及母线电压等信息，并根据给定信号输出PWM开关调制信号控制逆变器实现电机调速控制。

图4 驱动系统的整体框图

驱动系统包含了许多不同时间尺度的变量，如图5所示。对于这样时间尺度跨度大的系统，其全系统详细数学模型十分复杂，难以用于稳定性分析研究。因此，本文以电磁时间尺度作为建模基础，将机电时间尺度和中长期时间尺度的变量均看作恒定值，忽略其动态变化的影响。在此基础上，根据文献［26］中所示建模方法推导得到驱动系统的输入导纳模型。

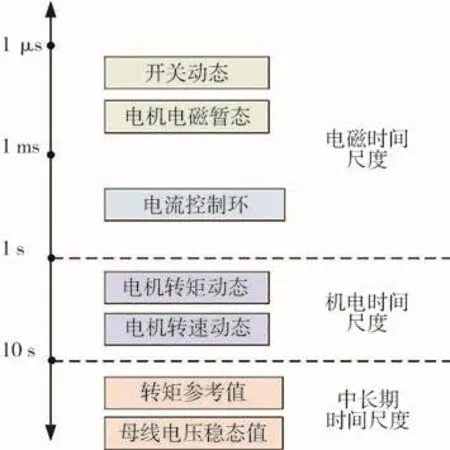
图5 驱动系统时间尺度示意图

根据功率平衡原理，在忽略逆变器的功率损耗时，有

式中：、分别为母线电压与电流；u、u分别为轴定子电压；i、i分别为轴定子电流。

根据小信号分析法对上式进行化简，可以求得输入导纳为

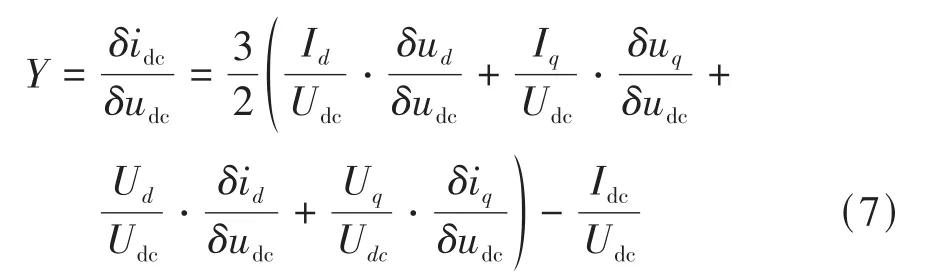
式中：I、I为i、i的稳态工作点；U、U为u、u的稳态工作点；、为、的稳态工作点。前缀“”表示对应变量的小信号扰动。

根据驱动系统各模块的工作原理及数学关系可以建立整个系统的小信号模型，如图6所示，图中D、D为轴逆变器占空比稳态值，为定子电阻，L、L为轴电感，为永磁体磁链，为电机电角速度，表示电流环PI调节器，且有=+K/s，、分别为比例和积分系数。根据图示数学关系，可以求得

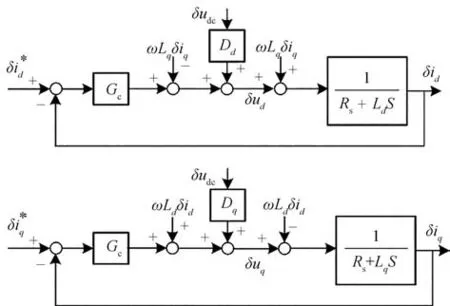
图6 驱动系统小信号模型

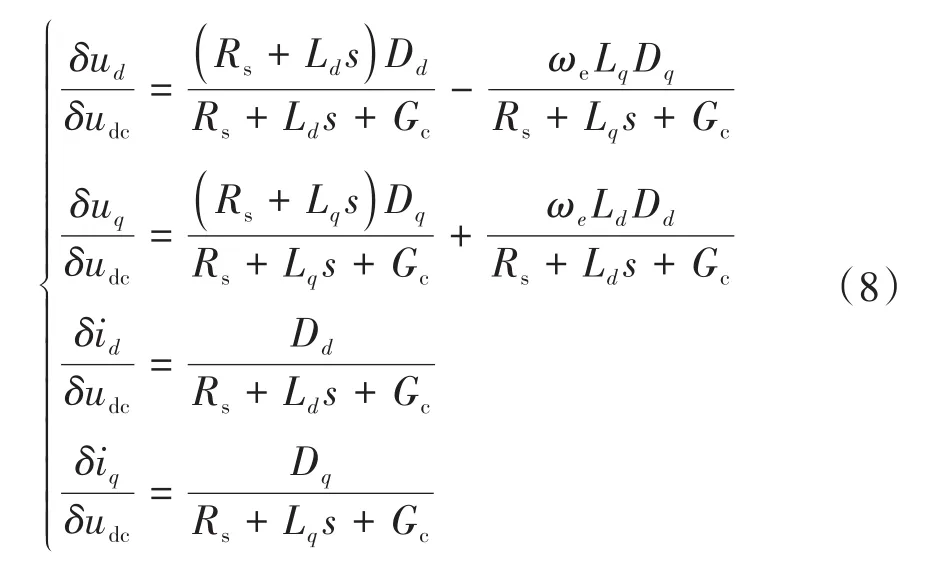
将式（8）代入式（7）中可以求得驱动系统的输入导纳为

式中为负载功率，=。

可以看出包含两个部分，等号右侧第一项表示轴导纳Y，第二项表示轴导纳Y。可以看出Y具有负导纳特性，Y为正导纳。Y的存在能够使驱动系统的负阻抗特性减弱，系统稳定性提高。驱动电机为表贴式PMSM时，轴导纳Y为0，系统输入导纳=Y，稳定性要更加苛刻。因此，本文以表贴式PMSM模型为基础进行稳定性分析，此时驱动系统输入导纳可以简化为

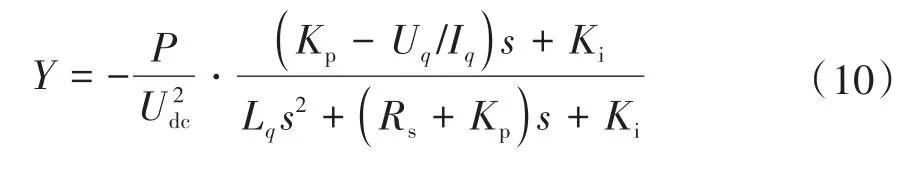
3 稳定性分析

源侧输出阻抗与载侧输入导纳的频率特性曲线如图7所示，其中ω为的谐振频率，ω为的转折频率：

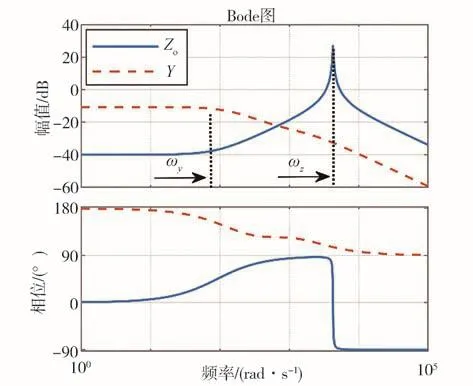
图7 Z o与Y频率特性曲线

的带宽接近电流内环的带宽，通常在几十至几百Hz，远小于源侧阻抗的谐振频率，即有ω<<ω。由图7可以看出，在ω频率处达到谐振幅值，且的谐振幅值为

在ω频率处达到谐振幅值，且的谐振幅值为

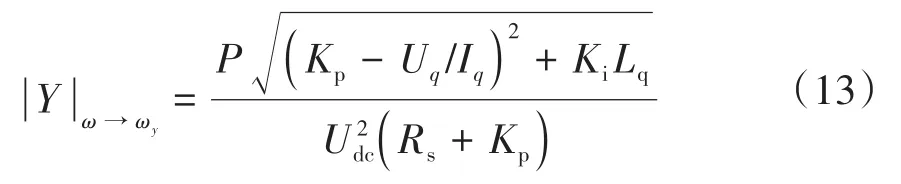
根据Middlebrook稳定判据的要求，阻抗比的幅值应始终小于1。由于的幅值不超过与谐振幅值的乘积，即有

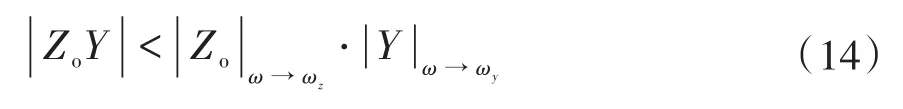
因此，通过令与谐振幅值的乘积小于1，即可使系统满足稳定性要求。将式（12）和式（13）代入式（14）中化简可以得到系统稳定条件：

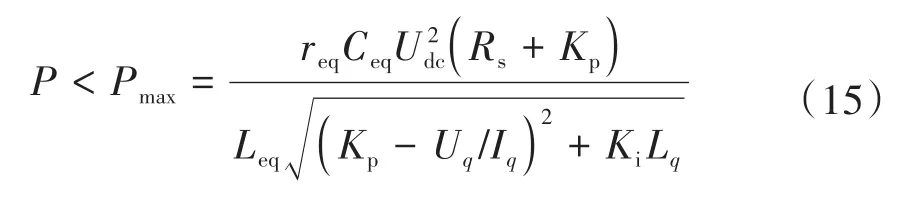
式中表示直流母线准入的负载功率限制。

上述稳定条件对接入直流母线的驱动系统功率提出了限制要求。负载功率满足稳定条件时，直流母线电压能保持稳定，负载功率超过限制时容易造成母线电压振荡问题。

根据之前的分析可以看出母线电压系统稳定性与源载侧阻抗比有关，通过合理地配置源/载侧阻抗，减小的幅值，可以增加系统稳定裕量，提高母线电压品质。阻抗匹配可以通过降低源侧阻抗幅值或降低载侧导纳幅值来实现。其中，源侧阻抗与硬件阻尼有关，通过降低电感值、提高电阻值和电容值等方法可以降低的谐振幅值，如图8所示。载侧导纳与母线电压、电机硬件及控制器等参数有关，电机硬件在设备选型时已经确定。提高母线电压等级可以降低的负阻抗特性，减小整个频域内的幅值，如图9所示。根据式（10）可以看出，的值直接影响在中高频段的幅值，当的值接近U/I时，可以降低在中高频段的幅值，如图10所示。因此，提高系统稳定裕量的方法包括：（1）提高源侧阻尼；（2）提高母线电压等级；（3）合理配置载侧控制器PI参数。

图8 电容增加时源侧阻抗幅值变化

图9 母线电压增加时载侧导纳幅值变化

图10 K p接近Uq/Iq时源载侧幅值变化

4 实验验证

本节将结合具体电动汽车实例进行稳定性分析，根据实车工况数据验证前述分析结论。电动汽车高压直流系统的直流电源为燃料电池，输出电压为150 V。燃料电池经高压DC/DC变换器后连接至高压直流母线，输出功率为40 kW。高压DC/DC变换器采用双向DC/DC变换器，其开关频率为80 kHz。此外，为提高直流母线电压品质，母线上并联蓄电池组，容量为96 A·h，标称电压为627.6 V。驱动系统采用三相电压源型逆变器，开关频率为10 kHz。驱动电机为PMSM，额定转矩为550 N·m，峰值转速为4 500 r/min，额定功率为110 kW，峰值功率为175 kW。高压直流系统各个模块的参数设置详见表1。

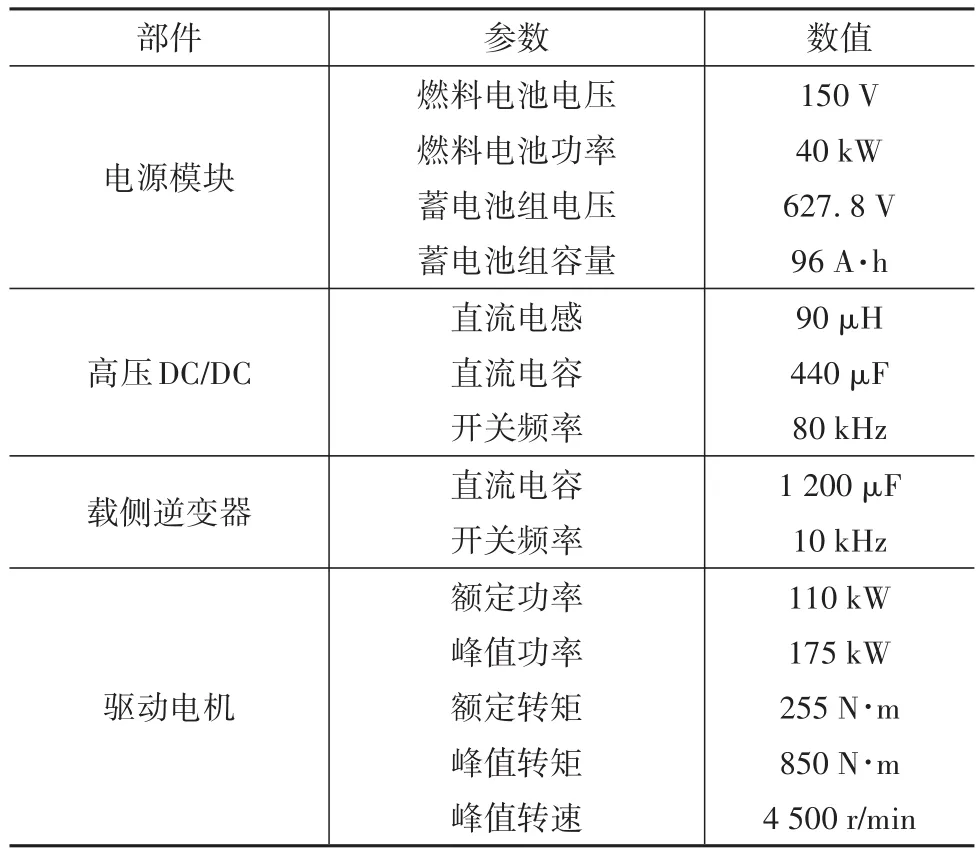
表1 高压直流系统参数

根据式（15）和表1所示参数，得出负载实际运行功率与限制功率的关系，如图11所示。可以看出，电机运行功率始终小于限制功率，母线电压能够保证稳定。为了验证所述分析结论，进行了实车验证。电动汽车行驶在延庆区的盘山公路，行驶工况包括连续弯道、上下坡等山区工况。燃料电池、蓄电池组及驱动负载功率变化如图12（a）所示，在实车运行过程中，燃料电池提供恒定输出功率，蓄电池组根据驱动系统的功率需求提供波动功率，能够起到削峰填谷作用，抑制负载功率变化对母线电压的冲击。

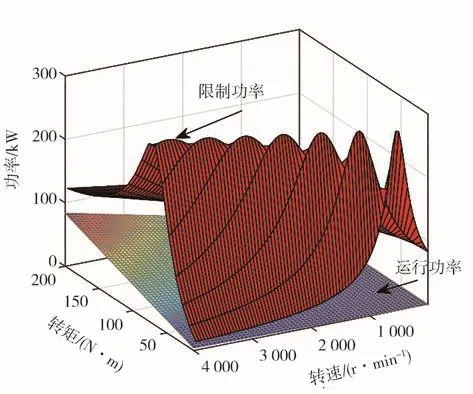
图11 负载限制功率与实际运行功率关系

图12（b）所示为母线电压波形，母线电压最大值为654.2 V，最小值为635.4 V，母线电压波动为18.8 V。根据直流电压接口标准MIL−STD−1399的要求，稳态时母线电压波动应小于±4%，因此，高压母线电压波动应小于25.6 V。可以看出，图12（b）所示电压波动符合标准要求，母线电压稳定。

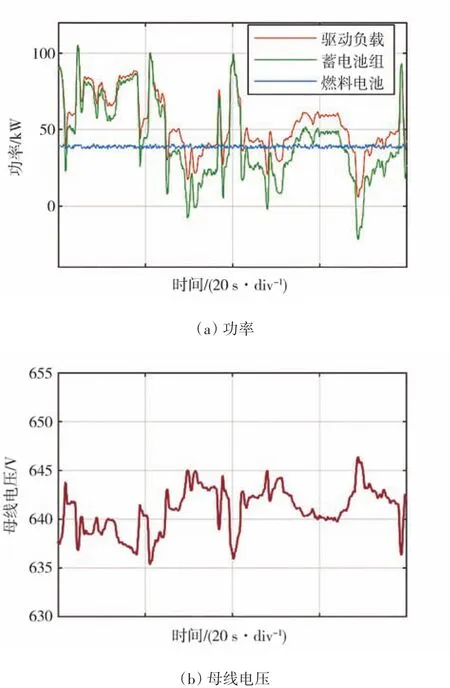
图12 实车测量结果

5 结论

本文基于系统阻抗模型推导了直流母线电压全频域稳定条件，并由此对负载功率提出了限制要求。阻抗模型能够描述负载的频率特性，因此所得稳定条件能够保证母线电压在整个频域范围内的稳定性，准确度更高。通过源/载侧阻抗匹配可以提高母线电压品质，方法包括：（1）提高源侧阻尼；（2）提高母线电压等级；（3）合理配置载侧控制器PI参数。稳定性分析结论通过具体实例得到了验证，为系统的硬件和控制器参数设计提供了参考依据，有助于改善和提升高压系统的稳定性能。