计及出租车充电行为的微电网能量管理研究*

陈 宇，吴晓刚，杜玖玉，孙金磊

（1.哈尔滨理工大学电气与电子工程学院，哈尔滨 150006；2.清华大学，汽车安全与节能国家重点实验室，北京 100084；3.南京理工大学自动化学院，南京 210094）

前言

为解决日益突出的能源危机和环境污染问题，面向碳中和的低碳、零碳乃至负碳技术将成为未来全球产业革命和科技竞争的关键。因此，光伏、风力等各种可再生能源发电在微电网中的渗入率逐年增加，电动汽车同时作为负载和移动储能装置，与微电网的融合和协同控制也成为研究的热点。

光伏发电受到环境等因素影响具有很大的不确定性，电动汽车与电网之间的充放电行为也具有一定的随机性，如果不能对其进行合理的管理与控制，可能造成峰值负荷增加、电能质量降低和切负荷量增加等一系列问题，从而对微电网的经济和稳定运行产生重大影响。经济性与稳定性是微电网建设中需要考虑的重要因素，通常根据可利用的能源情况和电网负荷要求，以经济性或供电可靠性等最优为目标进行优化，确定微电网中分布式电源的类型、容量，并保证电网运行的稳定性，在此基础上，进行微电网经济性调度和运行。

在微电网经济性调度研究方面，文献［5］中以成本最低为目标，利用混合粒子群优化算法在发电机组之间获得最优经济发电计划，最终提高微电网的可调度性，降低微电网的运行成本。文献［6］中提出了一种改进的帝企鹅优化算法，在已投入运行的发电系统中寻找发电的经济调度，解决基于化石燃料和可再生能源系统的动态经济调度问题。文献［7］中建立了用于电动汽车、可转移负荷和其他分布式发电的微电网经济调度的多目标模型，并研究了电动汽车充放电行为和需求侧响应对光伏并网系统经济运行的影响。文献［8］中针对可再生能源和电动汽车充电的不确定性，利用不确定成本函数的1阶导数和2阶导数进行数学分析，构建了太阳能光伏发电、风力发电、插电式电动汽车和径向水轮发电机的边界不确定成本函数。文献［9］中提出了以微电网系统效益最大化为目标函数的分布式优化策略，储能系统可根据历史平均结算价格和充电成本价格实时调整充放电状态，同时处理平衡和不平衡约束，随时保证电力供需平衡。

在微电网结构与运行策略的研究方面，文献［10］和文献［11］中提出了储能系统的运行策略，以解决光伏发电引起的功率变化和局部负荷波动问题。并以经济性为目标，制定了微网发电各部件、负荷和储能电池之间的优化调度计划。文献［12］中考虑了可转移负荷对用户满意度的影响和可再生能源跟踪负荷的能力，提出了热电耦合微电网的最优调度策略。文献［13］中提出了一种双层家庭微电网能量管理系统，上层使用模型预测的方法对家庭用电负荷分布进行优化，下层采用实时控制器确定储能系统最优功率的输入输出，降低了家庭日常能源成本的同时将光伏利用最大化。文献［14］中提出了一种适用于工业微电网的能量管理系统，一方面考虑电池储能成本来确定最优储能规模，另一方面研究了考虑储能效率、充放电速率等各种运行极限的微网运行成本问题，并根据随机情景来解决不确定性。文献［15］中基于使用负荷剖面和发电资源预测的功率提出了一种能量管理策略，以促进微电网中的电力分配，提高微电网在现有电网中的可靠性、控制水平和渗透率，并考虑了电网波动的稳定性。文献［16］和文献［17］中考虑了社区微电网与电网的互联，使用储能系统作为调节，通过出售多余的可再生能源获得最大利润，同时使成本最小化以满足微电网的负荷需求。

综上，在可再生能源构建的微电网系统运行控制的研究方面，大部分围绕微电网的结构、算法和策略进行研究。少有从微电网的经济性和稳定性需求，优化电动汽车的充电规则的报道。本文中以哈尔滨市出租车出行特征和运行工况作为背景，将出租车空驶率、负荷稳定性和系统经济性研究相结合，对电动出租车的充电规则进行了优化。

1 直流微电网结构与各分布式电源模型

1.1 直流微电网结构与调度规则

图1为所研究的直流微电网系统的结构，主要包括发电部分（光伏发电、燃气轮机发电、燃料电池发电）和负荷部分（出租车、本地负荷、储能电池），各部分分别通过电力电子变换器接入直流母线。

图1 直流微电网系统结构图

根据光伏发电和电动出租车的实际工况调整燃气轮机、燃料电池等发电环节的发电情况，利用储能系统实现微电网的辅助控制，从而达到系统功率平衡的目的，在调整过程中优先考虑系统的可靠性和经济性。整个系统的调度规则为：

（1）光伏发电单元由于具有可再生和清洁特性，被作为主力电源优先输出；

（2）燃气轮机和燃料电池具有灵活的可调度性，因此它们在系统负荷量过大导致光伏发电供给不足时工作；

（3）储能电池在系统发电量富余时充当负荷来储存能量，在系统发电量不足时又可作为后备电源发电。

1.2 分布式电源成本计算模型

1.2.1 光伏发电成本模型

光伏（photovoltaic，PV）将光能直接转化为电能。参照文献［18］中的光伏发电模型，将光伏发电量与光照强度和温度的关系拟合得到24 h内光伏发电单元的发电功率数学模型：

光伏电池发电功率为

式中：为光伏电池发电功率，W；为光照强度，W/m；为标准测试条件下（光照强度为1 000 W/m，环境温度为25℃）的最大测试功率，W；为标准测试条件下的光照强度，其值取1 000 W/m；为功率温度系数，℃；为电池板工作温度，℃；为参考温度，℃。

光伏发电的运行成本为

式中：表示 PV的运行管理成本，元；为PV的运行维护成本系数，元/（W·s）；为时间间隔数；Δ为时间间隔，s；（）为第时刻PV输出功率，W。

1.2.2 燃气轮机成本模型

燃气轮机（gas turbine，GT）主要考虑其运行管理成本和燃料成本两部分，即

式中：表示 GT 的运行管理成本，元；为GT的运行维护成本系数，元/（W·s）；（）为第时刻 GT 发电功率，W；为 GT 的燃料成本，元；为天然气的低热值，J/m；为 GT 的燃料气体天然气单价，元/m；为GT的发电效率。

1.2.3 燃料电池成本模型

燃料电池（fuel cell，FC）使用成本主要可分为运行管理成本和燃料成本两部分，即

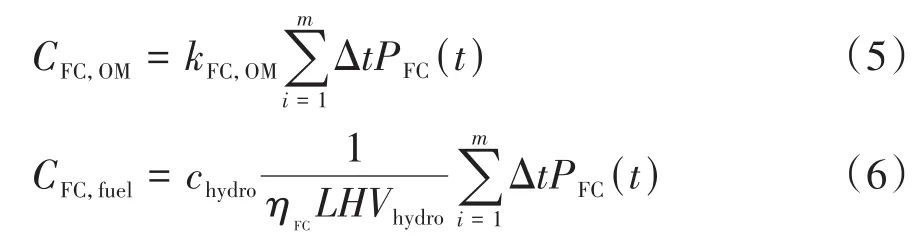
式中：表示 FC 的运行管理成本，元；为FC的运行维护成本系数，元/（W·s）；（）为第时刻 FC 发电功率，W；为 FC 的燃料成本，元；为氢气的低热值，J/m；为 FC的燃料气体氢气单价，元/m；为FC的发电效率。

1.2.4 储能电池成本模型

本文中电池储能系统（energy storage，ES）的电能是光伏发电储存得到的，故其使用成本主要是运行管理成本：

式中：SOC（）为时刻 ES 荷电状态；和分别为ES的充电和放电效率；为额定功率；表示 ES的运行管理成本；为ES的运行维护成本系数；（）为第时刻ES输出功率。

2 出租车充电场景的设定

2.1 基于出租车出行特征的充电场景设定

利用GPS对哈尔滨出租车出行特征数据进行调研与分析，图2为哈尔滨市出租车在不同时间段内的空驶率（出租车在正常运行时，空载的里程或时间占行驶的总里程或时间的比例）分布特点。

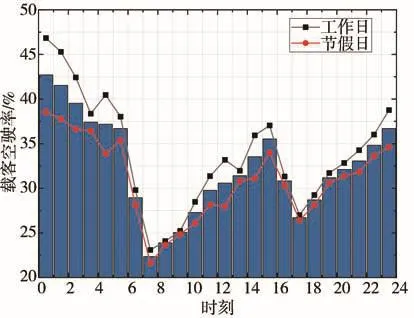
图2 哈尔滨市出租车载客空驶率分布

由图2可以看出，哈尔滨出租车载客空驶率通常在20%~50%之间，工作日比节假日的总空驶率略高，但在时间分布上没有明显的差异。本文选取节假日与工作日的平均载客空驶率进行分析。晚上22点至凌晨6点时出租车平均载客空驶率为38.9%，中午12点至下午17点时出租车平均载客空驶率为31.938%，这两个时间段是出租车载客空驶率相对较高的两个时间段。

根据哈尔滨市出租车出行特点和出租车公司轮班制度，设置以下几种可能出现的电动出租车充电场景。

场景一：晚上空驶率开始上升时直接下班，对电动出租车进行充电。

场景二：晚上空驶率升高一段时间后，再下班进行充电，白天驾驶员交接班时再进行一次充电。

场景三：以最小化出租车空载率为目标进行充电，当空载率高于设定值时，安排电量低的出租车充电。

2.2 基于微电网负荷稳定性的充电场景设定

某住宅区用户日用电功率统计数据如图3所示。日用电功率集中在70~150 kW之间，负荷谷值出现在1点至5点与下午12点至14点两个时间段。

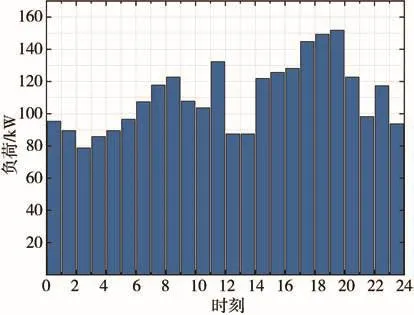
图3 住宅用电负荷分布

由此设定出租车充电场景四，即以优先安排在负荷曲线的谷底时段进行充电为原则，当住宅在线负荷低于设定阈值时，未载客出租车可进行充电。

2.3 综合优化充电场景设定

在用电低峰期调配出租车去充电，可能会影响人们的出行，因此本文提出了综合考虑负荷稳定性与出租车出行特征的充电场景。结合哈尔滨市出租车载客空驶率分布曲线、住宅负荷分布曲线和光伏发电分布曲线，综合进行策略优化计算，优先安排在用户用车需求低且空驶率高的时段进行充电，由此设置出租车充电场景五，即同时设定住宅在线负荷阈值与出租车载客空驶率阈值，在满足两个约束条件下才可进行充电。

2.4 无序充电场景设定

在微电网能量管理系统出现问题时，可能会出现网内出租车无法进行有序充电的情况。因此须明晰这种情况下的各分布式电源的发电情况和系统成本，由此设置出租车充电场景六。根据文献［21］，电动汽车充电起始SOC呈现正态分布，因此本文对电动出租车充电起始时间不做约束，充电起始SOC在（0.2，0.8）内采用normrnd函数在正态分布中生成随机数，即

起始充电时间为

起始充电能量状态为随机函数为

2.5 无经济性优化充电场景设定

基于以上6个充电场景，设置确定的约束阈值，进行不涉及经济性优化的案例仿真，具体参数设置如图4所示。

图4 不同场景下充电阈值的设置

在对微电网系统中各分布式电源不进行以经济性为目标的优化求解时，须提前设定好各分布式电源的发电顺序，从环境友好性和经济性角度出发，配置各分布式电源的发电顺序为光伏发电、燃气轮机发电、燃料电池发电和储能电池发电。

3 直流微电网能量管理优化方法

在已建立的微电网最优经济运行模型的基础上，根据负荷、光伏功率和6种充电场景下的出租车充电负荷，对微电网未来24 h的分布式电源输出进行优化。采用蒙特卡洛（MC）方法实现对未来出租车负荷分布的预测，同时利用粒子群优化算法求解模型，如图5所示。

图5 微电网经济调度模型

3.1 目标函数与约束条件的制定

以微电网总发电成本最优为目标，建立考虑可再生能源发电不确定性的孤岛型微电网经济调度模型，即目标函数为

微电网在制定调度计划时，应满足安全、可靠的运行条件，因此各单元应满足以下约束条件。

①储能电池充放电约束：

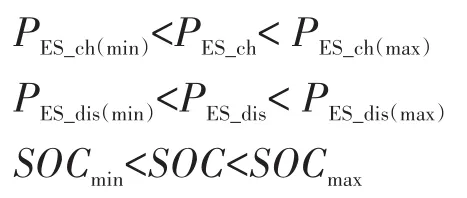
②燃气轮机约束：<<

③燃料电池约束：<<

④功率平衡约束：+++=+式中和分别为出租车充电功率和住宅用电功率。

3.2 出租车充电负荷预测

根据不同充电场景下出租车充电起始时间和充电起始SOC约束，计算产生的充电负荷和需要的充电时长，结合出租车相关参数，设置100次蒙特卡罗算法对出租车有序充放电负荷进行预测，过程如图6所示。

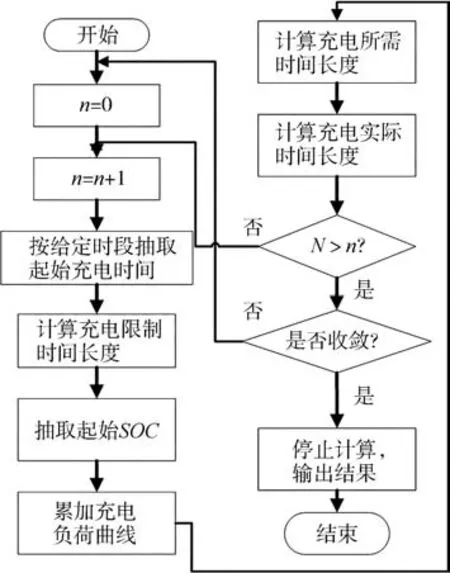
图6 出租车负荷预测算法流程图

3.3 基于粒子群优化算法的直流微电网能量管理优化

粒子群算法的目标是使所有粒子在多维超体（multi−dimensional hyper−volume）中找到最优解，如图7所示。本文将所建立的微电网经济调度模型采用粒子群算法进行求解。

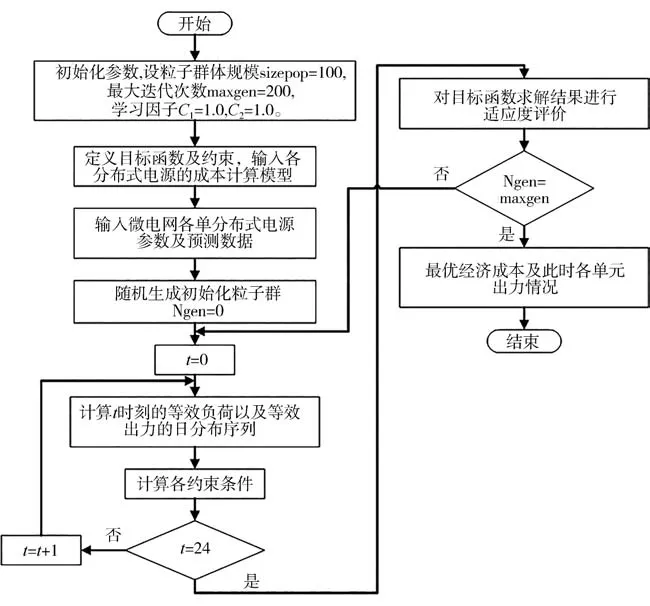
图7 应用粒子群算法的模型求解过程

首先输入各分布式电源参数，设置HPSO参数，初始化粒子的位置和速度，产生初始粒子群；再根据分布式电源产生的输出和负载，调整分布式电源功率和储能系统，以满足负载平衡和输出的约束；以目标函数作为适应度值，更新粒子的速度和位置，同时根据计算出的适应值更新最优个体粒子和最优全局粒子，执行交叉和变异操作，个体最优交叉的新粒子通过个体最优粒子的交叉获得，通过个体最优粒子和全局最优粒子的交叉，得到全局最优交叉的新粒子；判断迭代次数Ngen是否达到预设数量maxgen，若未达到，则进入下一步迭代，若达到，则结束循环迭代，输出全局最优和最优粒子位置，即在调度期间微型资源和能量存储系统的最优经济成本和输出。

4 仿真与结果分析

针对出租车充电行为不确定性问题共设置6种充电场景。在此基础上，对每种充电策略优化前后的出租车空载率、在线负荷峰谷差率和微电网系统运行总成本进行对比。

4.1 仿真参数设定

选取哈尔滨市某办公区的微电网数据进行仿真求解和分析，该算例的微电网中包括容量上限为100 kW的光伏电池，容量上限为150 kW的微型燃气轮机，容量上限为100 kW的燃料电池和容量上限为100 kW·h的储能电池；同一车型的电动出租车20辆，平均行驶速度为30 km/h，具体参数如表1所示。

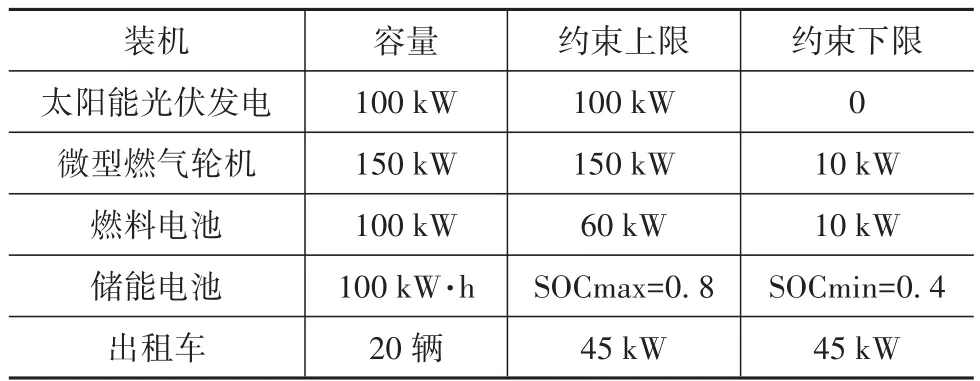
表1 微电网系统各单元基本参数

其中，基于历史数据的光伏发电分布如图8所示，光伏发电数据来自于晴天条件下的光照强度与温度数据的统计采用式（1）计算而得。

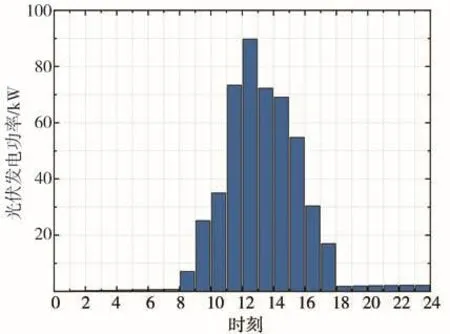
图8 光伏发电功率分布

采用蒙特卡洛算法，分别针对以上6种充电场景下出租车产生的负荷进行预测，结果如图9所示。

图9 基于MC算法的出租车负荷分布

4.2 不考虑经济性优化的微电网各分布式电源发电分配

根据住宅用电负荷、光伏发电曲线，结合不考虑经济性优化电动出租车充电场景一至六，对微电网内分布式电源未来24 h的发电情况进行分配，各分布式电源的发电计划如图10所示。将各分布式电源发电情况代回成本计算模型中，算得调度期间系统运行总成本，如表2所示。

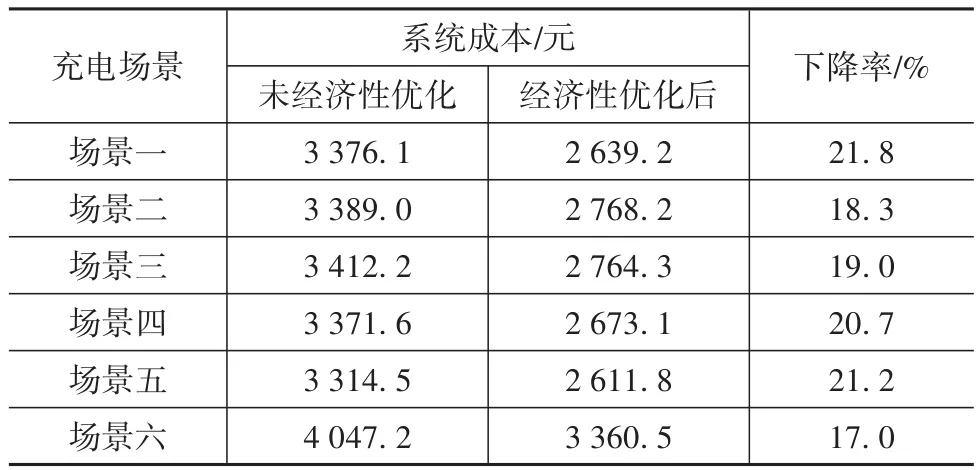
表2 经济性优化前后不同充电场景系统成本的对比

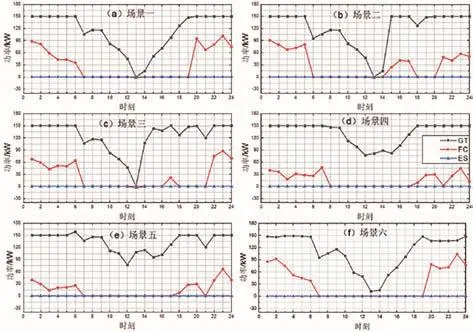
图10 无优化条件下不同充电场景的分布式电源发电情况

由图10和表2可以看出，在不考虑经济性优化时，各充电场景下的分布式电源发电情况相似。燃气轮机长期工作在满载状态，一方面会缩短设备使用寿命，另一方面很大程度上增加了运维成本。同时，燃料电池起到电量补充的效果，而储能电池基本不发挥任何作用。无序充电的场景六的系统总成本比前5种充电场景都高。

4.3 考虑经济性优化的微电网各分布式电源发电分配

根据住宅用电量、光伏发电曲线，结合考虑经济性优化电动出租车充电场景一至六，对微电网内分布式电源未来24 h的发电情况进行分配，各分布式电源的发电计划如图11~图14所示。下面对各场景下的优化结果进行具体分析。

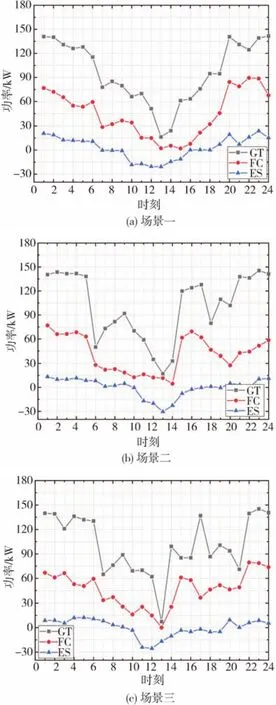
图11 场景一、二、三下考虑经济性优化的各分布式电源发电情况

4.3.1 基于出租车出行特征的充电行为下的能量管理优化结果

在建立的微电网最优经济运行模型的基础上，根据住宅用电量、光伏发电曲线，结合基于出租车出行特征的充电行为下场景一、二、三，对微电网内分布式电源未来24 h的发电情况进行优化。各场景下的最优发电计划如图11所示。

从图11可以看出，场景一下电动出租车只在夜晚充电，减小了白天微电网的负荷，光伏发电量基本满足负荷用电需求，GT只需进行小功率发电，ES在10：00~15：00期间进行持续性充电。在夜晚电动出租车入网充电，电网负荷量增加，GT与FC工作在高功率状态，ES也开始释放白天存储的能量，仅存在一次充放电。在场景二和三下，分别是电动出租车两次充电的时间段内和出租车空载率较高的时间段内GT与FC发电量较大，ES同样只进行一次充放电，情况与场景一类似。

4.3.2 基于微电网负荷稳定充电行为下的能量管理优化结果

在建立的微电网最优经济运行模型的基础上，根据住宅用电量、光伏发电曲线，结合基于微电网负荷稳定充电行为下的场景五，对微电网内分布式电源未来24 h的出力进行优化。其最优发电计划如图12所示。

图12 场景四下考虑经济性优化的各分布式电源发电情况

从图12可以看出，场景四下为保持微电网系统实时在线负荷量的稳定，让电动出租车充电负荷起到削峰填谷的作用，在这样的条件下各分布式电源发电也变得更加稳定，成本有所降低，更加符合期望。如前文所说场景四下用出租车进行调峰，但未考虑出行需求，可能会造成处于工作状态中的出租车不能满足人们出行需求的情况。

4.3.3 基于综合优化充电行为下的能量管理优化结果

在建立的微电网最优经济运行模型的基础上，根据预测的基于微电网负荷稳定充电行为，结合基于综合优化充电行为下的场景五，对微电网内分布式电源未来24 h的发电情况进行优化。其最优发电计划如图13所示。

图13 场景五下考虑经济性优化的各分布式电源发电情况

从图13可以看出，与场景四相比，场景五下各分布式电源发电不仅稳定性方面没有下降，且GT工作在较低功率状态下，成本也有所降低，同时考虑出租车空载率的问题，更加符合现实情况。

4.3.4 基于出租车无序充电行为下的能量管理优化结果

在建立的微电网最优经济运行模型的基础上，根据预测的家用负荷、光伏发电曲线，结合电动出租车无序充电的场景六，对微电网内各分布式电源未来24 h的发电情况进行优化求解。其最优发电计划如图14所示。

图14 场景六下考虑经济性优化的各分布式电源发电情况

从图14可以看出，场景六下由于电动出租车随机入网充电，各分布式电源发电情况受到家庭用电时间分布不均的影响，会有所波动。

经济性优化后不同场景下系统成本一并列于表2中。为更形象地对比，同时绘出对应的直方图，如图15所示。

图15 不同充电场景下的系统运营成本

4.4 结果对比分析

根据以上仿真结果，从微电网系统运行总成本和出租车空载率与在线的负荷峰谷差率几个方面进行对比。

由表2和图15可见，充电场景五在考虑与不考虑经济性优化的条件下都是最低的，且经济性优化后总费用降低了21.2%。在不考虑经济性优化时，综合考虑出租车出行特征与微电网负荷稳定性的充电场景五的总费用相较于场景六降低了18.1%。在考虑经济性优化时，综合考虑出租车出行特征与微电网负荷稳定性的充电场景五的总费用相较于成本最高的场景六降低了22.3%，即场景五在保证了空载率和负荷峰谷差率较优的前提下经济性也优于其他几种充电场景，更符合商业原则。

有序充电行为下的出租车负荷与住宅用电负荷的总负荷曲线如图16所示。表3列出不同充电场景下的出租车平均空载率和负荷峰谷差率的计算结果。

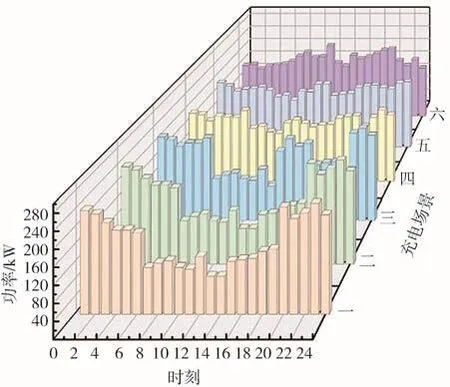
图16 出租车充电对微电网负荷的影响

由表3可见，场景一至场景三，峰谷差率都大于0.5，显然偏大；接着，场景五的空驶率和峰谷差率都比场景六小，说明场景五优于场景六；最后，对比场景五和场景四，后者虽然负荷峰谷差率很小，但空载率较大。因此，综合考虑出租车出行特征与微电网负荷稳定性，最终，平均空载率和负荷峰谷差率均小于0.3的场景五达到最好效果，有利于电网的安全运行。

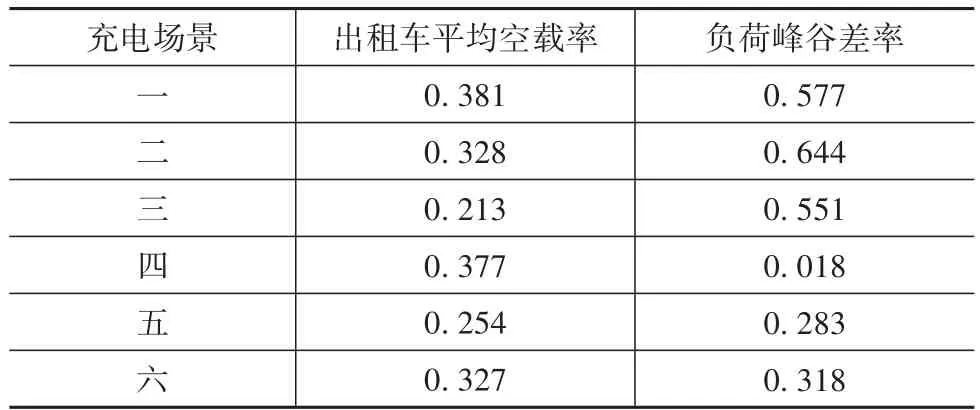
表3 不同充电场景下的出租车平均空载率和负荷峰谷差率

5 结论

以实测数据为基础，考虑出租车充电的不确定性，通过充电起始时间和持续时间，得到出租车充电负荷的时间分布，在此基础上制定了用户充电行为规则。以系统运行总成本为目标函数，并通过罚函数法构建适应度函数，建立计及出租车充电的微电网经济调度模型，对出租车不同充电场景进行经济性优化求解。结果表明，综合优化充电行为的空载率和负荷峰谷差率都在可接受范围内，且相比于未经经济性优化的充电行为其系统总成本可降低21.2%，更适合于实际应用。