多缸柴油机曲轴-轴承弹流润滑及动力学特性研究

于存银 国 杰 赵 建 张 恒 王仁智

（1.中国船舶及海洋工程设计研究院 上海 200011；2.哈尔滨工程大学 动力与能源工程学院 哈尔滨 150001）

0 引 言

内燃机的活塞-连杆-曲轴-轴承和各个部件连接处的油膜是一个复杂的系统，燃气压力和运动件的惯性力通过连杆作用在曲柄销上，最后力通过曲轴—轴承系统传递到整机。整个系统中，主轴承和曲轴之间通过油膜连接，油膜作为曲轴运动的动态边界条件，一方面避免其与主轴承直接产生干摩擦，另一方面油膜充当非线性的弹簧阻尼可以减小曲轴的振动。此外，曲轴的运动也会直接影响主轴承油膜的润滑参数，决定润滑质量。所以内燃机的曲轴-油膜-轴承系统是一个强耦合的系统，两者相互作用、相互影响。

在考虑油膜润滑求解轴心轨迹中，最早采用了3 种静力学方法：Hahn 方法、Holland 方法以及迁移率法，然而这3 种方法并未考虑轴颈的动力学效应。1982 年，陈伯贤和裘祖干将轴颈的惯性项计入轴心轨迹的动平衡方程中，进一步优化了动载滑动轴承轴心轨迹的算法。2003年，戴旭东等通过ADAMS 和自编Fortran 程序的联合分析了曲轴刚体动力学和主轴承润滑耦合的特性。之后，合肥工业大学桂长林等又在此基础上结合曲轴的柔性体动力学、曲轴轴颈倾斜等因素研究了曲轴的轴心轨迹和主轴承润滑特性，并采用柔度矩阵法进行了计入轴瓦弹性变形对轴承润滑的影响。方斌针对实船水润滑轴承总结出低黏弹流动压润滑刚度系数，并考虑了轴承支撑刚度的影响。2017年，大连海事大学的魏立队等利用商业软件建立了机体-曲轴的弹流润滑（Elastic Hydrodynamic Lubrication，EHD）耦合柔性体模型，结合有限体积法和有限元方法研究了船舶柴油机轴系振动特性。为了适应内燃机设计的快速化、简便化和低成本要求，实现建模方法的通用化和计算方法的模块化是进行内燃机高性能设计的必然要求。2000 年，MOURELATOS Z P采用子结构法对曲轴和机体进行有限元建模，然后利用NASTRAN 进行缩减模态自由度，并将提取的质量、刚度和阻尼矩阵数据输入到Fortran 里计算，大大减少了计算量并提高了计算速度。2003年，密西根大学的MA Zhengdong和PERKINS N C针对某整机的简化计算模型，提出一种快速计算多体动力学的方法，但计算局限于稳态条件下。2006 年，我国的雷宣扬等基于有限梁单元构造了整体曲轴模型，从而实现快速建模和仿真。

基于之前学者的理论和研究成果，为了实现建模计算的快速化和能够方便结构动力学的修改，本文提出了一种新的曲轴-轴承系统的建模计算方法，利用Fortran 语言编写计算程序。在之前学者采用基于静力变形的柔度矩阵法研究的弹流润滑基础上，借助于APDL 考虑了轴承组的瞬态动力学效应，使弹流润滑仿真计算更贴近实际物理工况，并且和不考虑轴承组变形的流体动力润滑（Hydrodynamic Lubrication，HD）计算结果进行了对比研究。

1 模型建立和理论基础

1.1 曲轴-轴承系统的激励源计算

图1 为4102 柴油机的活塞-连杆-曲轴模型。

图1 4102 柴油机活塞-连杆-曲轴模型

如该图所示，曲轴-轴承系统的主要激励源是作用于活塞上的燃气爆发压力和活塞-连杆等运动部件的惯性力，其动力学计算简化示意图如下页图2所示。

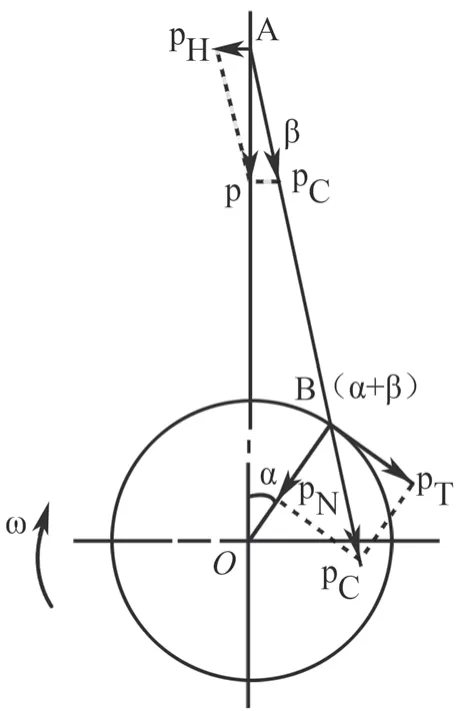
图2 简化示意图

曲柄销处作用力，连杆推力沿着连杆传递到曲柄销处，同时分解为曲柄销中心处的切向力和法向力，由此得到作用在曲轴上的的载荷。

1.2 曲轴的有限元模型

1.2.1 梁单元

如图3 所示，空间杆结构的梁单元，每个梁单元有2 个节点，每个节点拥有6 个自由度，即3 个平动自由度和3 个转动自由度。当杆受到外部载荷时，杆会发生3 个方向的位移变形以及3 个平面的弯曲转动变形。平动自由度的正方向是坐标轴正方向，转动自由度的正方向是以绕坐标轴方向右手螺旋定理确定的方向为正。

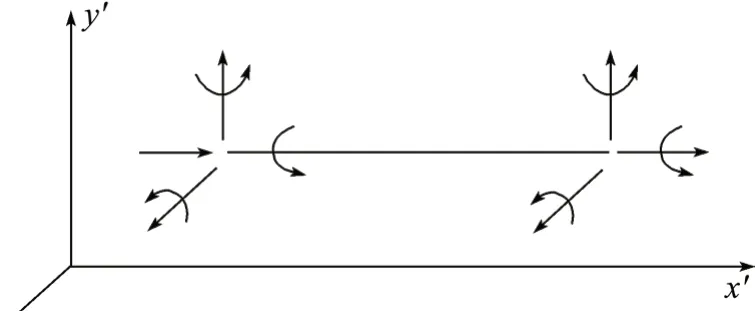
图3 空间杆结构的梁单元

1.2.2 曲轴有限元模型的构造

本文基于梁单元构造了曲轴的有限元模型。我们将曲轴分为4 个曲拐，因为4 个曲拐的结构以及材料参数相同，这样我们可以采用子结构法的思想，将曲轴分为4 个曲拐。只需要构造出其中1 个曲拐的有限元模型，便可计算整个曲轴的有限元模型，因此我们先构造出1 个曲拐的有限元模型。

我们将单个曲拐模型分为7 个梁单元，单个曲拐简化之后如图4 所示。

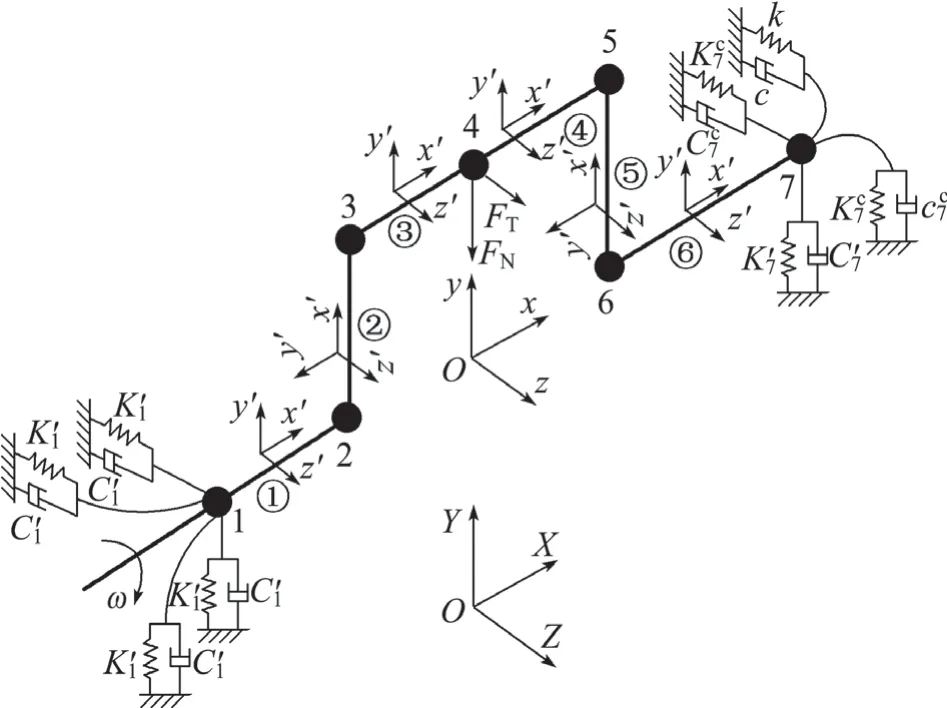
图4 单曲拐的有限梁单元模型

由于不同曲拐之间只是相位差不同，将1 个单曲拐模型简化成梁单元的超级单元之后，只需要整体调用梁单元集成的单曲拐有限元模型，从而实现整个曲轴有限梁单元的建立，其集成流程见图5。

图5 建模流程图

经过上述方法构造出如下页图6 所示的曲轴整体有限梁单元模型。该模型的位移边界条件是以油膜作支撑，载荷边界条件是作用于曲柄销上的激励源，整体支撑的机体认为是刚体。

图6 曲轴有限梁单元模型

1.3 轴承润滑理论

基于等温、不可压缩、等黏度的牛顿层流流体动载滑动轴承的Reynolds 方程为：

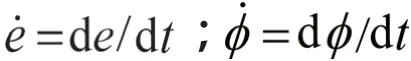
计入轴颈在轴承中发生倾斜时的油膜厚度方程：

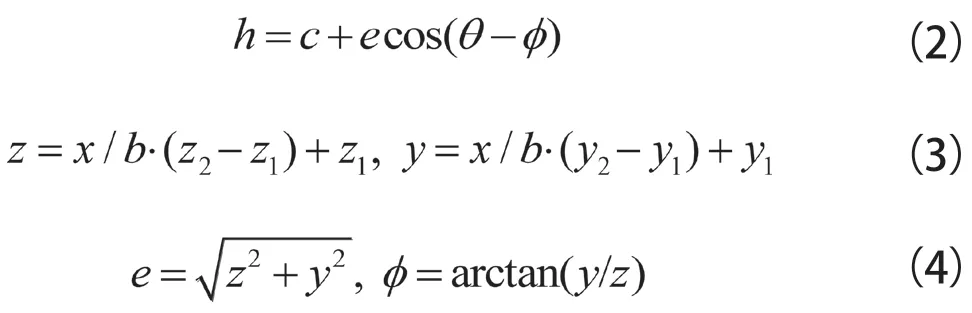
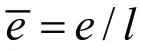
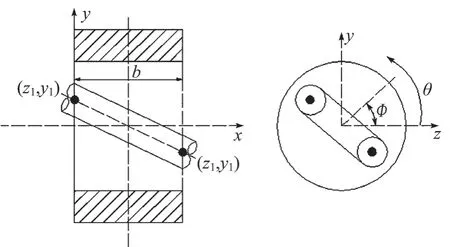
图7 轴颈倾斜的主轴承示意图

轴承油膜反力和反力矩为：

1.4 轴承座模型

轴承座的材料是灰铸铁（HT250），灰铸铁的弹性模量是157 GPa，泊松比是0.27，密度为 7 250 kg/m，采用的单元类型是Solid185，主轴承座的位移边界条件是在主轴承座的上部与机体连接的部分全部约束，认为刚度无限大，有限元模型和约束位置见图8。轴瓦表面的载荷边界条件是每一载荷步下的油膜力施加到相应的轴瓦表面节点上，轴瓦表面的网格节点和油膜的节点一一对应。

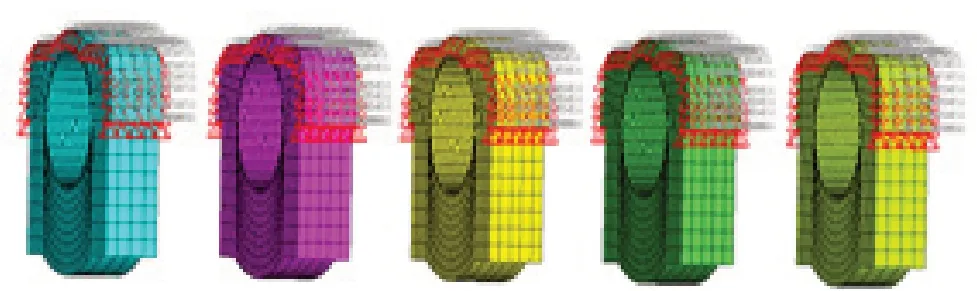
图8 轴承座有限元模型

2 数值计算方法

利用Fortran 语言自编的基于有限元方法计算曲轴动力学的程序和基于有限差分方法的求解轴承润滑的程序两者进行耦合计算，求解步骤如下，计算流程见图9。

图9 计算流程图

（1）设置主程序的计算仿真时间、计算步长、收敛精度和输出结果的控制。

（2）调用曲轴动力学的程序，输入曲轴的结构参数和尺寸，设置曲轴的初始条件，包括主轴颈的轴心的位置、速度以及主轴承处的轴颈的倾斜角。

（3）调用主轴承油膜润滑的程序，输入主轴承的结构参数和材料参数，设置计算的收敛精度。

（4）仿真开始，曲轴动力学输出主轴颈的轴心位移、速度和主轴颈在主轴承处发生的倾斜程度，通过瞬态动力学求解轴瓦表面的受载的变形量修正油膜厚度，油膜润滑程序得到曲轴的运行参数计算出主轴承的油膜压力，通过积分计算出作用在曲轴上的油膜反力和力矩。

（5）仿真时间达到，计算结果稳定，输出计算结果，否则重新设定仿真时间，重新计算。

3 模型计算和结果分析

以4102 柴油机为研究对象，验证上述计算方法。4102 柴油机的输入计算参数见下页表1，下页图10是气缸压力曲线，其计算的发火顺序是1-3-4-2。

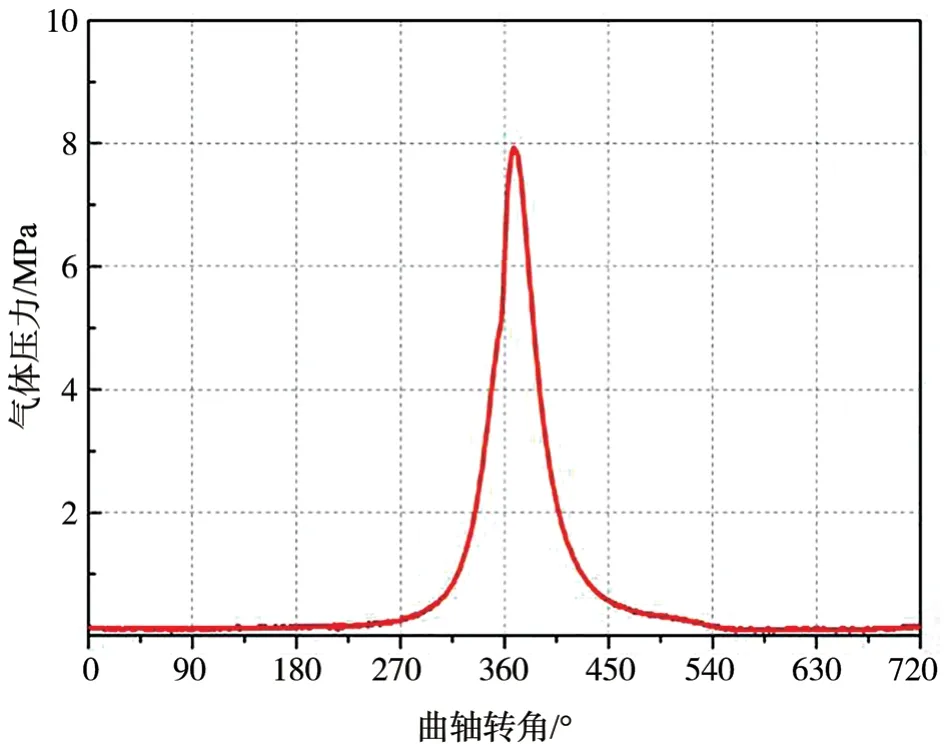
图10 气缸压力曲线

表1 柴油机计算参数

3.1 曲轴主轴承油膜反力

图11 和图12 分别是通过EHD 和HD 计算的各个主轴承的油膜反力，由图可见，总体趋势一致。第2、4 主轴承的油膜反力峰值最大，第1、5 轴承次之，中间第3 主轴承的油膜力峰值最小。EHD 计算的主轴承反力峰值依次是26 547 N、34 811 N、22 432 N、33 512 N、27 654 N，HD 计算的主轴承反力峰值依次是25 986 N、36 075 N、22 987 N、36 780 N、26 883 N。由此可见：考虑轴承的瞬态弹性变形，整体的轴承反力是降低的，但是曲轴两端主轴承的油膜反力整体提高了，这体现了曲轴动力学和轴承座动力学之间的耦合关系。

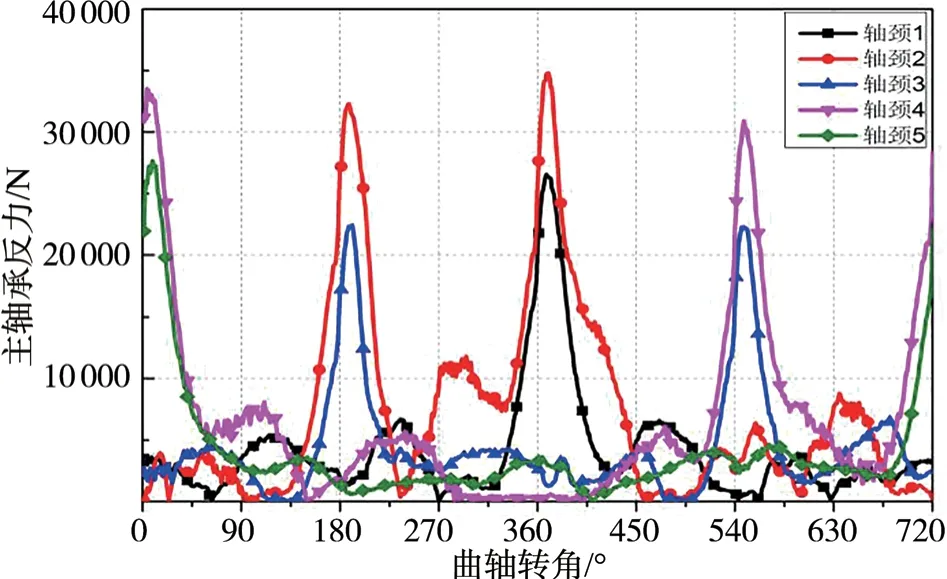
图11 弹流润滑的主轴承油膜反力

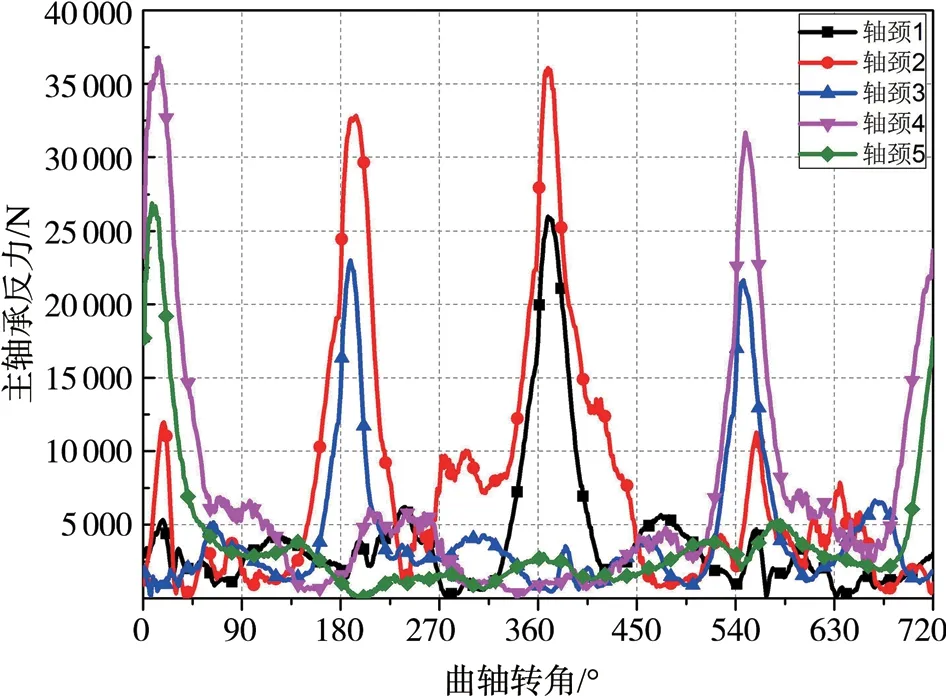
图12 流体动力润滑的主轴承油膜反力

3.2 曲轴主轴颈动力学特性

图13 和图14 所示分别是EHD 和HD 计算的主轴颈的受载倾斜程度，比较计算结果见表2。主轴颈在主轴承处由于受载变形产生的倾斜，从图中可以发现主轴颈1、5 的倾斜程度最严重。

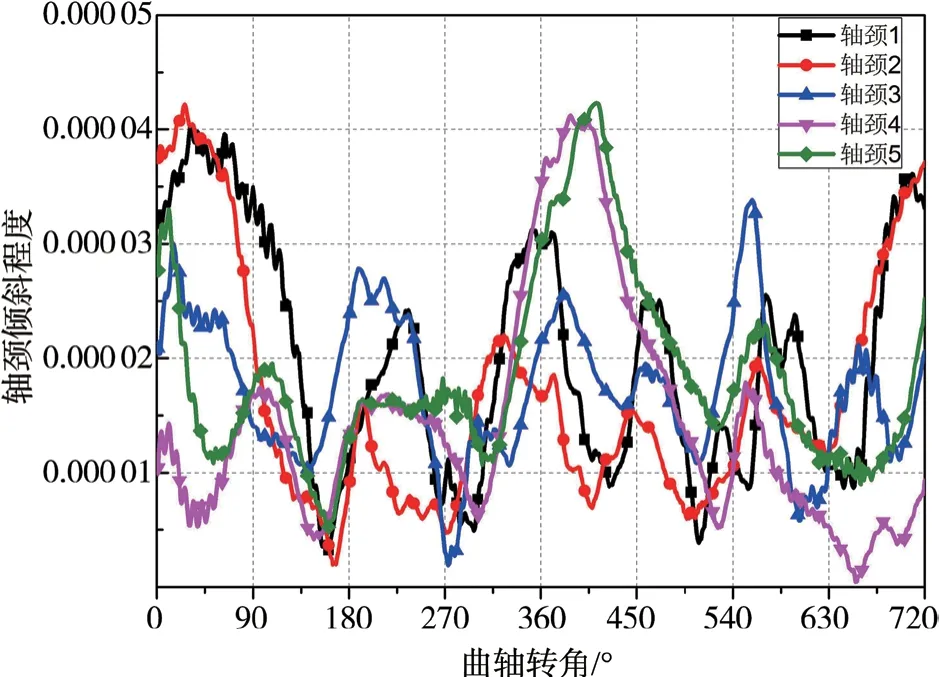
图13 弹流润滑的主轴颈的倾斜程度

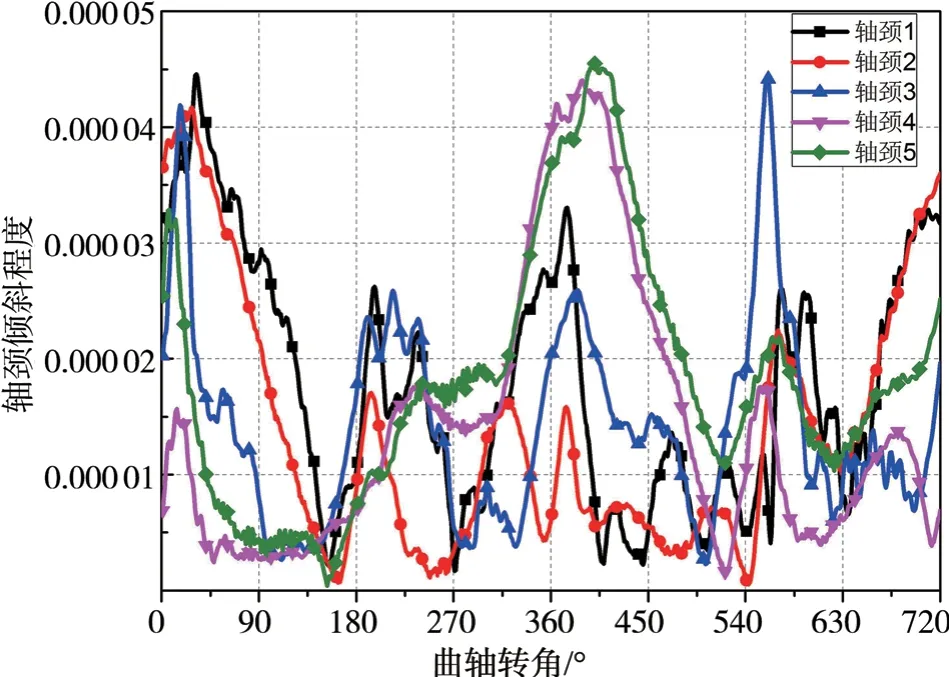
图14 流体动力润滑的主轴颈的倾斜程度

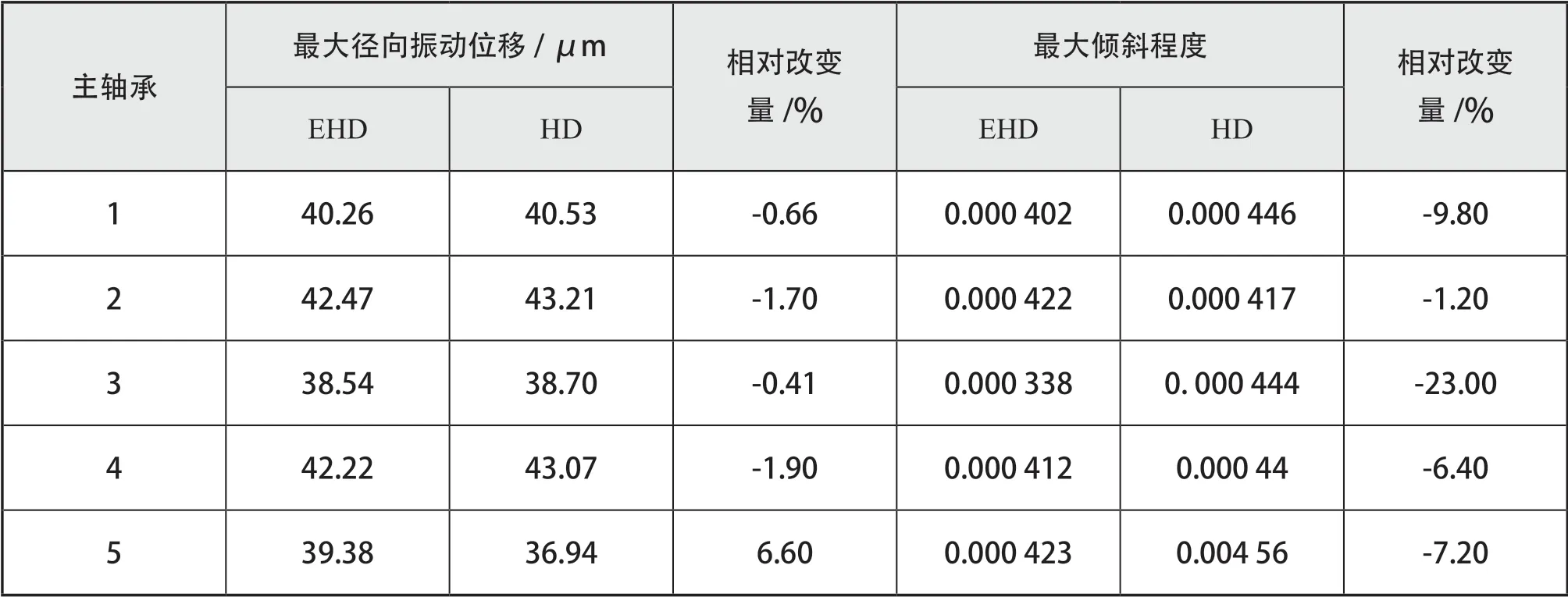
表2 5 个主轴颈的动力学特性比较

这种情况主要是因为主轴颈1、5 处于曲轴两端，只有一侧因受外部载荷而弯曲变形，从而导致倾斜严重；而主轴颈2、3、4 两边同时受载，所以在一定程度上可实现两侧力和力矩的平衡抵消，尤其是主轴颈3 的倾斜程度最小。在EHD计算下，因油膜压力的偏置使轴承发生弹性变形、油膜厚度增加，油膜压力分布趋于减小，使得作用于主轴颈的倾斜力矩减小，所以整体倾斜程度减小。

以EHD 和HD 计算的曲轴径向振动位移与比较计算结果见图15、图16 和表2。由于在外载荷的作用下，曲轴轴颈的运动规律是周期性的，曲轴的外载荷主要源于燃气压力和往复惯性力以及离心惯性力，但是振动规律主要还是取决于气缸压力和往复惯性力的强迫作用。由于主轴颈1 的相邻气缸是气缸1，故其运动规律主要受到气缸1的载荷影响，四缸机的发火顺序是1-3-4-2，所以主轴颈1 在气缸1 发火时的径向振动最剧烈，受到其他气缸的发火作用的效果由近及远；主轴颈2 同时受到气缸1 和气缸2 的作用，所以其径向振动的峰值主要在180°和360°附近；受到柴油机对称结构的影响，主轴颈3 位于中间位置，所以其同时受到相邻气缸2 和气缸3 的影响，180°和540°附近的径向振动最剧烈，其次受到较远气缸的影响，所以其振动规律具有极强的对称性和周期性；因为主轴颈5、4 是和主轴颈1、2 以主轴颈3 为对称，所以其振动规律是相似的，只是受到发火顺序的影响，存在相位差，但幅值和趋势是一致的，总体上的峰值和趋势变化一致。

图15 弹流润滑的曲轴径向振动位移

图16 流体动力润滑的曲轴径向振动位移

EHD 计算的主轴颈径向振动位移整体偏小，主要原因是轴承的瞬态弹性变形吸收了一部分能量，导致主轴承润滑参数发生改变。主轴颈5 的振动位移变化和其他主轴颈的振动位移变化趋势不一致，主要原因在于主轴颈5 发生了严重倾斜。

3.3 主轴承润滑特性

下页图17 至图20 所示分别是以EHD 和HD计算的主轴承的最小油膜厚度以及最大油膜压力，具体计算结果差异比较参见表3。主轴承的最小油膜厚度和最大油膜压力在一个工作循环内的变化规律基本是负相关的。最小油膜厚度越小，其最大油膜压力越大，变化规律基本符合油膜润滑的动压效应，但是由于油膜压力同时受到轴颈的挤压效应影响，所以从图中也可以发现，即使油膜厚度相同，但是最大油膜压力却相差很大，这说明油膜挤压效应在流体润滑计算中是不可忽略的。EHD 的计算结果显示主轴承的最大油膜压力都降低了，尤其是主轴承2 和 4 变化最明显。主轴承2 的最大油膜压力降低最大，但是最小油膜厚度并没有增加。通过前页的表2 也可判断，有可能是轴颈2 发生严重倾斜，由此也证明了考虑轴颈倾斜的必要性。

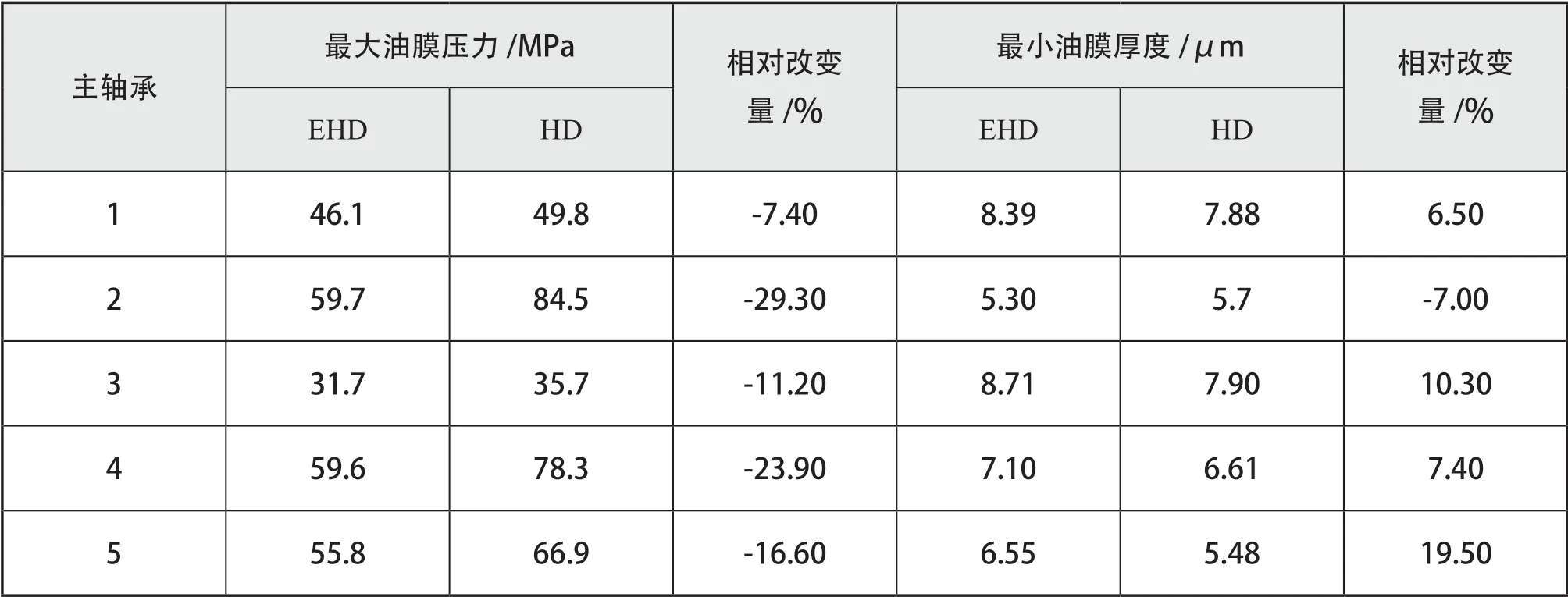
表3 5个主轴承的润滑特性比较

图17 弹流润滑的主轴承最小油膜厚度

图20 流体动力润滑的主轴承最大油膜压力

图18 流体动力润滑的主轴承最小油膜厚度

图19 弹流润滑的主轴承最大油膜压力

4 结 论

（1）通过有限元和有限差分的方法实现了活塞-连杆-曲轴-油膜-轴承系统的建模，实现了参数化和模块化，能够进行系统的快速数值仿真，具有通用性，便于结构动力学修改。

（2）整体曲轴-轴承系统的动力学特性和润滑特性的变化都呈现对称性和周期性的规律，这种现象和柴油机的结构相符合。

（3）将弹流润滑和流体动力润滑的计算结果进行了对比，发现考虑轴承的瞬态动力学计算的轴承变形对曲轴动力学以及轴承润滑特性影响很大，主轴颈的径向振动位移和倾斜程度都有减小趋势，尤其第3 主轴承的轴颈倾斜程度减小23%；所有主轴承的最大油膜压力都减小，尤其第2 和第4 主轴承的最大油膜压力分别减小29.3%和23.9%。

（4）目前只是研究了考虑轴颈倾斜影响的曲轴动力学和轴承润滑特性，而没有考虑到在油膜载荷下的轴承座动力学特性，下一步将对轴承座的动变形进行评价。