混合方幂的华林-哥德巴赫问题的例外集
2022-05-02朱豆豆
朱豆豆
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
0 引言
混合幂Waring-Goldbach问题主要研究将正整数n表示为
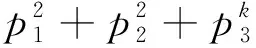
其中,
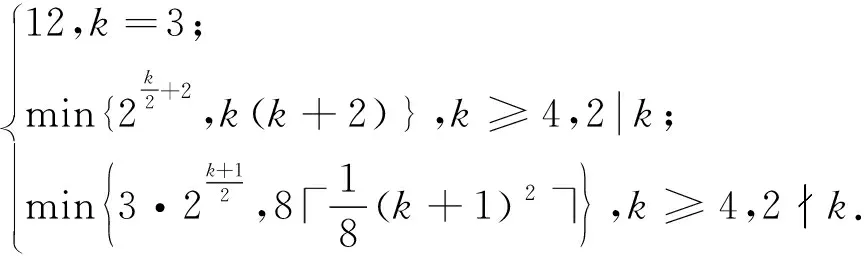
θ(k)=
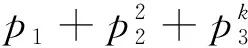
2012年,李太玉[5]将例外集的上界改进为
2018年,刘志新等[3]将结果改进为
此外,Kumchev等[6-11]在这类问题的研究中取得了重要结果.同时,一些新的方法也发展起来,为此类问题的研究提供了一般方法.本文主要应用圆法并结合文献[12]的思想得出结果.
1 预备知识
首先介绍一下本文用到的一些记号和术语.


为了清晰地说明定理1的证明思路,下面给出一些必要定义.
对于k=1,3,5,7,定义
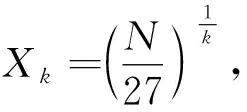
设
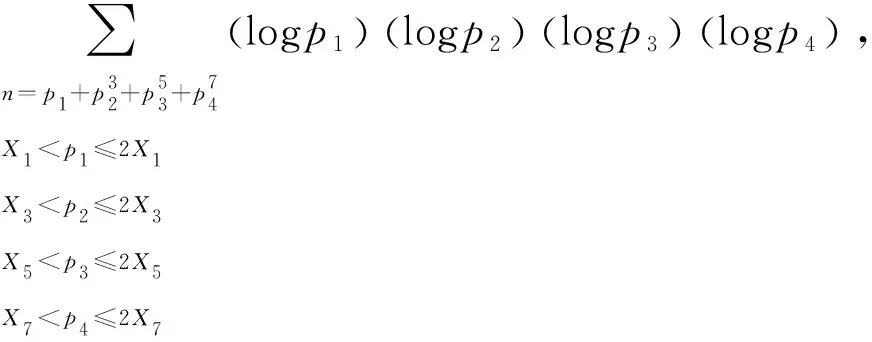
则对任意Q>0,有
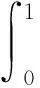
取
(1)
定义主区间M和余区间m如下:
(2)
其中,
则
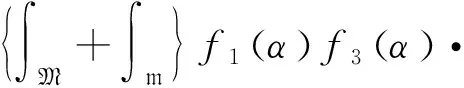
进一步,设
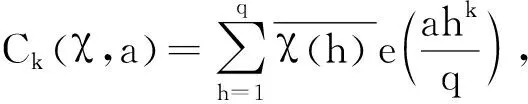
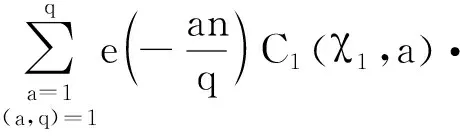
记

(3)
则有命题1成立:
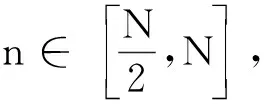
其中S(n)是由(3)定义的奇异级数.该奇异级数绝对收敛且对于任意的偶数n和某个固定常数c*,有
0 (4) I(n)定义为 命题1的证明将在第三节给出,对奇异级数性质的讨论将在第四节给出.定理的证明还需要如下引理: 首先定义可乘函数ωk(q)如下: 对于整数k≥3和集合A⊆(U,2U]∩N,定义 (5) 引理1[12]对于γ∈R以及X≤U,定义 则L(γ)≪X2U-k(logU)Ak,其中ck和Ak是依赖于k∈N的常数. 引理2[12]对于1≤a≤q≤Uk21-k以及(a,q)=1,定义 M(q,a)={α:|qα-a|≤Uk(21-k-1)}, 设M是区间m(q,a)的并,取 假设G(α)和h(α)是周期为1的可积函数,g(α)=gA(α)如(5)定义,m⊆[0,1)是一个可测集,则 引理3若P,Q满足(1),余区间m如(2)定义所示,则 这里α满足条件: 因为对于Q*的选取满足Q* 这两种情况均有q(1+N|λ|)≫P,所以 最后的≪只依赖于(1)中的P的选取. 由命题1, 记 根据引理3,对应的 则 由于 其中M如引理2中定义所示,则应用引理1可得 J0≪Lc. 则 因此 在证明命题1之前,首先引入一些符号.当k=1,3,5,7时,对于Dirichlet特征χmodq,定义 其中δχ=1或者0取决于Dirichlet特征χ是否为主特征. 现在引入Dirichlet特征,对于(a,q)=1,根据Dirichlet特征的正交性,容易得到 定义集合Lj(j=1,2,…,16)如下: 若j=1,2,…,16,则Lj分别为{1,3,5,7}、{1,3,5}、{1,3,7}、{1,5,7}、{3,5,7}、{1,3}、{1,5}、{1,7}、{3,5}、{3,7}、{5,7}、{1}、{3}、{5}、{7}、{∅}. (6) 其中 这里I1可以用常规方法估计,需用到如下引理: 引理4[14]当(a,q)=1时,对于Dirichlet特征χmodq,有 引理5对于k=1,3,5,7,设χkmodrk是原特征,χ0modq是主特征,r0=[r1,r3,r5,r7],则 (7) 证明通过引理4可得 则式(7)左侧 接下来估计I1.对于k=1,3,5,7,根据文献[15]引理可得, (8) 将(8)代入I1得 (9) 由估计 (10) 并且令r0=1,由引理5,(9)中的余项 因此,式(9)可表示为 (11) 为了证明命题1,仅需证明对于j=2,…,16, 下面用文献[16]中的迭代方法估计I2,…,I16的贡献.为此,对于k=1,3,5,7,设 关于Jk(g)和Kk(g)的估计,有如下结论: 引理8当P,Q满足条件(1)时,有J1(1)≪NL-A. 引理 6~8的证明与文献[17]中的引理的证明类似,在此略去. 首先从I16开始估计,这是最复杂的一项. 其中,χ0modq是主特征,r0=[r1,r3,r5,r7]. 对于k=1,3,5,7,当q≤P,Xk 在最后一个积分中运用柯西不等式,则 因为r0=[r1,r3,r5,r7]=[[r1,r3,r5],r7],[r1,r3,r5]=[[r1,r3],r5],应用引理6、引理7及引理8可得 (12) 在对I2,…,I15估计时,需结合由(8),(10)得出的以下估计: 利用处理I16类似的方法可得: (13) 结合(6)(11)(12)(13),命题1得证. 首先给出本节所需引理.对于k≥1,定义 引理9[18]若(p,a)=1,则 引理10对于(p,n)=1,有 (14) 证明记式(14)左侧为S,通过引理9,有 若k∈{3,5,7},有|Ak|=0,则S=0.否则, 由引理9知三重的外部和不超过 ((3,p-1)-1)((5,p-1)-1) 因为对于主特征χ0modp,T(χ0)=-1,所以 引理11设L(p,n)为下列同余方程的解的个数: 则对于任意的正偶数n,有L(p,n)>0. 证明 其中 由引理9, 所以当p≥18时,|Ep|<(p-1)4,因此L(p,n)>0.当p<18时,可以直接核对,知L(p,n)>0. 引理12A(n,q)是关于q的可乘函数. 证明由(3)知,只需证明B(n,q)是关于q的可乘函数.设q=q1q2,(q1,q2)=1,则 (15) 因为(q1,q2)=1,则 (16) 把(16)代入(15),得 引理13设A(n,q)如(3)所示,则 (2)存在一个绝对正的常数c*>0,对于任意的正偶数n,有 S(n)≥c*>0. 证明由引理12知B(n,q)是关于q的可乘函数,因此,有 (17) (18) 记R(p,a):=C3(p,a)C5(p,a)C7(p,a)-S3(p,a)S5(p,a)S7(p,a),则 (19) |A(n,p)|≤|μ(p)·c2p-2|≤c2p-2. (20) 另外,若直接运用引理4,则 因此 (21) 令c3=max(c2,6720),则对于无平方因子的q, 因此,由式(18)可得 则引理13中(1)式成立.又由引理12可得, (22) 由式(20), (23) 又由式(21)知 (24) 另外,由引理11知,当n为正偶数时,对于任意的p有L(p,n)>0.因此 所以 (25) 结合(22)~(25),令c*=c4c5c6>0,则 S(n)≥c*>0. 由引理13即得奇异级数S(n)绝对收敛且有式(4)成立,结合第三节论述可知在主区间上有命题1成立.由命题1及第一节相关论述可得结论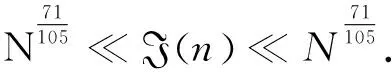


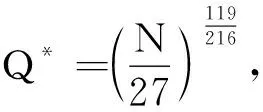
2 定理1的证明



3 命题1的证明

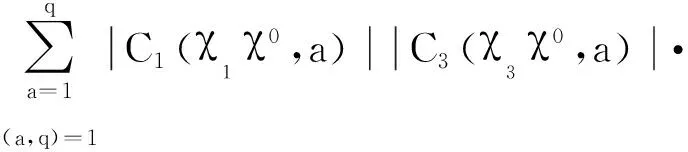
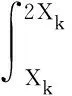
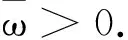

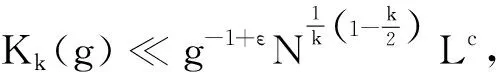
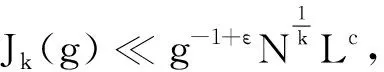
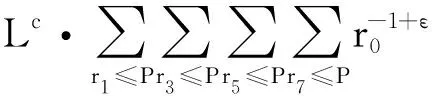
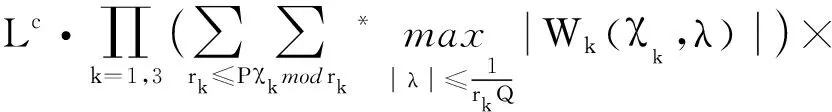
4 奇异级数
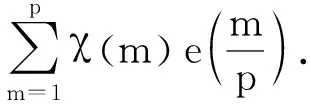
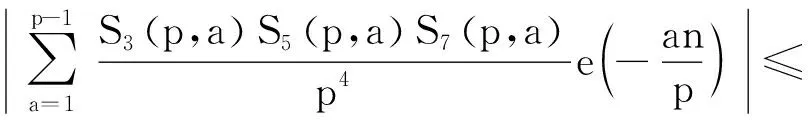
((7,p-1)-1)≤48项.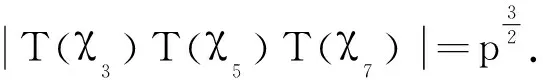

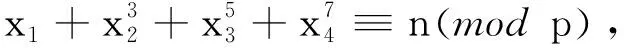

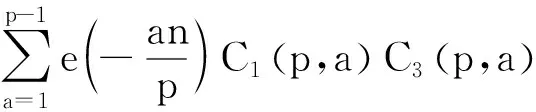
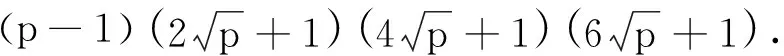
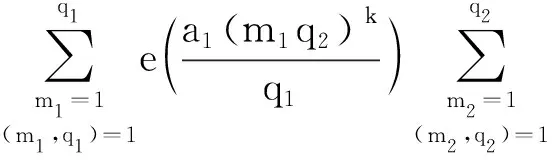
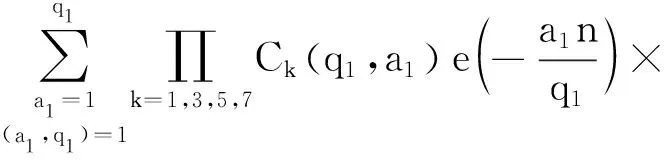

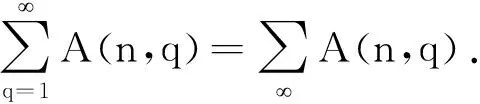
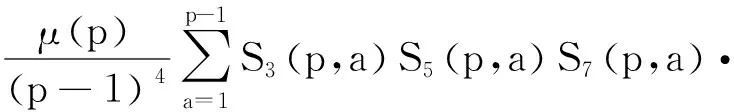
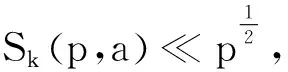
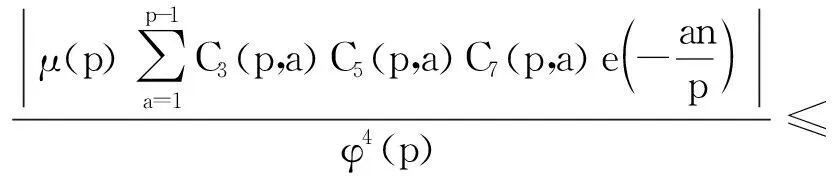


5 结语
