基于轮廓恢复和最小二乘修正的三维Mesh优化
2022-04-29尹旷王红斌方健胡帆覃煜张奇源
尹旷 王红斌 方健 胡帆 覃煜 张奇源
摘要:在由密集点云生成的初始Mesh网中存在较多冗余数据、噪声和细节损失,具体表现为:初始Mesh网往往存在非流行、棱角钝化和平面凹凸等问题,上述问题会严重影响三维重建的精度和效果。传统的先简化再优化的Mesh处理策略尽管可以减少冗余数据、提升Mesh的平滑性,但容易使Mesh丢失细节信息。为解决上述问题,提出采用简化—优化结合并迭代执行的策略,通过简化恢复模型轮廓和棱角,并采用最小二乘法精确求解Mesh中三角网顶点的改正量,进而实现对Mesh的精细优化。
关键词:Mesh优化;最小二乘;轮廓恢复;三维重建
中图分类号:TP39文献标志码:A文章编号:1008-1739(2022)17-67-05

0引言
近年来,智慧城市的建设在国内外不断推进。在智慧城市建设中,一个核心的问题是高效、低成本、快速地获取城市场景的三维模型,而传统手工建模方式由于其低效、高成本、低现势性已不能满足要求。随着无人机倾斜摄影测量三维重建技术的不断成熟,将有效解决城市三维重建中存在的上述问题。无人机具有灵活性高、成本低、飞行条件要求低、可快速获取数据等特点,在大比例尺测图、实时响应、应急救援以及三维重建中具有独特的优势和应用前景[1]。利用无人机搭载多台相机从一个或多个不同角度对同一物体或场景倾斜摄影,用无人机影像进行真实三维表面模型的重建是计算机视觉和摄影测量领域的重要研究内容[2-5]。
基于影像的三维重建可以描述为根据已知的摄影中心和方向、光照等条件,由物体或场景的一系列影像,对其表面进行三维形状的最佳估计问题[6]。基于影像三维重建的主要流程为:自动空中三角测量、影像密集匹配、构网和纹理贴图[3]。基于影像的三维重建技术能够得到现势性强、可视化效果好的三维实景模型,但是该技术在具体应用中仍存在着一些问题。例如在密集匹配方面,目前还没有一种精度和效率都很优秀的匹配算法能完全满足城市场景三维重建对密集匹配精度和效率的要求。如SGM[7]和COLMAP开源库中的PatchMatch[8]算法尽管可以生成效果较好的密集点云,但匹配效率较低。因此,密集匹配一直是计算机视觉领域的研究热点。另外,由密集点云构三维Mesh网更加关注三角网的点面关系、可视性等信息,往往会损失较多细节,导致三维模型的细节表达性能较弱。
由于密集匹配和构网后Mesh网中存在较多噪声和细节损失,初始网往往存在非流行、孔洞及棱角钝化、平面凹凸等问题,会严重影响三维重建的效果。降低冗余数据量,提升重建模型的细节信息是实景三维重建研究领域亟待解决的问题。通过对原始Mesh网做简化—优化相结合的迭代处理是解決上述问题的一种有效的手段。Mesh简化可以降低Mesh的冗余数据量,增强Mesh的各向异性。Mesh优化可以去除Mesh中的噪声,并提升Mesh对模型细节的表达性能。在Mesh优化方面,当前的主流是采用影像匹配方法对最佳表面位置进行估计[9-11],实现对三维模型的网形和准确度的优化。该方法可以提升模型细节和平滑度,但也存在一些问题:如表面优化过程的效率较低,模型棱角和轮廓钝化严重等。为此,本文提出采用简化-优化相结合的策略,通过简化恢复模型轮廓和棱角,并采用最小二乘法精确求解Mesh中三角形的顶点移动量,进而实现对Mesh的精细优化。
1三维轮廓恢复
三维表面轮廓指场景中物体的边缘轮廓线或较大平面区域,如房屋的棱角、台阶的棱沿以及平面墙壁等。三维轮廓的恢复对提升三维模型的细节层次及视觉效果起着至关重要的作用。为了提升Mesh的重建效果,Mesh处理的目标是得到各向异性较强的Mesh网。具体地,对于平面区域会利用大三角面去表达,对于边缘和棱角区域,一般采用狭长和较为密集的三角面去表达。传统方法一般采用先简化后优化的策略,Mesh简化可以减低网格的冗余度和去除非流行,但简化比的参数较难准确给定,所以Mesh简化往往会造成网格细节信息损失的问题。Mesh优化的目的是提升网格对物体表达的精度,需要网格具备足够的细节信息。
目前,比较有代表性的方法是文献[12]中提出的优化方法,该方法通过采用多层级金字塔的方法对三维模型由粗到精的优化。在金字塔的最底层是在原始影像1/4尺度下对初始网进行简化,通过简化过滤初始网中代价低的三角形,降低细小三角形和原始网中的噪声顶点对后续优化的影响。随着金字塔层级的升高,三角网得到进一步细分,网的表面细节得到进一步优化。上述方法中存在三角面过度细分的问题,会影响轮廓构建。为解决上述问题,本文采用一种简化—优化结合的迭代优化策略:简化操作可修正三角面的法向量,构造大平面和棱角处轮廓,为网形优化提供更准确的轮廓位置和法向量初始值;优化操作可提升网的细节信息。本文方法中一次简化和金字塔各层级的优化为一次迭代,根据初始网平滑度和每一次迭代处理的优化目标,选取不同的简化比和梯度下降优化次数,从而实现整体轮廓的恢复和和表面细节的积累。
本文方法流程如图1所示。
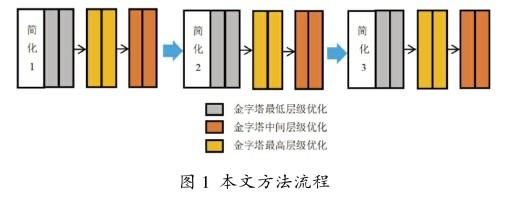
简化—优化恢复轮廓效果如图2所示。简化—优化最终结果如图3所示。

2基于最小二乘解算的Mesh顶点移动量分配
通过影像匹配可获得同一物点在多幅影像上对应的像素点和该物点的优化移动量。在由密集点云构建Mesh后,不属于三角形的冗余物点将会分布在Mesh中三角形的内部。一般,密集点云中的大部分点在构建Mesh后是冗余点,分布在Mesh中的三角网内。三角网的位置优化是通过移动三角网中所有三角形顶点实现。为了更精确地计算三角形顶点的移动量,可将每个三角形内所有物点(内点,下同)的移动量分配到三角形的顶点上。内点移动量的分配,实质是三角面内的表面优化能量离散化到三角形顶点上的问题。
物点改正量计算如图4所示。



上述是三角形在一个立体像对中顶点坐标改正优化的过程,考虑到Mesh中每个三角形都可被多个立体像对可见。所以在具体优化时,Mesh中三角形的顶点改正量是根据可视性强弱对每个立体像对求得改正量并做加权平均。
3实验与分析
为了验证本文方法对Mesh优化的有效性,对近景拍摄的影像做空三、密集匹配和构网处理后得到初始Mesh网,数据信息如表1所示。然后,分别采用文献[13]中的方法(借助OpenMVS开源库的实现)和本文方法对初始Mesh网做优化处理。
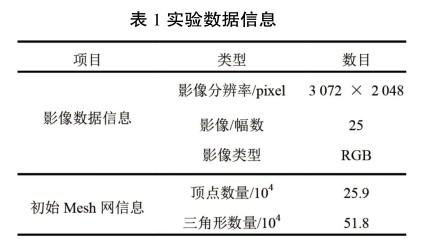
3.1实验结果
初始Mesh网如图6所示。
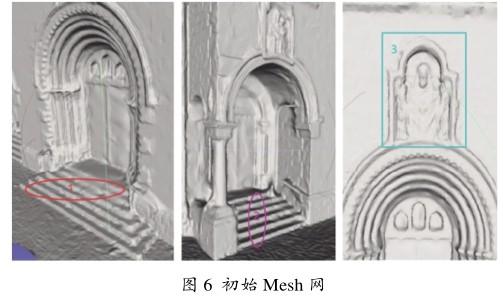
在Vu和本文方法分别对初始Mesh网优化后,在细节层次上对优化效果做了对比。Vu方法优化后的结果如图7(a)所示,本文方法优化的结果如图7(b)所示。在Vu方法优化后,Mesh网中的顶点个数为287 000,三角面个数为575 000。本文方法优化后Mesh网中的顶点个数为166 000,三角面个数为332 000。

3.2實验分析
首先,对Mesh网轮廓恢复的效果进行分析。从图3可以看出,在采用本文方法对Mesh优化时,随着简化—优化迭代的进行,细小三角面被不断地剔除,三角面的法线方向得到修正,轮廓被逐渐恢复。在优化后平面区域更为平坦,棱角处更为锐利。从图4可以看出,本文方法对平面和棱角区域的优化效果更好。
在轮廓恢复的基础上加入最小二乘法去精确求解Mesh中三角形顶点的改正量,从而实现Mesh优化,优化效果如图7(b)所示。对比图7(a)和图7(b)可以发现,在棱角处(1号和2号椭圆区域),由于本文方法采用简化降低冗余数据并修正了三角面的法向量,故本文方法优化后棱角更为锐利。本文方法冗余数据量低,法向量准确对Mesh优化的贡献也体现在平面区域(3号方框内)。所以,相较于Vu方法,采用本文简化—优化组合处理的方法,在对Mesh优化后可提升Mesh网的细节,并增强Mesh网的各向异性。
4结束语
针对采用影像匹配最佳表面估计法对三维Mesh优化时存在棱角钝化、像素力量到顶点分配不准确导致优化后的Mesh细节层次信息损失严重的问题,本文提出采用轮廓恢复和基于最小二乘法修正三角网的顶点移动量对初始Mesh进行优化。在采用本文方法对Mesh做优化后与Vu方法做对比,验证了本文方法对Mesh网优化具有更好的效果。
参考文献
[1]傅桂霞.基于AUV测量信息的时空3D数据地形构建[D].哈尔滨:哈尔滨工程大学, 2011.
[2]王辰.基于影像的三角网表面模型优化[D].武汉:武汉大学, 2019.
[3]刘健辰.基于倾斜影像的Mesh模型自动构建方法研究[D].武汉:武汉大学, 2017.
[4张春森,张梦辉,郭丙轩,等.影像三维重建的网格自适应快速优化[J].武汉大学学报(信息科学版),2020,45(3):411-418.
[5] DUAN Y , YANG L , QIN H , et al. Shape Reconstruction from 3D and 2D Data Using PDE-Based Deformable Surfaces[C]// European Conference on Computer Vision. Springer. Berlin: Springer,2004:238-251.
[6] SORKINE O,COHEN-OR D.Least-squares Meshes[C]// Proceedings Shape Modeling Application. Genova:IEEE, 2004:191-199.
[7] HIRSCHMULLER H. Stereo Processing by Semi-Global Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328-341.
[8] DRORY A,HAUBOLD C,AVIDAN S,et al.Semi-global Matching:A Principled Derivation in Terms of Message Passing[C]//Lecture Notes in Computer Science.Berlin: Springer,2014:43-53.
[9] ZHENG E L, DUNN E,JOJIC V,et al. PatchMatch Based Joint View Selection and Depthmap Estimation[C]//IEEE Conference on Computer Vision and Pattern Recognition. Columbus:IEEE,2014:1510-1517.
[10] NEALEN A,SORKINE O,ALEXA M,et al. A Sketch-based Interface for Detail-preserving Mesh Editing[J].ACM Transactions on Graphics (TOG),2005,24(3):1142-1147.
[11] NEALEN A, IGARASHI T, SORKINE O,et al. Laplacian Mesh Optimization[C]//Proceedings of the 4th International Conference on Computer Graphics and Interactive Techniques in Australasia and Southeast Asia.Kuala Lumpur:ACM,2006:381-389.
[12] VU H H, LABATUT P,PONS J P,et al.High Accuracy and Visibility Consistent Dense Multiview Stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012:34(5):889-901.
