基于Grover 算法的布尔二次方程组求解

钱宇梁 舒国强 封聪聪 邸诗秦

摘要：布尔方程组求解问题在密码等领域有着广泛而重要的研究意义，其中主要是非线性的布尔方程组求解较为困难。已知的经典求解算法的复杂度高，求解效率低下，而目前量子算法的加速优势为量子计算求解布尔方程组带来的新的可能，文章旨在应用已知的Grover算法进行求解，可为求解带来开平方的加速优势。同时，为了在量子计算机有限的资源上发挥最大求解能力，文章提出比特资源优化和线路深度优化的方案，通过实验证明了该方案的有效性，大大提高了当前设备的求解能力。

关键词：布尔二次方程;Grover 算法;二次加速;量子计算;线路优化

中图法分类号：0413文献标识码：A

Solving Boolean quadratic equations based on grover algorithm

QIAN Yuliang'，SHUGuoqiang，FENG Congcong2，DI Shiqin

（1.XuteliSchool，Beijing Institute of Technology，Beijing 102488，China;

2.State Key Laboratory of Mathematical Engineering and Advanced Computing，Zhengzhou 450000，China）

Abstract：The problem of solving Boolean equations has extensive and important research significance in cryptography and other fields， and it is mainly difficult to solve nonlinear Boolean equations. The known classical solution algorithms have high complexity and low efficiency. The current acceleration advantage of quantum algorithms brings new possibilities for quantum computing to solve Boolean equations. This paper aims to use the known Grover algorithm， which can bring quadratic acceleration advantages. At the same time， for maximizing the computing ability on the limited resources of the quantum computers， we propose a scheme of bit resource optimization and circuit depth optimization. The effectiveness of the scheme is demonstrated by experiments， which greatly improves the computing ability of the current equipments.

Key words： Boolean quadratic equations， Grover algorithm， quadratic acceleration，quantumcomputing，circuit optimization

1相關工作

一直以来，布尔方程组求解问题都是密码学等领域的重要研究问题。序列密码、分组密码和 Hash 函数的设计与分析是目前信息安全领域的前沿、热点问题。布尔函数作为序列密码、分组密码和 Hash 函数中的重要组件，其密码学性质的好坏直接关系到密码体制的安全性。近年来，代数攻击引起了国内外的密码学者的注意，代数攻击的基本思想就是：一个密码算法可以表示为一个大的多变元多项式方程组，求解这个方程组就可以得到密钥，并且这些方程组以非线性居多。

当前，求解多元非线性的布尔方程组的方法通常有grobner基方法，其求解的复杂度的上限是 O（2n ）[1]。暴力搜索法的复杂度是 O（ n2n ）[2]。XL 方法的复杂度是nO（1/ε）[3～4]等。其他的求解思路是通过增加变元的方式将非线性方程组转化为线性方程组，再利用线性方程组的求解方法求解，常见的如 Gauss 消元法，复杂度是 O（ n3）[5];回溯法，复杂度是 O（ n！）等方法进行求解。然而，这些算法的求解效率并不高。量子计算是以量子物理学为基本原理，通过对多个量子叠加态并行处理，实现对经典算法速度的二次加速甚至指数级加速。近年来，量子算法已经展示了量子计算的巨大潜力。其中，HHl算法在求解高维稀疏方程组问题上展现了指数级的加速，且广泛应用于机器学习等领域。GAO 等[6]将改进HHl算法应用到布尔方程组的求解问题上，展示了指数级的加速。但是，该算法目前面临很多实际的应用困难，比如初态的制备问题还无法取得突破。

在无序数据库搜索问题上，Grover 算法能够以开平方级的加速实现求解。且对其的研究也有了一定的成果[7～9]。Grover 算法在实际问题的应用方面，相关学者已经做出了大量有关的研究。早在2000年时，ZALKA 等[10]就已经提出使用 Grover 搜索算法进行数据库搜索。2006年，YAMASHITA[11]提出了如何在通用编程中使用 Grover 搜索算法加速程序。近年来，国内学者也开始重视 Grover 搜索算法的应用，如在2014年，阮越等[12]提出了基于 Grover 搜索算法的人脸识别算法，将人脸识别的效率在经典基础上进行了二次加速;同年，PENG 等[13]提出了基于 Grover 搜索算法的无线量子网络路由算法，可以在限定跳数内搜索出目标路径。2015年，SUN 等[14]提出了基于 Grover 搜索算法的量子求根算法，将算法复杂度降低到了 O    。从大量的文献中可以看出，Grover 搜索算法的应用范围较广，具有很高的研究价值。

本文的主要工作是研究应用 Grover 算法求解二次非线性布尔方程组。已知布尔方程组求解具有广泛的应用，且目前经典算法求解效率不高。针对 n 元2次布尔方程组，本文基于量子 Grover 算法实现对方程组解的搜索，能够实现对布尔方程组求解的二次加速，并通过改进和优化算法的线路，实现比特资源和线路深度的优化，从而发挥量子计算机的最大潜力。

2背景知识

2.1布尔方程组

用 F2表示只包括元素0和1的二元域，用 F2（n） 表示二元域 F2={0，1}上的 n 维向量空间，用+和∑i表示实数中整数的加法，用和i表示实数中整数的模2加法，同时用表示 F2（n） 中向量的加法。因为 F2（n）中的向量与[0，2n-1]的整数之间存在自然的一一对应关系，所以可以按照它们对应整数从小到大的顺序来排列Vn中的向量，并且记：

为了方便计算，F2（n） 中的向量αi同时表示它对应的整数i，从 F2（n） 到 F2的映射f（ x）称为 F2（n） 上的布尔函数，其中 x ∈F2（n） 。布尔函数f（ x ）可以唯一表示成 n 个变量的多项式，即：

其中，x=（ x1，…，xn ）∈F2（n） ，u=（ u1，…，un ）∈F2（n） ，λu ∈ F2。这种表示称为 f（ x ）的代数式（ Algebraic NormalForm，简称为 ANF），多项式中的每一项∏i（n）=1 x i（u）i称为f（x）的单项式（Monomial），它的次数定义为其中不同变量的个数，而f（ x）的所有单项式次数的最大值称为布尔函数f（x）的代数次数，记为 deg（f）。

F2（n） 上次数小于或等于1的布尔函数称为仿射函数，它们具有如下形式：

其中，ai ∈F2，i=0，1，…，n。特別地，a0=0，该仿射函数称为线性函数。一般地，分别用 An 和 Ln 表示 F2（n）上所有仿射函数和线性函数的集合。

2.2 Grover 算法

给定一个集合 X，元素数目是 N，函数映射是f：X

其中，T 是要找到的目标解的集合，元素数量是 t。 Grover 算法是一个需要重复应用下面的操作多次的算法。

式（5）被称为 Grover 迭代。对任意的初态|Ψ）= A |0），有：

式（6）中，H  n 是一个 Hadamard 算符的集合，|τ）是一个由所有目标态构成的一个等概率叠加态构成的态。

S0和 Sf 的作用分别是将态|0）和态|τ）进行翻转。其中，Sf 和-AS0A-1分别被称为黑盒和振幅翻转操作。

通过将黑盒作用到初始态上，只有目标态的振幅发生反转，被标记。振幅翻转操作将振幅按照均值进行翻转。测量的成功概率是关于迭代次数的函数，已被研究[15]，最佳的迭代次数可以让成功的概率最大化。通过应用 Q 在初始态上i?次，找到这 t 个目标解的概率表示为pt N：

其中，sin（θt，N ）==（Ψ∣τ））。让成功概率最大化需要的 Q 的重复次数可表示为 I ∈N，I=·

3 Grover 算法优化方法

综上可知，Grover 算法主要分为两个部分，即量子黑盒运算和相位翻转运算。布尔方程的计算只包含布尔加法“+”和乘法“×”，对应到逻辑门操作为异或（ xor）和与（ and）。在量子黑盒中，xor运算可以用量子非门 x 实现，and 运算可以用量子toffoli门 ccx 或者多比特控制门 mcx 实现。

求解 n 个变元的方程组的线路理论需要的总比特个数为2n+1，每表示一个变元需要一个量子比特，共需要 n 个量子比特;由于量子计算过程是可逆的，所以量子黑盒还需要增加一些辅助比特存储计算结果。每表示一个方程需要一个辅助比特，共需要 n 个辅助比特;最后还需要一个辅助的标记比特位，因此共需要2n+1个量子比特。但是，由于种种原因，目前不论是模拟器还是量子计算机，能够使用的比特数量是有限的，同时支持的线路深度也是有限的。因此，本文提出了一种 Grover 算法的线路优化方案，该方案包含两个方面。

（1）优化线路深度。理论上，Grover 算法的迭代次数为解空间的开根号级别，此时可以以接近1的概率得到正确解，但是这样的线路深度执行起来有难度。为了降低线路深度，应用精度换深度的思想，启发式的选用一个远小于理论值的迭代次数（p× n），同时将最优解限定在前 m 个概率最高的结果中，最后在这20个高概率的结果中寻找正确解。这种回代验证的方式代价是很小的，实现了用较小的精度确损失换来深度的大幅减少。

（2）优化线路比特资源。求解 n 个变元的方程组的量子门线路理论需要的总量子比特个数为2n+1。表示变元的量子比特数目是无法改变的，因此将优化目标放在了辅助比特上。为减少需要的辅助量子比特数，设计了辅助比特重复利用的思想，在使用过一些辅助量子比特后，再将其还原至初始状态，随着 n 的增加，总结规律可知辅助比特数量满足1+2+…+k<=n，满足此不等式的最小 k 值，即为（  ），此时辅助比特只需要 n+1+（  ）。不难看出，（  ）< n（ n>2），需要的量子比特数减少。

4实验和结论

4.1案例实验

以3变元的方程组为例，方程组如下：

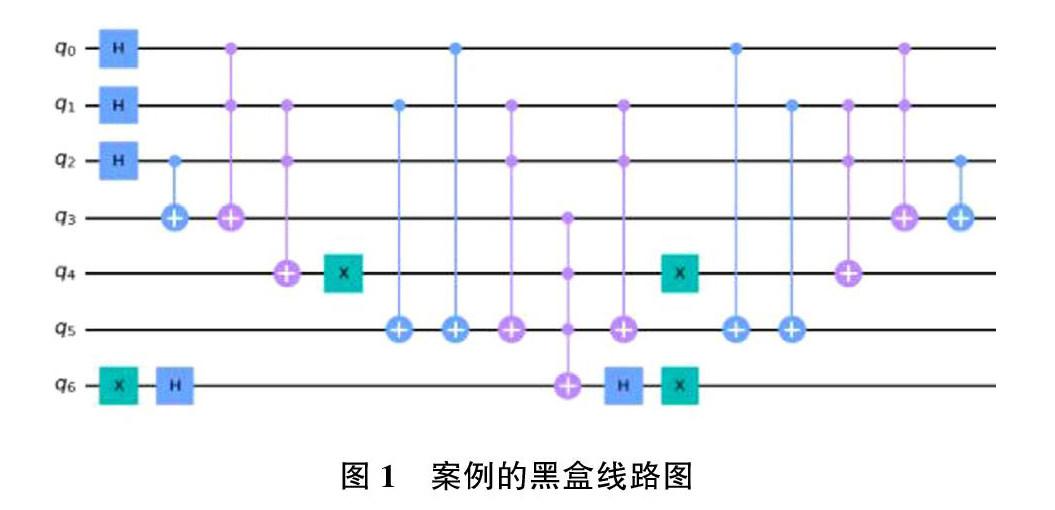
由于变元是3个，因此需要量子比特 q0，q1和 q2表示变元 x1，x2和 x3。黑盒构造参照之前提到的方法，以其中一个方程 x1x2+x3=1举例，x1x2是乘法对应的是 ccx 门，同时需要辅助比特 q3保存结果，x3和 x1x2是xor关系，因此将 x3和 x1x2结果应用量子非门。基于此，将第一个方程的计算结果保存在量子比特 q3上。依次类推，即可表示每个方程，共需要7个量子比特。最后，根据 Grover 算法，用额外的一个辅助比特位标记所有的方程的正确解。三个方程之间是 and 的关系（ x1x2+x3）^not（ x2x3）^（ x1+x2+x2x3）=1，因此用的是 mcx 门实现标记。对应的黑盒线路如图1所示。

因为量子计算是可逆的，同时为了后面算法迭代，需要将线路中辅助量子比特还原，通过对称作用相同的门，即可实现。相位翻转是 Grover 算法的一个固定的结构，需要的比特数和变元数一致，即如图2所示。

根据 Grover 算法给出的理论最佳迭代次数是 pi/4×sqrt（8）～=2。结果是101，为正确解，概率是95%，接近1。线路深度是45。图3和图4分别为 Grover 求解线路图和 Grover 求解结果图。

4.2案例优化

按照之前的分析，线路深度优化方面，选用一个远小于理论值的迭代次数（0.5× n）=1。测量概率较高的前几个结果，并带回验证是否是正确解。同时，按照比特重复利用思想，量子比特的数量是 n+1+（  ）=6。优化的线路和结果如图5和图6所示。

不难发现，优化后的线路深度是24。在概率较高的3个结果（011、100、101）中，通过带回验证发现，解101就在其中。这也就证明了通过精度换深度的思想是可行的。此外，测试了全部的不超过28变元的方程组，归纳得到一个远小于理论值的迭代次数（0.5×n），同时在前 m（ m<20）个概率最高的结果中寻找最优解。同时，发现比特数量的增加比线路深度的增加带来的时间复杂度更高这一结论，因此优化比特数量更重要。

5分析讨论

对于方程组，特别是非线性布尔方程组的求解问题，基于 Grover 搜索算法是一种可行的量子解决方案，在求解过程中，可以利用精度换时间及量子比特复用的技术实现线路深度和量子比特数的减少，可在更多的应用中发挥作用。另外，受限于当前的量子计算机的资源和深度，这种以理论为参考、启发式的工程实现方案是一种不错的选择，同时对已知线路的优化都可极大地激发当前量子计算机的计算潜力。

参考文献：

[1]刘连浩，段绍华，崔杰.一种基于Grobner基的代数攻击方法[J].计算机工程，2008（16）：157?158+167.

[2] Faugere J C，JouxA.Algebraic cryptanalysis of hidden field equation （ HFE ） cryptosystems using Grbner bases [ J ]. Springer，2003：1?17.

[3]左鑫平，李俊全.一种改进的 XL 算法[ J].计算机工程，2008，34（19）：157?159.

[4]张帆，李蕾，熊炎.XL 算法的冗余分析与改进[ J].计算机工程，2011，37（16）：60?61+64.

[5] Strang G.Introduction to Linear Algebra [ M ].Wellesley? Cambridge Press Wellesley，2016.

[6] CHEN Y A，GAO X S.Quantum Algorithm for BooleanEquation  Solving  and  Quantum  Algebraic  Attack  onCryptosystems [ J ]. Journal  of  Systems  Science  and Complexity，2021，35（1）：373?412.

[7] Grover L K.Quantum Mechanics Helps in Searching for aNeedle in a Haystack[ J].Physical Review Letters，1997，79（2）：235.

[8] LONG G L，LI Y S，ZHANG W L，et al.Dominant gateimperfection in Grover，s quantum search algorithm [ J ]. Physical Review A，2000，61（4）：042305.

[9] CHUANG I  L， KUBINEC  M ， GERSHENFELD  N.Experimental implementation of fast quantum searching[J].Physical review letters，1998，80（15）：3408?3411.

[10] ZALKA C.UsingGrover，s quantum algorithm for searchingactual databases ? art.no.052305[J].Physical Review，A，2000，62（5）：2305?01?2305?04.

[11] YAMASHITA S.How to utilize a Grover search in general programming[ J].Laser Physics： An International Journaldevoted to Theoretical and Experimental Laser Research andApplication，2006，16（4）：730?734.

[12]阮越，陈汉武，刘志昊，等.量子主成分分析算法[ J].计算机学报，2014，37（3）：666?676.

[13] PENG H，JING J.Research on routing algorithm of Grover for wireless ad hoc quantum communication network[J].Journal of Zhejiang University of Technology ，2014，42（6）：612?615.

[14] SUN G D，SU S H，XU M Z.Quantum mechanical algorithms for solving root finding problem [ J ].Journal of Beijing University of Technology，2015，41（3）：366?371.

[15] Boyer M，Brassard G，H?yer P，et al.Tight Bounds onQuantum Searching [ J ].Fortschritte der Physik，1998，46（4?5）：493?505.

作者简介：

钱宇梁（2001—），本科，研究方向：量子计算和量子机器学习。