热结构耦合状态下盘式制动器材料参数对耦合场的影响

2022-04-29张雪松王兆恒王长通

中原工学院学报 2022年1期

张雪松，王兆恒，王长通

(1.中原工学院机电学院，河南郑州 450007； 2.郑州经贸学院机械工程系，河南郑州 451191；3.中原工学院学报编辑部，河南郑州 450007)

制动器是现代汽车必不可少的一部分，它能通过自身摩擦组件的摩擦作用产生制动力，实现对车辆运行速度的控制。盘式制动器主要由制动盘、摩擦片、支架、液压油缸等组成。制动器制动过程中摩擦片与制动盘的摩擦和冲击作用往往会导致制动噪音的产生，而制动噪音产生的直接原因在于制动器内部失衡导致的振动。制动器的制动是一个热应力与结构应力耦合作用的过程，制动盘受到摩擦片的挤压后产生一定的结构应力，同时制动盘与摩擦片的摩擦过程会产生大量的摩擦热而导致制动器温度的的急剧升高，进而对制动器的机械结构产生影响，使制动盘与摩擦片发生一定程度的变形，制动器内部应力的分布受到影响。关于汽车制动器制动过程的大量研究表明，摩擦副内部的接触形态对制动器的稳定性有重要影响，制动过程中制动器内部热应力与结构应力的应力集中问题直接关系到系统模态的稳定，会导致不稳定模态增多、模态不稳定系数增大，具有引起强烈尖叫的倾向[1]。制动器各零部件的材料参数对其内部应力场的分布有一定的影响。朱爱强等采用有限元分析方法，对6组不同材料组合的制动盘与摩擦片温度场进行分析，得出了不同材质对制动盘温度场的影响，其中同类材料中密度越低，摩擦温升就越小，温度场的分布也就越均匀；同时，得出了材料比热容与热导率对温升有一定影响的结论[2]。徐伟等通过6组自定义的不同材料，对盘式制动器接触应力分析后指出，接触应力是影响摩擦副热流密度的直接因素[3]。从文献[3]可知：在其他参数不变的条件下，材料的弹性模量会直接影响接触应力的分布，过大的弹性模量易造成应力集中；减小热流参数值和热膨胀系数，可改善摩擦副的应力分布。姚冠新等采用Abaqus有限元分析软件模拟了制动器制动过程的瞬态温度场，通过只改变比热容和导热系数中某一个参数的值进行分析，得出了以下结论：在其他条件不变的情况下，比热容的增大可减小制动器的温升，但会导致制动器径向和轴向温度梯度的增大；导热系数则与比热容的影响相反，且在相同的条件下，比热容对温度场的分布影响大于导热系数[4]。综上所述，已有文献中不乏对单一参数影响制动器温度场和应力场进行的研究，但针对材料参数中的单一变量对制动过程中热结构耦合场影响的研究尚无先例。本文将通过制动器材料的弹性模量、导热系数和热膨胀系数等参数的变化，对制动器制动过程热结构耦合场的应力分布进行探讨，并进一步评估制动器模态受到的影响。

1 热结构耦合理论

对制动过程的热结构耦合分析，需要同时考虑热应力、结构应力的影响以及两者之间的相互作用。制动力在产生结构应力的同时会产生摩擦热，而摩擦热会导致制动器的升温变形，从而改变摩擦副的接触形态，影响结构应力的分布。设制动器的体积为V，边界条件为S，则根据文献[5-10]可列出下列能量守恒方程：

(1)

制动器的应力平衡方程为：

(2)

边界力又称制动压力，可表示为：

Pi=niσij

(3)

式中：ni为制动器表面的单位向量；σij为柯西应力分量。

将式(3)代入式(2)，并进行整理，所得为制动器的热结构耦合能量守恒方程，即

(4)

式中：ρij为耦合场的结构密度。

根据虚功原理，制动器的结构位移u需满足的条件为：

(5)

式中：δui为虚位移；xi为节点i的位移；bi为插值向量。

节点位移矢量u(t)需满足的条件为：

(x,t)=N(x)u(t)

(6)

式中：(x,t)为节点x在t时刻的坐标；N(x)为形函数矩阵。

温度场的关系式为：

Tm(x,t)=T(t)B(x)

(7)

式中：T(t)为节点的温度矢量；B(x)为温度场的插值函数；Tm(x,t)为节点x在t时刻的温度值。

应变矩阵ε(x,t)的表达式为：

ε(x,t)=B(u)u(t)

(8)

式中：B(u)为位移场的插值函数。

根据式(4)-式(8)推导，所得温度场的有限元方程为：

(9)

应力应变场的有限元方程为：

(10)

式中：Ku为力学刚度矩阵；MT为热刚度矩阵；F(t)为载荷矢量。

将式(9)和式(10)合并，可得：

(11)

2 制动器的建模与仿真

2.1 盘式制动器建模

本文以某型量产乘用车的盘式制动器作为研究对象，进行建模与仿真。盘式制动器制动过程产生的噪音主要来源于制动盘与摩擦片接触的振动。为了提高计算效率并降低网格划分的难度，同时保证仿真计算的准确性，本文建模时在确保制动盘、摩擦片等核心结构(结构的主要尺寸如下：制动盘外径为330 mm，内径为150 mm，厚度为24 mm；摩擦片外径为308 mm，内径为220 mm，厚度为14 mm，包角为60°)不变的条件下，对制动器的其他部件进行简化，并将三维结构中的圆角、倒角等删去。

将简化后的装配体模型导入ANSYS Workbench软件，并选定仿真所用材料。其中摩擦片为树脂基复合材料，制动盘和其余部件的材料均为灰铸铁HT250。将选定材料分别赋予相应部件，并对模型进行网格划分。通过单元质量、单元纵横比和雅可比等参数判断发现，网格划分的效果良好。盘式制动器装配体模型的有限元网格划分结果如图1所示。它共有80 719个单元，138 026个节点。

图1 盘式制动器装配体模型的有限元网格划分结果Fig. 1 Meshing diagram of disc brake assembly model

2.2 仿真与材料参数设置

本文首先通过ANSYS Workbench软件进行盘式制动器的热结构耦合分析，采用间接耦合的方法，在工程数据库中完成制动器材料参数的定义；其次，将材料参数导入瞬态热分析模块，在热分析模块中进行制动盘摩擦接触区域的分割，并对其施加热流载荷，设置热力学参数、支撑以及位移限制等边界条件，进行瞬态热求解，完成第一次热应力分析；然后，将瞬态热求解的结果导入静态结构分析模块，作为热结构耦合求解的已知条件，同时施加制动压力5 MPa，并对结构分析模块进行设置，通过有限元计算完成热结构耦合分析；最后，将耦合场的分析结果导入模态分析模块，进行制动器的模态分析，得出仿真结果。热结构耦合模态分析流程如图2所示。

图2 热结构耦合模态分析流程Fig. 2 Flow chart of thermal-structure coupling modal analysis

大量研究表明，制动噪音的产生主要归根于制动盘的振动，高速旋转的制动盘对制动器的稳定性具有十分重要的影响[11]。为了探究制动盘材料的弹性模量、导热系数和热膨胀系数对制动盘热应力和结构应力耦合场的影响，现以灰铸铁HT250的基本参数为依据，采用单一变量法，将上述材料参数按不同条件设置并分为7组(见表1)进行仿真。其中：组别1-3为HT250材料弹性模量依次递增的设置，用于对比不同弹性模量下耦合场的应力极值和应力集中程度，研究弹性模量对热结构耦合场的影响；组别4-5、组别6-7采用方法与组别1-3相同，但分别为导热系数和热膨胀系数的相应设置。

表1 仿真分组与参数设置Tab. 1 Grouping and parameter setting of the simulation

3 仿真结果及分析

对比不同材料参数的7组仿真结果，可得出某一特定参数改变对制动器热结构耦合场的影响；结合模态分析结果，可判断该参数对制动器模态的影响。

3.1 弹性模量对温度场和耦合场的影响

材料参数组别1-3的仿真温度场云图如图3所示。

(a) 组别1

(b) 组别2

由图3可看出：对应于弹性模量为1.05×1011Pa的组别1，制动盘的最高温度为94.737 ℃；对应于弹性模量为1.55×1011Pa的组别2，制动盘的最高温度为82.251 ℃，且相对于组别1，其温度场云图中的高温区域的面积明显较小；对应于弹性模量为2.05×1011Pa的组别3，制动盘的最高温度为82.142 ℃，温度场云图与组别2的情况基本相同。由此可见，制动盘的弹性模量对制动过程的温升有一定影响，随着弹性模量的增大，其温升呈下降趋势，且温度场的热力集中现象有所缓解，制动盘的温度场状态趋于稳定。

材料参数组别1-3的仿真热结构耦合应力云图如图4所示。

(a) 组别1

(b) 组别2

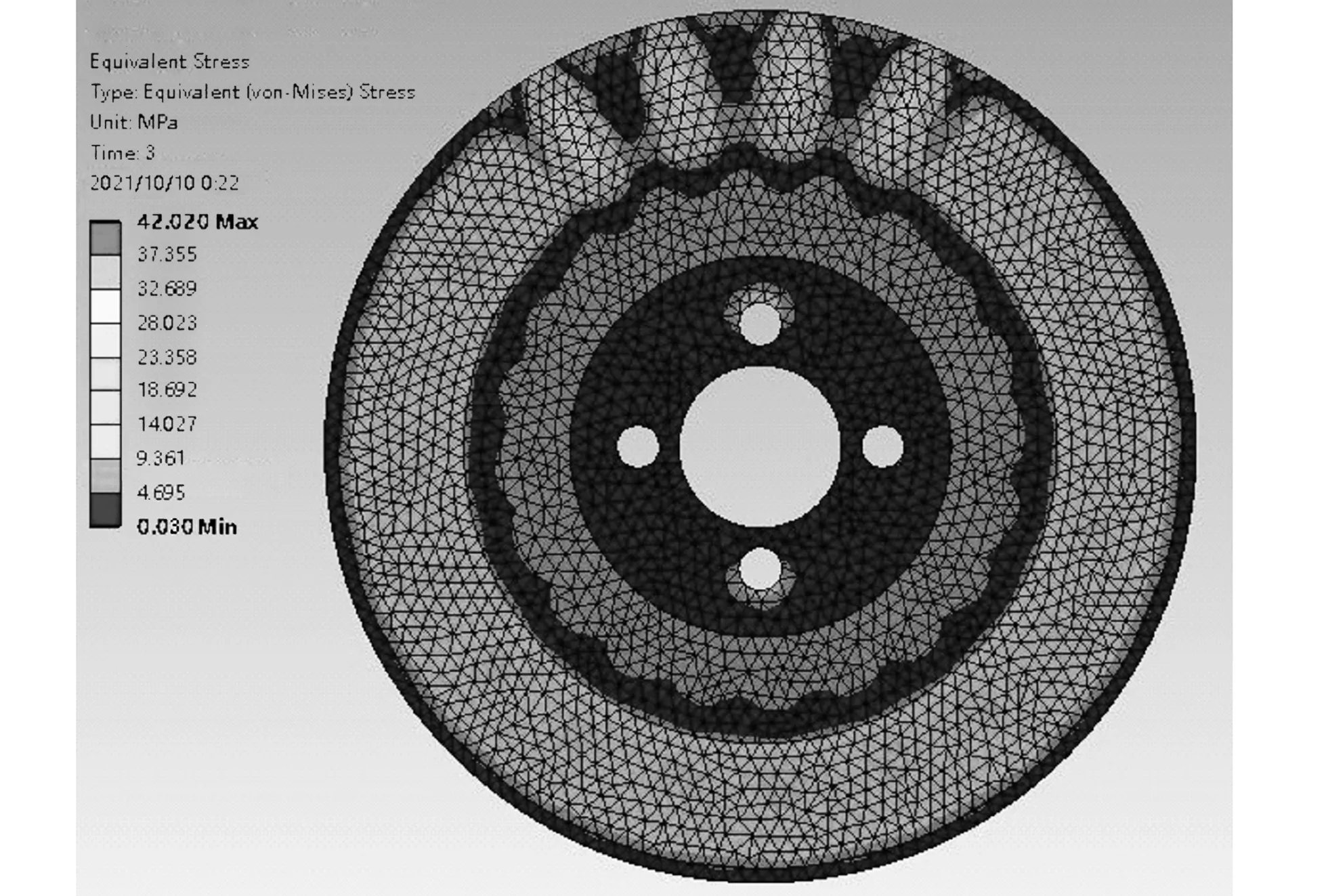
(c) 组别3图4 材料参数组别1-3的仿真热结构耦合应力云图Fig. 4 The group 1-3 cloud diagrams of coupled stress field of simulated thermal-structure

由图4可看出：组别1-3的最大应力分别为23.248 MPa、40.731 MPa和42.020 MPa；图4(a)中最大应力区域较为均匀地分布在制动盘的整个外表面，且其盘面的应力分布表现为，从整体上以最大应力环面为中心向四周辐射状减小的态势；图4(b)、图4(c)中应力分布特点与图4(a)有较大不同，其中最大应力出现在制动盘通风孔之间的加强肋上，且与摩擦片直接接触区域的应力集中现象更加突出，在摩擦片接触区与制动盘的安装台之间出现了局部区域应力分布情况与图4(a)情况相反的结果，在紧贴摩擦区出现了一定范围的最小应力区域。研究发现，随着制动盘弹性模量的升高，制动过程的耦合应力可增大至原有应力的2倍左右，且其应力集中现象更加明显。

综合上述分析可知：随着制动盘弹性模量的升高，在制动压力相同的情况下，制动盘的弹性形变减小，故摩擦副的接触面状态有所改善，使得制动温升减小，但应力集中现象却更加突出；制动盘的变形量减小，刚度增大，导致制动器的各阶固有频率升高，低频稳定性有所提高。仿真所得材料参数组别1-2的制动器各阶固有频率如图5所示。

图5 材料参数组别1-2的制动器各阶固有频率Fig. 5 Schematic diagram of natural frequencies of each order of group 1-2 simulated brakes

3.2 热参数对制动过程温升和应力分布的影响

为了更加直观地表达制动盘的温度变化，对材料参数组别1和组别4-7的仿真结果进行整理，可得图6所示不同材料参数下制动盘在制动过程的温度变化。

(a) 不同导热系数

(b) 不同热膨胀系数图6 不同材料参数下制动盘制动过程的温度变化Fig. 6 Effect of different thermal parameters on brake disc brake temperature change

由图6(a)中材料参数组别1与组别4、组别5的温升对比可发现，在整个制动过程中，不同导热系数的制动盘的温升趋势基本相同，其中组别1温升最大，随着导热系数的增大，制动盘的温升呈下降趋势，组别4和组别5的最高温度分别为81.67 ℃与75.13 ℃。由图6(b)中材料参数组别1与组别6、组别7的温升对比可发现，在整个制动过程中，热膨胀系数的改变对制动盘温升的影响与导热系数的影响相反，随着热膨胀系数的增大，制动盘的最高温度也随之增大，组别6和组别7的最高温度分别为102.55 ℃和113.67 ℃，且相较于组别1来说，组别6、组别7的制动盘降温曲线的斜率更大，即降温速率大于组别1。

(b) 不同热膨胀系数图7 不同材料参数对制动盘应力分布的影响Fig. 7 Effect of different thermal parameters on stress distribution of brake disc注：各组别中从左到右的柱状图形(若图形数量足够的话)对应的应力依次为15 MPa以下、大于等于15 MPa而小于20 MPa、大于等于20 MPa而小于25 MPa、大于等于25 MPa。

为了对比材料参数改变后制动盘应力集中的程度，本文以耦合应力的分布为依据，将耦合应力分为15 MPa以下、大于等于15 MPa而小于20 MPa、大于等于20 MPa而小于25 MPa、大于等于25 MPa 4档，并根据热结构耦合应力云图计算了不同档应力分布所对应区域的面积占整个盘面的百分比。不同材料参数对制动盘应力分布的影响如图7所示。

组别4和组别5的最大应力分别为19.36 MPa和17.68 MPa，均低于20 MPa，而组别6和组别7的最大应力分别为25.12 MPa和26.98 MPa，均高于25 MPa；相较于组别1，组别4、组别5的应力范围更小且各档占比更加均匀，而组别6、组别7的应力跨度更大，且各档应力分布区域的面积占比相差明显。分析可知：随着导热系数的增大，制动盘在制动过程中的应力分布更加均匀，应力集中现象得到缓解，而热膨胀系数的增大则加剧了制动盘的应力集中现象，使制动器的稳定性变差；同时，热膨胀系数的增大，使得制动盘的变形增大，制动盘与摩擦片的接触应力变大，产生更多的摩擦热而导致其温升加剧。