GPS-IR用于验证3种海潮模型及其在近海区域的精度分析

武慧琳 张双成 尹 彤 张伟琪

(1.自然资源部测绘标准化研究所 陕西西安 710054；2.长安大学 陕西西安 710054；3.自然资源部第一大地测量队 陕西西安 710054)

沿海地区是一个国家的经济中心和交通枢纽，地势平坦，人口稠密，工农业发达，对于建立GNSS基准站具有得天独厚的区位优势。但是沿海地区地处潮汐作用带，常年受到潮汐作用的影响，会直接或间接地给人们的正常生产生活造成一定的影响，甚至会对人民的生命财产造成威胁[1]。因此，深入认识潮汐的规律，研究海岸和河口潮汐规律至关重要。调和分析法是潮汐分析和预报的主要方法之一，由调和分析得到的调和常数是海岸及河口潮汐的一个重要特征参数，在潮汐预报和潮汐表编制等过程中起到了关键作用[2-3]。

1980年，Schwiderski等首次将动力学方程和全球范围内的2 000多个验潮站实测数据相结合，对Laplace潮波方程做了拓展，建立了首个全球海洋潮汐模型。然而由于潮位资料匮乏，所建立的模型的潮波系数极不稳定，误差较大[4]。近年来，卫星测高技术的发展极大地推动了海洋潮汐的研究[5-6]，许多学者利用验潮站资料和卫星测高资料构建了一些精度较高的全球海潮模型，如NAO.99B、FES2004、SCW80和TPXO模型等。

当前，许多学者还在全球海潮模型精度评估方面开展了大量的研究工作，并取得了丰硕的成果。李大炜等[7]利用传统验潮站数据对5个全球海洋潮汐模型(NAO99b、FES2004、GOT4.7、TPXO7.2 和EOT10a) 进行了精度评估。结果表明，EOT10a 模型在全球海洋范围综合指标最优，能较好地反映全球海洋潮汐的分布。付延光等[8]基于验潮站资料对比分析了3个全球海潮模型(DTU10、TPXO7.2、NAO99b)和1个区域海潮模型(NAO.99Jb)在中国沿岸的准确度。结果表明，NAO.99Jb在中国海域精度最高，TPXO7.2次之。孙佳龙等[9]基于验潮资料分析了CSR4.0模型和NAO.99b模型在中国海域的精度，得出在中国近海区域CSR4.0模型的平均精度比 NAO.99b模型精度高。以上这些学者都是基于传统验潮站数据对海潮模型进行的研究分析，但由于验潮站在全球或区域的数量有限，且时空分辨率较低，因此对GNSS-IR技术的研究很有必要。

随着对GNSS的研究及应用的不断深入，基于多路径效应的GNSS-IR技术已成为一种新兴的潮位监测手段[10-12]。当前，各国相继在沿海区域布设GNSS基准站，我国也在无验潮站的沿海地区布设了一定数量的GNSS基准站，进一步促进了GNSS-IR技术的发展。沿海GNSS基准站在一定程度上可以作为常规验潮站的有效补充。目前已有大量的研究表明，GNSS-IR技术用于海平面变化监测的精度正逐步提高，但是将该技术用于获取潮波系数及其海潮模型的研究却相对较少。本文利用布设在美国华盛顿州的GPS基准站(SC02站)实测数据进行了相关试验，即用验潮站资料获取的潮波系数来验证GPS-IR(Global Positioning System Interferometric Reflectometry)获取的潮波系数的准确性，并将其与TPXO6.2、TPXO9和DTU10海洋潮汐模型获取的潮波系数进行分析比较，以验证GPS-IR技术的有效性和可靠性。

1 GPS-IR潮位监测及潮波系数提取原理与全球海潮模型

1.1 GPS-IR潮位监测及潮波系数提取原理

多路径效应是GNSS应用中的主要误差源之一，不同路径的信号相互间发生干涉，产生了多路径效应，导致测量精度有所降低。当GPS基准站位于海水面附近时，GPS卫星接收到的信号实际是直射信号Ad与经海水面反射的信号Am的合成干涉信号[13]。利用GPS-IR技术探测潮位变化的原理如图1所示。

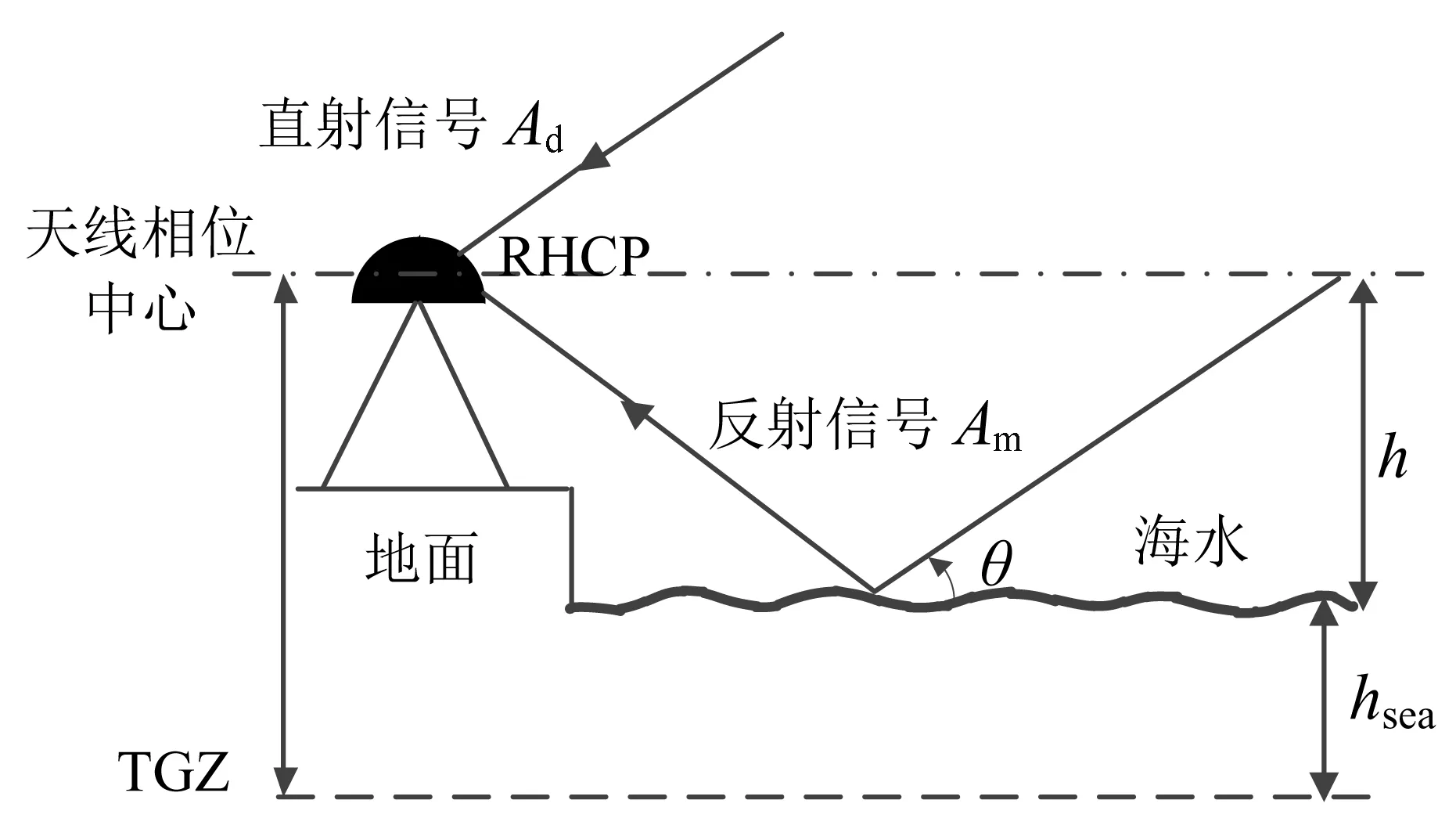
图 1 GPS-IR探测潮位变化示意图Fig.1 Schematic Diagram of GPS- IR Detecting Tide Level Changes

图1中，h为垂直反射距离，即天线相位中心到瞬时潮位的距离，θ为直射信号和瞬时潮位的夹角，hsea为基于海面参考基准的海面高度，TGZ为验潮仪的基准起算面，RHCP为单天线。

对于测量型GPS接收机天线而言，直射信号的振幅大于等于反射信号的振幅，即Ad≥Am，表示GPS接收机捕获的合成信号Ac中，直射信号Ad决定着合成信号的总体变化趋势，而反射信号Am则表现为局部的周期性震荡，这主要是受低高度角多路径影响所致，可通过二次多项式拟合方法来分离直射信号和反射信号。信号振幅与信噪比(SNR)的关系可以表示为[14]

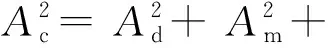
(1)

分离后得到的反射信号的振幅可表示为

(2)

式中：λ为卫星信号的波长，E为卫星高度角，A为振幅，h为垂直反射距离，Φ为相位。

若计t= sinE，f= 2h/λ，则式(2)可表示为

Am=Acos(2πft+ Ф)

(3)

垂直反射距离h是频率f的函数，sinE是随高度角变化的已知量，但由于sinE是非等间隔采样，导致SNR残差序列无法保证正周期截断。因此，本文采用Lomb-Scargle(L-S)谱分析方法获取频率数据。

实际海洋潮位可以表示为一系列余弦项在某一固定值上的叠加[15]，用公式表示为

(4)

式中：h0为平均海面；α为海面变化的趋势项；r为余差或观测噪声；σ为分潮的角速度；t为参考时间；V0为分潮流速；fi、u分别为月球轨道18.6年变化引入的平均振幅H和相角的修正值；实际潮汐分潮的调和常数Hi表示分潮的振幅，调和常数gi表示的是格林尼治迟角，二者反映了海洋对这一频率外力的响应；-gi为实际分潮相对引潮力分潮的位相超前。

在实际调和分析中，潮位可表示为

式中：Ci=Hicosgi，Si=Hisingi。

对式(5)进行调和分析，可得到各分潮的Ci和Si，从而得到分潮的振幅和迟角[15]为

(6)

根据GPS-IR潮位监测及潮波系数提取原理，不同数据源潮波系数提取分析的具体流程如图2所示。

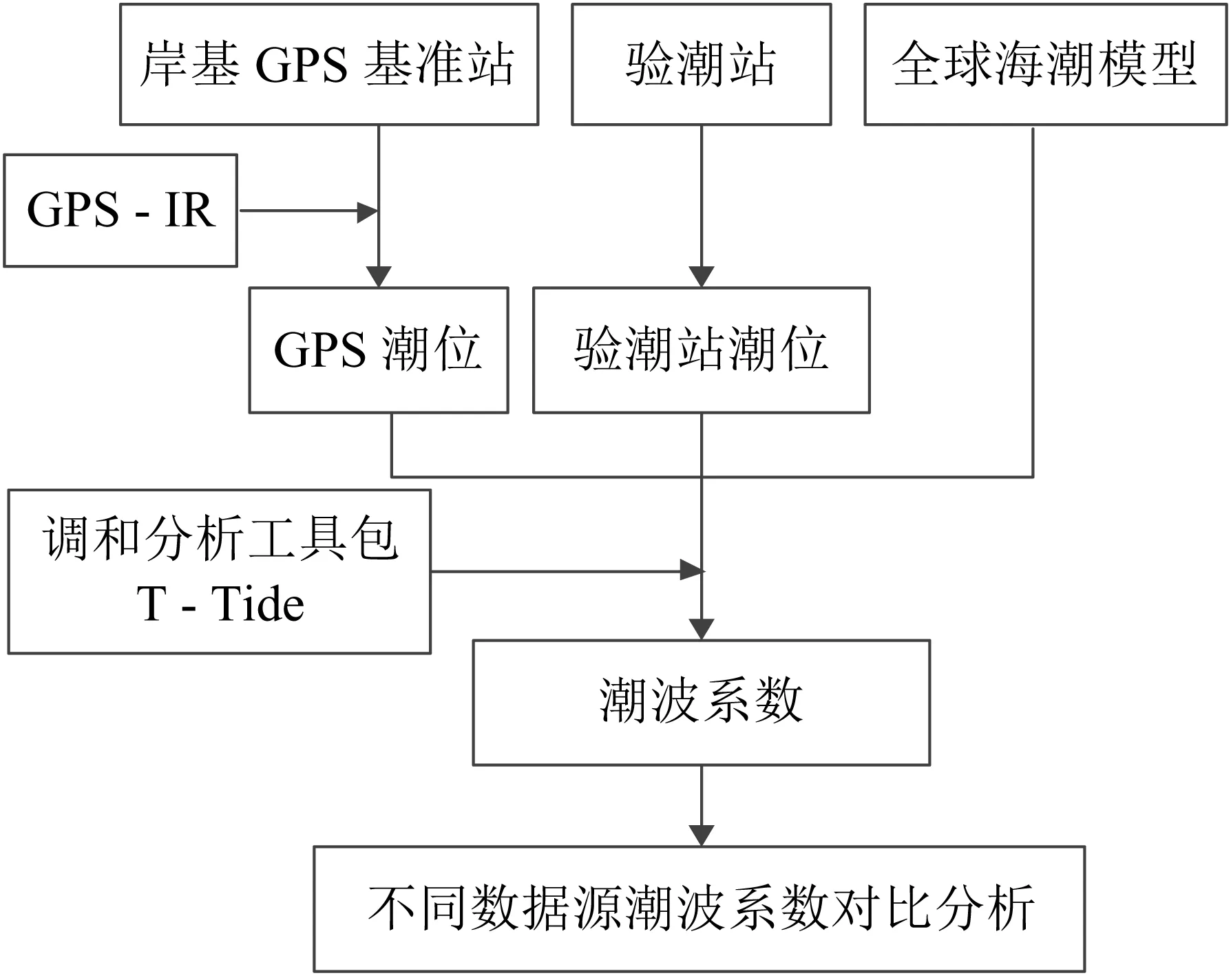
图2 不同数据源潮波系数提取分析流程Fig.2 Extraction and Analysis Process of Tidal Wave Coefficients of Different Data Sources

1.2 全球海潮模型

全球海潮模型在确定海平面、海底地形和深度基准面等方面有着重要的作用。其中，全球海潮模型DTU10在近海区域相对准确，而TPXO系列模型由于利用了大量的卫星测高数据，因此有着更高的空间分辨率。本文选取TPXO6.2、TPXO9和DTU10这3种有代表性的全球海潮模型进行分析，模型基本信息如表1所示。

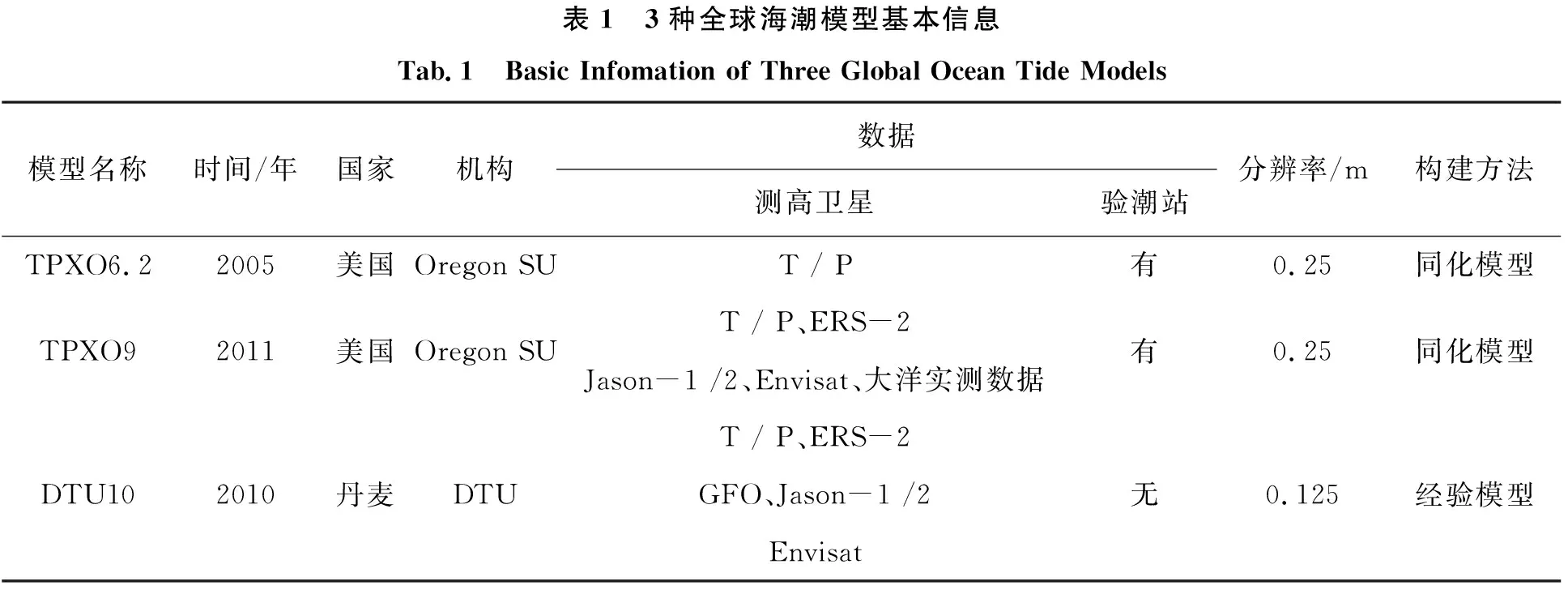
表1 3种全球海潮模型基本信息Tab.1 Basic Infomation of Three Global Ocean Tide Models模型名称时间/年国家机构数据测高卫星验潮站分辨率/m构建方法TPXO6.22005美国Oregon SUT / P有0.25同化模型TPXO92011美国Oregon SUT / P、ERS-2Jason-1 /2、Envisat、大洋实测数据有0.25同化模型DTU102010丹麦DTUT / P、ERS-2GFO、Jason-1 /2Envisat无0.125经验模型

2 利用GPS-IR技术获取潮波系数的精度分析

2.1 数据来源

为了验证GNSS-IR技术获取潮波系数的精度，本文选用属于美国地球透镜计划(Earth Scope)PBO网络的SC02站的观测数据进行试验分析。SC02站位于北美华盛顿州港湾，并且布设在海岸边，监测环境开阔，能接收较大范围内来自海面的反射信号。SC02站所采用的接收机为TRIMBLE NETR9大地测量型接收机，GPS天线为天宝公司带整流罩(SCIT)的扼流圈天线(TRM59800.80)。该站已有10多年的连续观测数据，数据完整性良好，而且可以采用距离SC02站359 m的Friday Harbor验潮站的实测数据进行对比分析。Friday Harbor验潮站建设于1934年，是由美国NOAA(National Oceanic and Atmospheric Administration)的海洋产品和服务中心建设维持的连续运行验潮站，在1996年配备了Aquatrak公司的声学验潮仪，可以提供采样间隔为6 min的潮位数据。图3是SC02站GPS站点的位置分布图，其反射高度为4 m，射线部分显示的是仰角为5°、8°和12°的菲涅耳反射区域。

图3 SC02站菲涅尔反射区Fig.3 Fresnel Zones of Station SC02

2.2 试验分析

目前已有的大量研究表明，低高度角受多路径影响较为严重，因此本文选取高度角范围为5°～12°、方位角范围为50°～240°的信噪比数据进行试验分析。本文利用2017年7月(第193天到第199天)SC02站获取的L1信噪比数据，按照不同数据源潮波系数提取分析流程获取了潮位数据，并与Friday Harbor验潮站的数据进行对比。结果表明，GPS-IR获取的潮位数据与验潮站观测潮位数据的较差均值为 10.4 cm，差值的RMS为11.4 cm，相关系数为0.972，一周潮位变化对比如图4所示。

由图4可以明显看出，GPS-IR反演潮位结果与验潮仪观测结果基本一致，但仍有个别结果存在偏差，原因主要与海面波浪急剧变化和所采用的粗差剔除方法有关。为验证GPS-IR技术反演潮位变化的有效性和连续性，以及GPS-IR获取潮波系数的精度，本文选取GPS测站(SC02)和Friday Harbor验潮站2005—2017年共计13年的数据进行试验。结果表明，GPS-IR获取的潮位结果与验潮站观测结果的较差均值为2.93 cm，差值的RMS为3.57 cm，相关系数为0.985。GPS-IR技术反演潮位与Friday Harbor验潮站实测潮位的对比结果如图5 所示。

图4 一周潮位变化对比Fig.4 Contrast of Tide Level Changes in a Week

从图5中可以明显看出，GPS-IR获取的潮位数据和验潮站的实测潮位数据的整体趋势具有较好的一致性，但反演结果仍在部分时刻存在异常，这可能与采用二阶多项式去除趋势项，以及高度角选取范围没有进一步细化有关。

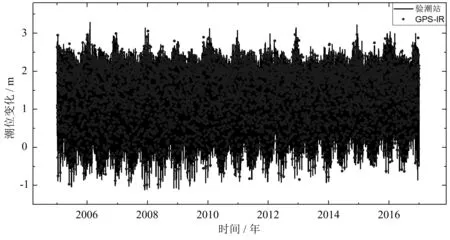
图5 GPS-IR反演潮位与验潮仪实测潮位对比Fig.5 Contrast of Tide Level Retrieved by GPS- IR and Tide Level Measured by Tide Gauge

已有相关研究表明，要得到准确、稳定的潮波系数，一般需要18.6年以上的验潮数据，但是由于SC02测站数据的时间跨度不够长，且测站坐落在浅水区域，所以存在大量非线性的复合潮。调和分析结果显示， Friday Harbor验潮站振幅大于1 mm的潮汐成分有102个，本文列举了其中9个较大分潮的潮波系数统计信息[14]，见表2。

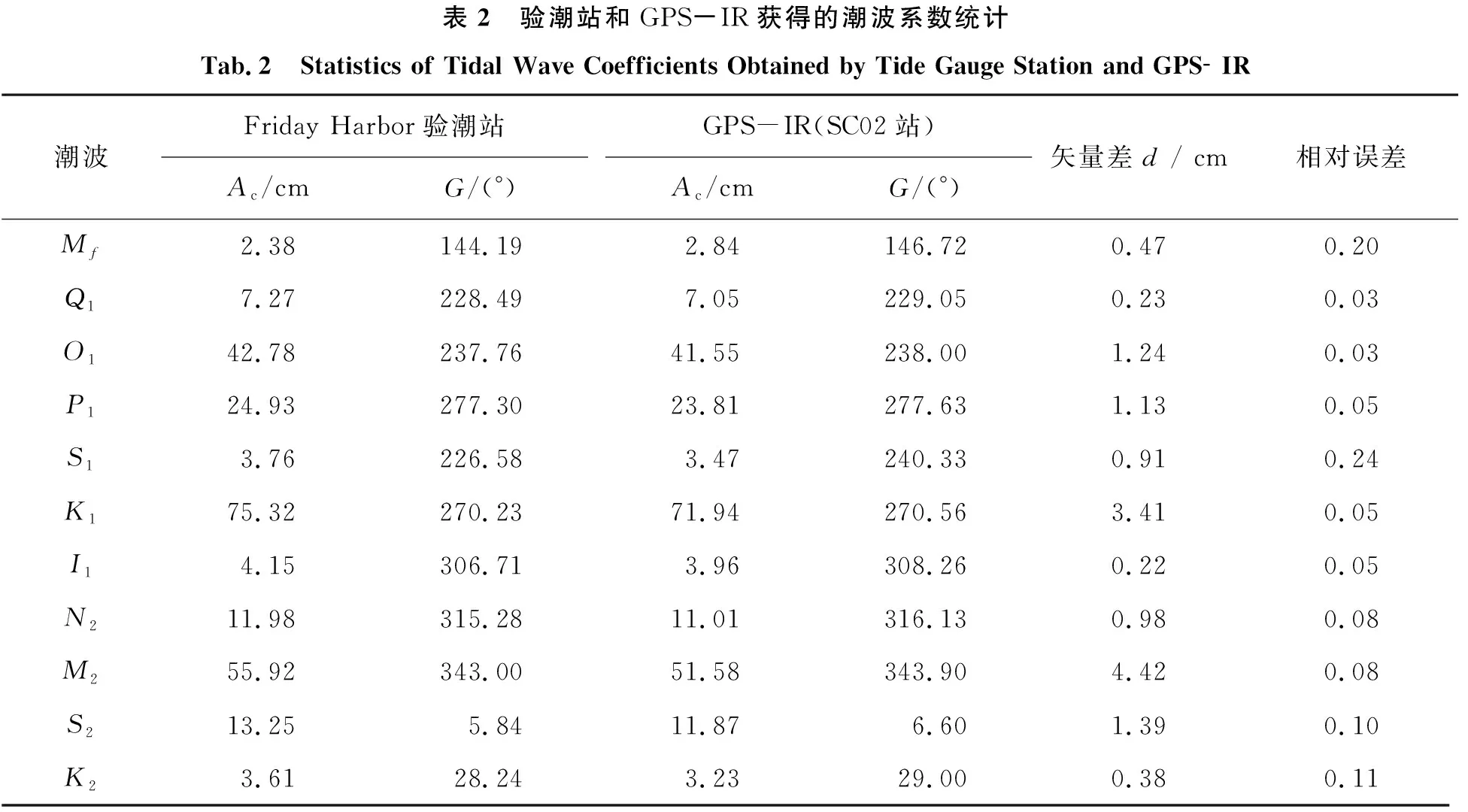
表2 验潮站和GPS-IR获得的潮波系数统计Tab.2 Statistics of Tidal Wave Coefficients Obtained by Tide Gauge Station and GPS IR潮波Friday Harbor验潮站Ac/cmG/(°)GPS-IR(SC02站)Ac/cmG/(°)矢量差d / cm相对误差Mf2.38144.192.84146.720.470.20Q17.27228.497.05229.050.230.03O142.78237.7641.55238.001.240.03P124.93277.3023.81277.631.130.05S13.76226.583.47240.330.910.24K175.32270.2371.94270.563.410.05I14.15306.713.96308.260.220.05N211.98315.2811.01316.130.980.08M255.92343.0051.58343.904.420.08S213.255.8411.876.601.390.10K23.6128.243.2329.000.380.11

其中，矢量差的计算公式：

d= |A1e-iG1-A2e-iG2|

(7)

式中：A1、A2分别为GPS-IR和验潮站两种方法获得的同一潮波的振幅，G1、G2分别为各自获得的相位值。

由表2可知，GPS-IR获取的振幅和相位与验潮站获取的振幅和相位吻合较好，二者的矢量差均在5 cm以内。其中，振幅大于20 cm的分潮有K1、M2、O1和P1，其矢量差较大，而幅度较小的潮波Mf、Q1和K2的矢量差较小。

由文献[14]可知，Friday Harbor港每天只有一次高潮和一次低潮，为明显的日潮港，K1分潮为振幅最大分潮，其周期为一个恒星日。值得注意的是，K1分潮的频率与GPS卫星星座的轨道频率基本相同，但由于卫星的几何位置与多路径误差相关联，会导致与GPS反射数据类似的数据之间与几何误差相关联，但事实上是其对GPS-IR获取潮波系数的影响相对较小。

另外，GPS-IR和验潮站两种方法之间的差异还有可能与验潮站和GPS站不并址存在一定关系，这种差异也会包含两个地点之间海潮的差异。而对于潮波分析本身而言，只有多于18.6年的时间系列数据才能提供可靠的估计，但是很多混合模型获得潮波仍具有很大的不确定性[15-17]。从矢量差和相对误差角度，两种方法求得的各分潮的幅度和相位相差并不大。综上所述，基于GPS-IR进行潮波分析可以得出与验潮站相当的结果，而对于受温度影响的潮汐成分，GPS-IR技术可能是更好的解决方法。

为了进一步验证上述结论，本文运用TPXO9、 TPXO6.2和DTU10海潮模型，通过双线性内插法获取的潮波系数进行对比分析。GPS-IR反演潮位、TPXO6.2、TPXO9及DTU10潮汐模型得到的9个分潮的潮波系数如表3所示。

表3 GPS站和3个模型获得的潮波系数统计Tab.3 Statistics of Tidal Wave Coefficients Obtained by GPS Station and Three Models潮波TPXO9Ac/cmG/(°)TPXO6.2Ac/cmG/(°)DTU10Ac/cmG/(°)GPS站(SC02)Ac/cmG/(°)Mf1.59170.974 91.55167.636 01.58170.745 62.84146.72Q142.33271.833 10.01347.623 613.44243.035 77.05229.05O159.91204.285 826.19226.016 757.39203.991 241.55238.00P158.76210.440 20.03357.795 755.84212.973 323.81277.63K184.63237.303 542.93240.407 680.41236.806 571.94270.56N214.53325.924 70.01122.798 412.44321.427 111.01316.13M234.3846.372 492.75235.775 845.63303.119 251.58343.90S228.17234.87727.44261.992 123.49229.844 811.876.60K23.01188.790 50.10160.520 92.51160.520 93.2329.00

由表3可知，对于Mf、K1、N2、M2和K2分潮，DTU10模型相较于TPXO9模型和TPXO6.2模型在振幅上与SC02站计算的振幅吻合度最好，而对于Q1、O1、P1和S2分潮，三者的振幅相当；对于迟角而言，TPXO9模型、TPXO6.2模型和DTU10模型与SC02站解算的迟角效果吻合度不太高，三者的差异较大。其原因首先可能是由于海潮模型之间的资料来源以及解算方法不同，导致计算得到的各分潮振幅与相位不同；其次是沿海差异很大，造成TPXO海潮模型在此海域的适用精度不高。另外，有些海域由于底摩擦等因素的影响，理论值和实际值严重不符合，造成潮汐调和分析的迟角差异较大[18-19]。

图6是GPS-IR与TPXO系列模型和DTU模型的迟角、振幅的对比结果。由图6可以明显地看出，GPS-IR技术反演结果与验潮站观测结果整体吻合较好，因此，相较于TPXO9、TPXO6.2和DTU10模型，GPS-IR技术在反演获取潮波系数方面有着较高的精度。

图6 GPS-IR与TPXO系列模型、DTU模型迟角和振幅对比Fig.6 Contrast of Delay Angle and Amplitude among GPS- IR , TPXO Series Models and DTU Models

3 总结与展望

本文基于SNR观测值的GPS-IR监测潮位变化，结合潮汐学理论，深入研究了获取潮波系数的方法，并与海潮模型进行了对比分析。以沿海水域监测为例进行研究分析，将GPS- IR技术应用于潮位变化实时监测研究中，通过实例分析并证明了GPS- IR技术用于获取潮波系数的精度高于TPXO9、TPXO6.2和DTU10这3种海潮模型获取潮波系数的精度。

GNSS-IR技术在获取区域潮波系数上有着时空分辨率高、运行成本低、不与海水接触、一站多用等优势，同时获取高精度潮波系数为GNSS-IR技术融合卫星测高，服务于渔业、港口建筑和海水动力利用等提供了非常大的可能性[20-21]。值得注意的是，本文没有深入研究多项式拟合去除趋势项的方法和高度角的选取方法，仅是对一个测站进行了试验分析，后续还需通过大量的测站数据进行验证解算，对比不同去除趋势项的方法，并结合FES、DTU和NAO.99等模型进行研究。