关于激光器扫描结果模拟计算的研究

沈华 徐力

摘 要：从激光器原理出发，总结出激光器扫描的相关特性并得出其扫描线方程，进而在空间直角坐标系中建立一些基本形状的空间坐标系数学模型，结合激光器扫描线的旋转平移，并考虑检测误差、反射率因素等激光器的特性影响，求取其对基本形状物体的有效交点，从而模拟计算出激光器2D或3D扫描的点云数据，为后续模拟算法计算结果以及微调参数提供基础性理论数据支撑，从而便于前期可行性论证及中期的详细系统设计。

关键词：激光器扫描;绕轴旋转坐标转换;线与物体的交点;点云数据模拟计算

中图分类号：TP39    文献标志码：A    文章编号：1671-0797（2022）08-0029-06

DOI：10.19514/j.cnki.cn32-1628/tm.2022.08.009

0    引言

激光器3D扫描技术作为目前较成熟的技术被广泛应用于各种工业用途及民用领域[1]，然而在实际选型中通常忽略对激光器扫描结果的模拟环节，以至于在现场达不到所需的检测精度和效果。因此，需要根据激光器的特性建立空间数学模型，从理论上探讨激光器扫描物体的点云数据，从而实现模拟激光器2D或3D扫描的计算。

1    二维激光器原理及其扫描线的数学模型

1.1    二维激光器工作原理简介

一维激光器的发射器发射激光器脉冲波，当遇到被测物体时，根据物体反射率的不同，激光就会以一定能量被返回，此时激光器的接收器收到反馈的能量后，通过检测从发射到接收的时间差可以推导出激光器光心与被测物体的距离[1]，其公式为：

S=                    （1）

式中：S为被测物体与光心的距离;t2-t1为发射和接收激光的时间差;C为光速。

二維及多线激光器在一维激光器的基础上增加了转动光心的机构，使光心能快速移动，在规定时间内完成一定范围的一维扫描，此时可以实现二维扫描的功能。

1.2    二维激光器主要参数

二维激光器的性能参数主要包含测量距离、反射率、分辨率、测量误差、角分辨率、扫描频率等，通常在选型中主要关注角分辨率、扫描频率、测量距离。角分辨率为相邻检测角度的最小变化角度，扫描频率为1 s时间内完成二维全扫描的次数。

1.3    空间坐标系及坐标系间的转换

首先对空间建立空间直角坐标系并定义其绕3个坐标轴旋转的方向角分别为α、β、γ，如图1所示。

在空间直角坐标系中绕轴旋转的坐标转换公式为：

x1y1z1=cos γ  -sin γ   0sin γ      cos γ    0   0            0       1 cos β  0  sin β    0        1      0-sin β    0  cos β·

1        0            00   cos α   -sin α0   sin α    cos αx0y0z0 （2）

旋转前为[x0 y0 z0]T，旋转后为[x1 y1 z1]T。

将系数整理后，可以得到系数矩阵：

不难得出转换矩阵A为可逆阵，且其逆矩阵A-1中的角度分别为-α、-β、-γ，即符合反方向转回的物理规律。

1.4    二维激光器扫描线数学模型

忽略二维激光器发射器和接收器的相对位置，即定义接收位置为光心，实际扫描线会绕X轴、Y轴、Z轴旋转角度。定义3个轴的旋转角度分别为α、β、γ，扫描角为θ，角精度Δθ。以沿X轴扫描为例，光心位置为原点，在空间直角坐标系中相邻扫描线如图2所示。

此时扫描线在扫描面上移动，相邻两根扫描线之间的夹角即角分辨率Δθ，激光器的坐标系相对世界坐标系的3个轴旋转了α、β、γ。以旋转前沿X轴向下扫描为例，激光器坐标系中，当前扫描线经过原点及[-sin θ 0  -cos θ]T，逆旋转、平移后得到[x1 y1 z1]T=A-1[-sin θ 0  -cos θ]T+[x0 y0 z0]T，[x0 y0 z0]为光心在世界坐标系中的坐标，将[x1 y1 z1]T、[x0 y0 z0]T代入空间直线的含参点斜式方程===t，可以得到m，n，p的相对关系，取确定值后，可以得到扫描线的参数方程：

x=mt+x0，y=nt+y0，z=pt+z0                      （4）

式中：m，n，p为与α、β、γ、θ相关的常数;由于扫描线为射线，t有取值范围（取决于扫描方向）。

如求下一个扫描线的参数方程，其扫描角度为θ+Δθ。

1.5    二维激光器的误差

激光器在二维扫描时可能出现误差，其主要原因是光心旋转中的角度偏差及检测误差。模拟旋转过程中可能出现的角度偏差的方法是在当前扫描角度中增加一个随机误差，其表达式为θ+εθ，其中εθ为随机扫描角度偏差，可根据激光器的特性定义。模拟检测误差则可以在扫描到的理论结果上增加一个扫描线的随机位移量，记作εs。

1.6    二维激光器的反射率

通常，由于激光器功率的限制，反射率会受到一定的影响，当反射率很低且光心到物体的距离较长时，激光器的发射能量会被物体表面吸收导致无法返回。在模拟时需要根据反射率推算其最大的扫描距离从而对结果加以修正，如超过阈值，则扫描线与物体的交点不能被正确读到。

2    激光器三维扫描的数学模型

2.1    激光器三维扫描的方法

激光器的3D扫描是借助激光器作为检测元件。其三维扫描方法有：（1）使用云台，即激光器可以绕轴旋转，以获得被测物体的三维点云数据;（2）使用平移机构带动激光器进行扫描，也可以获得被测物体的三维点云数据;（3）使用多线激光器也可以获得被测物体的粗略三维点云数据[2]。

2.2    旋转光心扫描

如图3所示，激光器光心沿与X轴平行的方向扫描，同时转动轴绕X轴旋转，这样就可以取得被测物体的三维轮廓[2]。在这种扫描方法下，转动轴的角分辨率与激光器的扫描频率有关，忽略光速导致的偏差后，其对应关系为：

δ=                           （5）

式中：δ为转动机构等效角精度;ω为转动机构转动的瞬时角速度;f为激光器的扫描频率。

光心绕轴旋转时，光心相对轴心在X、Y、Z轴方向均有偏差，在转动时需要首先确定光心的位置，可以利用公式（2）相应的旋转坐标系求出当前的光心位置，再利用1.4的内容得到当前时刻的扫描线方程。值得注意的是，多线激光器与旋转光心的数学模型类似，此时光心与旋转中心偏差很小，有时可以忽略。

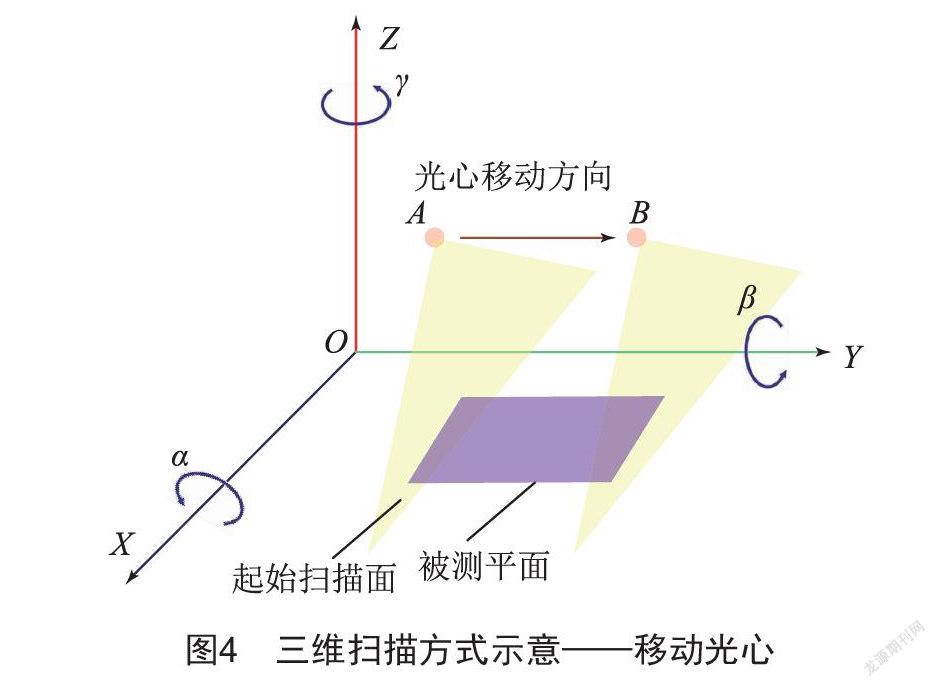
2.3    移动光心扫描

如图4所示，激光器沿与X轴平行的方向扫描，将光心沿与Y轴平行的方向移动，即从A点移动到B点，此时也可以实现下方物体的三维扫描[2]。

考虑加速度的情况下，当前光心位置和前一时刻的位移量与激光器的扫描频率有关，其对应关系可线性近似如下：

ΔS=+                             （6）

式中：ΔS为位移量;V0为前一时刻的瞬时速度;f为激光器扫描频率;a为加速度。

当光心存在多个方向的移动时，需将速度及加速度分解到空间直角坐标系的3个坐标轴进行计算。

3    激光器扫描线与常用空间图形的交点计算

在1.4节中已经求得了当前二维激光器扫描线的参数方程x=mt+x0，y=nt+y0，z=pt+z0， 那么扫描线与空间图形的交点问题实际上就转换为求t值。

3.1    激光器扫描线与平面的交点

平面在空间直角坐标系中的方程为Bx+Cy+Dz+

E=0，已知平面上3个点（其中取2个是最远的顶点以便确定平面上的点的取值范围）[x1 y1 z1]，[x2 y2 z2]，[x3 y3 z3]，代入后可求得系数：

B=y1（z2-z3）+y2（z3-z1）+y3（z1-z2），C=z1（x2-x3）+z2（x3-x1）+z3（x1-x2），D=x1（y2-y3）+x2（y3-y1）+x3（y1-y2），E=-x1（y2z3-y3z2）-x2（y3z1-y1z3）-x3（y1z2-y2z1）      （7）

进而将含参直线方程（如果有旋转的情况可通过公式（2）将直线方程修正为平面的坐标系的方程）代入平面方程中，可以求得t值（需注意直线与矩形平行，即下式中分母为0，t无解）：

t=-                  （8）

注意，点[x0 y0 z0]为光心，需将[x0 y0 z0]根据公式（2）旋转再平移后修正为平面几何中心的坐标。

3.2    激光器扫描线与矩形多面体的交点

将矩形多面体分解为多个矩形进行分析，首先将扫描线折算到平面所在的坐标系，根据3.1的内容求取扫描线与平面的交点，根据矩形的顶点坐标确定在矩形范围内的交点为有效交点，最后将该点旋转平移回世界坐标系。

取矩形多面体上所有交点中与激光器光心的距离最短点，即为当前扫描线与该矩形多面体的交点。

3.3    二维激光器扫描线与菱形多面体的交点

将菱形多面体分解为多个菱形进行分析，取菱形的三点，按照3.1节与平面交点的求取方法求得菱形平面上的交点，此时，假定菱形的两个对角线为X轴和Y轴，长度分别为a、b。将直线方程利用公式（2）旋转到菱形平面并平移坐标转换到菱心，交点[x y 0]需满足公式|ay|+|bx|≤。

同样将所求得的[x y 0]经过旋转平移到世界坐标系，即可求得激光器扫描线与菱形的交点，进而每个面均计算一下交点，取与光心最近的点，即为二维激光器与菱形多面體的交点。

3.4    激光器扫描线与椭球形的交点

在空间直角坐标系中，椭球形的表面空间方程为：

（9）

式中：[x0 y0 z0]为椭球形球心坐标;G、H、J分别为沿X轴、Y轴的赤道半径及极半径。

当G=H=J，则该空间图形为球形。在椭球形表达式中可以以球心为坐标原点，将扫描线的直线方程旋转平移到椭球形的参考坐标系，再将经过旋转平移的公式（4）代入椭球形的方程求得t，此时大多数情况下会有2个t，取与光心最近的点即为扫描线与椭球形的交点。

3.5    激光器扫描线与圆管的交点

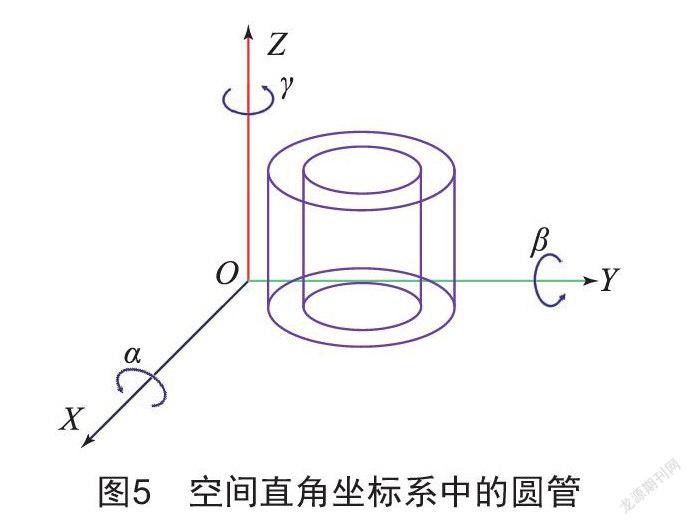
在建立圆管的模型前，首先使得圆管的圆面平行于XOY面，长度方向为Z轴方向，如图5所示。

定义圆管的几何中心为[x1 y1 z1]，外径为R1，内径为R2，高度为H，当内径R2=0时，这个图形为圆柱。将圆管分解为上下顶面及侧面。

激光器与上下顶面的交点求法为：将激光器扫描线坐标系旋转到圆管坐标系，根据3.1的方法求取到上下顶面的交点，并取满足公式R22≤（x-x1）2+（y-y1）2≤R12的点。

圆管外侧面的点满足公式：

（x-x1）2+（y-y1）2=R12，|z-z1|≤       （10）

圆管内侧面的点满足公式：

（x-x1）2+（y-y1）2=R22，|z-z1|≤              （11）

将公式（4）代入求得t值，将坐标系旋转平移到世界坐标系，注意对于圆管，扫描线可能与其有4个交点，即4个t值，取其中与光心距离最短的点即为圆管与激光器扫描线的交点。

4    激光器扫描的模拟方法

根据前面所述，可以根据激光器的扫描模型求取每根扫描线的交点，再进行扫描面的旋转或者光心的平移，可以通过程序实现激光器线扫或3D扫描的模拟。

图6为激光器扫描的模拟运算流程图。

4.1    常用空间图形的模拟3D扫描结果

模拟扫描长方体结果及其图形如图7所示。

模拟扫描球体结果及其图形如图8所示。

从图中可以看出，激光器3D扫描球形的理论最大是扫到半个球，但与角精度的关系很大。

模拟扫描菱形斜面结果及其图形如图9所示。

模拟扫描圆管结果及其图形如图10所示。

4.2    多图形混合的模拟结果点云图形

结合圆管、长方体、斜面、球形等空间图形，可以初步模拟各类基本的物体，利用对应的空间关系模拟出引导车（实例参数如下：角精度0.25°，云台转动速度10（°）/s，激光器采样频率25 Hz，扫描角度0°～180°，光学中心即转动中心坐标，引导车底面中心）的扫描结果及点云图形，如图11所示。

由于目标引导车的边缘值为X方向±1 500 mm，X方向总长应为-7 600～7 400 mm，由结果可以看出，目前3D扫描的X方向理论误差为约4.5 mm，Y方向理论误差为约139.5 mm。

将5 706个计算结果导入Excel表格，得到扫描结果的数据（截取部分数据）如图12所示。

5    结语

模拟激光器扫描结果的方法如下：依据激光器及3D扫描方法（平移或摆动）的特性可以取得其含旋转参数、随机角度及交错模式下的扫描线的数学模型，进而建立空间直角坐标系，将被测物体分解成多个常用空间图形，通过旋转平移矩阵的修正，求取其与扫描线的各个交点后取最近的交点;校验最近的点及物体反射率关系再加入随机偏差，最终求得点云数据。此时，通过数据已经可以得出初步的扫描的误差，并可以为进一步研究算法结果和精度论证提供必要的理论点云数据。由于笔者水平有限，如有问题和错误，请读者谅解并指正。

[参考文献]

[1] 李鑫慧，郭蓬，臧晨，等.激光雷达技术研究现状及其应用[J].汽车电器，2019（5）：4-6.

[2] 王扶.三维激光雷达成像数据处理与可视化研究[D].成都：电子科技大学，2011.

收稿日期：2022-02-28

作者简介：沈华（1984—），男，江苏吴县人，高级工程师，研究方向：机械设备的电气控制、自动化控制、识别及其相關设计。