微分形式动量方程的形成和使用1)
2022-04-28黄树新
黄树新
(上海交通大学工程力学系,上海 200240)
(上海交通大学水动力学教育部重点实验室,上海 200240)
(上海交通大学海洋工程国家重点实验室,上海 200240)
从2019 年春季学期的教学开始,作者使用的课本是丁祖荣老师新修订的《流体力学》第三版[1]。相比第二版[2],这本新修订的书中修改量超过半页纸的内容不低于20 处,如涡动力学方程、人类对机翼升力的认识等。考虑到教材有些变化,作者就对少量新修订的内容做了教学调整[3-4]。在调整教学内容的过程中,作者注意到新版书中提到的微分形式动量方程的历史细节,便查阅了一些资料。这里,介绍一下作者对这个方程的形成和使用的看法。
1 动量方程的历史
在讲Navier–Stokes(NS)方程前,一般是先讲微分形式的动量方程[1,5-7]。然后,再结合Stokes 使用的应力表达式[8],得到NS 方程。所以,微分形式的动量方程是一个基本的方程,它一般写为
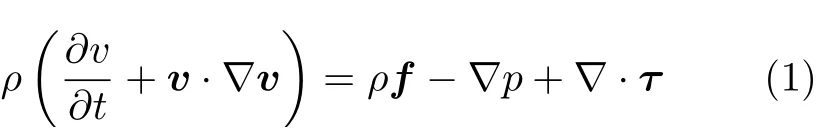
其中,ρ是流体的密度,v是速度矢量,t是时间,∇是梯度算子,f是体积力矢量,p是压强,τ是应力张量。这个方程在书上还常被称为微分形式的运动方程[5],或黏性流体运动一般微分方程[1],或以应力形式表示的黏性流体运动(微分) 方程[7,9],或以应力表示的运动方程[10],或运动方程[11]。
在丁老师最近新修订的《流体力学》第三版中[1],增加了这么一段话,“柯西(A.Cauchy)于1822 年引入了应力张量概念,得到了连续介质运动方程的一般式,但也未解决黏性流体运动的问题”。这个柯西的一般式应该就是式(1)。也就是说,式(1) 还可以称为柯西运动方程。
在作者的印象中,第1 次看到把式(1) 称为柯西运动方程是在读博士期间,当时用的课本是江体乾老师的《工业流变学》[12],书中把式(1)称为柯西应力方程。后来,虽然也阅读了茅春浦老师、孙祥海老师等的课本[9-10],以及上课时用丁老师的《流体力学》第一版[13]和第二版[2],但书中都没有将式(1)和柯西联系起来,也就没再想这个方程怎么称呼,上课时就说这个方程是运动方程。近年来,因看到丁老师在第三版中增加的内容,就查了一下这个方程和柯西的关系。
在文献[12,14-17] 中,均指出式(1) 是柯西给出的方程,而且文献[14,16-17] 均把式(1) 称为柯西运动方程。这样看来,式(1) 是柯西给出的。
在武际可老师的《力学史》[18]的附录中,给出了1920 年以前力学发展史上的100 篇重要文献,其中2.5 节第10 篇文献就是柯西的工作[19],里面有运动方程。查阅柯西1828 年的这篇文章,其中的运动方程为
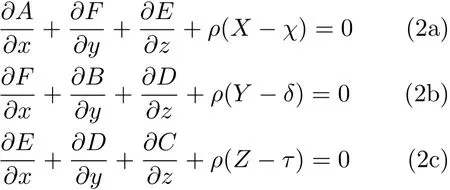
其中,A,B,C是法向应力;D,E,F是剪切应力;x,y,z是空间坐标;X,Y,Z分别是x,y,z三个方向上的重力;χ,δ,τ是加速度。这个τ和式(1) 中的τ是同一个希腊字符,但柯西的原文中就是用这个字符,所以这儿没有改变这个字符。这个式子和式(1)是一致的,区别是形式上还没有把压强项独立出来。
Stokes[8]在1845 年的工作中使用的以应力表示的运动方程是

其中,P1是法向应力,T2和T3是剪切应力,u是x方向的速度,t是时间。这个方程是x方向的运动方程,和式(2a) 对应。因此,Stokes 给出动量方程的时间比柯西晚。
2 动量方程的使用
Stokes 从式(3) 出发还给出了流体力学中的基本方程,即常说的NS 方程。流体力学主要是研究水和空气的宏观运动的学科,因此NS 方程在航空、航海、环境以及工业等领域有着广泛的用途。所以,式(1) 在流体力学上的使用和Stokes 这个人有关,式(1) 或许还可以称为斯托克斯运动方程。
随着科技的发展,以高分子材料的合成、加工和应用为代表的工业中,出现了大量高分子流体。这类黏弹性流体的流动一般不能用NS 方程进行描述,对其研究的出发点就是采用式(1)表达的运动方程,同时,还要结合描述这类流体力学性质的本构方程[12,20]。因此,式(1)表达的运动方程,适用更多的流体流动问题。
第一次用运动方程结合流体的本构方程研究黏弹性流体流动的工作,是Rivlin[21]在1948 年发表的一个工作。这比Stokes 在1845 年用运动方程解决黏性流体的流动问题晚100 年。Rivlin 在这份工作中使用了一个现在被称为Reiner–Rivlin 方程[12]的流体模型,这个模型为
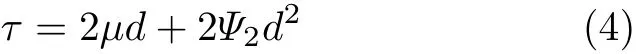
其中,d为形变速率张量,µ为流体的黏度,Ψ2是第2 法向应力差系数。Rivlin[21]在第15 和16 两个小节分别求解了角速度不变的圆柱状流体的旋转流动和角速度变化的无限长同轴圆筒间的流动。
近3 年,在课上讲完NS 方程及其应用后,作者又提了一下运动方程(1)。说这个式子,还适用于描述既有黏性又有弹性的流体的流动,以表示这个式子的重要性。
3 结语
本文介绍了流体力学中运动方程的形成和使用情况。文献表明,微分形式的运动方程是由斯托克斯第一次正确地用于实际流体的流动问题[8]。式(1)用途广泛。
致谢
感谢中国高等教育数字图书馆上海市文献信息服务中心和上海交通大学图书馆提供了Cauchy 和Stokes 的文献。
