新型轻钢复合墙体承重抗火试验及其墙柱热翼缘温升简化计算研究

2022-04-28叶继红

建筑科学与工程学报 2022年2期

陈伟，刘琨，叶继红，姜健，高亮，刘彬

(1. 中国矿业大学江苏省土木工程环境灾变与结构可靠性重点实验室，江苏徐州 221116；2. 中国矿业大学徐州市工程结构火安全重点实验室，江苏徐州 221116；3. 浙江建筑职业技术学院建筑工程学院,浙江杭州 311231)

0 引言

轻钢复合墙体一般是以壁厚1～2 mm的C型冷成型钢龙骨通过自攻螺钉连接组成墙体骨架，而后在骨架两侧通过自攻螺钉连接覆盖建筑板材及保温材料形成的墙体结构[1-3]。当前，石膏板和玻特板是该类复合墙体的常用板材，岩棉和玻璃棉则是常用的保温材料。轻钢复合墙体是低多层轻钢房屋建筑结构体系的主要承重以及抗侧部件，其耐火性能是设计该类结构体系的关键。

已有的轻钢复合墙体抗火试验研究表明：将保温层设置于墙体空腔内部会对该类承重复合墙体的耐火性能产生不利影响[4-6]；将保温层置于墙体空腔外侧有利于墙体耐火性能提升[7-8]。此外，常见同侧双层石膏板和玻特板覆板轻钢承重复合墙体的耐火极限一般在40～90 min区间[4-7,9-11]，远不能达到中国《建筑设计防火规范》规定的一级耐火等级的承重墙耐火极限(180 min)要求。因此，有必要发展一类具备高耐火极限的轻钢承重复合墙体构造形式。

中国现行《建筑钢结构防火技术规范》规定了钢构件耐火极限的2类设计方法，即承载力法和临界温度法。临界温度法的计算思路为：已知钢构件的荷载水平，通过规范查表，确定钢构件的受火失效临界温度，进而根据钢构件受火升温的简化表达式，确定钢构件达到相应临界温度的受火时间，即为该构件耐火极限。临界温度法计算简便，便于工程设计使用，钢构件受火升温简化表达式是临界温度法的应用关键。对此，《建筑钢结构防火技术规范》给出了受火均匀温度分布的钢构件升温简化表达式。然而，已有研究表明，火灾环境下轻钢复合墙体的钢龙骨横截面存在明显的温度梯度[4-13]。因此，已有规范的钢构件升温简化表达式对于该类复合墙体并不适用。同时，已有的轻钢复合墙体受火瞬态传热简化模型[14-15]存在计算繁琐和工程设计使用不便的问题。

本文借鉴了蒸压加气混凝土(ALC)板优异的保温隔热性能[8]，开展以ALC板和玻特(CS)板作为覆面墙板的空腔无填充轻钢承重复合墙体抗火试验，并完善该类复合墙体的龙骨热翼缘受火温升简化计算方法，为轻钢复合墙体的耐火极限高效求解提供基础。

1 轻钢复合墙体足尺模型抗火试验

1.1 试件设计

本文设计制作了1片足尺(3 m×3 m)ALC板-玻特板覆面轻钢承重复合墙体试件S1，其横截面构造如图1所示。试件采用G550(名义屈服强度为550 MPa)C89型(龙骨截面尺寸为89 mm×40 mm×13 mm×1.0 mm)冷成型钢龙骨拼装组成墙体骨架(图2)；骨架两侧采用50 mm厚ALC板作为外保温及面层覆板，采用12 mm厚玻特板作为基层覆板。为了提高墙体的抗剪性能，克服基层墙板拼缝敞开对墙体抗火的不利影响[16]，在龙骨骨架的受火侧两层覆板之间添加0.5 mm厚钢蒙皮，在龙骨骨架背火侧基层玻特板拼缝处添加0.5 mm厚、100 mm宽钢带。

图1 轻钢复合墙体试件横截面构造Fig.1 Cross Section Structure of Light Steel Composite Wall Specimen

图2 足尺试件典型施工过程Fig.2 Typical Construction Process of Full-scale Specimen

1.2 试验设备与制度

本文试验设备采用中国矿业大学大型垂直试验炉抗火试验系统(图3)。试件S1采用承重抗火试验制度，竖向荷载为每柱15 kN，对应荷载比率为0.27[4](试件竖向荷载与其室温竖向承载力的比值)；试验试件单面受火，火灾环境为ISO 834标准火灾温升曲线。图3为试验准备就绪后状态，将模型加载至指定荷载，保持荷载不变且15 min后开启试验火炉，按规定火灾温升曲线升温，直至模型丧失隔热性、完整性或承载力，达到耐火极限后停止试验。试验过程中，沿试件高度及横截面布置拉线式位移计和热电偶，以监测模型在受火过程中的变形与温度发展。限于篇幅，详细试验制度见文献[4]。

图3 墙体试件承重抗火试验系统Fig.3 Load-bearing Fire Resistance Test System of Wall Specimen

1.3 试验结果

试验过程中，试件S1未丧失隔热性和完整性，表现为高温承载力失效，相应耐火极限为197 min。试验结束后观察发现，受火侧面层ALC板竖向及水平向拼缝出现不同程度敞开(图4)，钢蒙皮表面存在明显的局部屈曲，受火侧基层玻特板整体较完整，试件背火面覆板基本保持原样。此外，试件S1的立柱腹板沿立柱长度方向存在明显的局部屈曲半波，并在距龙骨立柱底部1.0～1.3 m高度范围内出现全截面局部压屈破坏。

图4 试件S1受火后试验现象Fig.4 Post-fire Test Phenomenon of Specimen S1

图5给出试件破坏位置附近的横截面温升及变形曲线。其中，ISO 834代表ISO 834标准温升曲线；FT代表炉内平均温度；FS代表模型受火侧平均温度；HF和CF分别代表龙骨立柱热、冷翼缘平均温度；B1-B2和B3-B4代表两层墙板之间的接触面温度；B2-Cav和Cav-B3代表空腔表面温度；Amb代表模型背火侧平均温度。图5(a)中，FT与ISO 834标准升温曲线较接近，表明试验炉可以提供理想的火灾环境。图5(b)给出了试件中部高度处平面外变形曲线，其中正值代表试件发生向炉内的平面外变形。试验过程中，试件平面外变形不明显，说明试件具有良好的受火平面外刚度，因此竖向荷载作用下试件向炉内平面外变形所产生的立柱荷载-位移效应不明显。此外，抗火试验后期，立柱热翼缘温度明显高于其相邻位置冷翼缘，说明试件立柱全截面局部压屈破坏仍是始于其热翼缘局部屈曲。受火197 min时，试件丧失高温承载力，对应立柱的热翼缘临界温度为464 ℃。

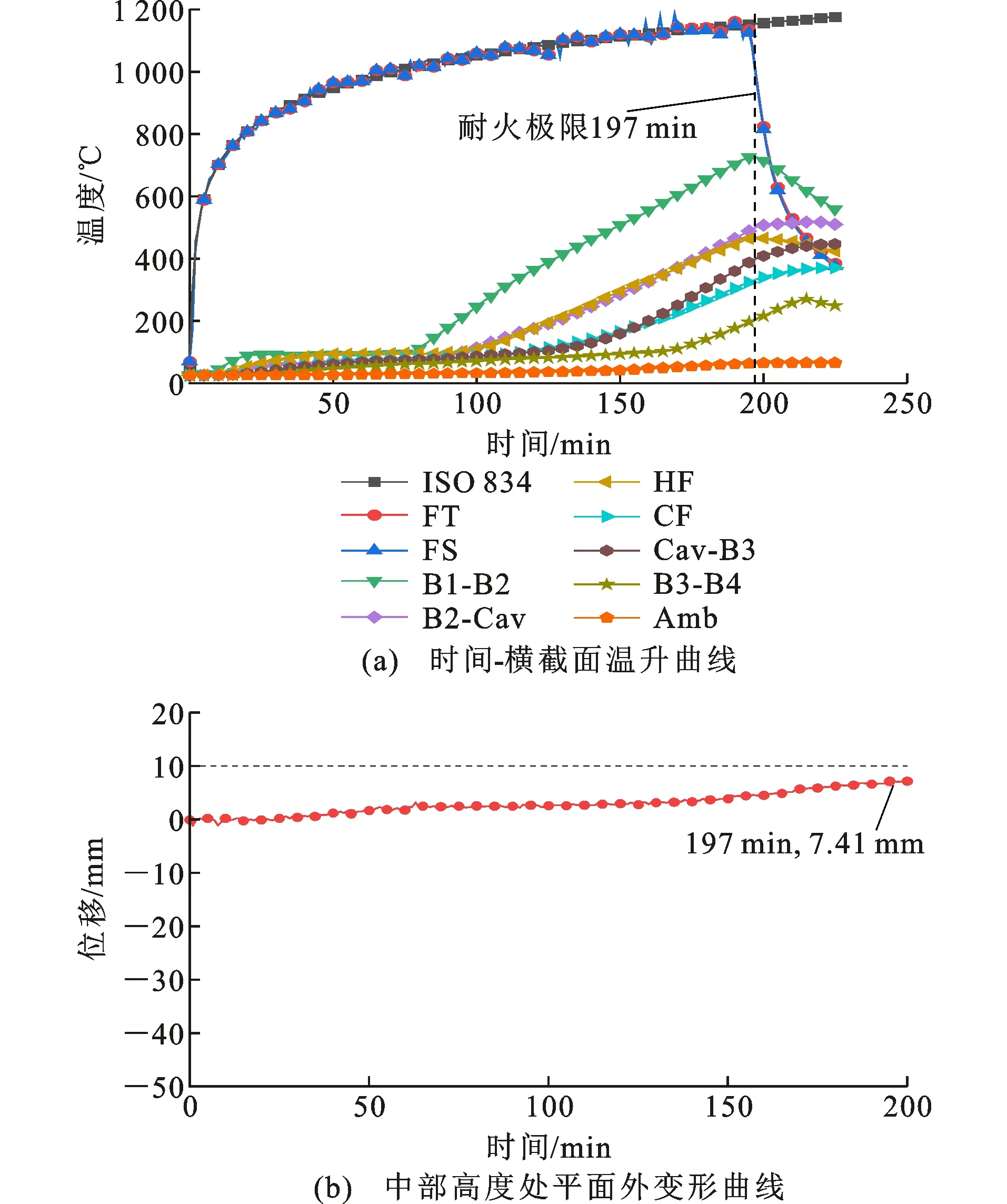
图5 试件S1的温升及变形曲线Fig.5 Temperature Rise and Deformation Curves of Specimen S1

2 复合墙体龙骨热翼缘受火温升简化增量表达式

本文试验以及已有试验研究表明[4-7,9-11]，轻钢复合墙体的高温承载力丧失一般始于龙骨立柱热翼缘局部屈曲。本节基于有限差分方法，推导ALC板-玻特板覆面轻钢复合墙体的钢龙骨热翼缘受火温升简化增量表达式。

2.1 受火传热模型描述

将轻钢复合墙体的受火传热问题等效为一维有限差分传热模型(图6)，且服从如下基本假定：

图6 轻钢复合墙体单侧受火一维有限差分传热模型Fig.6 One Dimensional Finite Difference Heat Transfer Model of Light Steel Composite Wall in Unilateral Fire

(1)将墙体受火侧由不同墙板组成的防火构造措施简化为一层均质防护层，且均质防护层的等效厚度、密度及比热容取为常量。

(2)不考虑墙体沿高度方向上的温度梯度。

(3)忽略龙骨立柱在墙体传热过程中的作用，并偏于保守地假定HF和CF分别与其直接接触的防护层温度一致。

上述3项基本假定中，假定1借鉴了《建筑钢结构防火技术规范》中钢结构防火保护材料等效热阻常量的概念；假定2为建筑结构抗火(小室火)研究的常规假定，一般而言，当建筑室内发生轰燃后，室内空间将处于全面而猛烈燃烧状态，其室内温度一般可近似均匀分布；假定3经前期轻钢复合墙体抗火试验及数值模拟研究证实[9]。

沿均质防护层厚度方向按Δx划分单元(图6)，每个单元的温度与相应节点温度一致，其中，Pm为均质防护层内部节点，Pb1为受火侧均质防护层与火源接触的边界节点，Pb1+1为Pb1节点后下一节点，PHF为受火侧均质防护层与空腔接触的边界节点，即龙骨热翼缘的节点，PCF为龙骨冷翼缘节点，边界节点的单元宽度均为Δx/2，Tf为火源温度，L为墙体宽度，D为空腔深度。

2.2 龙骨热翼缘温升增量公式推导

基于能量守恒原理，图6传热模型的墙体受火侧边界单元Pb1的热平衡方程为

(1)

墙体内部单元Pm热平衡方程为

(2)

墙板空腔边界单元PHF热平衡方程为

(3)

式中：Δt为传热模型的时间步长增量；kE为均质防护层等效导热系数；ρE为均质防护层等效密度；cE为均质防护层等效比热容；dE为均质防护层的等效厚度；εr为固体表面辐射率；σr为Stefan-Boltzmann常量，取5.67×10-8W·(m2·K-4)-1；hf,j为j时刻模型受火侧对流换热系数；hcav,j为j时刻模型空腔表面对流换热系数；Tf,j为火源在j时刻的温度；ΔTb1、ΔTm、ΔTHF分别为节点Pb1、Pm、PHF的温度增量；Tb1,j、Tb1+1,j、THF,j、TCF,j分别为节点Pb1、Pb1+1、PHF、PCF在j时刻的温度；Tm,j为节点Pm在j时刻的温度。

将式(1)、(2)、(3)叠加，可得式(4)。借鉴《建筑钢结构防火技术规范》，对均质防护层热量增量和火源输入热量进行简化，并将空腔热量增量表示为ΔQcav，式(4)改写为式(5)，其中φ为ΔQcav的修正系数，取0.1，时间步长Δt不超过0.5 s。

(4)

(5)

根据ISO 834标准温升曲线，当受火时间t超过120 s且Δt取0.5 s时，ΔTf小于1 ℃。此时，ΔTf的影响可忽略不计。因此，式(5)简化为式(6)。

(6)

2.3 墙体空腔热量增量简化求解

式(7)为墙体模型空腔表面对流换热系数的经验公式[14]。结合式(4)和式(7)可知，当获取不同类型覆板构造的轻钢复合墙体THF与TCF的温差曲线后，ΔQcav可由THF惟一表示。鉴于此，针对ALC板-玻特板覆面轻钢承重复合墙体，采用COMSOL软件计算其THF与TCF的受火平均温差曲线。

hcav,j=2.32(THF,j-TCF,j)0.33(L/D)-0.11

(7)

以试件S1为例，建立其受火传热有限元模型(图7)。数值模型的覆面板材均采用四边形单元，网格尺寸定义为1 mm×5 mm；轻钢龙骨与空腔采用三角形单元，网格尺寸定义为0.5 mm×0.5 mm～5 mm×5 mm。ALC板和玻特板的高温热物理参数试验结果如图8所示[17]，轻钢龙骨的热物理参数取自欧洲规范建议值[18]。模型初始温度取30 ℃，考虑与外界环境的对流及热辐射作用。模型受火侧ALC板外表面温度定义为ISO 834标准升温曲线，ALC板受火侧与火灾环境的对流换热系数取25 W·(m2·K)-1，ALC板背火侧对流换热系数取10 W·(m2·K)-1，模型表面辐射率取0.8。图9为试件S1的受火传热数值模拟结果与试验结果对比，可见数值模型能够合理模拟ALC板-玻特板覆面轻钢龙骨复合墙体受火传热过程。

图7 试件S1的 COMSOL有限元传热模型Fig.7 Finite Element Heat Transfer Model of Specimen S1 Based on COMSOL

图8 玻特板和ALC板的高温热物理参数试验结果Fig.8 Test Results of High-temperature Thermal Physical Parameters of CS Boards and ALC Boards

图9 ALC板-玻特板覆面轻钢复合墙体试验与模拟温升曲线对比Fig.9 Comparison of Temperature Rise Curves Between Test and Simulation of ALC Board-CS Board Sheathed Light Steel Composite Wall

针对ALC板-玻特板覆面轻钢复合墙体，其覆板类型与厚度将直接决定复合墙体的受火传热速度。ALC板常用厚度为37 mm和50 mm，玻特板常用厚度为10～20 mm。选取10种ALC板与玻特板的厚度组合，进行相应复合墙体模型的受火传热模拟，得到龙骨立柱热翼缘与冷翼缘的温差ΔTHF-CF随热翼缘的温度变化曲线，如图10所示。以图10中A37-C10-CFSW模型为例，其编号代表复合墙体的面层采用37 mm厚ALC板，基层采用10 mm厚玻特板组合构成。图10中不同覆板厚度构造的复合墙体ΔTHF-CF曲线之间的差值一般不超过50 ℃。

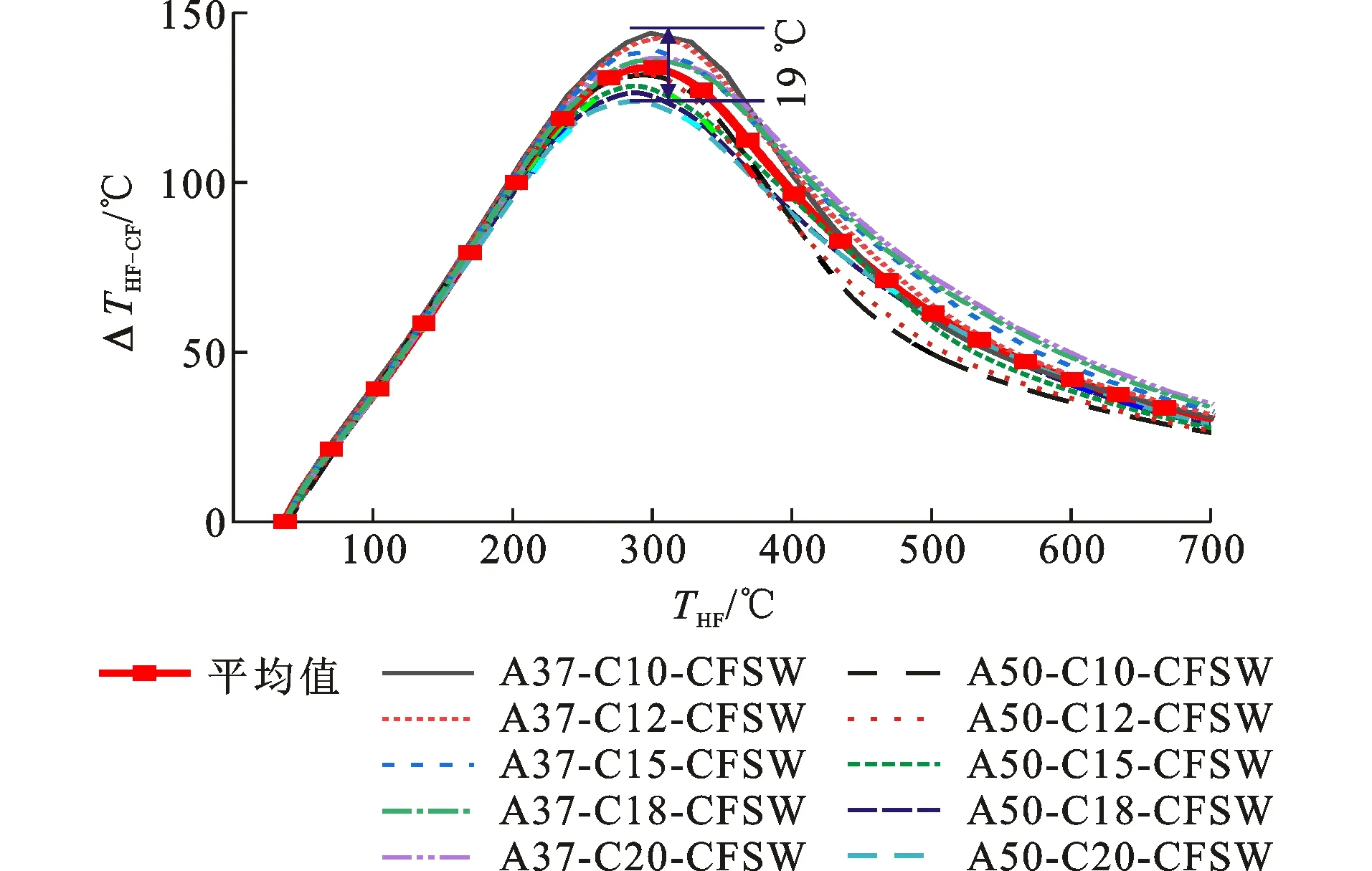
图10 不同厚度组合ALC板-玻特板覆面轻钢复合墙体的热翼缘与冷翼缘温差曲线Fig.10 Temperature Difference Curves Between Hot and Cold Flanges of ALC Board-CS Board Sheathed Light Steel Composite Wall with Different Thickness Combinations

根据图10中THF与TCF平均温差曲线，可得ISO 834火灾环境下复合墙体的Qcav与THF关系曲线，其简化表达见式(8)，系数a、b取值列于表1。因此，ISO 834火灾下ALC板-玻特板覆面轻钢复合墙体的龙骨热翼缘温升增量如式(9)所示。

表1 a和b取值Table 1 Values of a and b

ΔQcav=a+bTHF

(8)

φ(a+bTHF,j)]

(9)

2.4 防护层等效热工参数

为了便于计算，将由ALC板和玻特板组成的简化均质防护层的厚度、密度和比热容加权等效为常量，相应取值见式(10)～(12)，其中ρALC和ρCS分别为ALC板和玻特板的室温密度，取500、1 030 kg·m-3；CALC和CCS分别为ALC板和玻特板的室温比热容，取1 100、1 000 J·(kg·K)-1。

dE=dALC+dCS

(10)

(11)

(12)

以简化均质防护层的dE、ρE和cE为基本参数，将龙骨热翼缘温度达到300～700 ℃作为主控温度区间，即轻钢复合墙体的钢龙骨受火失效温度区间[4-11]。根据主控区间的龙骨热翼缘温升增量公式[式(9)]计算结果与抗火试验或传热模拟结果一致的原则，反向推导防护层的等效导热系数。

式(13)为ALC板-玻特板覆面轻钢复合墙体的简化均质防护层等效导热系数表达式，其中系数a、b、c取值见表2。图11给出ISO 834火灾环境下不同厚度组合的ALC板-玻特板覆面轻钢复合墙体的龙骨热翼缘温升预测结果与有限元模拟结果。可以看出，在钢构件300～700 ℃的温度区间，所提出的龙骨热翼缘温升增量表达式[式(9)～式(13)]预测结果与数值模拟结果吻合良好，其突出优点在于计算过程大幅度简化，便于工程设计使用。

图11 ISO 834火灾下ALC板-波特板覆面轻钢复合墙体THF预测值与有限元模拟值对比Fig.11 Comparison of THF Between Prediction and Simulation Results of ALC Board-CS Board Sheathed Light Steel Composite Wall Under ISO 834 Fire

表2 等效导热系数参数取值Table 2 Values of Equivalent Thermal Conductivity Parameter

kE=a+bdALC+cdCS

(13)

2.5 基于临界温度方法的轻钢复合墙体耐火极限算例求解

如前所述，本文提出的复合墙体钢龙骨热翼缘受火温升简化增量表达式的主要用途是结合临界温度方法确定该类承重复合墙体的耐火极限。对此，学者基于热-力耦合数值模拟结果，给出了双层石膏板覆面轻钢承重复合墙体达到高温承载力耐火极限时荷载比率-龙骨立柱热翼缘临界温度的关系曲线[19]。针对本文涉及的ALC板-玻特板覆面轻钢承重复合墙体，尚需开展大量的热-力耦合数值模拟工作，方可给出相应的临界温度关系曲线。鉴于此，本节仍以试件S1为典型算例，简叙基于龙骨热翼缘临界温度的复合墙体耐火极限求解过程。

(1)根据第1.3节确定试件S1在0.27荷载比率下达到高温承载力耐火极限时所对应的龙骨热翼缘临界温度为464 ℃。

(2)利用式(10)～(13)以及表2确定试件S1中ALC板与玻特板组成的简化均质防护层的等效热工参数为

dE=0.062 m

ρE=602.58 kg·m-3

cE=1 066.91 J·(kg·K)-1

(3)设定试件S1的初始温度为30 ℃，将式(14)～(17)代入式(9)得到其龙骨热翼缘温度达到464 ℃的对应时间为200 min。因此，试件S1的耐火极限预测值为200 min，与试验结果(197 min)吻合良好。