井眼扩径对水平井声波测井响应影响的数值模拟

苏林帅,蔡明,郑占树,徐宝宝,罗居森,胡燕杰,张荆宇

(1.长江大学 油气资源与勘探技术教育部重点实验室, 湖北 武汉 430100;2.长江大学 地球物理与石油资源学院, 湖北 武汉 430100;3.中国石油塔里木油田分公司 安全环保与工程监督中心，新疆 库尔勒 841000;4.中国石油集团测井有限公司 辽河分公司,辽河 盘锦 124011)

0 引言

水平井不但可以降低勘探开发成本，而且还能大幅度提高油气单井产能和采收率。因此，自20世纪末期以来水平井技术在全球范围内得到越来越广泛的应用，国内水平井技术近年来也得到了快速的发展[1]。声波测井是储层评价最重要的手段之一[2-5]，但在水平井中声波测井仪器响应因地层的各向异性、井眼状况、井旁界面、井底岩屑、仪器的偏心状况等影响因素，与垂直井相比表现出极大的差异，进而导致储层声学相关参数评价精度不高，无法满足油田现场勘探开发需求[6]。

为了解决上述声波测井面临的问题，有必要开展(水平井)声波测井正反演研究。国内外学者已开展了大量相关的研究工作。Stephen等[7]将有限差分方法引入井孔声场模拟，并分析了侵入带、井径变情况下的波场，但该方法在固—液界面稳定性差。Randall等[8]使用2.5维的速度—应力有限差分方法模拟了 TI 介质中斜井的声场。Chen[9]用直角坐标系下三维有限差分方法模拟了各向同性介质以及各向异性介质井孔单极源和多级源激发的声场。Mittet和Renlie[10]使用高阶速度—应力有限差分法分析了多极子源下地层各向异性、吸收作用对波场的影响。陶果等[11]采用三维有限差分法对单极和偶极声源激励下的三维声场进行了正演模拟，并模拟计算了井旁含地层界面井孔模型的声场[12]。陈德华等[13]采用优化后的高阶差分法分析井旁裂缝模型下声场的分布。何峰江等[14]使用局部加密交错网格有限差分法研究了贴井壁声波测井仪在裸眼井中的声场。丛健生等[15]模拟计算了水平井孔穿过地层界面时的声速测井响应。陈木银等[16]应用实验的方法研究了在水平井与在垂直井中测量的声波时差的关系，并通过射线追踪法研究了快速夹层影响水平井的声波时差响应临界值图版。杨歆[17]采用二维有限差分正演模拟了水平井存在高速层或岩屑层及仪器偏心时的声波测井响应特征，还研究了不同角度大斜度井中不同各向异性比的地层声波测井时差校正方法。张鹏云[18]对井眼、各向异性等水平井声波测井响应特征的影响因素进行了分析，并提出用岩石物理实验法和统计平移法对水平井声波时差曲线进行校正。Liu等[19]通过模拟水平井和斜井穿透各向异性介质的合成阵列声波数据，研究了井眼倾斜角度、各向异性、井外高速层、井内薄岩屑层等因素对声波传播和实测声波慢度的影响。刘黎等[20]采用三维变网格有限差分模拟研究了裂缝宽度、倾角对井眼声波的传播影响规律，尤其是对横波和斯通利波的衰减影响规律。

上述分析表明，针对水平井声波测井影响因素的研究较少。本文采用三维有限差分方法全面模拟了扩径对水平井声波测井响应的影响，主要考察了径向扩径尺寸、轴向扩径尺寸、扩径位置等因素对水平井声波测井响应的影响规律，特别是对声波时差、到时和幅度的影响规律，研究成果有助于进一步开展水平井声波测井影响因素校正模型与方法研究，进而提高水平井声波测井资料处理解释的精度，更好地为现场生产服务。

1 数值模拟算法的实现与验证

本文采用有限差分方法进行声场数值模拟。在三维直角坐标系下，根据弹性力学的基本假设，假设外力为零，可推导出弹性各向同性介质的速度—应力弹性波动方程：

式中：x、y、z表示空间坐标变量；t表示时间变量；ρ表示密度；λ、μ表示拉梅常数；σxx、σyy、σzz、σxy=σyx、σxz=σzx、σyz=σzy，表示应力分量；vx，vy，vz表示速度分量。

为保证计算精度，上述波动方程离散化时一般采用交错网格[21- 22]。计算模型按交错网格方式剖分，应力、速度分量分布示意如图1。与正应力有关的弹性参数的采样位置和采样时间与正应力一致，与剪切应力有关的弹性参数的采样位置和采样时间与对应的剪切应力分量一致，与速度有关的密度参数的采样位置和采样时间与速度分量一致。

图1 交错网格剖分示意Fig.1 Schematic diagram of staggered grid division

利用二阶差分算子对式(1)的波动方程进行离散化，得到差分方程：

(2)

式(2)中，Dt表示对时间的差分算子；Dx、Dy、Dz表示对空间的差分算子；下标表示空间坐标，上标表示时间节点。

对参数ρ、μ做如下处理：

可以达到自动处理固—液边界的效果，保证了固—液界面上切应力为零。

交错网格有限差分方程属于显式差分时间递推格式的数值算法，即可以按时间节点对速度、应力分量进行迭代计算；在初始时刻(t=0)，速度、应力分量均为零。在三维各向同性介质中，波在各个方向上的稳定性条件是一样的，具体如下：

(4)

其中，vmax是介质中波的最大传播速度;Δx为空间步长;Δt为时间步长;2N为空间阶数;am为系数;m为系数编号。表1给出了常用空间阶数下交错网格差分的系数。

表1 常用空间阶数下交错网格差分的系数Table 1 Staggered grid difference coefficient for common spatial order

根据上述算法开发了相应的三维有限差分声场模拟软件并对图2所示的水平井模型进行了声波测井模拟计算。模型尺寸为2.7 m×2.3 m×2.3 m，井径为0.205 m，介质参数如表2所示，空间步长为 0.005 m，时间步长为0.36 μs，计算时长为4 ms。在模型的边界采用不分裂的卷积完全匹配层吸收波场[23-24]，吸收层厚度为20层空间网格。声源与接收器位于井轴上。单极声源激励信号为主频10 kHz的Rick子波；接收器的最小源距为TR1=1.6 m，间距为0.1 m，共8个接收器。

图2 水平井模型Fig.2 Horizontal well model

表2 地层及井内流体的参数Table 2 Paraments of formation and borehole fluid

图3为源距2.3 m时有限差分法(3D-FD)与实轴积分法(RAI)计算得到的全波波形对比，两者吻合良好，且模式波类型及特征与理论一致；利用STC提取的纵、横波波速分别为3 942.08 m/s、2 267.83 m/s，与模型设置的速度吻合较好，证实了有限差分算法和软件的正确性与可行性。

图3 有限差分(3D-FD)与实轴积分(RAI)波形对比Fig.3 The comparison result of 3D-FD and RAI waveforms

2 井眼扩径对水平井声波测井响应影响的模拟与分析

在地下一定深度的岩层处于受压状态而存在着原地应力，当井眼形成时，井周岩石必然承受原井眼位置岩石承担的部分载荷，结果在井壁周围岩石中产生应力集中现象，若井筒液压支撑不足或岩石强度不够，井壁将破裂形成扩径[25]，进而影响声场传播。本文针对在声源与接收器之间出现不同扩径情况的扩径模型进行了水平井声波测井数值模拟计算。图4为水平井扩径模型示意，井眼是半径为0.1 m的圆柱，扩径部分为以井眼半径为内径的圆筒，均填充井内流体。

图4 水平井扩径模型示意Fig.4 Horizontal well model with borehole expansion

2.1 径向扩径尺寸的影响分析

针对轴向扩径距(扩径圆筒长度)为0.2 m，扩径圆筒厚度(扩径圆筒外内径之差，也称径向扩径尺寸)分别为0.02、0.04、0.06、 …、0.6、0.8、1.0 m，扩径圆筒居中于声源与最近的接收器(R1)之间的水平井扩径模型进行了声波测井数值模拟计算，得到如图5所示的不同模型中2.3 m源距处的接收波形。对各模型中纵、横波幅度及其波速和到时信息进行处理分析，并将纵、横波幅度以无扩径的理想水平井模型的纵、横波幅度为基准做归一化处理，得到归一化幅度、波速和到时随径向扩径尺寸变化关系，分别如图6、图7和图8所示。由图6可以看出，归一化纵、横波幅度均随扩径圆筒厚度的增大而减小，且当扩径圆筒厚度达到或超过0.6 m时归一化幅度受扩径圆筒厚度的影响较小甚至无影响。由图7可以看出，纵、横波的波速始终都接近于地层的波速，扩径圆筒厚度的变化没有对其产生影响，这与理论是相符的(利用阵列波形提取的波速为接收器阵列对应深度段地层的波速)。由图8可以看出，纵波到时随扩径圆筒厚度的增大而增大，且当扩径圆筒厚度达到或超过0.6 m时纵波到时受扩径圆筒厚度的影响较小甚至无影响，说明该模型条件下滑行纵波的径向探测深度约为0.6 m。

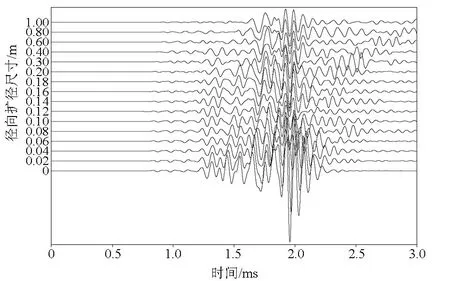
图5 不同径向扩径尺寸条件下的全波波形Fig.5 Acoustic logging waveforms for different borehole radial expansion sizes

图6 纵横波幅度随径向扩径尺寸变化关系Fig.6 The relationship between compressional and shear wave amplitudes with borehole radial expansion size

图7 纵横波速度随径向扩径尺寸变化关系Fig.7 The relationship between compressional and shear wave velocities with borehole radial expansion size

图8 纵波到时随径向扩径尺寸变化关系Fig.8 The relationship between compressional wave arrival with borehole radial expansion size

2.2 轴向扩径尺寸的影响分析

针对扩径圆筒厚度为0.2 m，轴向扩径距(也即扩径圆筒长度)分别为0.1、0.2、0.3、…、1.0m，扩径圆筒居中于声源与最近的接收器(R1)之间的水平井扩径模型进行了声波测井数值模拟计算，得到如图9所示的不同模型中2.3 m源距处的接收波形。对各模型中纵波的幅度和到时信息进行处理分析，并将纵波幅度以理想水平井模型的纵波幅度为基准做归一化处理，得到归一化幅度和到时随轴向扩径尺寸变化关系分别如图10和图11所示。由图10可以看出，归一化纵波幅度随扩径圆筒长度的增大而减小，且在0.4 m附近变化较为平缓，当扩径圆筒长度大于或等于0.9 m时，纵波幅度基本不再随之变化，说明此时滑行纵波基本已在径向上穿透了整个扩径结构。由图11可以看出，纵波到时随扩径圆筒长度的增大而增大，但变化幅度较小。

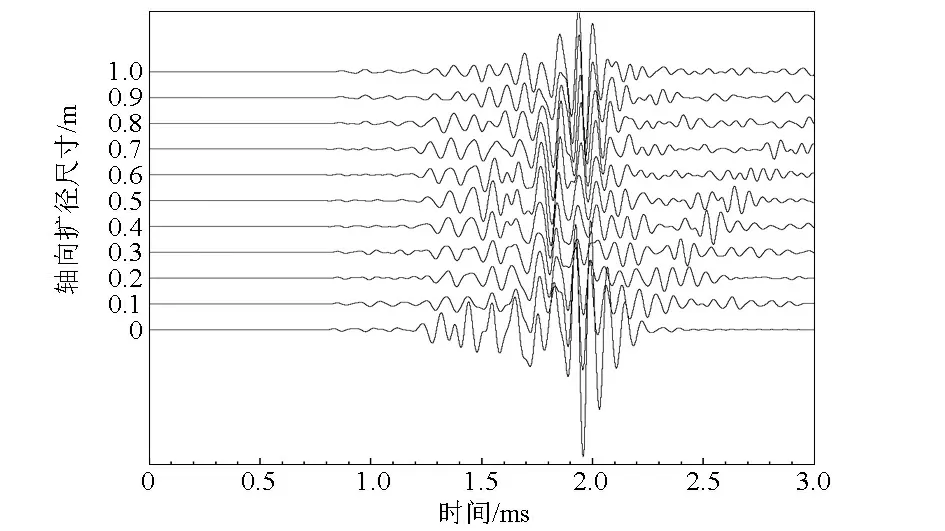
图9 不同轴向扩径尺寸条件下的全波波形Fig.9 Acoustic logging waveforms for different borehole axial expansion sizes

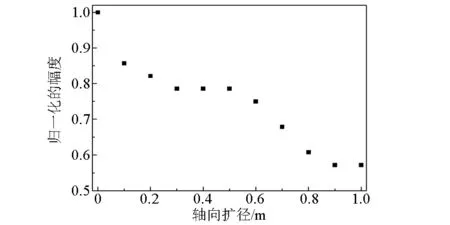
图10 纵波幅度随轴向扩径尺寸变化关系Fig.10 The relationship between compressional wave amplitude with borehole axial expansion size

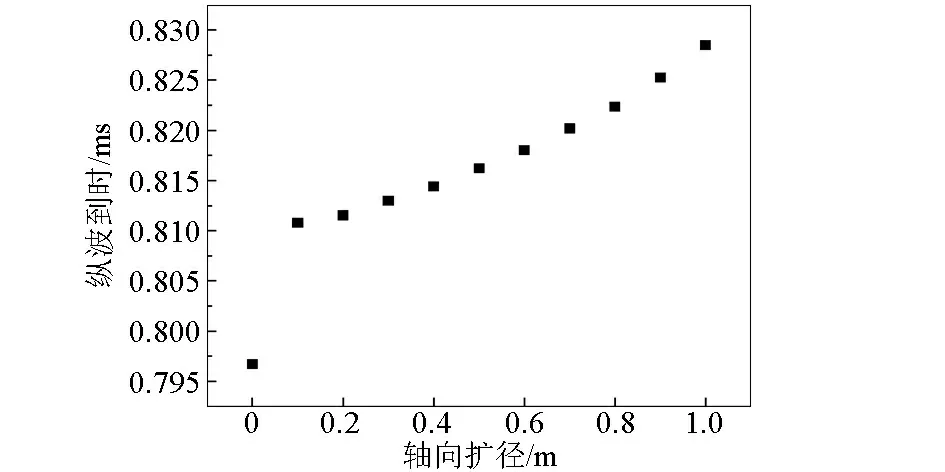
图11 纵波到时随轴向扩径尺寸变化关系Fig.11 The relationship between compressional wave arrival with borehole axial expansion size

2.3 扩径位置的影响分析

针对扩径圆筒长度为0.2 m，扩径圆筒厚度为0.2m，扩径距(声源与扩径圆筒左端之间的距离)分别为0.3、0.4、0.5、 …、1.1 m的水平井扩径模型进行了声波测井数值模拟计算，得到如图12所示的不同模型中2.3 m源距处的接收波形。对各模型中纵、横波的幅度和到时信息进行处理分析，并将纵、横波幅度以理想水平井模型的纵、横波幅度为基准做归一化处理，得到归一化幅度和到时随扩径距变化关系分别如图13和图14所示。由图13可以看出，扩径存在会使纵横波幅度明显降低，但纵、横波幅度基本不受扩径距的影响。由图14可以看出，纵波到时随扩径距的增大而减小，但变化幅度较小，且到0.9 m基本趋于稳定，说明滑行纵波沿轴向传播的同时沿地层径向穿透深度也逐渐增大，且当纵波沿轴向传播约0.9 m时其径向穿透深度约等于或超过该模型径向扩径尺寸，故纵波到时受扩径影响微弱或基本不受影响。

图12 不同扩径距条件下的全波波形Fig.12 Acoustic logging waveforms for different borehole expansion position

图13 纵横波幅度随扩径距变化关系Fig.13 The relationship between compressional and shear wave amplitudes with borehole expansion position

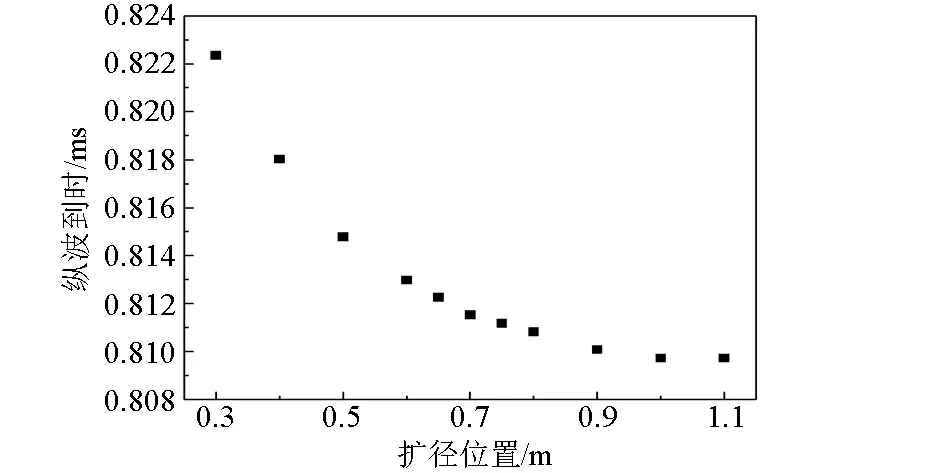
图14 纵波到时随扩径距变化关系Fig.14 The relationship between compressional wave arrival with borehole expansion position

3 结论与展望

针对井眼扩径对水平井声波测井响应影响的问题，本文采用有限差分法开展了正演模拟研究，主要针对径向扩径尺寸变化、轴向扩径尺寸变化和扩径位置变化三大类情况开展了正演模拟计算，并对模拟波形数据进行了处理分析，重点研究了井眼扩径对水平井声波测井波形幅度、到时和波速的影响，取得如下几点认识:

1)当扩径段位于声源与最近的接收器之间时，扩径属性参数变化对纵、横波波速测量结果无影响，但均会导致波形幅度明显降低。

2)径向扩径尺寸变化时，纵、横波幅度均随扩径圆筒厚度的增大而减小，且当扩径圆筒厚度达到或超过0.6 m时幅度受扩径圆筒厚度的影响较小甚至无影响；另外，纵波到时随扩径圆筒厚度的增大而增大，且当扩径圆筒厚度达到或超过0.6 m时纵波到时受扩径圆筒厚度的影响较小甚至无影响。

3)轴向扩径尺寸变化时，纵波幅度随扩径圆筒长度的增大而减小，且在0.4 m附近变化较为平缓；另外，纵波到时随扩径圆筒长度的增大而增大，但变化幅度较小。

4)扩径位置变化时，纵横波幅度基本不受扩径距的影响，纵波到时随扩径距的增大而减小，但变化幅度较小，且到0.9 m基本趋于稳定。

本研究厘清了井眼扩径对水平井声波测井响应的影响规律，可为进一步开展水平井声波测井影响因素校正方法研究提供指导和帮助。本研究未考虑井底岩屑、井顶填充气体等因素的影响，后期可进一步开展相关研究工作。