地—井瞬变电磁三维响应特征分析与异常体快速定位方法研究

赵友超，张军,2，范涛，姚伟华，杨洋,4，孙怀凤,4

(1．山东大学 岩土与结构工程研究中心，山东 济南 250061； 2．山东省交通规划设计院，山东 济南250031； 3．中煤科工集团 西安研究院有限公司，陕西 西安 710077； 4．山东省工业技术研究院 先进勘探与透明城市协同创新中心，山东 济南 250061)

0 引言

瞬变电磁法(TEM)是一种利用电磁感应原理进行勘探的电磁测深方法，通过采集关断间歇产生的纯二次场来分析地下电性分布[1]。瞬变电磁法已被广泛应用于各类勘察工作中，包括矿产资源勘探[2-4]，查找地下水[5-6]以及隧道超前地质预报[7-10]等方面。地—井瞬变电磁法是在常规地面瞬变电磁基础上发展起来的地面发射、井中接收的瞬变电磁勘探方法[11]。相比传统地面瞬变电磁方法，地—井瞬变电磁勘探接收探头置于井下，其接收点更加接近目标体，观测到的响应信号会更强，信号反馈的目标体信息也更加真实可靠；同时也在一定程度上规避了地表电磁干扰[12]。

在地—井瞬变电磁正演方面，中外不少学者都进行过深入研究[13-17]，而在这一领域，地下异常体定位仍是亟待解决的问题。Dyck等[18]采用物理模型试验的方法并结合数值模拟研究了采用地—井瞬变电磁三分量数据对地下目标体进行定位的可行性，提出同时观测三分量数据有助于解决多解性问题，但并没有给出针对异常体定位的确切方法；J.R.Bishop等[19]将地—井瞬变电磁法用于地下磁黄铁矿探查，并取得了良好的应用效果；孟庆鑫等[20]采用时域有限差分研究了均匀半空间以及低阻覆盖层下均匀半空间中的低阻板状异常的响应规律；徐正玉等[21]采用时域有限差分方法研究了均匀半空间模型和垂直断层面模型的地—井瞬变电磁响应规律。目前，对于地—井瞬变电磁异常体定位的正演研究大多处于定性分析阶段，无法明确定位异常体所处范围。

在上述研究的基础上，针对地—井瞬变电磁正演问题的定性分析做了进一步完善。采用时域有限差分方法建立三维模型进行正演计算，研究地—井瞬变电磁响应特征，并在此基础上提出了一种针对井旁异常体的快速定位方法。本研究在孙怀凤等开发的TEM3DFDTD程序基础上完成。

1 地—井瞬变电磁三维正演与规律分析

基于时域有限差分方法，建立三维地电模型进行正演计算[22-23]，分析模型的三分量响应曲线，总结其响应规律，模型如图1所示。采用表1所示模型参数，设异常体为正方体，依据单一变量原则分别改变异常体的电阻率、尺寸、埋深以及水平方位角，对比分析曲线形态特征并总结规律。水平方位角是指异常体中心与坐标原点的连线与X轴正向的夹角。

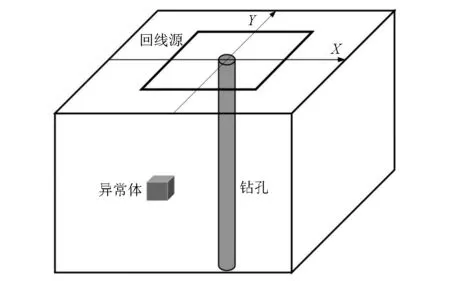
图1 模型示意Fig.1 Schematic diagram of model

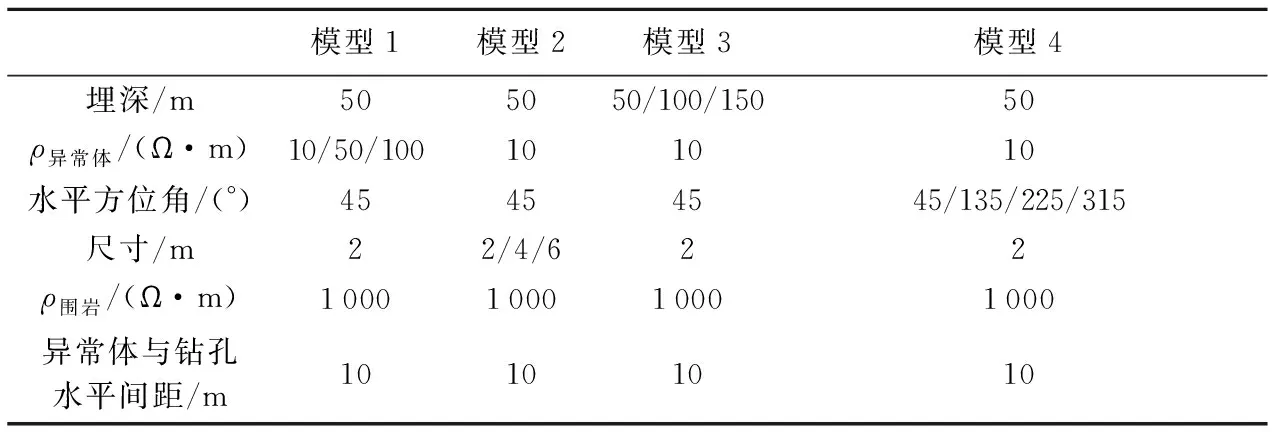
表1 三维模型正演参数Table 1 3-D model forward parameters

为研究异常体电阻率的变化对地—井瞬变电磁三分量响应特征的影响，采用表1中的模型1进行正演计算，结果见图2。分析图2，发现X、Y分量响应曲线零点以及Z分量响应曲线极值点对应的深度即异常体所在深度。此外，随着异常体电阻率的增大，三分量的响应曲线形态均无明显变化，X、Y分量始终呈反“S”型，Z分量保持“V”型。但三分量响应曲线的幅值随异常体电阻率增加而逐渐减小，说明地—井瞬变电磁探测对低阻更为敏感，因此低阻模型的感应电动势响应更强烈。

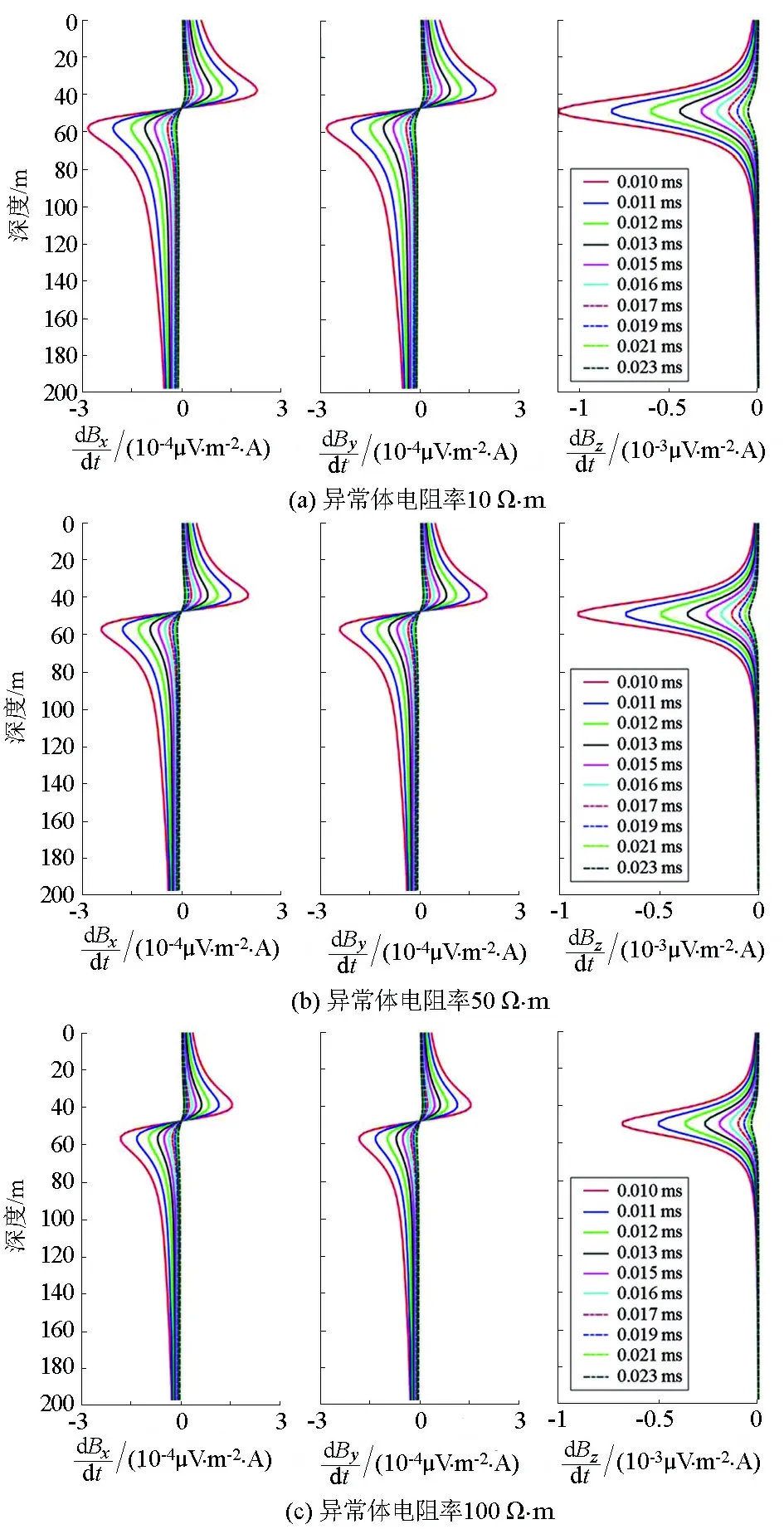
图2 不同电阻率异常体模型的响应曲线Fig.2 Response curves of different target resistivity models

为研究异常体尺寸变化对地—井瞬变电磁响应的影响，采用表1中的模型2进行正演计算。对比分析图3，随着异常体尺寸增加，三分量响应曲线的幅值逐渐增加。当异常体边长为2 m和4 m时，三分量响应曲线形态大致保持不变，仍然可以依据X、Y分量零点以及Z分量极值点定位异常体所在深度。但是当异常体边长为6 m时，X、Y分量曲线在异常体中心附近出现多个零点和极值点，Z分量曲线也在异常体中心附近出现多个极值点，推断该现象是由于异常体距离钻孔太近以及网格尺寸太小等因素引起。

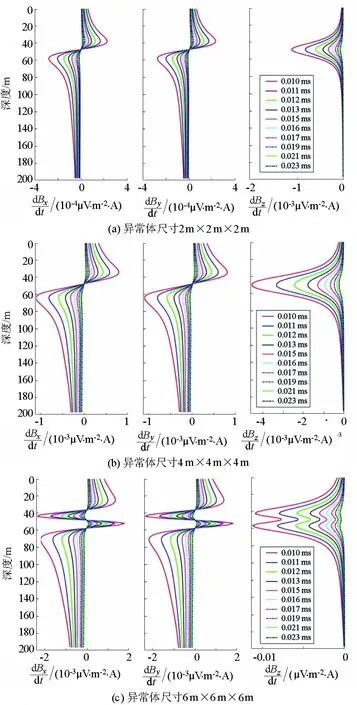
图3 不同规模异常体模型的响应曲线Fig.3 Response curves of different target size

为研究异常体埋深对三分量响应的影响，采用表1中模型3进行正演计算。分析图4发现，随着埋深增加，X、Y分量的曲线形态始终保持不变，且X、Y分量曲线的零点及Z分量曲线的极值点始终对应异常体所在深度。 随着异常体埋深增加，地—井瞬变电磁三分量响应逐渐减弱。

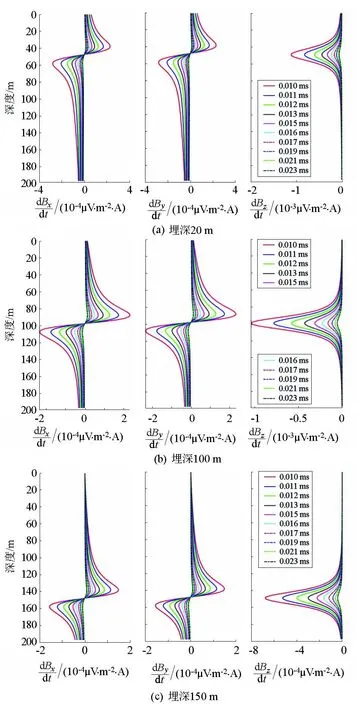
图4 不同目标体埋深模型响应曲线Fig.4 Response curves of different depth of target

为研究异常体水平方位角的变化对三分量响应曲线的影响，采用表1中的模型4进行正演计算。图5显示，当异常体位于不同方位角时，X、Y分量曲线的零点以及Z分量曲线的极值保持不变，均对应异常体中心所在的深度；当异常体位于不同方位时，X、Y分量曲线形态会发生变化。当α=45°时，X、Y分量曲线形态均为反“S”型；当α=135°时，X分量呈“S”型而Y分量呈反“S”型；当α=225°时，X、Y分量均为“S”型；当α=225°时，X分量呈反“S”型而Y分量呈“S”型。

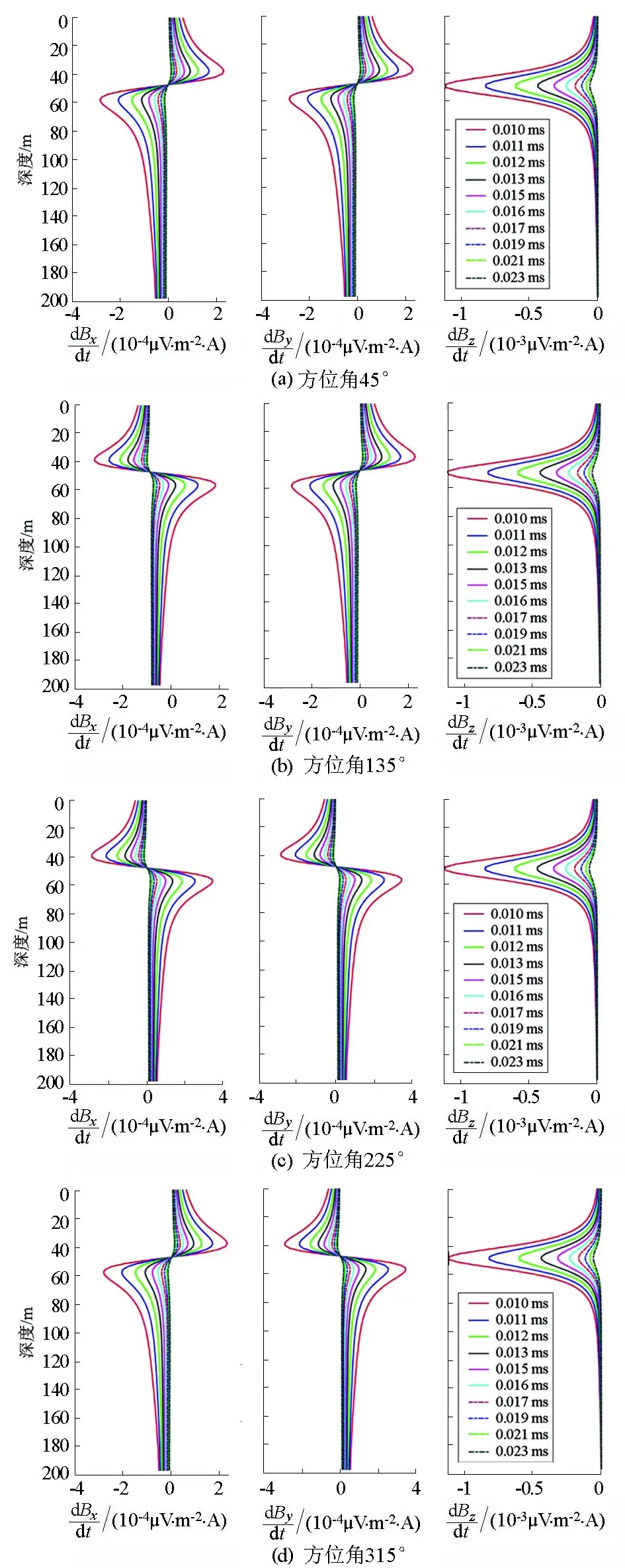
图5 不同水平方位模型的响应曲线Fig.5 Response curves of different target azimuth

综合分析以上研究结果，发现如下规律：纯异常场X、Y分量曲线呈“S”型或者反“S”型，Z分量曲线呈“V”型，X、Y分量曲线的零点以及Z分量的极值点对应异常体所在的深度；由于距离钻孔太近以及网格尺寸太小等因素可能会造成响应曲线在异常体所在深度出现多个极值点；当异常体方位角发生改变时，X、Y分量曲线形态会发生变化，其他参数改变时，X、Y分量曲线形态保持不变。

2 异常体定位方法

在地—井瞬变电磁三维正演计算部分，发现只有当异常体方位发生改变时，X、Y分量曲线的形态才会发生改变。基于数值模拟部分得出的结论，不断改变异常体所在方位，进行大量正演计算，绘制其纯异常响应曲线并进行总结发现如下规律：

1) 当异常体位于第一象限时，X、Y分量曲线形态均为反“S”型；当异常体位于第二象限时，X分量呈“S”型而Y分量呈反“S”型；当异常体位于第三象限时，X、Y分量均为“S”型；当异常体位于第四象限时，X分量呈反“S”型而Y分量呈“S”型。

2) 在同一象限内，异常体位于不同区域时，X、Y分量响应曲线幅值的相对大小有所不同(这里的幅值是指响应曲线极大值点)。如图6所示，将井周360°范围划分成8个区域，不同区域内X、Y分量幅值相对大小如表2所示。

图6 区域划分示意Fig.6 Schematic diagram of regional division

表2 X、Y分量幅值对比Table 2 Comparison of the amplitude of X and Y components

当异常体位于第一、第三象限时，X、Y分量曲线型态一致，可采用X-Y分量来进一步判断异常体所在区域；当异常体位于第二和第四象限时，X、Y分量曲线型态相反，可采用X-(-Y)即X+Y分量来进一步判断异常体所在区域。对上述研究进行归纳总结，提出一种地—井瞬变电磁异常体定位方法，依据该方法可确定异常体所在的深度并将其定位于井周45°范围。该方法对异常体的定位分两步进行：首先依据X、Y分量曲线的零点确定异常体深度；随后，依据X、Y分量曲线形态可以确定异常体所在象限，依据X-Y或者X+Y分量曲线形态可以进一步确定异常体所在的区域，如表3所示。

表3 目标体区域定位Table 3 Regional positioning of target

3 数值算例验证

为了验证提出的地—井瞬变电磁异常体快速定位方法的准确性，选择同一个异常体，设置背景电阻率为1 000 Ω·m，异常体电阻率为10 Ω·m，其所在深度为50 m。改变异常体与X轴正向夹角，依次为30°、60°、120°、150°、210°、240°、300°以及330°，使得目标体分别位于划分好的8个区域并进行正演计算，如图7所示。

图7 异常体方位示意Fig.7 Schematic diagram of target azimuth

图8(图8-1、图8-2)为8个模型的纯异常场分量响应曲线，依据每组模型响应曲线的零点均可确定异常体深度为50 m，与设计模型异常体所在深度相吻合。根据之前提出的水体定位方法，模型1到模型8异常体区域定位结果如图9所示。对比设计模型，发现所有模型定位结果均与异常体所在区域相吻合，数值试验证明了基于总场的地—井瞬变电磁异常体快速定位方法的准确性和可靠性。

图8-1 纯异常分量模型响应曲线Fig.8-1 Pure abnormal response curves of 8 models

图8-2 纯异常分量模型响应曲线Fig.8-2 Pure abnormal response curves of 8 models

图9 异常体定位结果Fig.9 The results of target positioning

4 实测数据验证

为验证提出的异常体快速定位方法的野外适用性，要对其进行现场试验验证。本次现场试验采用的实测数据为文献[24]中的数据，采用本文提出的方法对其进行处理。数据采集所用钻孔位于陕北某矿区，该矿区早期主要采取以掘代采的采煤方法，在地下留下较多的采空区，由于上覆含水层的补给，形成了较多的积水采空区，威胁煤矿生产安全。现已探明位于所选钻孔北偏西15°方向-97 m处存在充水采空区，如图10所示。

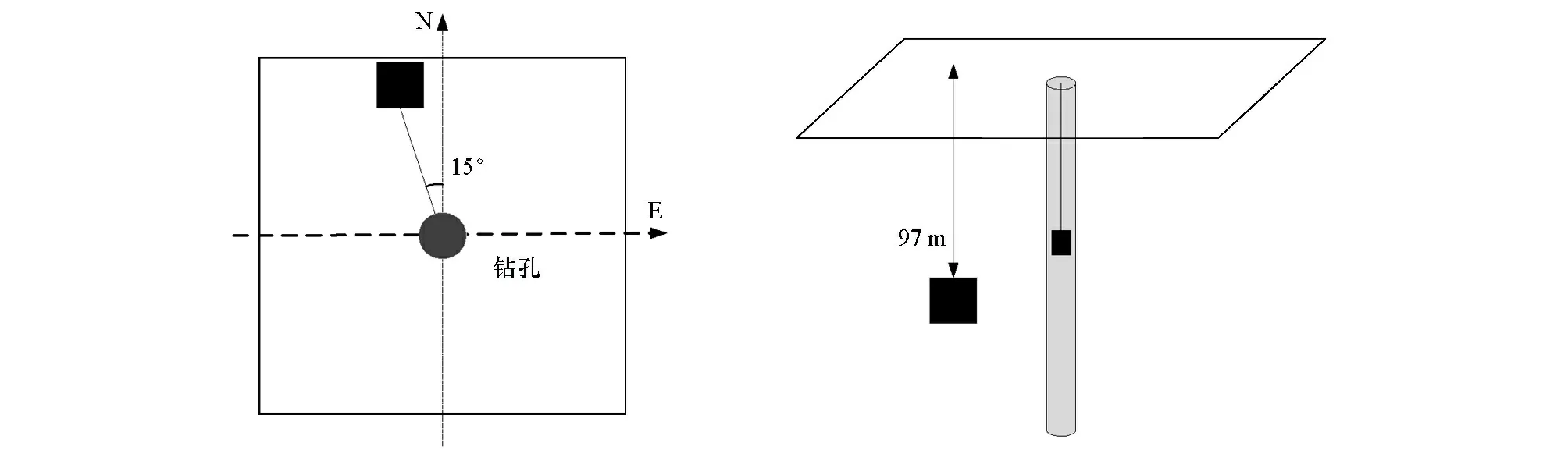
图10 采空区所在区域示意Fig.10 Schematic diagram of the location of the goaf

回线源尺寸设置为360 m×360 m，钻孔位于回线源中间，发射波形为线性关断梯形波，关断时间为0.5 ms，发射电流为20 A。以正东方向为X轴正方向，正北方向为Y方向建立坐标系，采集得到的总场三分量响应曲线如图11所示，提取得到的异常场三分量响应曲线如图12所示。

图11 实测总场三分量响应曲线Fig.11 Total field response curve of measured data

图12 纯异常场响应曲线Fig.12 Pure abnormal field response curve of the measured data

图12为纯异常场的三分量响应曲线，图中红色曲线大致描述了实测数据各分量的曲线形态。X、Y分量曲线的零点以及Z分量曲线的零点所在位置为地下97 m附近，据此可判定积水采空区深度为地下97 m附近。此外，X分量曲线大致呈反“S”型，Y分量曲线大致呈“S”型，因此可判定异常体位于第二象限；X+Y分量曲线大致呈“S”型，因此可进一步判定充水采空区位于第三区域，其定位结果如图13所示，与其实际位置相吻合。

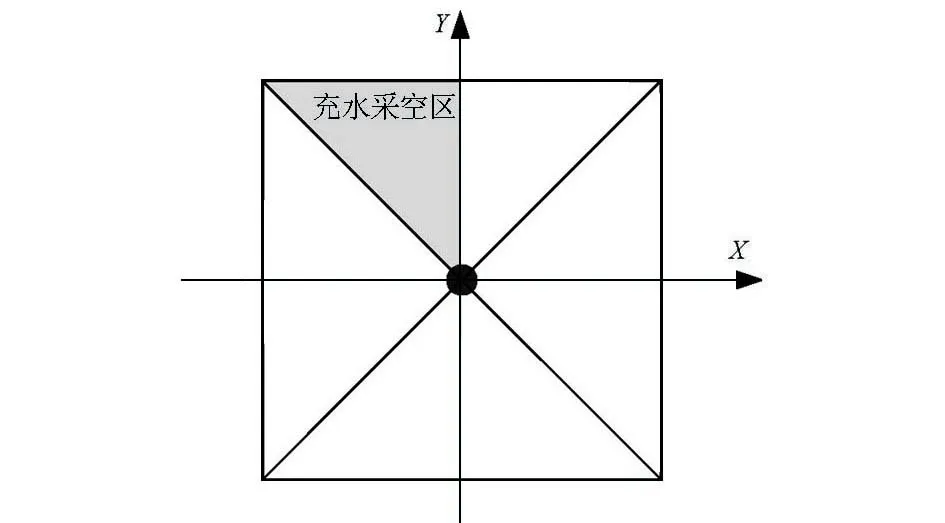
图13 充水采空区定位结果Fig.13 The results of water-filled goaf positioning

5 结论

针对地—井瞬变电磁数据解释以及井旁异常体定位问题，基于时域有限差分方法建立三维模型进行大量正演计算，总结地—井瞬变电磁模型三分量响应规律，在此基础上提出一种井旁异常体快速定位方法。该方法主要依据三分量响应曲线形态以及组合曲线(X-Y或X+Y)形态来确定异常体所在深度并将异常体圈定于井周45°范围，对实际井旁矿体的探测具有指导作用。

地—井瞬变电磁响应特征规律较为复杂，本文提出的方法虽然能够快速圈定井旁异常体，但仍存在一定的局限性且有一定的进步空间。文中仅考虑了含单个异常体的均匀半空间模型的三分量响应规律，而对于背景围岩非均匀以及井旁存在多个异常体等问题仍需进一步深入研究；此外，本文提出的定位方法仅可确定异常体中心深度并将其圈定于井周45°范围，还没有实现异常体的精确定位。下一步工作是进行地—井瞬变电磁反演研究，到达精确定位井旁异常体的需求。