混沌粒子群优化小波神经网络在电能质量扰动信号分类中的应用*
2022-04-28吴炬卓陈书原牛海清陆小鹏
吴炬卓, 陈书原, 牛海清, 陆小鹏
(1.珠海供电局, 广东 珠海 519000;2.华南理工大学 电力学院, 广东 广州 510640)
0 引 言
高新技术的不断发展以及人们生活质量的持续改善,对电能质量提出了更高的要求。与此同时,影响电能质量扰动的因素增多。电网结构的复杂演变,新型电力电子设备的不断应用,清洁能源发电的并网接入等,使得电能质量问题愈发突出[1]。不同的电能质量扰动,其引起原因和治理措施也不同,故准确对电能质量扰动信号进行分类,有利于提高用电体验,减少经济损失,具有重要的价值和意义。
对信号进行分类,特征提取和分类器选取是关键技术所在,其直接决定分类的准确率。特征提取方面,小波变换由于可以很好表征信号的时频域特征,已在电能质量扰动信号的特征提取中得到广泛应用[2-3]。在分类器选取方面,具有非线性映射特点的人工神经网络,已成为电能质量扰动信号分类中的常用方法,且能够取得一定的效果[4-5]。因此,将小波变换和神经网络优势结合,能够有效提高电能质量扰动信号分类准确率。目前,常用的方法为基于小波变换,提取信号的特征向量,并以特征向量为输入,信号类别为输出构建神经网络,对信号进行分类[6-7]。但在信号分类过程中,小波变换和神经网络只是简单组合且互相独立。
为解决此问题,进一步提高信号分类准确率,文献[8]提出一种自适应小波神经网络模型。该模型中,隐含层的传递函数使用小波函数。通过自适应调整小波函数的参数,能够更加有效提取信号时频特征[9-10]。文献[9]和文献[10]分别采用自适应小波神经网络对励磁涌流和局部放电进行分类,分类正确率均为100%。为有效提高电能质量扰动信号分类正确率,本文基于小波神经网络,使用混沌粒子群优化算法对网络进行训练,进而对正常电压和几种常见电能质量扰动信号进行分类。同时分别采用粒子群优化算法和BP优化算法对小波神经网络训练,并比较不同优化算法训练后网络的分类结果。结果表明,混沌粒子群优化小波神经网络能够有效对电能质量扰动信号进行分类,具有受噪声影响小、稳定性好等特点。
1 混沌粒子群优化小波神经网络
1.1 小波变换
假设函数空间为L2(R),存在ψ(x)∈L2(R),且其傅里叶变换ψ(ω)满足容许性条件:

(1)
式中:ψ(x)——母小波函数。
对母小波函数进行伸缩和平移处理,得到小波序列ψa,b(x)。
(2)
式中:a、b——尺度因子、平移因子。
对于f(x)∈L2(R),其关于母小波ψ(x)的小波变换Wf(a,b)为

(3)
1.2 小波神经网络
4层小波神经网络如图1所示。网络包括输入层、小波层、隐含层以及输出层4层,能够对更为复杂的信号进行有效分类,具有更加良好的收敛及泛化性能。
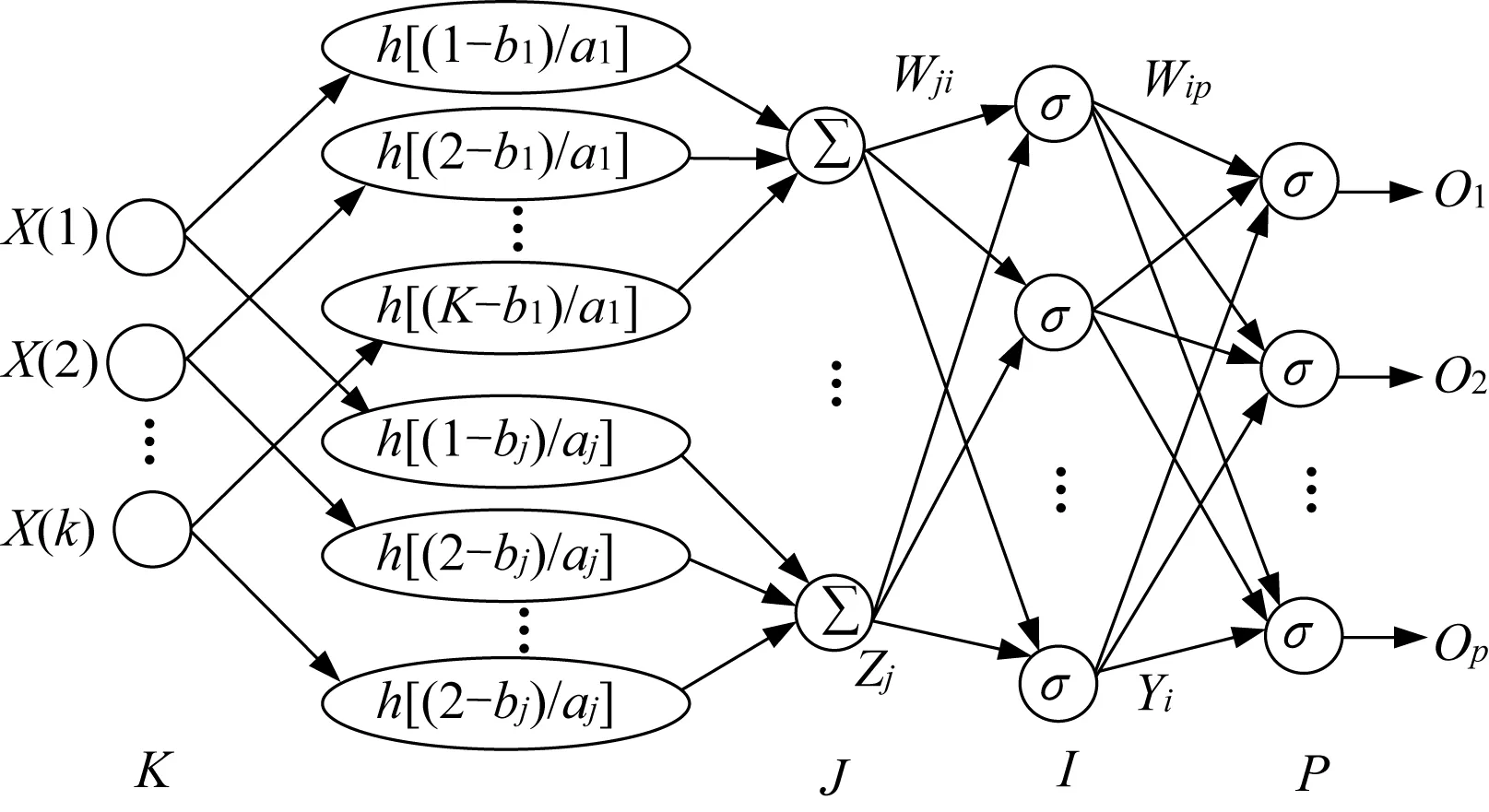
图1 4层小波神经网络
由图1可见,网络由用于信号特征提取的小波层和用于信号分类的前馈神经网络两部分组成。其中,K和x(k)分别为输入层神经元个数和第k个神经元的输入值;J和Zj分别为小波层神经元个数和第j个神经元的输出值;I和Yi分别为隐含层神经元个数和第i个神经元的输出值;P和Op分别为输出层神经元个数和第p个神经元的输出值;Wji为小波层第j个神经元和隐含层第i个神经元的权值;Wip为隐含层第i个神经元和输出层第p个神经元的权值;h(x)为小波层采用的小波函数;aj和bj分别为小波层第j个神经元的尺度因子和位移因子;σ(x)为sigmoid传递函数,则网络的输出值OP为
(4)
1.3 混沌粒子群优化小波神经网络
在小波神经网络结构中,需要对小波函数的尺度因子和位移因子以及层间连接权值进行训练。传统方法是采用BP算法,其实现原理简单,但当网络结构比较复杂和样本数据比较庞大时,网络不易收敛且容易陷入局部最优解,无法得到全局最优解。研究表明,在保证网络收敛至全局最优解方面,群智能优化算法有着良好的效果。
粒子群优化算法[11-12]能够取得比BP算法更好的优化效果,但其在粒子进入早熟时,仍会收敛于局部极值。且在粒子进化后期,算法收敛速度较慢,精度较差。为提高网络训练的速度和精度,本文将混沌引入到粒子群优化算法中,利用混沌运动的遍历性寻找全局最优解。
目前,一般将混沌定义为由确定性方程得到的具有随机性的运动状态,呈现混沌状态的变量则为混沌变量[13-14]。混沌系统中,Logistic方程是其中典型一个,其表达式为
zn+1=μzn(1-zn)
(5)
式中:μ——控制变量;
zn——混沌序列。
μ值确定后,由任意初值z0∈[0,1],通过较长时间的迭代以后,能够得到遍历区间内所有值的混沌系列{zn,n=0,1,2,…}。
基于混沌运动的遍历性,本文将混沌引入到粒子群优化算法中,对小波神经网络进行训练。小波神经网络训练流程如图2所示。
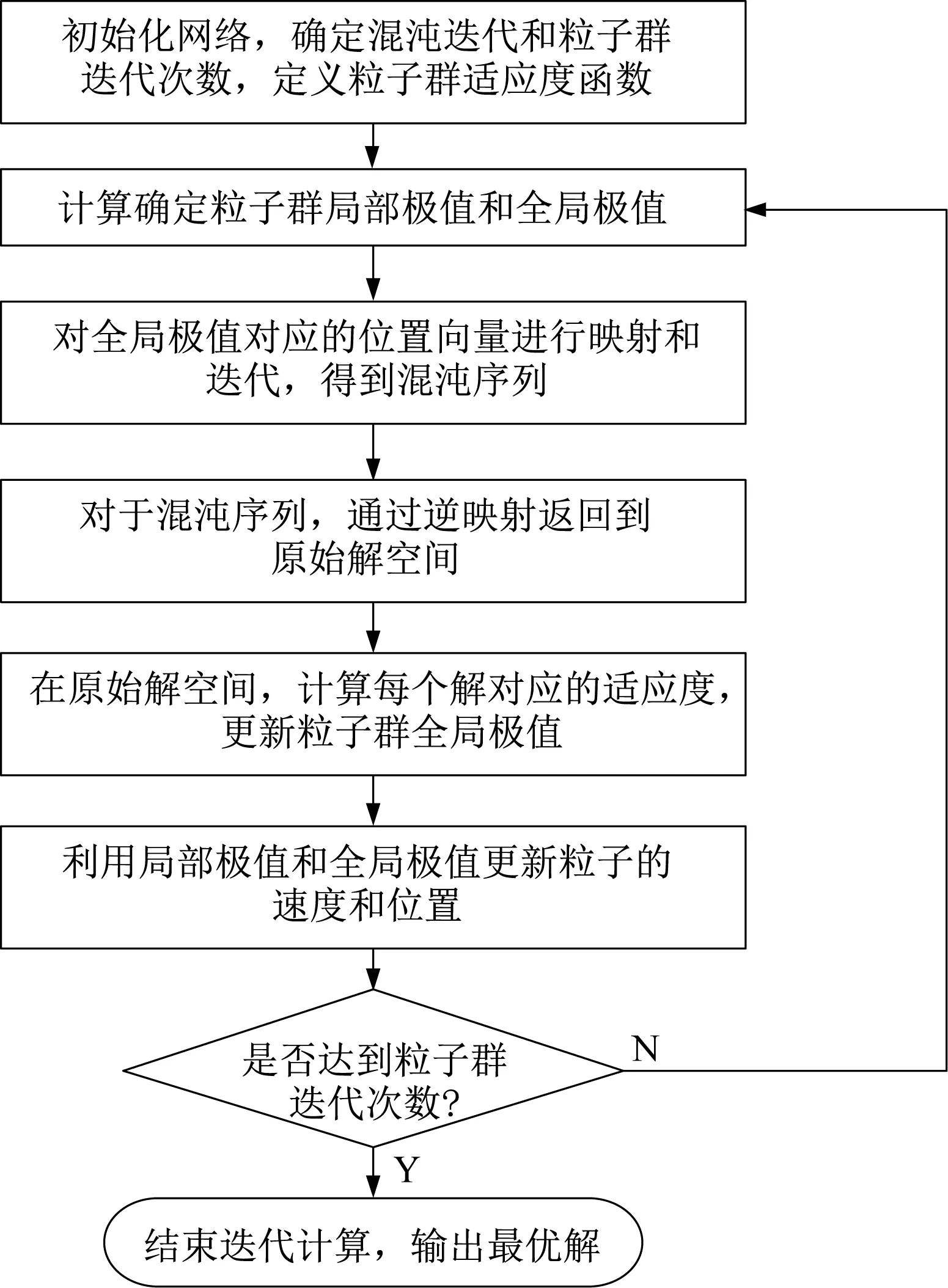
图2 小波神经网络训练流程
步骤1:初始化小波神经网络的层间权值以及小波层的尺度因子和平移因子,确定混沌迭代次数和粒子群迭代次数,定义粒子群的适应度计算函数,即
(6)
式中:N——网络的训练样本数;
O——网络输出;
d——目标输出;
p——网络输出和目标输出的维数。
步骤2:确定局部极值和全局极值。对于每一个粒子,比较其当前适应度与先前的最佳适应度(局部极值),并取二者中的较小值作为该粒子的局部极值。同时,取所有粒子当前适应度中最小值作为全局极值。
步骤3:对于全局极值对应的位置向量xg=(xg1,xg2,…,xgT),将其映射到区间[0,1],利用式(5)进行迭代,得到混沌序列。混沌序列通过逆映射返回到原始解空间,计算每个可行解对应的适应度,将最佳适应度对应的粒子随机替代群体中的一个粒子,同时最佳适应度保存为新的全局极值。
zt=(xgt-A)/(B-A) (t=1,2,…,T)
(7)
式中:xgt——位置向量的第j维分量;
A、B——xgt取值范围的最小值和最大值。
步骤4:进行迭代计算,每次迭代中,利用步骤3得到的局部极值和全局极值,分别按照式(8)和式(9)更新粒子的速度和位置。
vij(k+1)=wvij(k+1)+s1d1[Qij(k)-xij(k)]+
s2d2[Qgj(k)-xij(k)]
(8)
xij(k+1)=xij(k)+vij(k+1)
(9)
式中:vij、xij——第i个粒子速度向量和位置向量的第j维分量;
Qij——第i个粒子局部极值的第j维分量;
Qgj——全局极值的第j维分量;
w——惯性权重系数;
s1、s2——加速常数;
d1、d2——随机数,其取值区间[0 1]。
步骤5:当达到粒子群迭代次数时,结束迭代计算,输出最优解。
2 电能质量扰动信号分类仿真试验及分析
2.1 电能质量扰动信号模型
本文采用的信号数学模型包括正常电压和电压骤升、电压骤降、电压中断、暂态脉冲、暂态振荡、谐波、电压闪变共7种扰动信号[15],均通过MATLAB产生,电能质量扰动信号如图3所示。其中,电压工频周期为0.02 s,信号采样周期为1/3 ms。
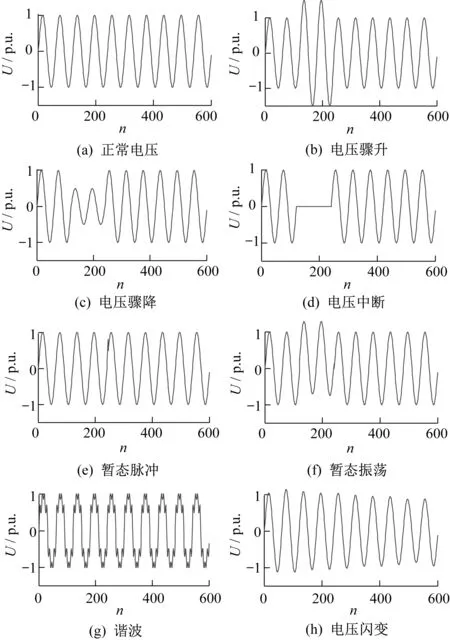
图3 电能质量扰动信号
2.2 小波神经网络构建
从小波神经网络结构可以看出,网络结构输入层的神经元个数由信号长度决定,故网络输入层的神经元个数确定为600。对待分类各信号进行编码,分别用000、001、010、011、100、101、110、111分别表示正常电压、电压骤升、电压骤降、电压中断、暂态脉冲、暂态振荡、谐波、电压闪变,则可确定网络输出层的神经元个数为3。
小波神经网络中,小波层的小波函数须满足有时域解析式的条件。根据各小波函数特点,本文选取Morlet小波对应的小波函数h(t),即
(10)
式中:w0——Morlet小波的中心频率。
本文选取中心频率w0=10 rad,Morlet小波时域波形如图4所示。

图4 Morlet小波时域波形
为加快网络的收敛速度,小波层参数的初始值按照以下原则选取。
由奈奎斯特采样定理可以得到Morlet小波的采样频率fSampling和最大频率fmax必须满足:
fSampling≥2fmax
(11)
其中,采样频率fSampling=1 Hz,最大频率fmax可取为1.25/aHz。根据式(11)可以得到a≥2.5。另外,当数据窗长度K给定时(本文为600),尺度因子a与数据窗长度K又满足如下关系:
a·Δt≤K-1
(12)
式中: Δt——Morlet小波的时窗宽度,取8。
由式(12)得到a≤74.875。故尺度因子aj的初始值为一组2.500~74.875的随机数。
对于平移因子bj,其初始值按式(13)计算。
bj=jK/J
(13)
式中:J——小波层的神经元个数。
小波层结构方面,如果神经元个数过少,则信号的特征无法得到充分表征,如果神经元个数过多,则网络的泛化性能会降低。本文采用试错法确定小波层神经元个数。经过反复调试,小波神经网络的小波层神经元个数确定为10。根据文献[16]可知,当隐含层神经元个数与小波层神经元个数相等时,网络的分类准确率最高,因此网络隐含层的神经元个数也确定为10。根据以上分析,本文搭建的4层小波神经网络的结构为600-10-10-3。
2.3 分类结果及分析
本文选取正常电压以及7种电能质量扰动信号各70组作为训练样本,另外选取正常电压以及7种电能质量扰动信号各100组作为检验样本。
网络训练时,为保证迭代计算精度,同时兼顾迭代计算耗时,粒子群的大小为m=50,粒子速度更新公式中的加速常数为s1=s2=2,粒子群的最大迭代次数为500,混沌的迭代次数为50,惯性权重系数w按下式更新:
w(t)=wmin+(wmax-wmin)(tmax-t)/tmax
(14)
式中:t——当前迭代数;
tmax——最大迭代次数;
wmin、wmax——w最小值和最大值,分别为0.4、0.9。
利用训练样本对网络进行训练,每次粒子群迭代时,对其适应度取以10为底的对数,粒子群训练误差曲线如图5所示。

图5 粒子群训练误差曲线
对于训练好的网络,将检验样本输入进行分类,各信号分类结果如表1所示。
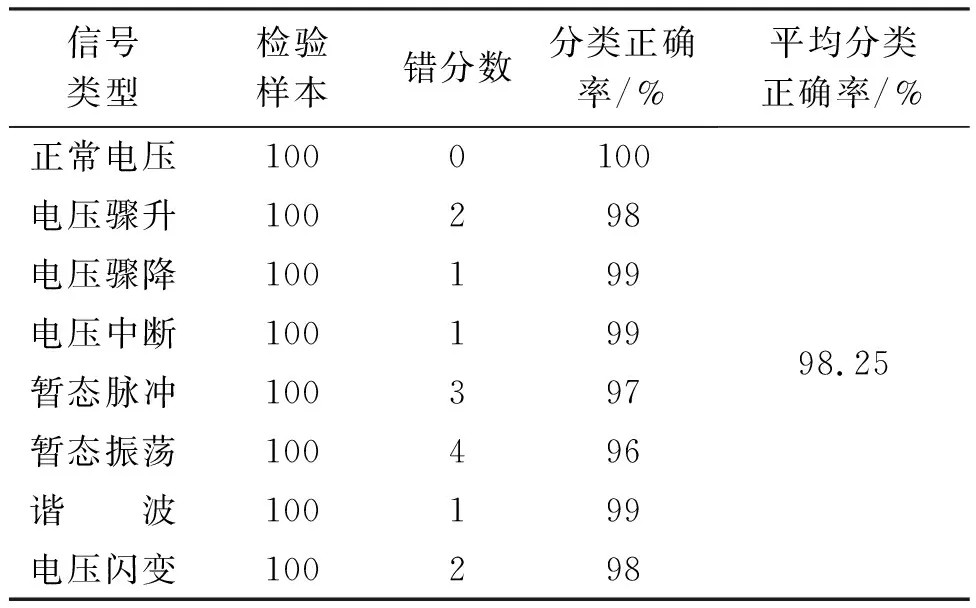
表1 各信号分类结果
由表1可见,混沌粒子群优化小波神经网络对正常电压、电压骤升、电压骤降、电压中断、暂态脉冲、暂态振荡、谐波和电压闪变的分类正确率分别为100%、98%、99%、99%、97%、96%、99%、98%,平均分类正确率为98.25%,表明混沌粒子群优化小波神经网络能够有效对电能质量扰动信号进行分类。
3 进一步分析
3.1 优化算法抗干扰性和稳定性分析
为了研究提出方法的抗干扰性和稳定性,分别向各信号叠加不同强度(方差)的高斯白噪声,形成信噪比分别为20 dB、30 dB、40 dB的含噪信号。选取正常电压以及7种电能质量扰动信号各70组作为训练样本,选取正常电压以及7种电能质量扰动信号各100组作为检验样本。不同信噪比含噪信号分类结果如表2所示。
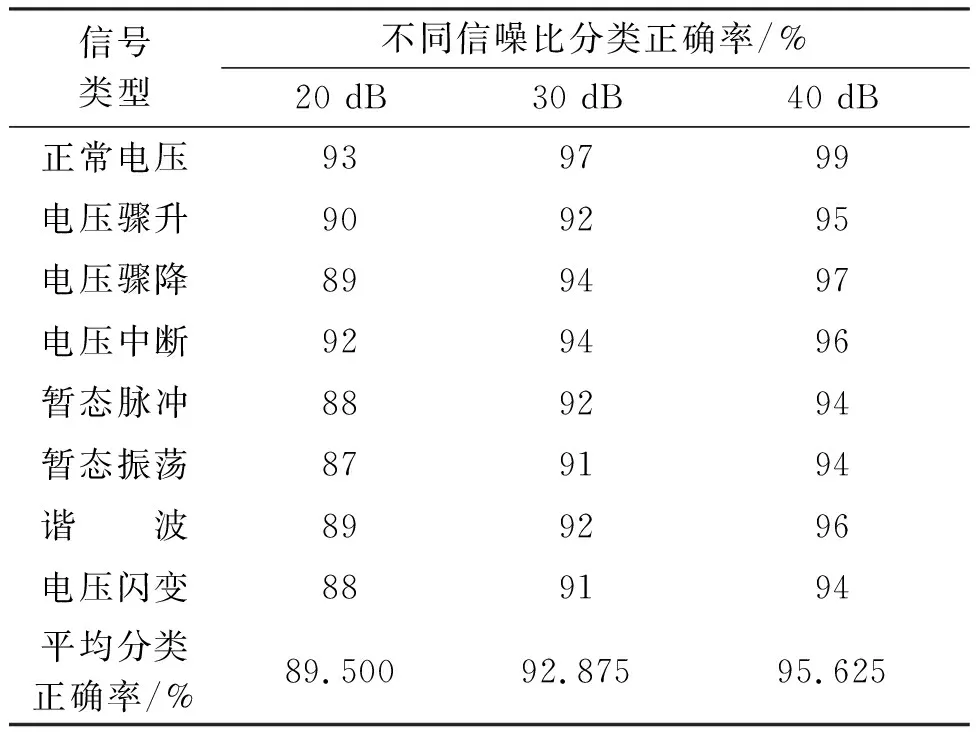
表2 不同信噪比含噪信号分类结果
由表2可见,随着噪声强度加大,即含噪信号的信噪比减小,本文提出方法对各信号的分类正确率和平均分类正确率减小,平均分类正确率分别为89.5%、92.875%、95.625%。由表2还可见,当噪声强度最大时,即信噪比为20时,暂态振荡的分类正确率最小(87%),但仍接近于90%,表明使用本文提出的方法对电能质量扰动信号进行分类时,受噪声的影响较小,稳定性好。
3.2 不同优化算法的分类结果对比分析
作为对比,本文选取2.3节的训练样本和检验样本。将检验样本输入到训练好的网络,不同优化算法的信号分类结果如表3所示。
由表3可见,相比BP算法和粒子群优化算法,使用本文提出的方法对小波神经网络进行训练,每种电能质量扰动的分类正确率以及总的平均分类正确率更高。
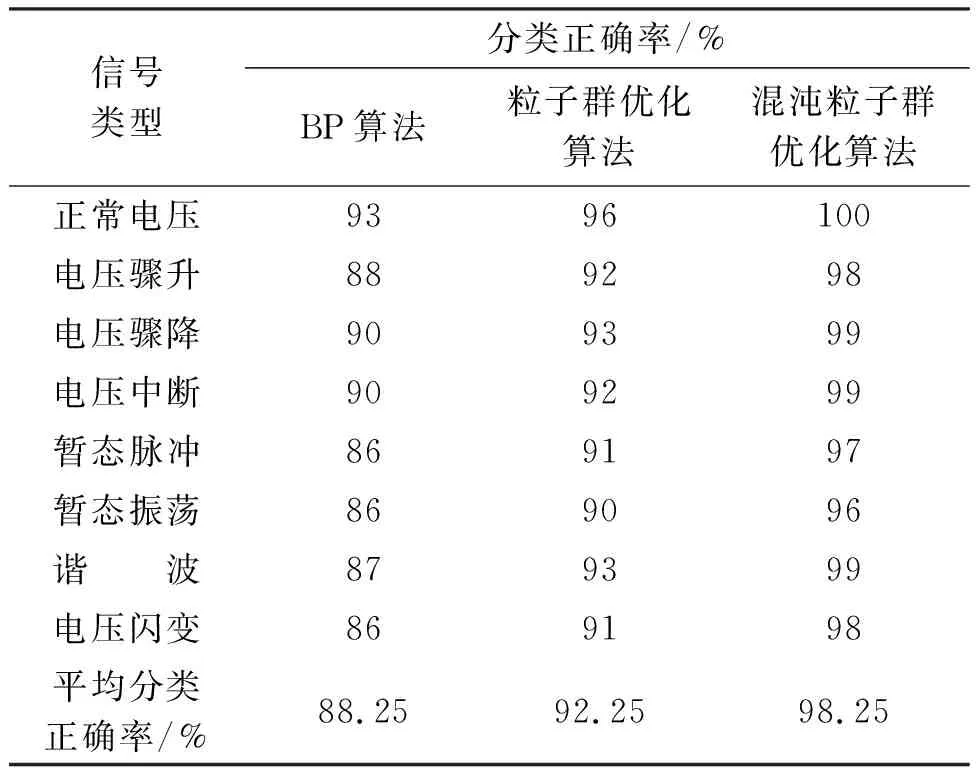
表3 不同优化算法的信号分类结果
4 结 语
为对电能质量扰动信号进行更加正确的分类,本文基于神经网络,利用小波函数作为网络隐含层的传递函数,构建了4层小波神经网络结构模型。使用训练样本对网络进行训练,检验样本对训练好的网络进行检验,得到以下结论:
(1)对不含噪声的正常电压和7种电能质量扰动信号的分类结果表明,混沌粒子群优化小波神经网络能够有效对各信号进行分类,平均分类正确率达到98.25%。
(2)对不同信噪比的含噪正常电压和7种电能质量扰动信号的分类结果表明,使用混沌粒子群优化小波神经网络对各信号进行分类时,具有抗干扰性强,稳定性好的优点。
(3)对比分别使用BP算法和粒子群优化算法对不含噪声的正常电压和7种电能质量扰动信号的分类结果表明,混沌粒子群优化小波神经网络能够对电能质量扰动信号更好地分类,具有更高分类正确率。
