基于参数辨识的固体电蓄热时滞系统建模与动态矩阵控制设计*

邢作霞, 苏 健, 付启桐, 刘 洋, 王晓奇,2

[1.沈阳工业大学, 辽宁 沈阳 110870; 2.延锋彼欧(沈阳)汽车外饰系统有限公司, 辽宁 沈阳 110020]

0 引 言

“大力发展新能源”是实现能源可持续发展的关键任务。然而,自2010年以来,我国风电弃风现象尤为严重。储能技术在电网调峰方面具有巨大的优势,其中储能设备固体电蓄热装置供暖可充分消纳弃风电量,其运行机制就是通过风电场与固体电蓄热装置的“绑定”模式,在用电低谷时段将弃风电量转换成固体电蓄热装置的热能存储起来,提高上网电量,避免浪费弃风电量。在供暖用户需求时供热,从而达到移峰填谷减少弃风的目的,有益于电网调峰。固体电蓄热装置供暖是规模化消纳弃风、促进清洁供暖的有效途径[1-3]。

目前,国内外温度控制系统主要采用PID控制,但固体电蓄热温度控制系统具有时滞性、大惯性、干扰因素多等特点。且用单纯的机理建模无法用公式准确地描述蓄热与换热的内在耦合过程,会直接造成建模误差,从而导致整个固体电蓄热供暖系统的温度控制失稳。文献[4]提出考虑供热系统多重热惯性的电热联合协调优化模型,研究了固体电蓄热体实际物理模型,并建立了热惯性模型。文献[5]提出电热微网能量梯级利用优化模型,使用MATLAB平台建立系统优化运行模型并求解最优运行方案。文献[6]集中供热二次网回水温度的预测和控制研究,建立了温控系统的数学模型,并设计了3层前向型神经网络与PID相结合的智能控制器,实现对二次网回水温度的闭环控制。然而,以往的研究工作者大多集中关注于电热耦合的物理模型及其广泛应用的PID控制技术,但随着科技的发展,大数据处理和基于数据的系统参数辨识,采用实时性的数据处理方式被应用于各个领域。

因此,本文提出了一种基于参数辨识的固体电蓄热时滞系统建模与动态矩阵控制设计。首先对固体电蓄热装置进行系统参数辨识建模,然后应用动态矩阵算法对固体电蓄热装置循环风量-水温控制系统进行调控,借助MATLAB仿真软件分别对传统PID控制和动态矩阵控制下的供暖出水温度模型进行仿真,并对二者的性能指标进行对比分析,最后应用固体电蓄热试验平台进行仿真验证。

1 固体电蓄热装置及电热耦合传热模型

固体电蓄热装置的供暖系统主要由固体电蓄热装置、外部供暖循环系统、供暖用户,还包括一些供暖附属设备补水箱、循环水泵等组成。其中固体电蓄热装置的主体是蓄热体;换热器以及循环变频风机。采用的是电阻加热方式,把电能转换为热能,通过辐射换热、对流换热方式把热量传递并存储到储热材料蓄热镁砖中,当需要利用这部分热量时,通过对流换热方式将空气加热,空气流经汽水换热器将热量供给到供暖系统。通过控制变频风机的工作频率来控制供暖出水温度,即循环风量-水温控制。固体电蓄热装置供暖系统示意图如图1所示。

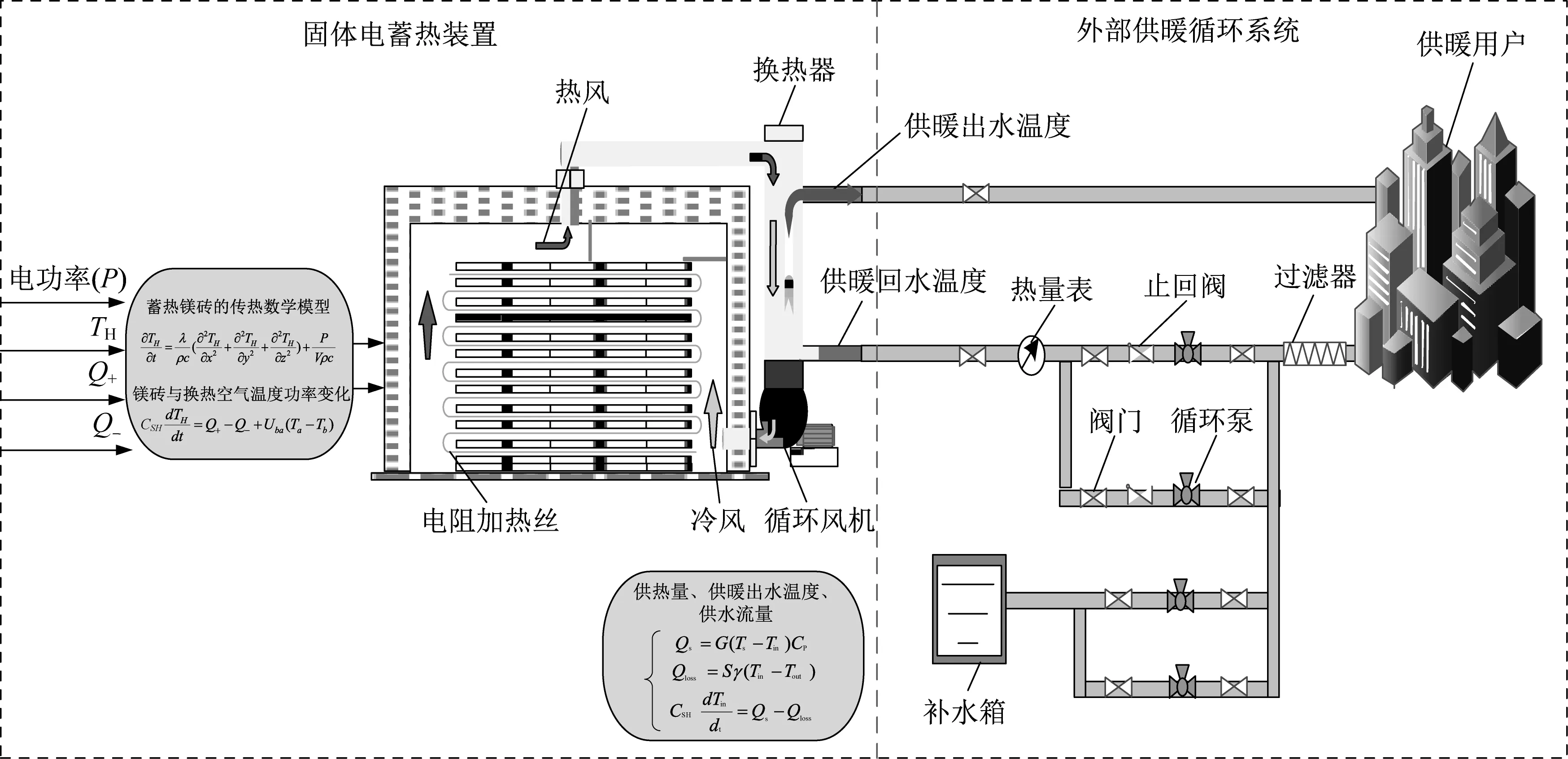
图1 固体电蓄热装置供暖系统示意图

固体电蓄热装置是将电能以热能形式的储热过程[7]。

(1)固体电蓄热装置的蓄热镁砖的传热数学模型为

(1)

式中:TH——蓄热镁砖温度;

λ——热导率;

P——电蓄热装置用电功率;

V——蓄热体体积;

ρ——蓄热镁砖密度;

c——蓄热镁砖的比热容。

(2)根据固体电蓄热装置的蓄热及放热原理,在蓄热和放热的过程中,改变耗电功率和换热器的循环风量,可以实现对电蓄热装置蓄热及放热惯性的调节[8]。

固体电蓄热装置的蓄热镁砖和换热空气温度的功率变化可描述为

(2)

式中:CSH——电蓄热装置总的比热容;

Q+——电阻加热丝对蓄热镁砖的加热功率;

Q-——电蓄热供暖系统的供热功率;

Uba——换热空气与外界环境的热导;

Ta、Tb——外界环境和换热空气温度。

(3)电蓄热供暖系统的供热量与供暖出水温度及供水流量的关系:

(3)

式中:Qs——电蓄热装置的供热量;

G——供水流量;

Ts——供暖出水温度;

CP——水的比热容;

Tin、Tout——建筑物室内、外温度;

Qloss——热损;

S——供热面积;

γ——室内热损失系数。

2 基于数据的系统参数辨识建模

目前,常用的系统建模有3种:对过程内在机理进行分析的机理建模;利用系统的输入输出数据建立模型的系统辨识,简称“黑箱”建模;以及将先验知识和系统辨识结合在一起的“灰箱”建模。由于固体电蓄热供暖系统是一个具有时滞性,并带有大惯性和强耦合等特点的系统,单纯的机理建模无法用公式准确地描述蓄热与换热的内在耦合过程,为避免造成建模误差,在对电蓄热原理有一定了解的基础上,采用“灰箱”建模的方法。系统参数辨识流程如图2所示。

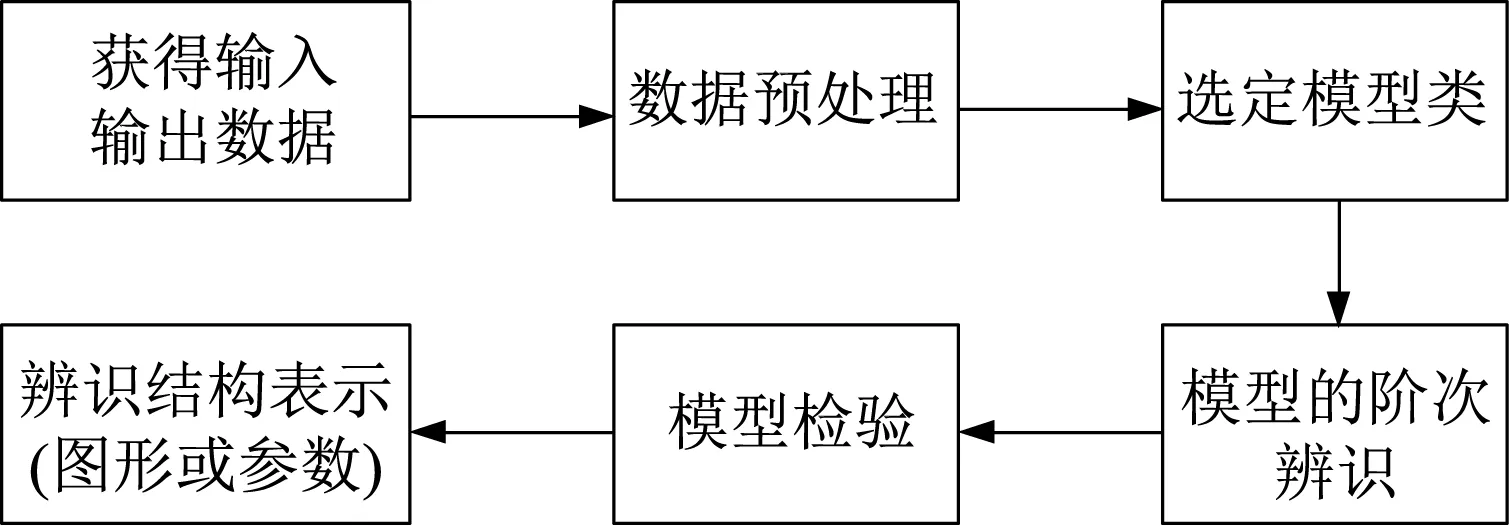
图2 系统参数辨识流程

2.1 系统参数辨识模型结构

固体电蓄热循环风量-水温控制系统中,辨识对象是变频风机控制的循环风量,输出是供暖出水温度。大多数的温度控制系统可用一阶或二阶系统加纯滞后环节来描述,其数学模型可为

(4)

其中,b1≠0,a1、a2、b1、b2为时变未知参数,需在线辨识;d为系统延时阶数,可看作已知。

式(4)写成离散的差分方程形式:

A(z-1)y(k)=z-dB(z-1)u(k)

(5)

式中:k——采样时刻;

u(k)——系统输入循环风量;

y(k)——系统输出供暖出水温度。

(6)

在对控制系统建模时,温度控制系统通常采用一阶或二阶系统来表征其特性,模型阶次的增加并不能保证控制效果的好坏,如采用三阶或更高阶来描述时不仅其意义不大[9-10],而且在控制器设计方面也会加大难度,影响控制效果,不失一般性,本文的固体电蓄热供暖系统也是一个温度控制系统,由文献[11]可知,模型的阶次采用一阶系统表征更好。

d为系统延时阶数,供暖出水温度控制下,供暖距离较短,因此滞后时间d较小,时滞时间可分别取d=1、d=2、d=3,对固体电蓄热供暖系统进行系统参数辨识。不同延时阶数下供暖出水温度模型辨识误差如图3所示。由图3可明显看出,d=1时误差较小,因此本文采用一阶延时系统。

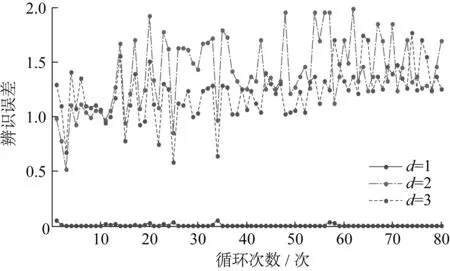
图3 不同延时阶数下供暖出水温度模型辨识误差

2.2 系统参数辨识结果

取辽宁省鞍山某地区固体电蓄热装置供暖系统云平台循环风量及供暖出水温度监控数据,采用下面2种辨识方法进行系统参数辨识。

2.2.1 最小二乘递推法

利用MATLAB系统辨识工具箱(System Identification),分别将循环风量和供暖出水温度数据导入input与output序列,然后对其做数据预处理,最小二乘递推法采用多项式模型中的ARX模型[12-14],将过程扰动的影响看作相关噪声,采样周期为60 s,得到的辨识模型参数如下:

(7)

试验数据与最小二乘辨识模型输出如图4所示;最小二乘辨识模型的温度辨识误差如图5所示。由图4和图5可以看出,辨识的结果与试验数据基本吻合,温度辨识误差在±0.3 K以内。

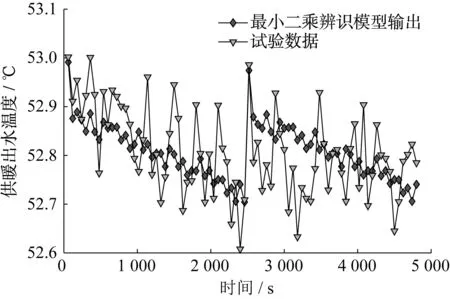
图4 试验数据与最小二乘辨识模型输出

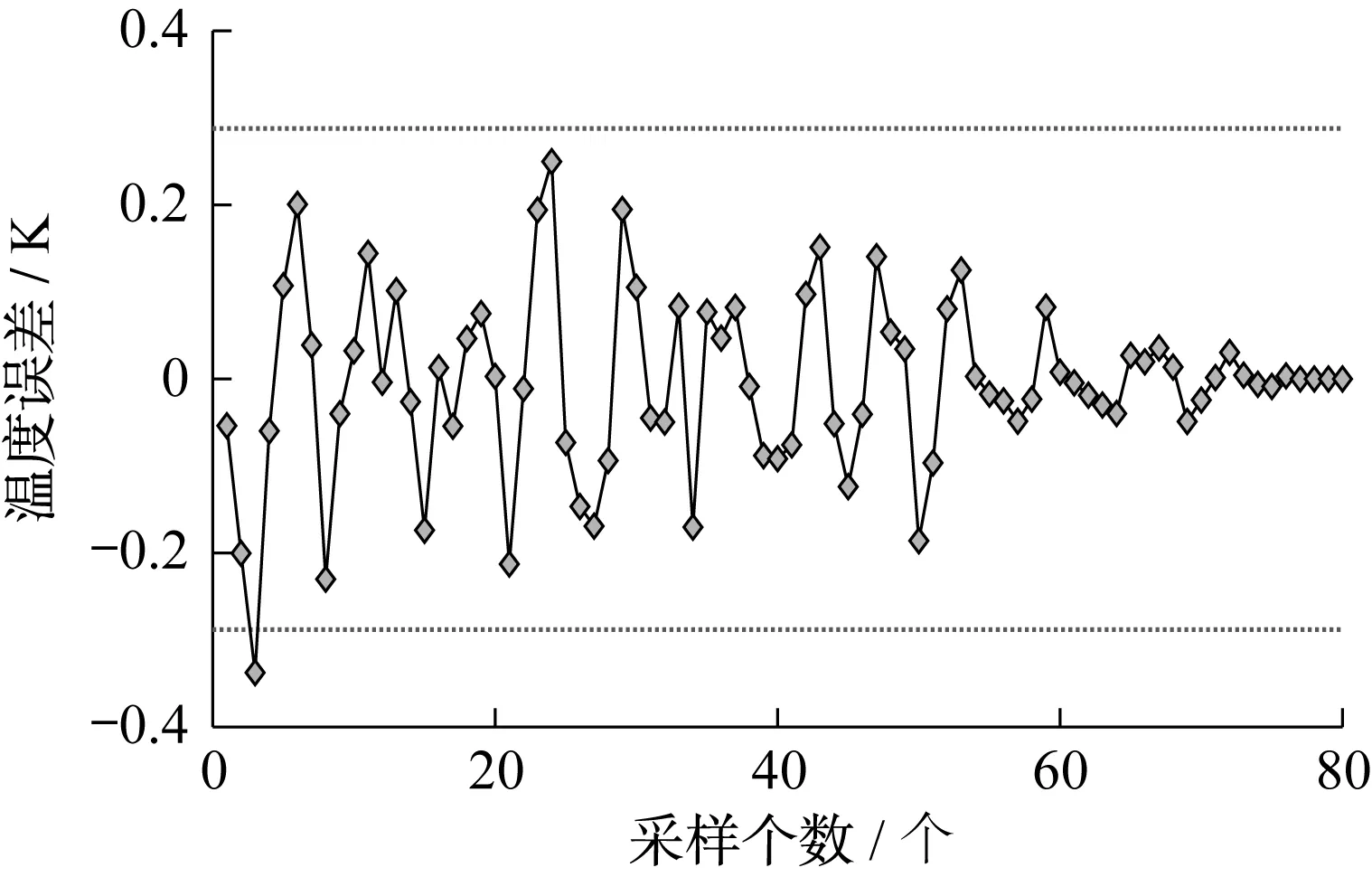
图5 最小二乘辨识模型的温度辨识误差

2.2.2 辅助变量递推法

同理,辅助变量递推法采用多项式模型的IV模型,采样周期为60 s,得到的辨识模型参数如下:

(8)

试验数据与辅助变量辨识模型输出如图6所示;辅助变量辨识模型的温度辨识误差如图7所示。由图6和图7可以看出,辨识结果与试验数据基本吻合,温度辨识误差大部分在±0.3 K以内,但个别情况会超过±0.4 K。

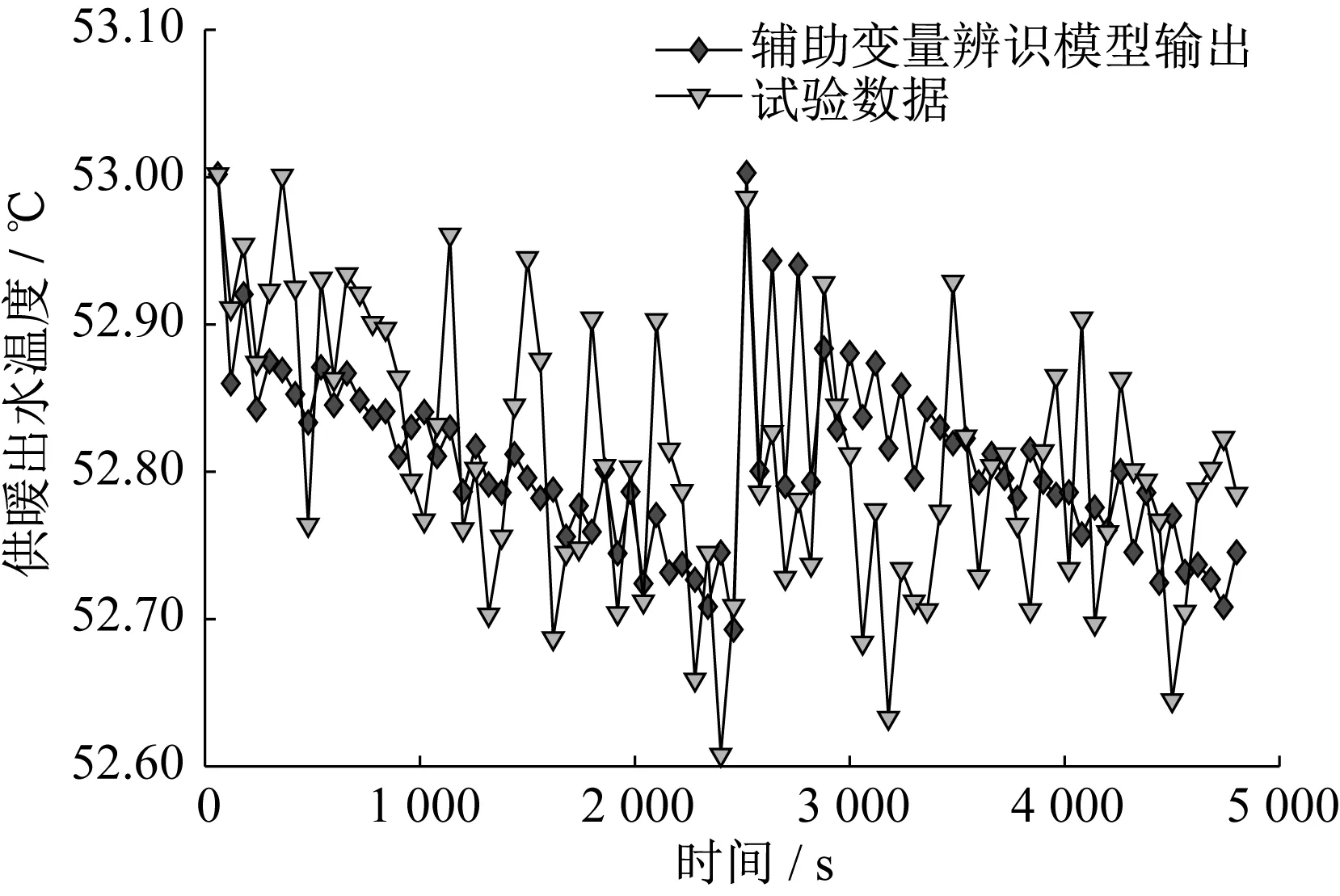
图6 试验数据与辅助变量辨识模型输出

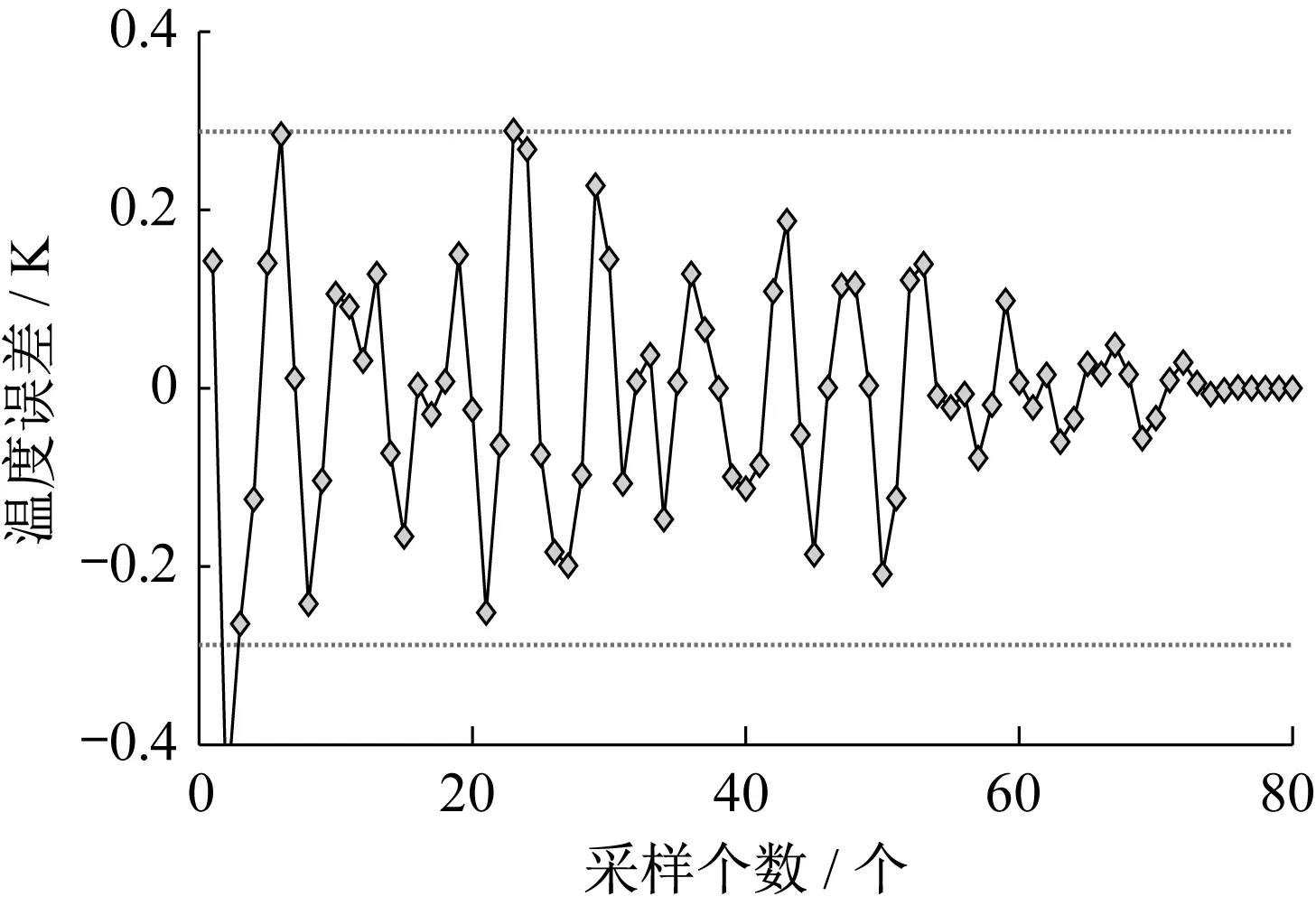
图7 辅助变量辨识模型的温度辨识误差

最小二乘辨识与辅助变量辨识误差对比如图8所示。由图8可见,最小二乘辨识误差大部分都比同一时间的辅助变量辨识误差小,且辅助变量辨识偶尔会出现误差较大的个别情况。因此最小二乘递推法更适用于固体电蓄热循环风量-水温控制系统的模型参数辨识。

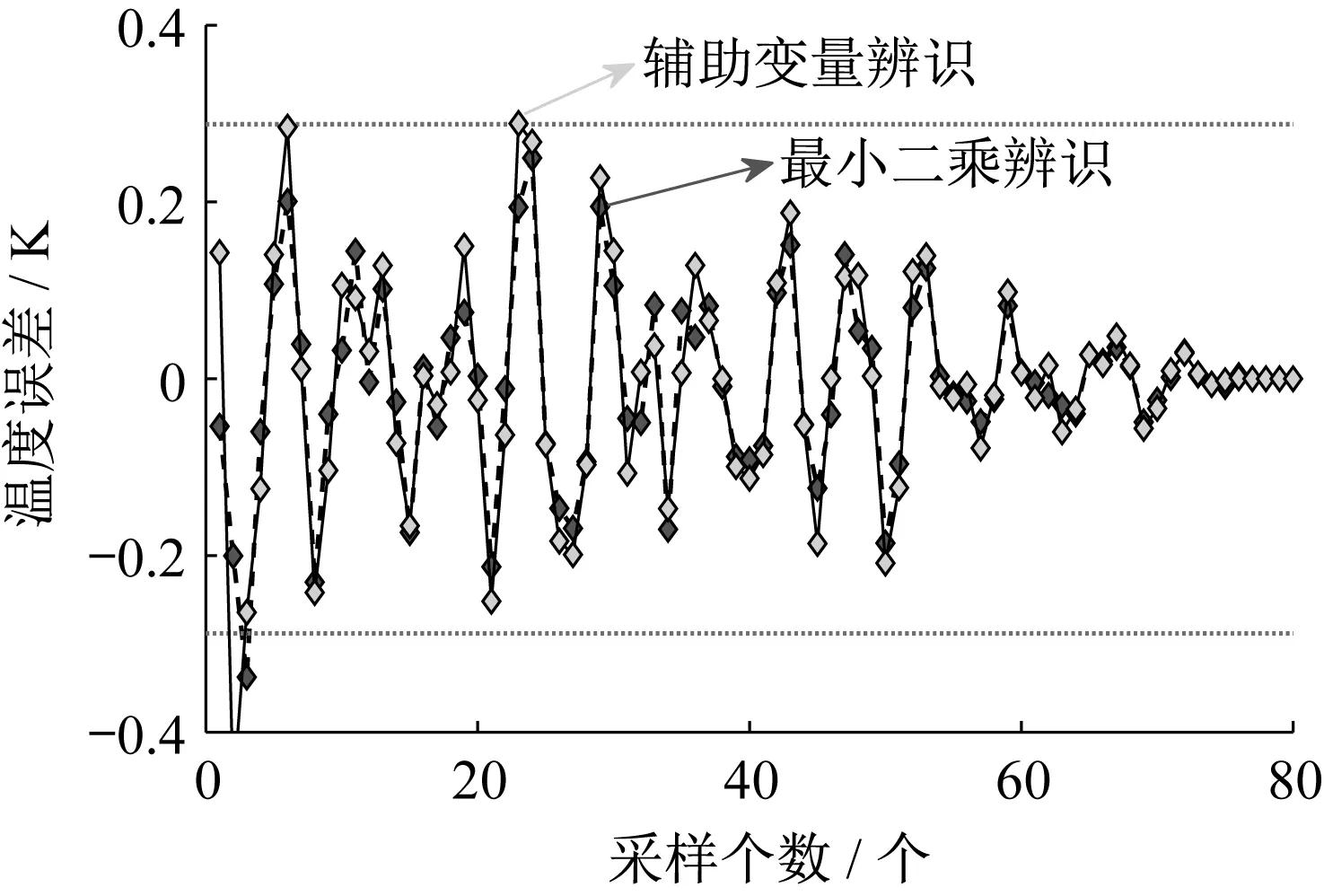
图8 最小二乘辨识与辅助变量辨识误差对比

3 基于动态矩阵的固体电蓄热循环风量-水温控制

动态矩阵控制算法是利用过程模型预测系统在人为控制下将要发生的动态行为,并且根据已知的约束条件及要求,通过滚动优化和反馈校正优化当前与未来时刻的控制量,使系统输出曲线尽可能与设定的参考轨迹相符[15-17]。因此,动态矩阵一般分为预测模型、滚动优化以及反馈校正3个主要部分。

3.1 预测模型

首先测定控制对象供暖出水温度的单位阶跃响应的采样值ai=a(iT),i=1,2,…,N。其中,T为采样周期,N为模型时域长度。根据线性系统的比例和叠加性质,在t=kT时刻,假如控制作用保持不变,在未来N个时刻的供暖出水温度的输出预测值为

y0(k+i|k),i=1,2,…,N

(9)

其中:k+i|k表示在t=kT时刻预测t=(k+i)T时刻。那么,在k时刻加入循环风量的控制增量Δu(k)作用后,在未来N个时刻的供暖出水温度的输出预测值为

(10)

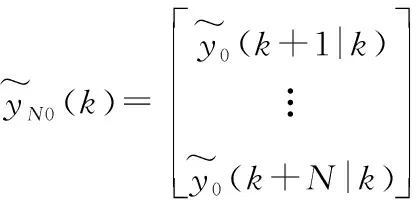
如果控制增量在未来M个釆样间隔都在变化,则在t=kT时刻预测在控制增量Δu(k),Δu(k+1),…,Δu(k+M-1)作用下系统在未来P个时刻的输出为

(11)

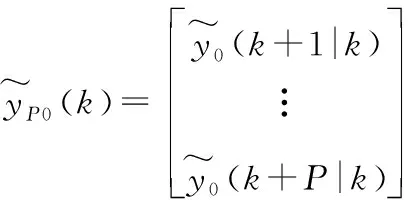
3.2 滚动优化

滚动优化一般可分为调节与跟踪两大问题。调节问题,首先确定从某一时刻开始的未来M个控制增量,然后在控制增量的作用下,尽最大可能地使未来P个时刻的输出预测值近似于设定的期望值。跟踪问题,确定从某时刻开始的M个控制增量,尽可能地使输出预测值能够跟踪期望轨迹。

3.3 反馈校正

在建立控制系统的预测模型时,通常采用的模型参数a只是控制系统的粗略模型。必要的作法是引入动态校正环节,利用差值实时对预测值进行校正,即

Yp(k+1)=Ym(k+1)+h(y(k)-ym(k))=

A0U(k-1)+AU(k)+he(k)

(12)

其中,Yp(k+1)=[yp(k+1),yp(k+2),…,yp(k+p)]T,e(k)=y(k)-ym(k),h=[h1,h2,…,hp]T。

式中:Yp(k+1)——系统的供暖出水温度预测矢量;

e(k)——预测模型的供暖出水温度误差;

h——误差修正系数矢量。

基于动态矩阵控制算法的固体电蓄热循环风量-水温控制如图9所示。

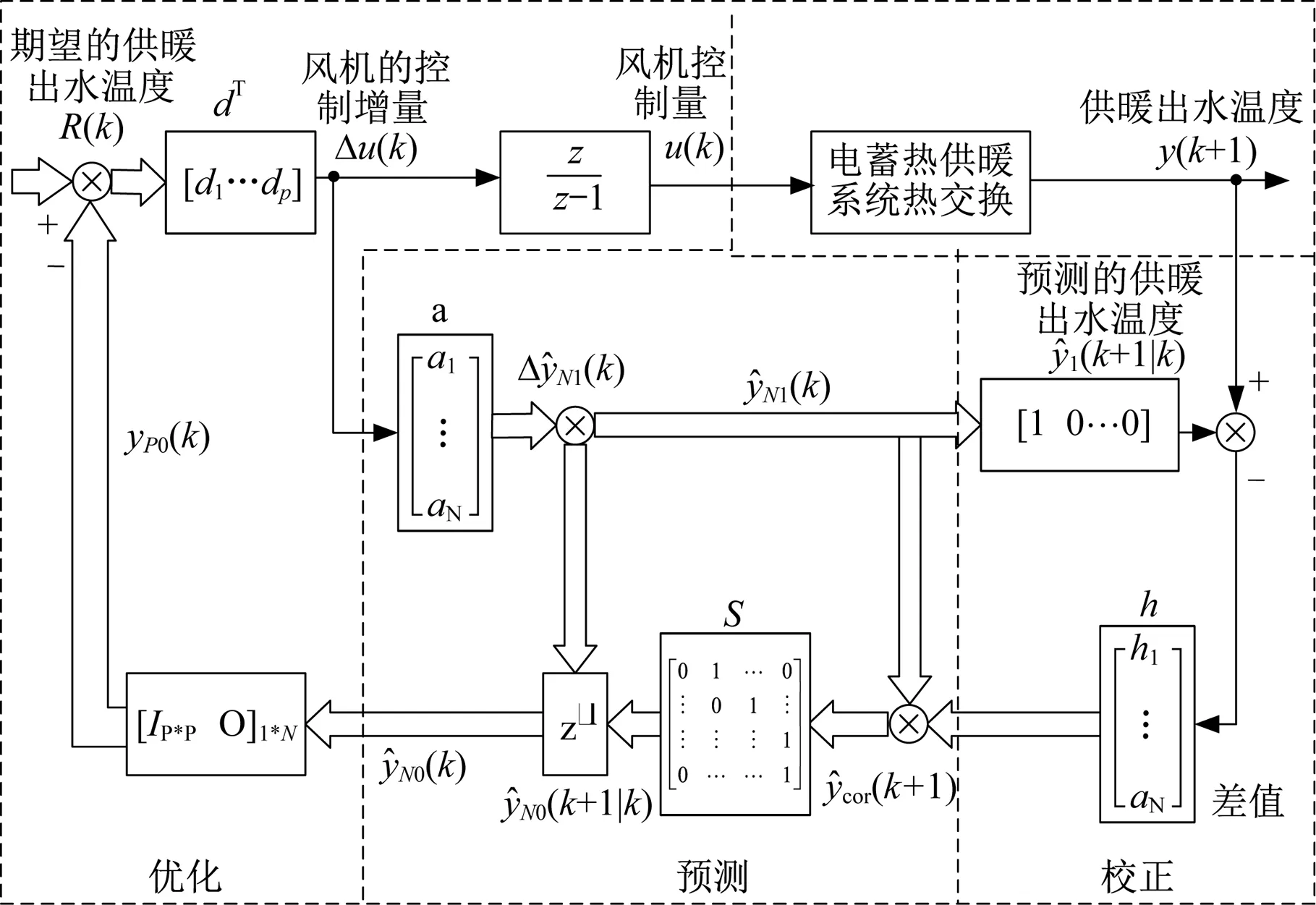
图9 基于动态矩阵控制算法的固体

4 动态矩阵在固体电蓄热循环风量-水温控制系统的仿真及验证

4.1 PID控制算法仿真

采用PID控制算法对被控对象G(z)在阶跃响应下进行仿真,由于PID参数的整定十分复杂,通过经验试凑得到PID控制器在P控制、PI控制和PID控制下的比例放大系数Kp、积分时间常数Ti以及微分时间常数Td的值。设定期望的供暖出水温度为53 ℃,采样周期Ts=10 s,系统在PID控制时运行仿真,得到最佳阶跃响应曲线,PID控制参数为Kp=8,Ti=0.03,Td=1。P控制、PI控制和PID控制供暖出水温度如图10所示。

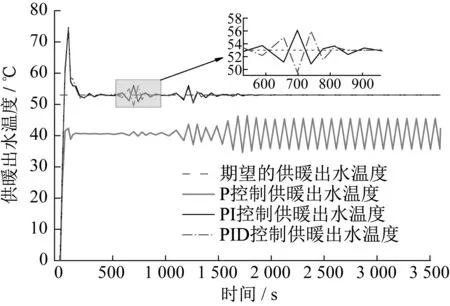
图10 P控制、PI控制和PID控制供暖出水温度

4.2 动态矩阵控制算法仿真

采用动态矩阵控制算法对被控对象G(z)在阶跃响应下进行多次仿真,取得最优控制效果时的输出曲线,此时的控制参数采样周期Ts=10 s,模型时域长度N=5000,预测时域长度P=6,控制时域长度M=2。动态矩阵算法控制供暖出水温度如图11所示。

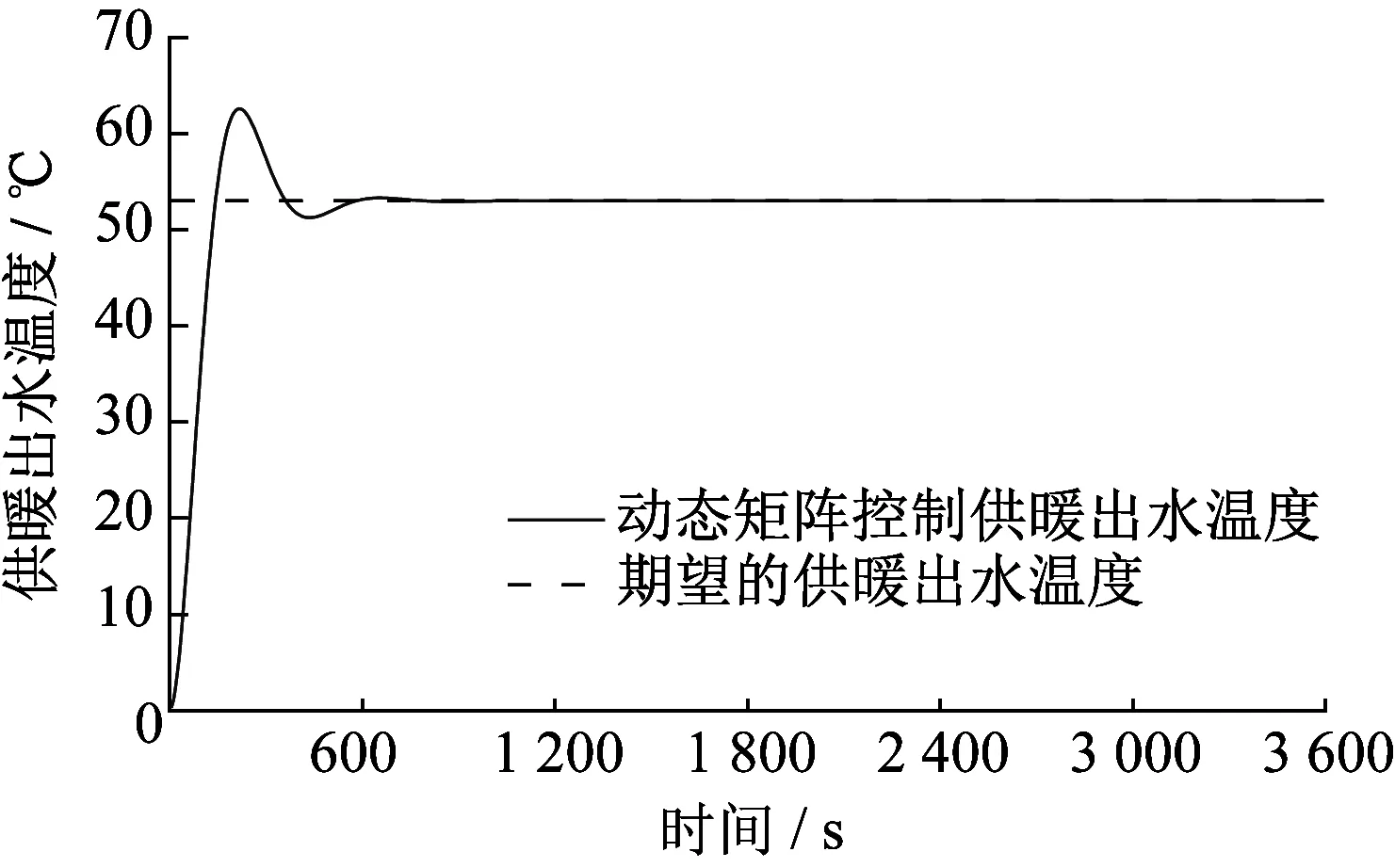
图11 动态矩阵算法控制供暖出水温度

4.3 仿真结果对比分析

对动态矩阵控制与PID控制下的阶跃响应曲线仿真结果进行对比分析。动态矩阵控制与PID控制对比如图12所示。PID控制的最大超调量达到了74.348 31,动态矩阵控制的最大超调量为62.472 8,且由小图可以看到当动态矩阵控制达到稳定后,PID控制还会出现波动,因此动态矩阵控制要比PID控制先行达到稳定状态。结果表明,在PID控制算法下系统达到稳定的时间较长,且超调量相对较大,控制效果并不理想;而在动态矩阵控制算法下系统达到稳定的时间较短,超调量相对较小,系统振荡较小,控制效果更优[18-20]。

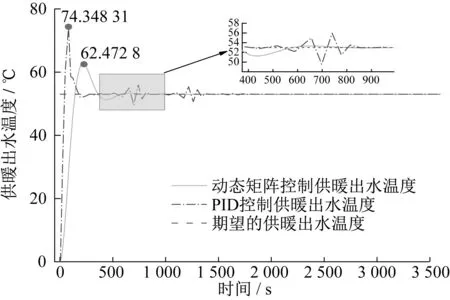
图12 动态矩阵控制与PID控制对比

4.4 实验验证

在现有的固体电蓄热装置试验平台上,对固体电蓄热供暖控制系统进行了相关研究,包括对固体电蓄热供暖系统的系统参数辨识建模、控制器设计和MATLAB环境下控制策略仿真验证。为保证电蓄热装置安全稳定的供暖,在整个供暖过程中对供暖出水温度或供暖回水温度、循环风量等物理量进行在线监测和实时采集,并上传到电蓄热供暖云平台上,方便对电蓄热供暖系统进行实时监控和数据分析处理。实验时首先要接通加热丝的电源,调整好预设的期望供暖出水温度53 ℃,开始对装置进行加热,待加热一段时间后系统稳定,每隔1 min读取一次供暖出水温度数据。并进行固体电蓄热装置供暖系统未进行参数辨识建模的原系统PID控制与参数辨识建模下的动态矩阵控制的供暖出水温度对比。固体电蓄热装置试验平台如图13所示;参数辨识建模的动态矩阵控制、PID控制与原数据对比分析如图14所示。

图13 固体电蓄热装置试验平台

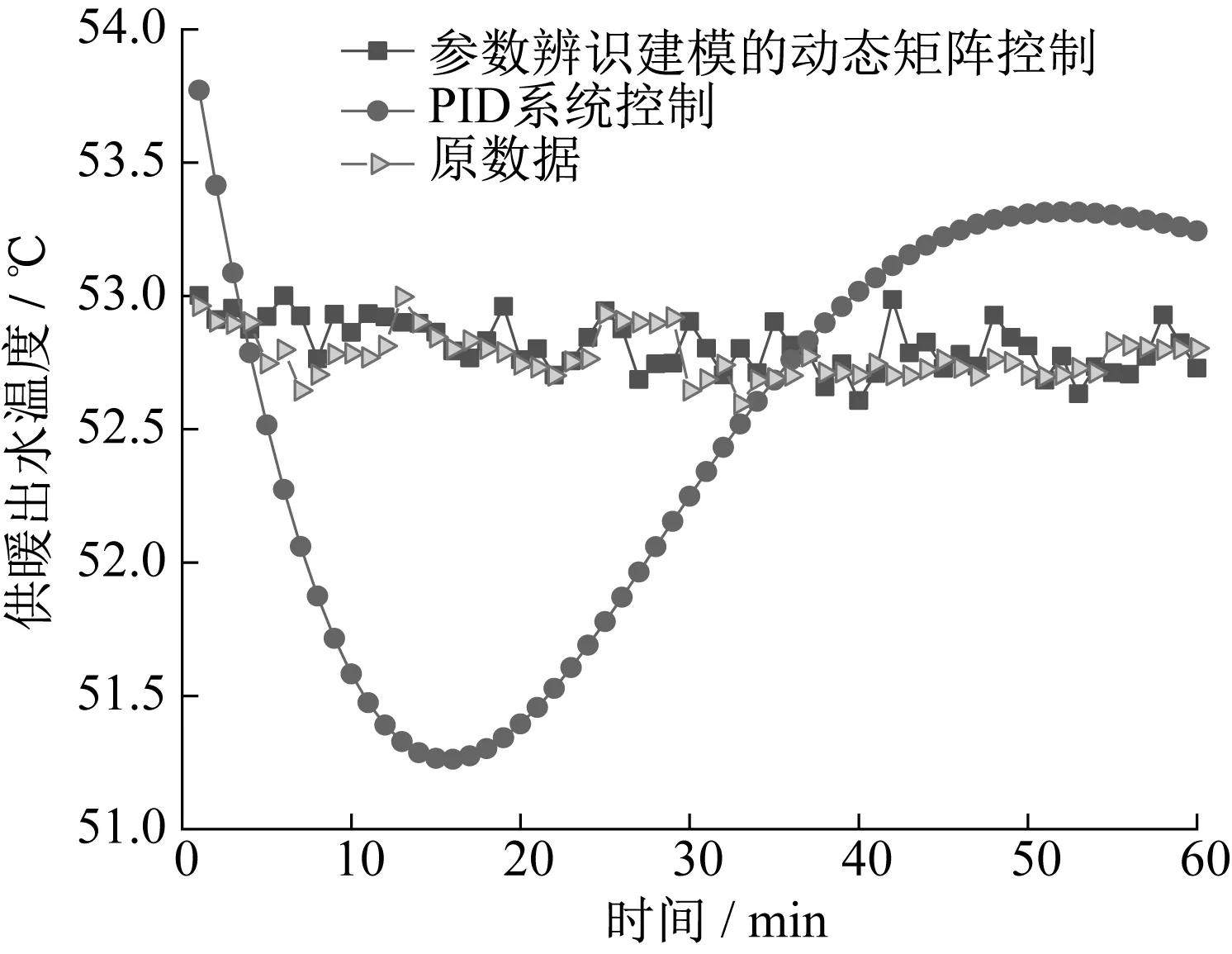
图14 参数辨识建模的动态矩阵控制、PID控制与原数据对比分析

参数辨识建模的动态矩阵控制实验测得的供暖出水温度与期望的供暖出水温度53 ℃基本吻合,但是两者之间仍存在较小的误差,原因可能是实际装置中各物理参数存在偏差和实验过程中可能产生的测量误差,但原系统PID控制实验测得的供暖出水温度与期望的供暖出水温度相差较大。通过上述仿真计算与实验结果的对比,表明基于参数辨识的固体电蓄热时滞系统建模与动态矩阵控制设计方法的正确性。

5 结 语

本文针对固体电蓄热循环风量-水温控制系统在温度控制信号和温度检测反馈信号之间存在很大的滞后时间,且无法用单纯的机理建模来描述蓄热与换热的内在耦合过程。因此采用基于数据的系统参数辨识建模,建立了更加精确的固体电蓄热时滞系统数学模型,并提出了基于动态矩阵的固体电蓄热循环风量-水温控制策略,以辽宁省鞍山某地区固体电蓄热装置供暖系统为例进行仿真及实验验证,结果表明:

(1)基于数据的系统参数辨识建模最小二乘递推法比辅助变量递推法辨识误差更小,预测的模型输出与试验数据更加契合,能得到更加精确的数学模型。

(2)与原系统PID控制算法相比,基于参数辨识建模的动态矩阵控制超调量更小、调节时间更短、稳态误差更小,具有较强的稳定性和鲁棒性,控制效果更佳。可用于解决固体电蓄热循环风量-水温控制系统的大惯性、时滞性问题,实现对固体电蓄热装置供暖出水温度的智能控制,保证供暖用户的供暖质量。