小型断路器双金属片热弯曲特性的实验仿真
2022-04-28潘庆元
潘 庆 元
(北京ABB低压电器有限公司, 北京 100176)
0 引 言
双金属片是由两种或多种具有不同热膨胀系数的金属或其他材料轧制而成的一种复合材料,常被用作低压电器的热脱扣机构核心元件。其在小型断路器、继电器、开关、控制器等产品中都得到了广泛的应用。
从20世纪90年代起,我国就有学者做过双金属片计算性能方面的理论研究[1],其采取的理想假设条件简化了计算,但同时也降低了精度,得到的结果可以初步划定参数选择范围,后续仍需要大量试验数据进行进一步筛选。虽然最终也能够得到较好的结果,但通常会花费大量的人力、物力和时间成本。这也是长期制约国产双金属元件品类迭代及其推广应用的重要因素之一。
随着现代计算理论和能力的发展,仿真分析被广泛应用于各个工程领域。近年也有同行运用有限元方法对导电回路进行温度场分析[2],但以双金属片设计开发为导向的仿真分析很少报道。
1 影响双金属片性能因素
影响双金属片热弯曲性能的因素众多,其中双金属片组元层设计是其性能好坏的关键。双金属片性能的影响因素如图1所示。
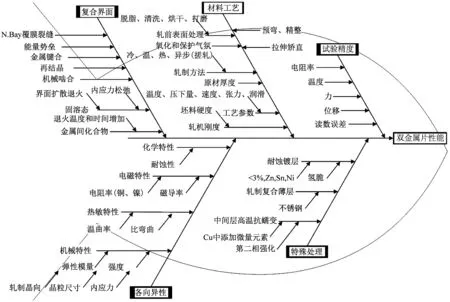
图1 双金属片性能的影响因素
本文以小型断路器热脱扣用双金属片为研究对象,联合使用理论计算、有限元仿真、试验设计等方法,建立了3层双金属片弯曲特性仿真平台,为双金属片元件参数设计及优化提供了低成本、高效率且相对准确的分析工具。
2 双金属片优化设计流程
传统的双金属片的设计流程是通过试验设计获得不同厚度材料的一组热弯曲性能,这种方法目标离散度大,虽然采用DOE方法可以缩小搜索范围,但试验成本仍然较高,此时得到的是比弯曲等材料特性。而在应用端,更希望得到的是不同形状的双金属材料对应的受热变形状态及力学特征。对于简单长条造型、功能单一的使用情况,通常使用理论和经验公式可以得到近似结果;而对于造型复杂的情况,则只能通过试制样件来逐步分析和优化。这无疑进一步增加了产品的开发成本。因此,希望使用非线性求解及有限元方法代替其中大部分试验内容,从而减小开发成本,缩短开发周期。
双金属片优化设计流程图如图2所示。

图2 双金属片优化设计流程图
3层双金属片优化设计流程如下:通过查询资料及材料性能试验获得单质材料的材料属性(包括电阻率、弹性模量、泊松比、线膨胀系数等)。将材料属性代入电阻率平衡方程、厚度方程、比弯曲方程组成的方程组,设定目标值,可求得单层厚度解。由于方程组是非线性的,求解使用数值方法,需要代入校验公式对结果的精度进行验证。如果精度不足,则对上述过程中的输入数据进行调整(如重做材料性能试验等);如果精度足够,则将所得厚度结果、材料属性及元件具体造型作为初始数据输入有限元仿真,可以得到阻挡力、功能区域的挠度等仿真结果。将仿真结果与性能试验及理论计算结果做对比,如符合度较高,则证明所建立的双金属片热弯曲特性仿真平台有效,将来可以使用平台工具进行新型双金属片元件的开发和选用,用以部分代替前期试验。
本文结合已有产品的小型断路器热脱扣用双金属片的性能参数进行仿真和验证。
3 材料属性数据
当额定电流流过双金属片时,电阻率和散热情况决定了温度升高的快慢[3],而组元层厚比和热膨胀系数又决定了随着温度升高,元件弯曲的程度。
小型断路器采用较高的热膨胀系数材料用作主动层或称高膨胀层(HES),根据成分不同,一般分为CuNiMn系列和FeNiMn(或FeNiCr)系列[4]。其中Mn72Ni10Cu18、FeNi20Mn6应用较为广泛,常用于高敏感电阻型热双金属[5],价值相对中敏感性也偏高。Cu由于其良好的导电性常被用作分流层以调节电阻率,FeNi36由于极低的热膨胀系数常用于被动层或称低膨胀层(LES)[6-7]。双金属片常用材料的热膨胀系数、弹性模量、电阻率分别如图3~图5所示。
由图3~图5可见,大部分材料的属性呈现出与温度的非线性变化关系,传统公式中常取某一工作温度下的数值进行计算。这使得在制作出样品并进行性能试验前,人们对双金属片复合材料的全温度域热弯曲特性的认识是有限的。
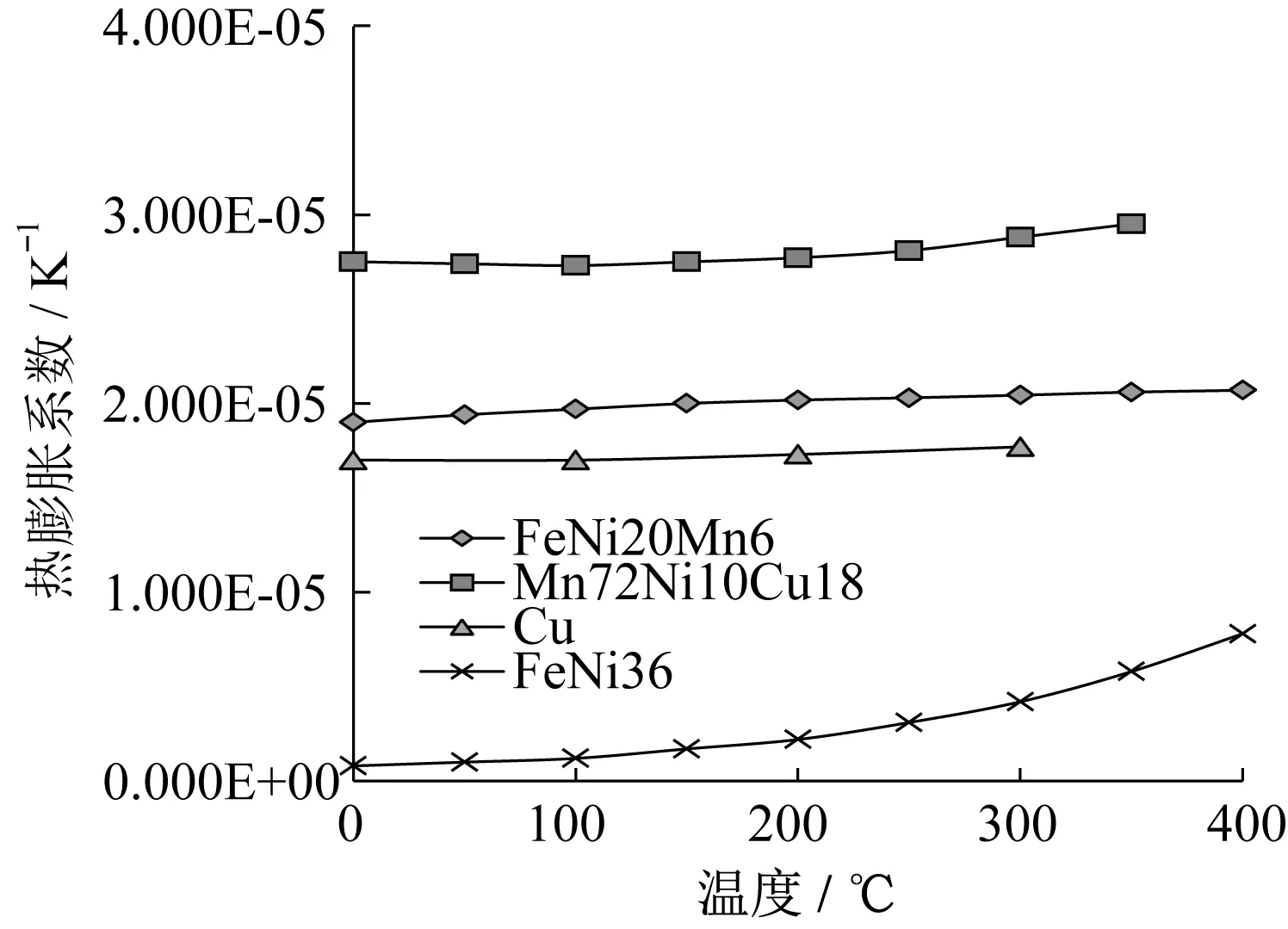
图3 双金属片常用材料的热膨胀系数

图4 双金属片常用材料的弹性模量

图5 双金属片常用材料的电阻率
4 双金属片组元层厚度比的数学模型
通过各组元层材料的合理选用和厚度比的适度调整,可满足系列化对牌号比弯曲高且各不同牌号比弯曲值基本接近的要求[8]。
4.1 双金属片组元层厚度比的方程组
假设各薄层各向同性,且忽略界面作用。3层双金属片的组元层厚度比可由以下总厚度、电阻率、温曲率等式组成的方程组来求解[9]。
(1)
其中,
M=12E1S1·E2S2·E3S3
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
式中:Si(i=1,2,3)——组元层厚度比;
Ei(i=1,2,3)——组元层弹性模量;
ρi(i=1,2,3)——组元层电阻率;
ρb——综合电阻率;
F——温曲率。
4.2 3层双金属片的综合弹性模量
假设各薄层各向同性,且忽略界面作用。3层双金属片的综合弹性模量Eb可以用下式求解:
(12)
(13)
式中:μi(i=1,2,3)——组元层泊松比;
μb——双金属片综合泊松比;
s——双金属片总厚度。
综合弹性模量的计算公式中引入了各组元层厚度,可以作为上一步求解结果的验算步骤。值得注意的是,无论是求解公式还是验算公式都提到了假设,在与实际测量数据核对时可能存在一定的误差。设定误差≤10%为可接受范围。
4.3 计算示例
某型号3层双金属片总厚度s=1 mm,在室温下的综合电阻率为0.11 Ω·mm2/m,弹性模量为165 GPa,比弯曲为27.8×10-6(1±5%)/K(此处取中值计算)。计算所得参数如表1所示。

表1 计算所得参数
从以上计算和验算结果可以看出,计算所得的组元层厚度值验算弹性模量与标称值的误差仅为2.8%。与判定指标对照,可接受。
5 理想状态下的理论计算与仿真
5.1 理想理论变形量
理想条件下,双金属温度分布是各处相同的。
5.1.1 简支梁状态下的热双金属片挠度计算
简支梁状态下热双金属片随温度变化弯曲如图6所示。
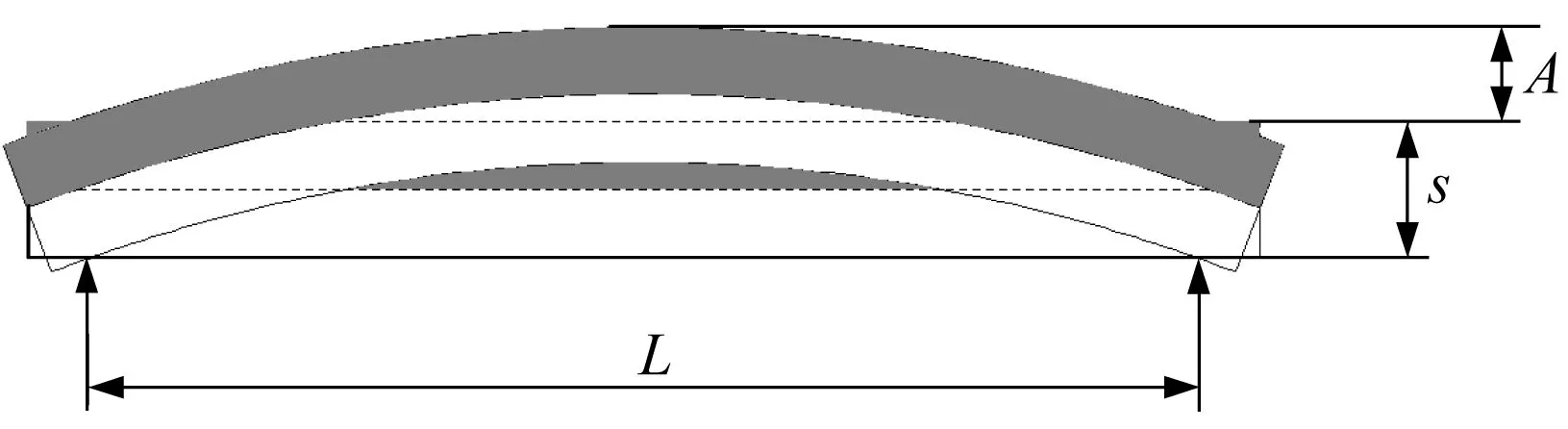
图6 简支梁状态下热双金属片随温度变化弯曲
对于已知热弯曲特性的常温下平直的长条形双金属片,约束一端点位移,另一端点滑动支撑,得到简支梁支撑状态,当温度升高时,中间拱起并在滑动支撑点受到反力[10-13]。简支梁状态对应于测量阻挡力实验时的受力和变形状态。此时的试样挠度A按下式计算。
(14)
式中:L——双金属片有效长度;
ΔT——试样弯曲时相对平直时的温度变化量;
F——温曲率。

(15)
设F=27.8×10-6/K,ΔT=178 K,L=29 mm,s=1 mm,得A=0.522 mm。
5.1.2 悬臂梁状态下的热双金属片挠度计算
悬臂梁状态下热双金属片随温度变化弯曲如图7所示。同样的长条形双金属片,将一端夹紧,得到悬臂梁支撑状态,当温度升高时另一端翘起。悬臂梁状态对应于测量自由位移实验时的变形状态。
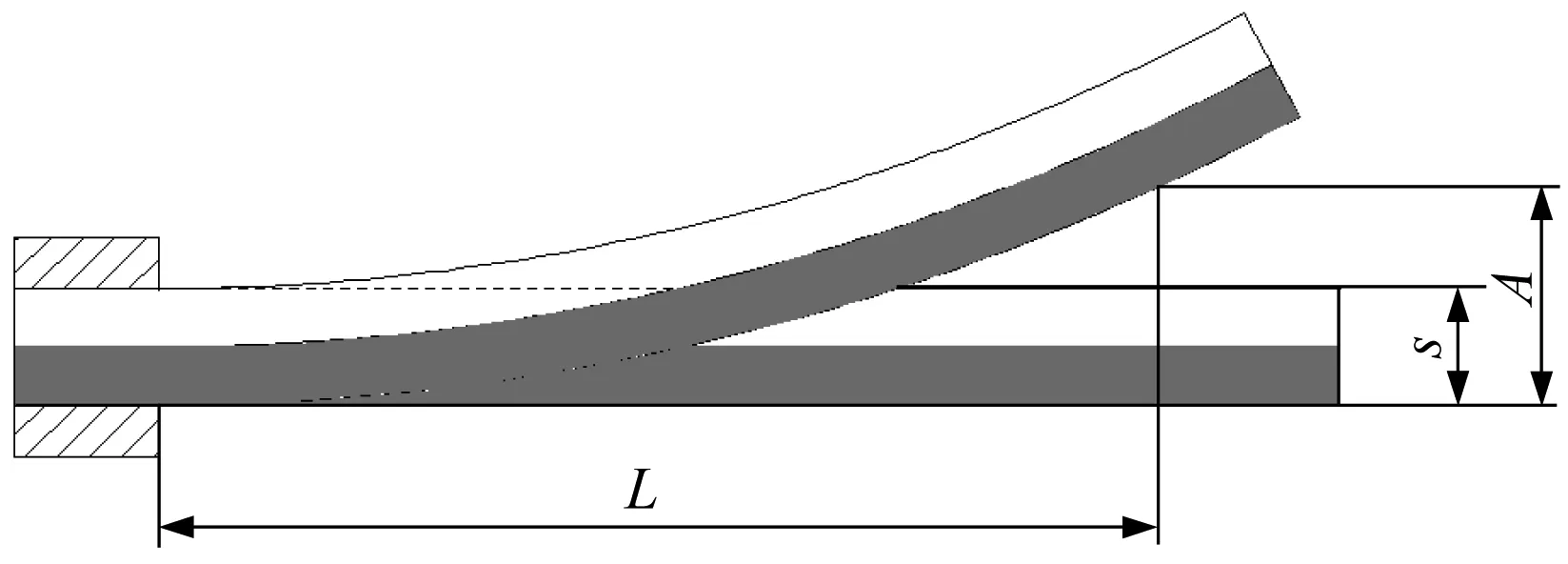
图7 悬臂梁状态下热双金属片随温度变化弯曲
此时的挠度A按下式计算。
(16)
式中:K——比弯曲。

(17)
由于夹持状态与简支梁不同,此时固定端占用6 mm,L=23 mm,K≈0.53F,得A=1.403 mm。
理想状况的理论公式中,假设双金属片各处温度均匀。但实际情况中,双金属片各处温度是变化的。有限元方法可以分别设置为理想和实际两种状态,并且可以快速地随意地切换,这可以体现出有限元方法的优越性。
5.2 理想简支梁和悬臂梁状态的校验
5.2.1 建立有限元模型
双金属片模型如图8所示。双金属片三维模型如图8(a),材料属性按照第3节的曲线设定。使用带中间节点的六面体单元/四面体单元划分网格,如图8(b)。

图8 双金属片模型
5.2.2 设置边界条件
按理论计算状态设置边界条件,其中温度场使用统一变量178 K。边界条件如图9所示。

图9 边界条件
5.2.3 计算
运行计算,得到2种边界条件下的变形结果。理想悬臂梁和简支梁的扰度如图10所示。
由图10可见,仿真结果与理论计算结果非常接近。这说明在均匀温度场条件下,有限元仿真

图10 理想悬臂梁和简支梁的挠度
结果和理论计算结果的精度是近似的。
6 试验条件下的力和位移及其仿真
6.1 双金属片热弯曲试验
6.1.1 试验设备及原理
双金属片热弯曲阻挡力、位移测量平台如图11所示。将双金属片固定在特制的夹具上后通电,随着温度上升,双金属片产生变形。当施加红宝石探针时,相当于简支梁,可通过测力传感器读出阻挡力数值;当不施加红宝石探针时,相当于悬臂梁,可通过激光测距仪读出双金属片测点位移。
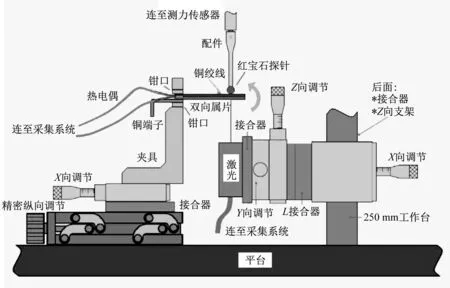
图11 双金属片热弯曲阻挡力、位移测量平台
6.1.2 样品的温度监测
双金属片在实际通电过程中,各处温度是有差别的。为了掌握具体的温度场分布情况,使用热电偶传感器在被测双金属片上分别添加5处温度监测点。温度监测点如图12所示。
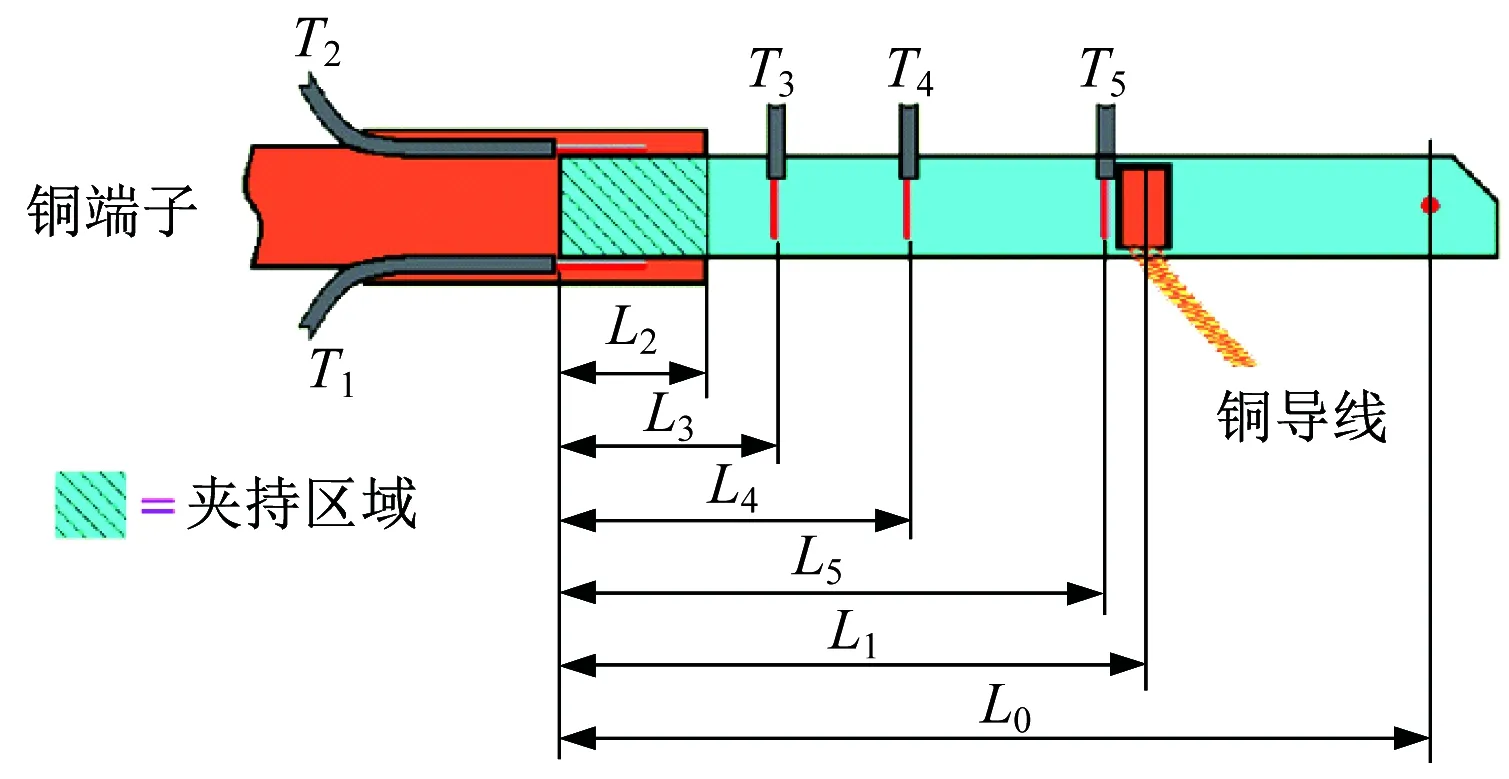
图12 温度监测点
图12中,Ti(i=1,2,3,4,5)为各处监测点温度;L0为双金属片热弯曲力和位移作用点到固定端的距离;L1为双金属片导电作用长度;L2为夹持长度;Li(i=3,4,5)为分别是温度监测点3、监测点4、监测点5到固定端的距离。
6.1.3 试验条件
试验在室温下进行,双金属片通电试验条件如表2所示,In为小型断路器额定电流。

表2 双金属片通电试验条件
6.2 对照试验的有限元求解
按照实验条件下各检测点温度随时间变化值,可以模拟出的温度场随时间变化的分布情况。试验条件下某一时刻温度场分布如图13所示。

图13 试验条件下某一时刻温度场分布
6.3 试验和仿真结果对比
相对于温度理论公式计算,试验和仿真能更直观准确地反映双金属片随温度变化的不同阶段的力和变形情况。试样5个测点的温度变化量如图14所示;试验和仿真的阻挡力如图15所示;试验和仿真的变形量如图16所示。从结果看,仿真数值与试验结果十分接近。其中注意到,在时间节点6时,试验结果较之仿真结果有较大偏离。分析认为双金属片在2.55In作用下急剧升温,其过程只有10 s,没有达到热平衡,贴片热电偶数据采集系统来不及采集数据所致。因此,该数据对仿真结果没有影响。

图14 试样5个测点的温度变化量
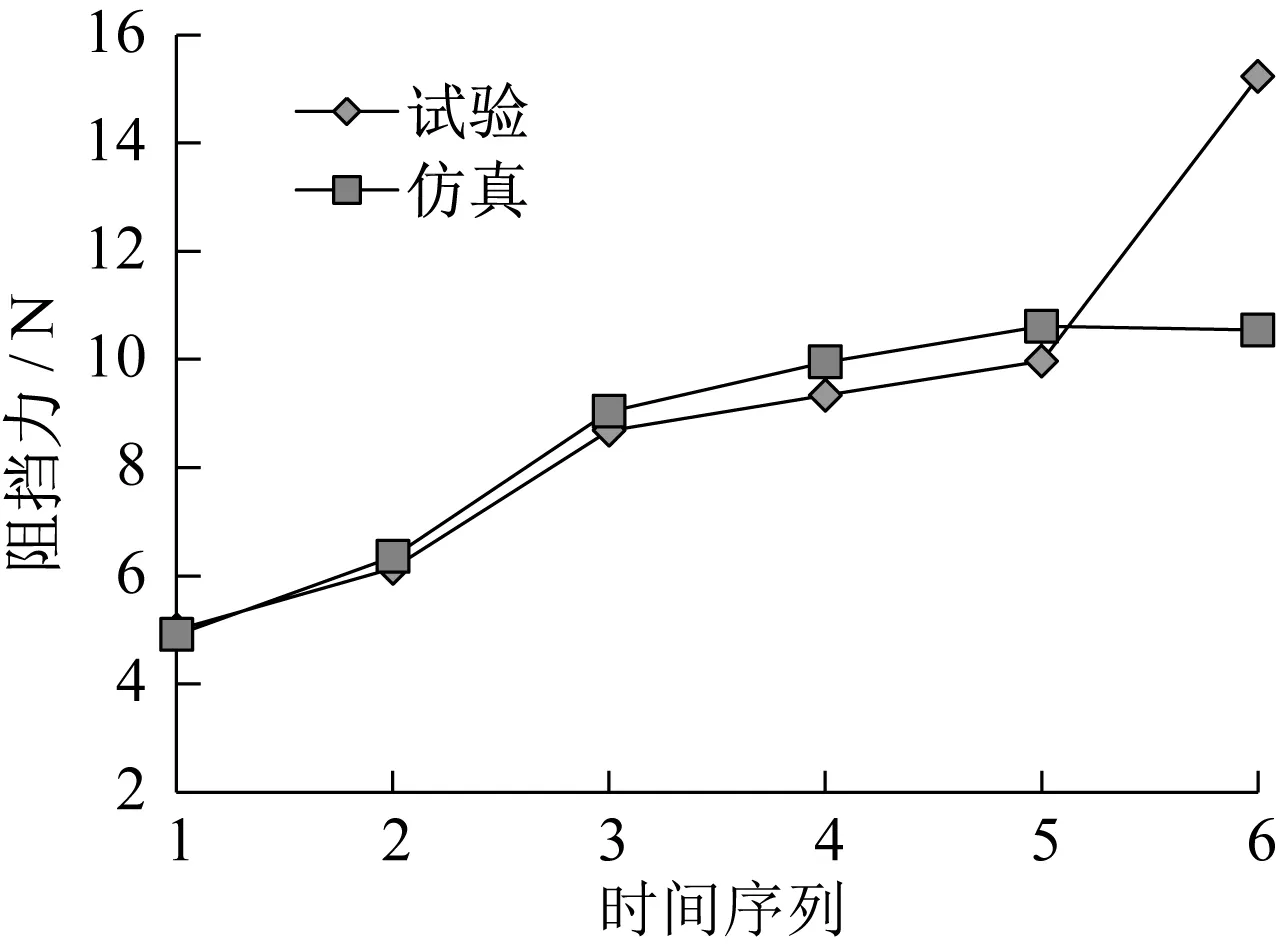
图15 试验和仿真的阻挡力
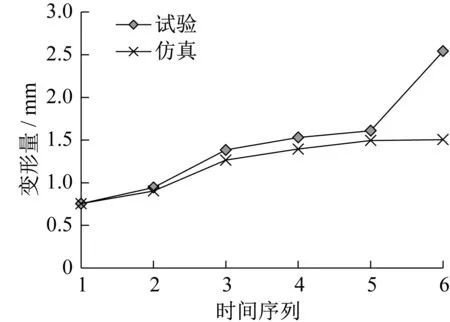
图16 试验和仿真的变形量
综合以上讨论,仿真平台可以较好地模拟小型断路器双金属片的弯曲特性。在优化设计时,可以利用仿真平台快速求解和验证双金属片设计参数,显著提高设计效率和可靠性。
7 结 语
本文以小型断路器热脱扣用双金属片为研究对象,分别从理论计算、试验分析和数值仿真等角度对热弯曲特性进行了分析,得出以下主要结论:
(1)提出了双金属片优化设计新思路,并以此为基础建立了双金属片热弯曲特性的仿真平台,为双金属片元件优化设计提供了便捷高效、准确可靠的工具。
(2)将理论计算公式程序化、自动化,输入目标性能参数,数值求解即可得到组元层厚度初值。
(3)有限元数值仿真能够考虑双金属片的真实温度场分布,相比理想理论公式更接近实际情况,其仿真结果更加准确可靠。利用仿真方法替代部分前期试验,能够减少研发成本,缩短开发周期。同时满足新产品开发设计和量产产品成本优化的需要。
(4)开发和设计了热双金属片弯曲性能试验专用成套夹具,完善了试验平台和方法。与仿真平台联合使用,通过试验设计可以进一步修正偏差,寻求双金属片设计参数最优解。
(5)仿真平台建立后,利用双金属片热脱扣力和脱扣行程的仿真结果,与小型断路器操作机构的设计指标比对,可进一步实现双金属片层结构参数与操作机构参数的协同设计[14],为产品早期参数设计和方案可行性评估提供了参考依据。
