共享储能模式下多微电网博弈优化方法*
2022-04-28郑海林温步瀛朱振山翁智敏
郑海林, 温步瀛,2, 朱振山,3, 翁智敏
(1.福州大学 电气工程与自动化学院, 福建 福州 350108;2.福建省新能源发电与电能变换重点实验室, 福建 福州 350108;3.智能配电网装备福建省高校工程研究中心, 福建 福州 350108)
0 引 言
电化学储能作为微电网的重要灵活性资源[1-3],通过合理的应用储能系统可以减少微电网偏差考核与峰时段的购电需求,提升经济效益[4]。目前阻碍储能商业化应用的原因主要是储能配置高昂费用[5-6]和频繁调度的成本[7]。近年来,共享经济模式已逐渐成为优化资源配置的新方向[8],有许多成功的案例诸如共享汽车、共享充电宝等。
文献[9]在可再生能源与共享经济迅速发展的背景下,提出了一种基于储能的云储能服务,以降低储能成本为共享储能模式的发展提供思路。文献[10]以社区综合能源系统为研究对象,提出了包含共享储能的用户协同优化模型,通过租赁的方式调用共享储能,但未能对共享储能配置高昂成本进行分析。文献[11]通过共享储能的应用以及可变电价市场机制来实现可再生能源的高渗透,但未能对共享储能的用户效益全面挖掘。文献[12-14]考虑了共享储能配置的高昂费用,以共享储能收益最大化为目标求解,但本质仍是在多个用电主体联合调度基础上优化储能容量的配置,并未能体现储能的共享特性。文献[15]考虑了储能的全寿命周期费用,基于不同售电公司的贡献度对共享储能的效益再分配,但未能充分考虑各参与主体调度意愿。
综上所述,现有关于储能配置的研究主要集中在独立的电能用户,缺乏共享经济理念在配置储能方面的应用,在少数共享储能文献中未能全面考虑不同用电主体之间的利益诉求不同,或未能综合考虑微电网中可中断负荷、火电机组以及电动汽车充电站等诸多灵活性资源对共享的影响。
针对上述不足,本文提出储能聚合商整合相邻微电网的储能资源,通过价格机制提高储能利用率以及各方的经济性。以运行效益最大化作为各微电网与储能聚合商优化目标,综合考虑各微电网内的火电机组、可中断负荷和电动汽车充电站等调度资源,计及不同投资主体利益诉求,提出了共享储能模式下多微电网博弈优化运行策略,采用多智能体强化学习算法求解,并引入Kullback-Leibler(KL)散度优化其学习率。
1 共享储能下微电网优化模型
微电网大多配置储能优化自身出力,提高运行经济性。因此针对多个已安装储能的微电网用户,通过储能聚合商整合储能资源,避免储能配置高昂成本,降低微电网的运行经济性,同时提升储能系统利用率。微电网配置储能的寿命周期成本由储能聚合商承担,当微电网需要调度储能优化自身出力时,则需要向储能聚合商支付一定的服务费用,并承担产生的充放电损耗费用,储能聚合商通过服务费用与优化调度从而获取收益。
1.1 微电网优化目标
本文中微电网的运行经济性包括可再生能源的运维成本、火电机组的燃料成本与爬坡成本[16]、可中断负荷与电动汽车充电站调度费用、购电成本以及调用储能支付的费用。微电网优化目标函数为微电网运行成本Fmg:
Fmg=CRE+CMT+CIL+CEV+CESS+Cg+CBias
(1)
式中:CRE——可再生能源的运维成本;
CMT——火电机组的燃料成本与爬坡成本;
CIL——可中断负荷调用成本;
CEV——电动汽车充电站调度成本;
CESS——调度储能向储能聚合商支付的费用;
Cg——向大电网购电的成本;
CBias——微电网偏差考核费用。
其中,
(2)
(pu·ΔPU,t+pd·ΔPD,t)
(3)
(4)
(5)
(6)
(7)
(8)
式中:M1、M2——风电机组和光伏机组的数量;
PWTi,t、PEVi,t——t时段风电与光伏的出力大小;
pwto、pevo——风电与光伏机组的运维成本;
Δt——调度时间间隔;
a、b、c——火电机组的发电成本系数;
PMT,t——火电机组t时段出力大小;
ΔPU,t、ΔPD,t——火电机组t时段上、下爬坡电量;
pu、pd——火电机组上、下爬坡单位功率的费用;
PIL,t——可中断负荷中断的功率;
pIL——可中断负荷调度的单位费用,与调度功率之间的关系;
L——电动汽车充电站可调度电动汽车数量;
PEVi——第i个电动汽车充电桩的充电功率;
pEVi,t——t时段调度电动汽车用户参与调度费用;
β(pEVi,t)——电动汽车充电站响应调度的概率与补贴成本的关系[17];
T——总调度时长;
Pcha,t、Pdis,t——微电网t时段向储能聚合商购买的充放电电量;
ηcha、ηdis——储能充放电的充放电效率;
pESS——储能聚合商提供储能的服务费用;
k1——微电网购买服务的提价比例;
SESS——微电网安装的储能容量;
pgroup——储能聚合商整合储能单位容量费用;
Pb,t、Ps,t——微电网购售电量;
pb,t、ps,t——微电网购售电价格;
Plim——微电网偏差考核限值;
pBias——微电网偏差考核惩罚费用,与微电网偏差考核电量关系。
pIL,t=αPIL,t+β
(9)
(10)
式中:α、β——可中断负荷的价格系数。
(11)
1.2 微电网运行约束
针对微电网的优化运行模型,需要满足以下的约束。
(1)功率平衡约束为
PMT,t+Pdis,t-Pcha,t+Pb,t-Ps,t
(12)
(13)
(2)火电机组约束为
(14)
式中: ΔPUmax、ΔPDmax——火电机组的上爬坡与下爬坡限值;
PMTmin、PMTmax——火电机组出力的上下限。
(3)可中断负荷约束为
(15)
式中:PIL,max——可中断最大负荷功率;
QIL,max——周期内最大可中断负荷电量。
2 储能聚合商优化模型
储能聚合商通过向微电网支付费用获取各个微电网的储能使用权,通过向各个微电网提供储能服务获得服务费用与充分利用各个微电网调度的互补性,从而获取经济效益。当储能资源的需求小时,储能聚合商可以通过降低储能调用服务费用来吸引微电网,当储能资源需求较大时,微电网通过提高储能服务费用比例从而优先使用储能。
2.1 储能聚合商优化目标
本文中储能聚合商的运行经济性主要包括向各微电网购买储能使用权的成本、向各微电网提供储能的服务费用以及储能充放电产生的电能损耗成本。优化目标函数为储能聚合商运行成本Fesg,即
Fesg=Clease+CGloss-CIloss-Cser
(16)
式中:CGloss——储能聚合商实际调度产生充放电损耗成本;
Clease——储能聚合商向各微电网租赁的成本;
CIloss——各个微电网调度所支付充放电损耗成本;
Cser——各微电网调用储能所支付服务费用。
其中,
(17)
(18)
(19)
pgroup·(1+k2)·(1+k3)
(20)
式中:N——参与调度的微电网数量;
k2——储能聚合商的服务费用在租赁费用基础上提价的比例;
k3——储能聚合商基于微电网调度需求给出的调度折扣或提价比例。
2.2 储能全寿命周期成本
各微电网将储能按照配置储能的全寿命周期成本均摊到每一个调度时刻的费用折合作为租赁费用,从而减少微电网配置储能高昂成本带来财政压力。储能的全寿命周期成本主要由储能初始投资成本、电池更换成本、检修成本以及期末退役成本四个部分组成,计算公式为
CLCC=
(21)
式中:CesI——储能初次投资成本;
Cre——储能电池更换成本;
CesM.j——储能第j年的检修成本;
CesCD——储能的期末退役成本;
i——贴现率;
N——储能电站的寿命年限。
其中,
CesI=(ces+cel)Ses
(22)
(23)
CesM=λCesI
(24)
CesD=CesSC+CesSV=(μ1+μ2)CesI
(25)
式中:ces——储能电池的单位容量成本;
cel——电池外配置的单位容量成本;
Ses——储能电站的容量;
α——电池成本逐年下降比例;
L——储能电池的寿命周期;
ic——行业基准收益率;
λ——年维护成本与初始投资成本的比例系数;
CesSC——储能的设备残值;
CesSV——储能的报废成本;
μ1——储能设备残值的比例系数;
μ2——储能报废成本的比例系数。
2.3 储能运行约束
储能系统运行所需要满足的约束包括荷电状态约束、最大充放电功率约束。
(1)荷电状态约束为
(26)
(27)
(2)充放电功率约束为
(28)
(29)
式中:Et——储能系统t时段蓄电量;
EN——储能蓄电池的额定容量;
γmax、γmin——储能荷电状态上限、下限;

3 多微电网博弈优化运行策略
厘清多微电网系统中各种微源、负荷的拓扑以及同储能聚合商关系。多微电网系统与储能聚合商关系示意图如图1所示。

图1 多微电网系统与储能聚合商关系示意图
储能聚合商向各个微电网租赁储能的使用权,将储能资源统一调度,微电网可以节省不调度储能期间的储能寿命周期成本,从而提高微电网的运行效益;储能聚合商则可以利用不同微电网之间调度的互补性,避免不必要的储能调度功率,从而提高储能聚合商的收益。
文献[18]中提出的博弈机制基于配电网运营商作为先动方,优化配电网、微电网以及负荷聚合商等利益主体的运行策略,但不可避免会偏袒先动方,无法保证各主体的博弈公平性。基于此,为了保障各个微电网的博弈公平性,优化调度过程中双方的动作不存在先后,多微电网与储能聚合商的博弈优化状态动作图如图2所示。

图2 多微电网与储能聚合商的博弈优化状态动作图
4 自适应多智能体强化学习
本文中多微电网与储能聚合商多方博弈问题涉及多主体序贯决策问题,经典优化算法以及传统智能算法求解容易出现求解该非线性、动作离散的问题时容易陷入局部最优甚至无法找寻到最优解。基于此,借鉴文献[19-20]中多智能体与强化学习相结合的方法,来求解多主体博弈问题。在这一基础上,引入KL散度对比智能体学习经验与Nash均衡解,优化各个智能体的学习率,提高优质学习经验的学习率,并减小劣质学习率的影响,从而提升该算法的收敛性与收敛结果。
4.1 自适应学习率
在概率论或信息论中,KL散度又称相对熵,是描述两种概率分布差异的一种方法。机器学习领域内大多是用来度量两个函数或两种概率分布相似程度或者相近程度。如果两个分布越接近,KL散度越小;如果两个分布越远,则KL散度就越大。基于此,本文提出采用KL散度对比智能体的历史学习经验与纳什均衡策略分布,根据二者分布远近优化各智能体的学习率,强化优质学习经验。其中,自适应学习率公式为
(30)
式中:αi,t——第i个智能体t时段的学习率;
Pi,t——第i个智能体t时段历史经验的概率分布;
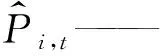

距离。
4.2 多智能体强化学习
多智能体强化学习是多智能体纳什均衡策略与强化学习算法的结合,其中,Nash均衡即当博弈中其他智能体的策略均给定时,则智能体无法通过改变自身策略收获更优的回报,其表达形式为
(31)
式中:νi——第i个智能体在状态St下的收益;
π*——纳什均衡策略;
n——参与博弈的智能体个数。
强化学习是智能体经历不同状态下尝试不同动作,通过状态动作对值函数对智能体行为策略的优劣进行评估,从而获得累积奖励最大化的最优策略,根据环境的回报提升智能体对不同环境的决策能力。其中,Q学习是一种常用的强化学习算法,递归公式为
(32)
式中:α——学习率;
γ——折扣率;
r——在执行动作的回报;
Q(s,a)t——第t次迭代中在状态s下执行动作a的Q值;
s′——动作后的状态;
maxQ(s′,a′)t——第t次迭代中状态s′下的最优策略;
A——智能体的动作空间。
在多智能体博弈系统中,采用纳什均衡策略与强化学习结合后的Nash-Q算法[21]对各个智能体的Q值进行更新,其迭代公式为
Qi(s,a1,a2…,aN)t+1=(1-αi,t)Qi(s,a1,a2…,an)t+
(33)
式中:Qi(s,a1,a2…,an)t——t时段状态s下智能体动作组合为a1,a2…,an的Q值;
αi,t——第i个智能体的自适应学习率;
NashQi(s′)t——各个智能体在t时段状态s′的一个纳什均衡解。
(34)
4.3 模型求解
为了能够判断各个智能体训练结果是否收敛,本文采用各个智能体迭代前后的Q值之差的二范数归一化结果,作为算法收敛的判断标准。
(35)
式中:Qi,t——第i个智能体第t次循环得到的Q值;
σ——较小的正数;
N+1——智能体总个数,涵盖所有参与博弈的微电网与储能聚合商。
共享储能模式下多微电网博弈优化模型的求解流程如图3所示。

图3 共享储能模式下多微电网博弈优化模型的求解流程
5 算例分析
5.1 算例数据
本文以3个地域邻近的微电网某典型日运行数据为例分析。各个微电网中可再生能源出力曲线与负荷曲线如图4所示。考虑可再生能源消纳政策,本文中不对可再生能源进行限电。
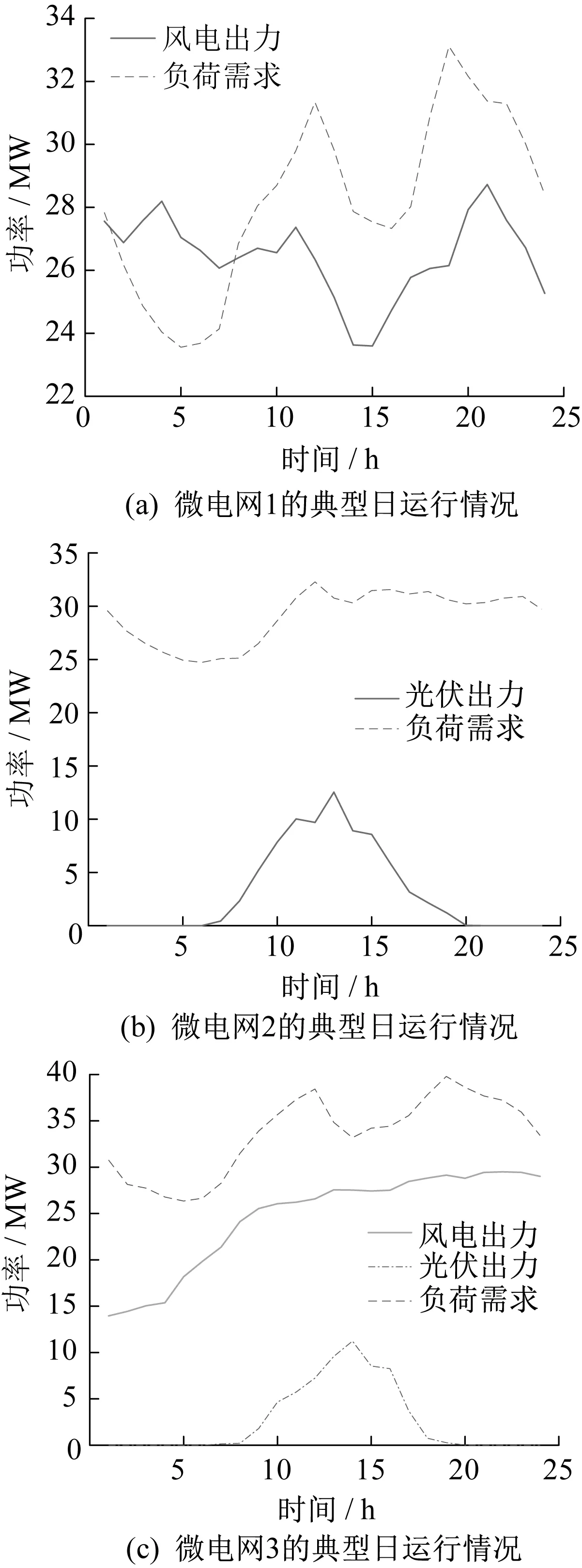
图4 各个微电网中可再生能源出力曲线与负荷曲线
3个微电网中火电机组燃料成本系数分别为0.002 41、27.62、1 139,上爬坡成本50元/MW,下爬坡成本10元/MW。可中断负荷的参数如表1所示;各主体租赁储能的价格提价与折扣比例如表2所示;储能荷电状态上限、下限分别为0.1、0.9,充、放电效率分别为93.5%和94.4%;电价峰时段为11∶00~15∶00、19∶00~21∶00,谷时段为24∶00~次日6∶00,其余时段为平时段,购、售电价格分别为0.17 元/kWh、0.49 元/kWh、0.83元/kWh与0.13元/kWh、0.38元/kWh、0.65元/kWh。参考目前各省份的可再生能源储能配置政策,一般为可再生能源装机容量的10%~15%,本文中3个微电网的储能配置分别为3 MW/3 MWh、2 MW/2 MWh、5 MW/5 MWh。
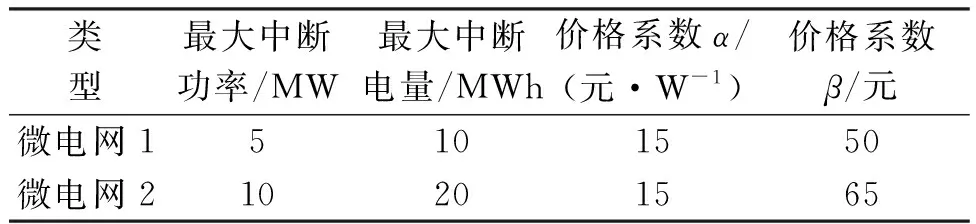
表1 可中断负荷参数

表2 各主体租赁储能的价格提价与折扣比例
5.2 结果对比分析
各微电网独立优化结果如表3所示;共享储能模式下各微电网博弈优化结果如表4所示。由表3与表4的经济性对比可以看出,微电网在共享储能模式下可以显著降低其运行成本。不同优化调度模式下储能调度功率如图5所示。
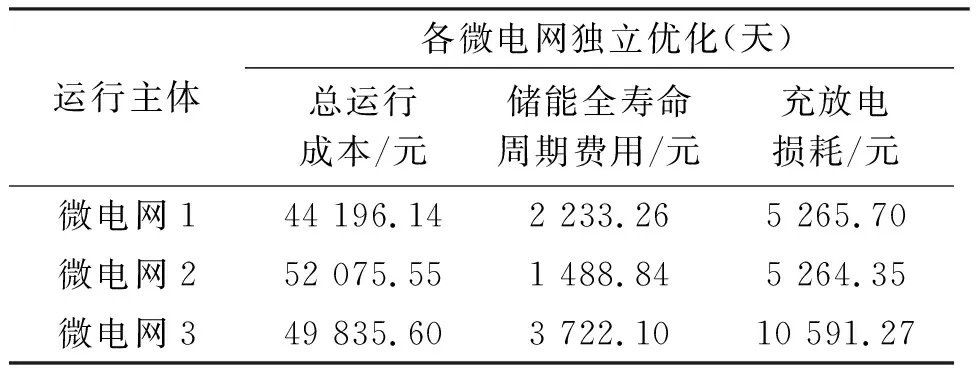
表3 各微电网独立优化结果
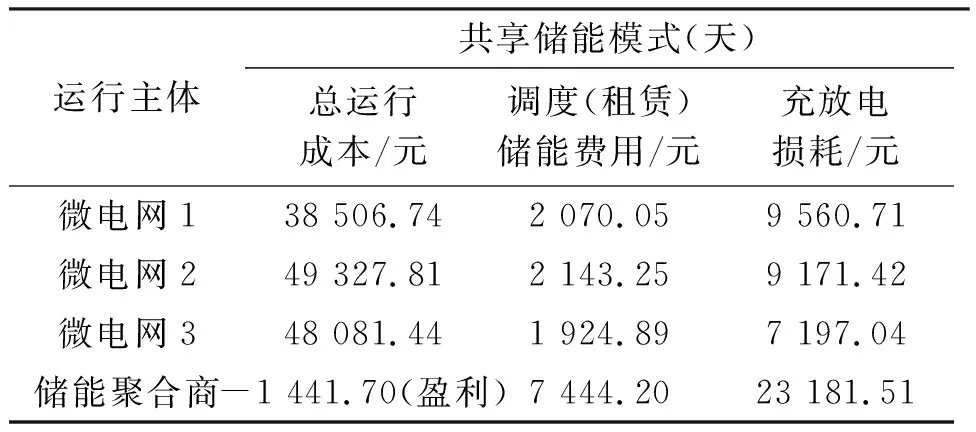
表4 共享储能模式下各微电网博弈优化结果
由图5可以看出:

图5 不同优化调度模式下储能调度功率
(1)微电网3的租赁储能成本低于储能全寿命周期成本,即通过共享储能的模式,微电网3通过向储能聚合商租赁自己的储能设施提高其经济性,运行成本下降了3.52%。
(2)微电网1与微电网2在储能配置容量较小情况下,通过向储能聚合商购买储能服务,减小微电网出力偏差考核与峰时购电等费用,运行成本分别降低了12.87%与5.28%。
(3)储能聚合商租赁储能的费用较提供储能调度服务的费用高,但其通过合理调度不同微电网的储能调度需求,各微电网的调度需求从49 MW减少到29 MW,通过节省充放电的损耗费用盈利,日投资收益率为4.7%。
5.3 算法对比分析
为了验证本文中引入KL散度优化多智能体强化学习学习率的有效性,本节对比了是否引入KL散度优化智能体学习率的算法收敛曲线。算法收敛曲线对比如图6所示。
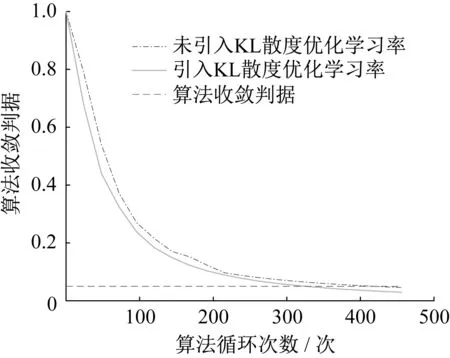
图6 算法收敛曲线对比
由图6可见,本文引入KL散度后的多智能体强化学习算法的收敛速度较快,收敛所需次数为360次,而未引入KL散度优化智能体学习率的多智能体强化学习算法则需要456次。二者循环单次所需时间分别为93.54 s与92.60 s,本文算法的收敛时间远低于改进前的算法,验证了本文算法的优越性。
6 结 语
本文以各微电网运行成本最小与储能聚合商效益最大作为多主体博弈的优化目标,全面考虑了可中断负荷、火电机组以及电动汽车充电站等诸多灵活性资源等因素对共享储能模式的影响,建立了储能聚合商对多微电网储能设备整合下多微电网博弈优化模型,采用全寿命周期成本建立共享储能系统的租赁成本模型,得出共享储能模式下各微电网的运行策略,并采用多智能体强化学习算法对各微电网与储能聚合商的运行策略进行优化,对比了微电网基于自身储能设施的优化运行经济性和共享储能模式下的经济性。主要结论如下:
(1)共享储能模式通过综合各微电网的储能调度需求,减少了40.82%的储能充放电功率,节省储能的充放电损耗费用,且随着调峰、调频市场的开放,还可以通过储能提供调峰、调频服务来获取额外的经济效益。
(2)共享储能模式通过租赁各微电网的储能设施,降低了微电网3典型日运行中32.04%的充放电损耗,避免了储能设施配置过度造成灵活性资源浪费。此外,微电网1与微电网2通过租赁储能降低了自身运行成本,避免了额外配置储能造成储能资源的浪费。
(3)共享储能模式下储能聚合商不需要对储能设施进行前期的大规模投资,日投资收益率达到4.7%,对于社会资本有着较好的吸引力。
(4)本文引入KL散度优化多智能体强化学习算法,提升算法的收敛速度,收敛所需时间缩短了20.25%,节省了计算成本。
