基于LSTM的燃煤电厂NOx排量软测量
2022-04-28潘红光裴嘉宝辛芳芳
潘红光,裴嘉宝,苏 涛,辛芳芳
(西安科技大学 电气与控制工程学院,陕西 西安 710054)
0 引 言
火力发电以煤电为主,燃煤电厂煤粉在燃烧过程中产生的有害气体会对大气环境造成污染。目前,燃煤电厂主要通过SCR(selective catalytic reduction,SCR)脱硝系统降低NOx排放量[1],锅炉燃烧工艺流程如图1所示。为有效应对NOx的排放,对其进行实时测量至关重要。NOx的排放量一般通过建立湍流模型[2]、气固流动模型[3]等方式进行测量。目前,NOx排放量一般采用硬件传感器或者分析仪,利用连续排放监测系统(continuous emissions monitoring system,CEMS)进行实时测量。然而,CEMS在线测量NOx排放量时,投资成本过高、计算速度慢、测量存在滞后性等缺点,难以满足烟气出口NOx排放量迅速、稳定的监测要求。对于复杂工业环境而言,在具体生产过程中受设备和技术因素的影响,往往导致有些关键变量测量误差较大甚至难以测量。除此之外,某些设备测量的结果时间上存在滞后性无法实时指导生产活动,这就很难对生产活动进行实时控制。软测量技术的发展正是为了解决这类质量指标的实时测量和控制问题。

图1 锅炉燃烧工艺流程Fig.1 Process flow chart of boiler combustion
软测量技术主要依据工业生产过程中可测的辅助变量来实时估计待测的目标变量[4]。软测量技术的基本过程如下:首先,通过对目标变量的分析,选择与目标变量密切相关的易测量;其次,通过数据采集和预处理,确定数据的有效性后建模;最后,对模型进行分析确定其是否满足实际生产需求。大量的文献表明,软测量技术具有实际运用价值。GONZAGA等采用基于人工神经网络(artificial neural network,ANN)的软测量方法对一个聚合过程的聚合物粘度进行估计,并将此估计结果成功应用于伺服和调节问题,并使得工业装置有效运行[5]。LI等提出一种利用灵敏度矩阵分析和核脊回归(kernel ridge regression,KRR)实现蒸馏成分在线软测量的组合软测量传感器,并在模拟精馏塔上的应用表明该方法的有效性[6]。毛清华等针对采煤机机截割载荷难以直接测量的问题,采用基于ELM神经网络的软测量方法建立采煤机机截割载荷软测量模型,结果表明软测量建模方法能够实现采煤机机截割载荷预测[7]。由以上文献研究和分析可知,软测量技术在不同领域的实际应用中,都取得相应的成果,充分体现它自身所具有的优势。
考虑到电站锅炉具有大惯性、大滞后、时变和不确定性的特点,且各参数之间相互耦合,各个过程难以使用准确的数学模型来表征;同时,机组运行过程积累了大量数据,因此研究基于数据驱动的建模方法有望获得有效的NOx排放量测量模型。近年来,研究人员提出很多方法用于分析锅炉能效问题。例如MA等利用径向基函数(radial basis function,RBF)神经网络建立1 000 MW超超临界机组模型来测量机组负荷、主蒸汽压力和中间点温度,获得很好的效果,具有很强的实际工程意义[8]。GU等提出一种自适应最小二乘支持向量机(adaptive least squares support vector machine,ALS-SVM)算法,对锅炉燃烧系统建模,结果表明该模型能够很好反映锅炉燃烧系统的时变特性[9]。李竞岌等利用小型鼓泡流化床实验台比拟循环流化床(circulating fluidized bed,CFB)锅炉密相区,在850 ℃床温和10%O2浓度下,进行单颗粒焦炭的燃烧实验,对不同床料粒度、制焦煤种、焦炭粒径和流化风速条件下焦炭氮向NOx的转化比例进行研究[10]。王科等在锅炉原始燃烧系统的基础上调整二次风配比并且引入燃尽风(separated over-fire air,SOFA),通过数值模拟的方法评估新型燃烧系统在不同SOFA风率和不同SOFA位置时的整体燃烧性能,结果表明SOFA参数对NOx排放和飞灰含碳量有影响[11]。这些文献从不同方面分析锅炉能效问题,说明研究基于数据驱动的NOx排放量测量的建模方法具有实际意义。
锅炉NOx排放量在数据上是一个非线性的时间序列,信息彼此间有着复杂的时间关联性。目前,广受关注的诸多深度学习方法,是一种能够模拟出人脑的神经结构的机器学习方法,可以有效处理此处的非线性问题[12]。BP神经网络和长短期记忆(long short term memory,LSTM)网络就是其中的一部分。BP神经网络是一种经典算法,它是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用较为广泛的神经网络。ZHOU等提出一种基于BP神经网络的自适应卡尔曼滤波算法,分析吸烟者和非吸烟者呼出CO和N2O的浓度[13]。TAO等提出一个结合BP神经网络和地质统计学来描述污染场地的土壤污染物情况的模型[14]。但BP神经网络泛化性较差,而LSTM神经网络考虑数据的时间特性,在时间序列预测方面有更好的表现[15]。MA等研究LSTM神经网络的架构,与动态神经网络的不同拓扑以及SVM等其他算法比较,表明LSTM在准确性和稳定性方面可以实现最佳短期交通预测性能[16]。由以上文献可知,LSTM对时序性数据处理效果较好。
综上所述,基于LSTM网络能够学习到数据间的长期依赖性[17-18],同时针对锅炉NOx浓度时间序列预测这一问题,笔者提出一种基于LSTM神经网络的软测量方法对NOx排放量进行实时测量。首先,对NOx产生机理分析,并在实际生产数据集上初步选取与NOx排放量紧密相关的20个辅助变量;其次,在数据预处理后,利用灰色关联度分析精选出15个辅助变量;最后,通过训练集和测试集对LSTM模型进行训练和测试,并将LSTM模型与BP神经网络模型和SVM模型的软测量结果比较发现,LSTM模型的预测准确度更高,泛化能力更强。
1 LSTM神经网络
1997年,HOCHREITER等提出LSTM神经网络,目的是解决循环神经网络(recurrent neural network,RNN)梯度消失问题[19]。
RNN结构如图2所示,图中,Di(i=0,1,…,t)为时间i的输入;ui(i=0,1,…,n)为输出;中间部分E是隐藏层的信息流。但是,随着时间序列的不断增长,RNN将出现梯度消失问题,而LSTM神经网络的提出,成功解决此类问题。
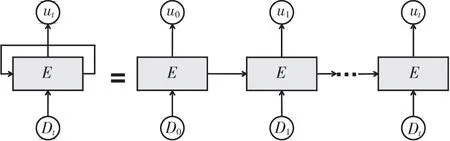
图2 RNN网络结构Fig.2 Network structure of RNN
LSTM神经网络是一种特殊的RNN,可有效解决传统RNN梯度消失或梯度爆炸现象[20-21]。LSTM将每一层神经元加入了“门控”结构,使得部分误差在传播过程中可以直接通过“门”,而不用归因于当前神经元。因此,误差可以直接传播到下一层,梯度无论传播多远都不会出现梯度消失问题。在RNN隐藏层中,LSTM加入输入门(Input Gate),输出门(Output Gate),遗忘门(Forget Gate)和一个内部单元(Cell),如图3所示。

图3 LSTM单元内部模型Fig.3 Internal model of LSTM unit
输入门控制着新的输入信息进入记忆单元的强度,即决定着多少新记忆和老记忆进行合并。
(1)
(2)

遗忘门决定细胞状态中丢弃什么信息。
(3)
(4)
Cell的状态更新如下。
(5)
(6)
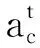
输出门控制长期记忆对当前输出的影响,并确定输出值。
(7)
(8)
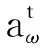
最终通过以上3种门状态输出新的细胞状态。
(9)
式中h(·)为激活函数,这里h选择tanh函数。
在式(1)~式(9)中带h的权重矩阵(ωh*或ω*h)均代表一种泛指,因为LSTM的一个重要特点是其灵活性,即Cell之间的互联和隐含层之间互联,可根据具体情况选择连接与否。
文中采用均方误差(MSE)作为误差函数用于神经网络的误差反向传播学习。
(10)
式中yi,pi分别为第i组样本真实输出和预测值。
2 NOx排量软测量
2.1 数据采集与辅助变量初选
实验数据来自陕西省榆林某电厂实际生产数据,数据内容为实测样本,数据采集点是2019年1月1日 00∶00至6月9日2∶00,采样间隔为1 h,共3 800个采样点数据。
通常燃煤电厂锅炉燃烧产生的NOx主要分为3大类,分别为燃料型NOx、热力型NOx与快速型NOx。燃料型NOx在3种污染物中比例最大,它是煤质的直接燃烧产生的污染物;热力型NOx在3种污染物中比例较小,它是送风机送入的氮元素在锅炉中被氧化产生的污染物;快速型NOx在3种污染物中比例最小,它是煤质中的碳元素与空气中的氮元素发生瞬时反应产生的污染物。通过对NOx生成原因分析,初步选取总给煤量、锅炉总风量、炉膛出口温度等3 800×20组变量(见表1变量1~20),其中脱硝出口NOx排放量为目标变量。

表1 辅助变量Table 1 Auxiliary variables
其中,NOx国家的排放标准主要依据国家2014年发布的并且要求2016年7月开始执行的国家锅炉大气污染物排放标准,具体为:
1)燃气锅炉:在用锅炉 400 mg/L、新建燃气锅炉 200 mg/L、重点地区 150 mg/L;
2)燃煤锅炉:在用锅炉 400 mg/L、新建燃气锅炉 300 mg/L、重点地区 200 mg/L;
3)燃油锅炉:在用锅炉 400 mg/L、新建燃气锅炉 250 mg/L、重点地区 150 mg/L。
2.2 数据预处理
考虑到工业环境复杂性,前述实测数据使用前需预处理。数据预处理包括随机误差、粗大误差的处理及数据变换。粗大误差一般由于传感器失灵、设备异常等造成,一般情况下,粗大误差出现概率较低,一旦出现会严重影响数据质量。随机误差主要由于测量信号的干扰及操作过程的随机波动成。
2.2.1 粗大误差处理
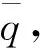
(11)
若样本qk的偏差vk(1≤k≤n)满足|vk|>3σ,则该样本数据为粗大误差数据,应予剔除。
2.2.2 随机误差处理
采用数据滤波中的滑动平均值法处理数据的随机误差。具体过程为:定义滑动时间窗口长度为k,设第i时刻参数的测量值为qi,用i到i+k时刻窗口中样本的平均值代替qi的观测值,即可消除随机误差。其过程描述如下
(12)
2.2.3 归一化与反归一化处理
各个数据之间的数量级差别过大,需要对数据进行归一化处理
(13)
式中Qi为归一化处理后的数据。为了返回原始量纲,须进行反归一化处理
qi=Qi(qmax-qmin)+qmin
(14)
2.3 辅助变量精选
辅助变量精选可将数据维数控制在恰当范围内;辅助变量太多会影响模型灵活性和时效性;反之,又难以充分输入参数的特征信息,影响模型适用性和准确性。考虑到表1中变量1~20之间具有不同程度关联,因此,采用灰色关联度分析法量化变量间的关联度,以精选辅助变量。灰色关联分析法主要依据序列曲线几何形状的相似程度来判断其联系是否紧密:曲线越接近,相应序列间的关联度越大;反之,越小。
采用灰色关联度获得各辅助变量关联度,见表1。设定关联度阈值为0.90[23-24]。据此阈值,精选2号给煤机密封风调门反馈、1号机组烟囱入口烟气O2浓度、左侧炉膛出口温度、右侧炉膛出口温度等关联度大于 0.90的15个辅助变量。因此,最终有效数据规模为3 800×15。
2.4 软测量建模
软测量技术的主要思想是:采用便于测量的变量来实时估计待测的目标变量。采用2号给煤机密封风调门反馈、1号机组烟囱入口烟气O2浓度等15个辅助变量,利用LSTM算法进行软测量建模估计目标变量脱硝出口NOx排放量,具体过程如下。
1)根据燃煤电厂的理论和技术收集脱硝出口NOx排放量和相关数据,并构建数据集。
2)使用(11)消除粗大误差,使用(12)消除随机误差,并使用(13)~(14)标准化数据。
3)运用灰色关联度对数据进行降维处理,以实现辅助变量的精选,并将数据集划分为训练集和测试集。
4)建立深度学习模型并初始化LSTM神经网络相关参数。
5)训练:在正向传播中,使用(1)~(9)获得预测输出;在反向传播中,使用梯度下降法来计算每个权重的梯度。之后经过迭代和修改权重,使损失函数最小化,并输出最优模型。
6)测试:公式(10)用于计算测试集的评估指数。
7)如果精度符合要求,则输出最终的LSTM神经网络模型。否则,返回步骤 4)调试LSTM神经网络参数。
3 仿真实验
实验中软件环境为:Python的框架——PyTorch 0.3.1,Python编辑环境为PyCharm,操作系统为Win7(64位);硬件配置为:内存DDRIII 12G(8G+4G),CPU为 AMD A4-Series A4-5000。
3.1 场景及参数设计
一般来说,数据规模会对数据驱动方法的结果产生较大影响[25]。考虑到很多场景下大规模数据获取存在困难,在仿真部分对小数据量(场景 1)和大数据量(场景2)分别进行仿真[26-27]。为便于比较,测试集数据均选为240组(2019年5月 30日 2∶00至6月9日2∶00)。场景1训练集为480组(2019年5月10日1∶00至5月30日1∶00);场景2训练集为3 560组(除去240组测试数据后的剩余数据)。
与此同时,为比较文中所提方法的有效性,此部分还对基于BP神经网络和SVM的2种方法进行仿真,并分别作了比较。根据上文选定的模型结构,基于LSTM神经网络的软测量模型参数见表2。BP神经网络具体建模方法可参考[26],具体参数见表2。对于SVM建模方法可参考[9],其主要参数为最佳惩罚系数μ和径向基函数的宽度ψ,其中,场景1下训练后的参数ψ=11.313 7,ψ=0.022 1,场景2下训练后的参数μ=2.828 4,ψ=0.250 0。
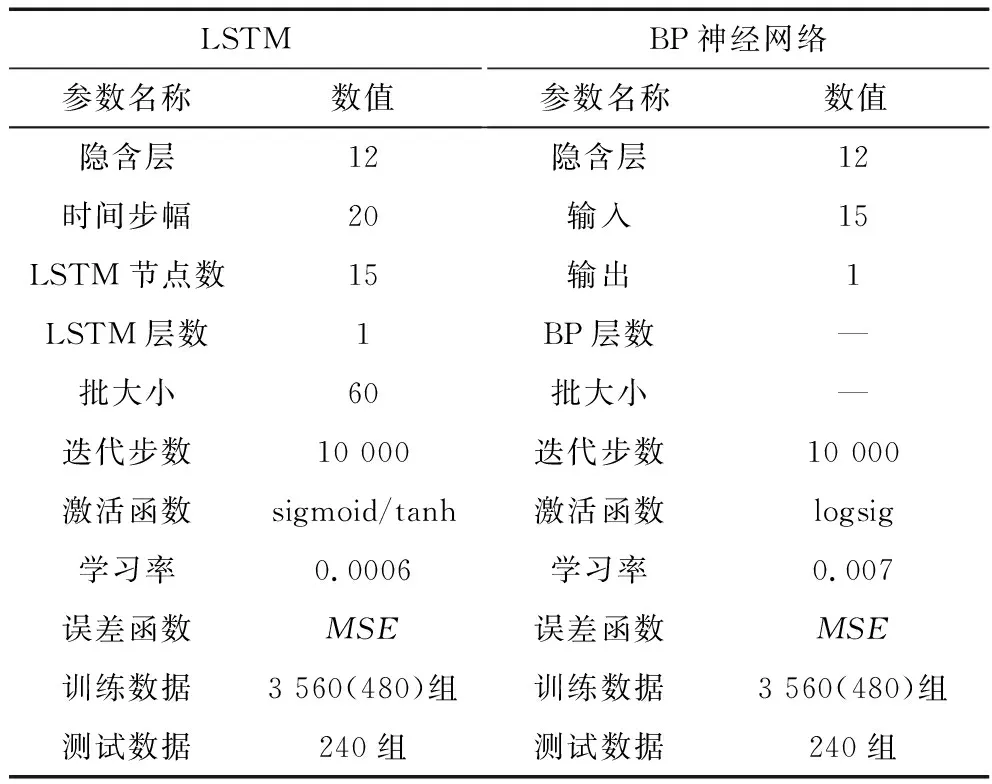
表2 网络模型参数Table 2 Network model parameters
3.2 场景1仿真结果
图4展示LSTM训练过程的均方误差(MSE)与迭代次数的关系:随着迭代次数的增加,训练误差逐渐缩小。这一规律在场景1(红色实心圆)和场景2(蓝色实心圆)中基本一致;只是在场景2(大数据量)下,均方误差下降速度更快。说明对于LSTM神经网络模型而言,训练集规模越大,训练速度越快。
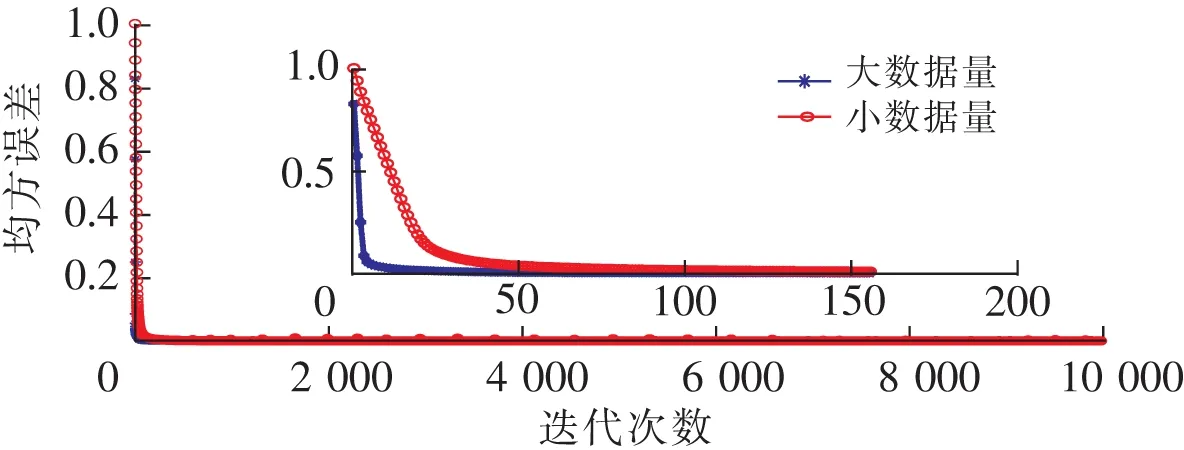
图4 LSTM训练误差Fig.4 LSTM training errors
图5~7给出场景1下3种方法的预测结果。整体来看,此种场景下基于SVM模型的预测精度最优。为进一步量化各方法的预测效果,表3分别从均方误差(MSE)、均方相关系数(r2)两方面对预测效果进行展示。其中,MSE反应的是预测值与真实值的偏离程度,MSE越小,说明模型精确度越高;r2反应2个变量变化时的相似程度,该系数越高表示预测值与真实值越接近;二者相互结合,综合反应模型的优劣。
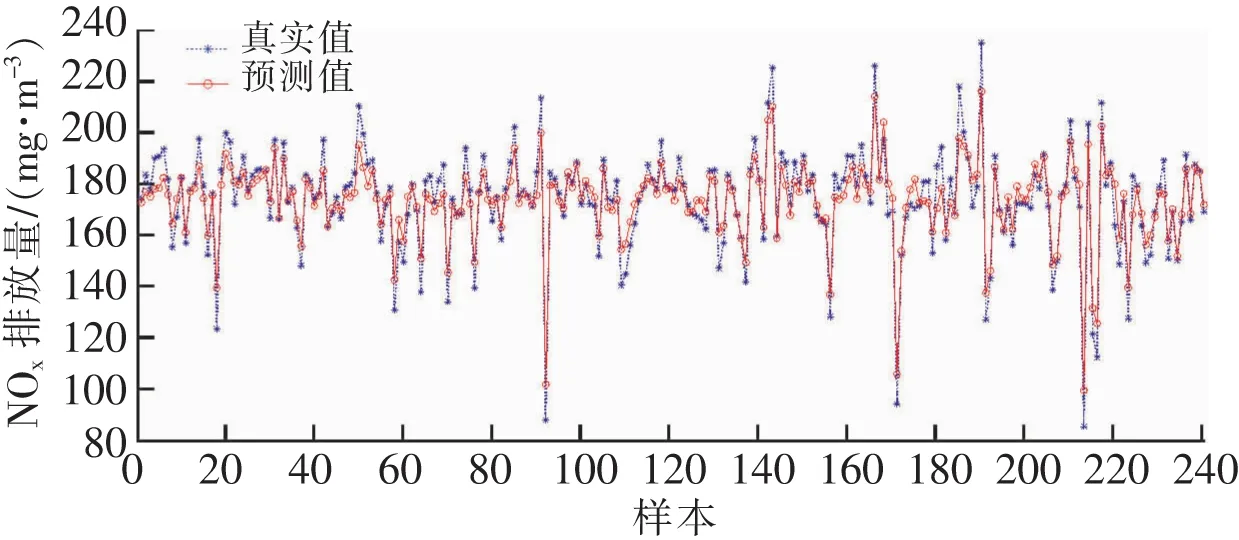
图5 场景1基于LSTM的模型预测结果Fig.5 Forecast results of LSTM based model in Case 1

图6 场景1基于BP的模型预测结果Fig.6 Forecast results of BP based model in Case 1

图7 场景1基于SVM的模型预测结果Fig.7 Forecast results of SVM based model in Case 1
据表3,场景1下SVM的MSE比BP和LSTM分别低0.000 3和0.002 0;SVM的r2比BP和LSTM分别高0.014 0和0.026 8。也即,基于SVM的模型2项指标均优于其他2种模型。该结果说明,基于SVM的模型在小数据量的情况下其泛化能力更强,预测结果更好,适用于小数据量场景[9]。
3.3 场景2仿真结果
图8~10给出3种方法在场景2下的预测结果。从整体看,场景2下基于LSTM模型的预测精度最优。由表3可知,场景2下LSTM的MSE比BP和SVM分别低0.000 2和 0.000 5;LSTM的r2比BP和SVM分别高0.020 6和0.065 9。即,基于LSTM的模型2项指标均优于其他2种模型。该结果说明,基于LSTM的模型在大数据量情况下泛化能力更强,预测结果更好,适用于大数据量场景[9]。
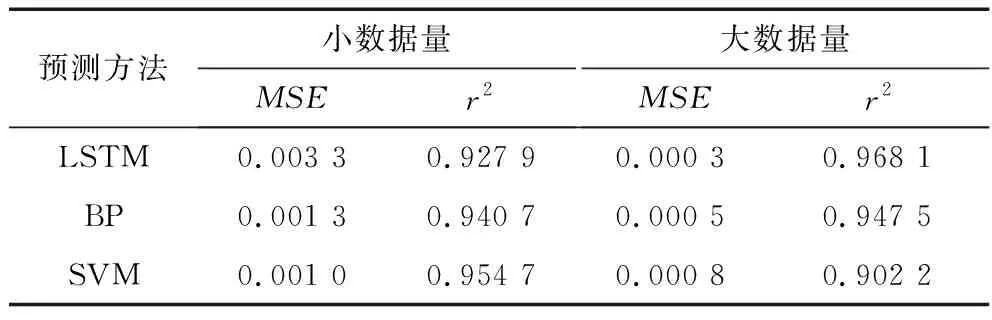
表3 3种方法结果比较Table 3 Result comparison of three methods

图8 场景2基于LSTM的模型预测结果Fig.8 Forecast results of LSTM based model in Case 2

图9 场景2基于BP的模型预测结果Fig.9 Forecast results of BP based model in Case 2
结合表3及图5~图10,可以得出如下结论:在大数据量的基础上,基于LSTM的模型较基于BP和SVM的模型能够学习到数据间的长期依赖性,同时对时间序列有强化记忆能力的特点[27];其具体原因在于,LSTM加入“门控”结构替换原RNN网络结构中的隐含层细胞,通过“门控”结构将长期记忆与短时记忆结合,使得部分信息在传递过程中可以直接通过“门”,而直接越过当前神经元,可以有效地处理长期依赖的动态相关问题,在一定程度上弥补RNN网络“梯度消失”的问题;LSTM特殊的“门控”结构,使其在处理时序问题上的性能优于RNN网络。同时表明,在当前数字化日益普及、大量数据存在的情况,基于LSTM模型的NOx排放量等方面的预测完全可行。所提方法在降低企业测量仪表投入、减少维护成本等方面具有很好的效果。
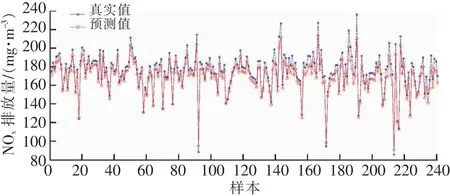
图10 场景2基于SVM的模型预测结果Fig.10 Forecast results of SVM based model in Case 2
4 结 论
1)针对燃煤电厂NOx浓度排放量的测量这一复杂的非线性动态系统,提出基于LSTM的NOx排放量软测量方法,该方法主要是分析与NOx排放量紧密相关的变量,通过构建NOx排放量软测量模型实现NOx排放量的预测。
2)LSTM特殊的“门控”机制,使得LSTM在处理时序问题上更具优势;燃煤电厂在生产过程中的历史数据的关联性及时序特征;基于LSTM的NOx排放量软测量主要是结合LSTM的优势以及燃煤电厂生产过程历史数据的特性来实现NOx排放量的预测。
3)基于LSTM的NOx排放量软测量主要选择均方误差和均方相关系数作为评价模型预测性能的标准。从仿真实验结果来看,LSTM神经网络的软测量方法预测结果优于BP神经网络和SVM模型。
4)该方法在NOx排放量的预测方面效果不错,但是存在一定的不足,比如在小数据量的情况下,预测性能会有所下降,后续研究需要根据不同的应用场景、数据集的不同、领域的不同构建出符合数据标准的模型。
