蚁群优化算法的无人机室内航迹规划
2022-04-28马肇祥朱庆伟屈乾龙
马肇祥,朱庆伟,张 俊,屈乾龙
(西安科技大学 测绘科学与技术学院,陕西 西安 710054)
0 引 言
无人机因其操作简便、机动性能好等特点,已经被广泛应用于各个领域。将无人机用于执行室内灾害救援任务时,可以减少救援人员的安全风险,提高救援工作效率。航迹规划是无人机完成自主飞行的关键技术之一,在室内救援时,寻找一条安全、可靠的飞行航迹是保证救援任务能否完成的关键。无人机室内飞行面临的挑战是室内空间狭小、障碍物较多,高度有限,使无人机飞行受到一定条件的限制。在室内,由于环境信息是未知的,航迹规划要满足避障要求,规划一条合理路径。
目前,各国学者已提出许多种无人机航迹规划算法。常用到的算法有:可视图法、D*算法[1]、A*算法[2]、人工势场法[3]、神经网络算法[4]、快速搜索随机树(RRT)算法[5]、遗传算法[6]、粒子群算法[7]、蚁群算法[8-10]、模拟退火算法[11]、强化学习算法[12]等。其中,蚁群算法在求解较优航迹方面较其他算法具有显著优势。对蚁群算法进行改进应用于航迹规划的研究,国内外学者作了大量的研究工作。陈侠等提出的算法为使蚁群算法能更好适用于无人机三维航迹规划,对算法存在的收敛速度慢、易陷入局部最优的问题,进行了相应改进,将三维航迹规划分解成二维平面规划和高度规划2部分,运用几何优化法增强蚁群的引导方向性,根据无人机航迹点与障碍物之间的距离,对飞行高度进调整,利用自适应变化阈值参数法提高了蚁群在全局中的搜索能力,从而达到求解多样性的效果[13]。针对蚁群算法所含有的空间复杂性高、收敛速度慢的缺陷,魏江等提出的算法改进部分对局部搜索策略和初始信息素调节因子进行优化,在启发函数中加入路径偏移因子,有效降低空间搜索复杂性,提高了路径规划效率[14]。徐玉琼等针对传统蚁群算法在路径规划中对鲁棒性缺乏的问题,提出改进自适应蚁群算法,在概率转移规则中引入加权因子,以提高算法收敛速度,并按解的分布状况适应性地对信息素进行更新,同时在步长选择策略中选择最优步长,增强算法全局搜寻能力,从而提高机器人路径规划效率[15]。李宪强等将人工势场法与蚁群算法融合组成新的融合算法。由于蚁群算法易陷入局部最优,引入人工势场法对初始信息素进行分配。并且引入势场引导函数对蚁群算法的状态转移函数进行相应改进,从而避免算法因忽视周围障碍物信息而陷入长时间进行路径选择的问题[16]。这些研究都将蚁群算法用到具体的环境[17-22],取得良好的效果,然而,对于文中研究的室内无人机航迹规划,并不适用。因为这些算法应用于室外环境,且算法规划速度较慢,搜索时间较长,难以满足室内灾害救援及其他室内飞行任务的要求。
由于室内环境分布着大量障碍物,且障碍物分布不均以及其高度、形状、大小都各不相同[23-25]。而无人机在室内进行搜救或者自主导航时,室内环境信息并不能保证都了解。笔者结合室内环境特点及蚁群算法存在的缺陷,对空间做离散化处理,降低其空间复杂度。针对搜索初期,因信息素的缺乏,会导致搜索的盲目性,采用信息素调节因子,同时根据算法存在收敛速度慢和易陷入局部最优的缺点,设计启发概率,并改进信息素更新规则和采用动态信息素挥发策略。最后,通过实验测试对改进后的算法性能进行验证和分析。
1 空间离散化
室内环境中随机分布着很多障碍物,且空间环境处于连续状态。当发生灾害时,室内障碍物和突发的各种不确定因素给航迹规划带来巨大挑战。因此,对室内三维空间环境进行离散化处理,则在航迹规划时可以直接获得空间节点集。即在空间节点集中找到组成路径规划的总成本代价最小的节点。
设每个节点qindex,代表无人机的一个三维坐标(xindex,yindex,zindex),设所有处于离散状态空间节点的集合为q
q={q1,q2,…,qn=(xindex,yindex,zindex)}
(1)
对于无人机从起始点到目标点飞过的路径节点构成的集合用K表示
K={K1,K2,…,Kn}
(2)
(3)
2 改进的蚁群算法
在基本蚁群算法中,概率选择并不能总是保证最优解,有时在优化的早期,算法会进行盲目搜索、易陷入局部最优,而且由于启发式搜索的局限性,导致算法收敛速度很慢,为提高基本蚁群算法的性能并克服其缺点,做出以下改进:改进初始信息素调节因子,有效增强蚁群算法的搜索方向性;设计启发概率并改进状态转移概率函数,从而扩展蚁群搜索视野和提高可见性精度;对信息素更新规则进行改进和增加信息素挥发率的动态调整策略,有效提升算法的收敛速度、扩大搜索空间。
2.1 初始信息素的改进
由于基本蚁群算法的初始信息素均匀分布于空间中,因此在算法搜索初期,蚂蚁选择任意节点位置的概率都相同,从而出现蚁群盲目搜索的现象,同时也耗费大量的时间。
为避免蚂蚁在算法搜索初期的盲目性,在起始点和目标点连线的区域中,通过起始点到当前节点的距离和待选节点到目标点距离的变化量来影响初始信息素。基本蚁群算法的初始信息素是一个固定常数值,改进蚁群算法通过确定起始点、当前节点、待选节点以及且标点之间的距离,使蚁群尽可能沿着起始点和目标点连线的附近进行路径搜索,从而缩小路径搜索范围,因此对初始信息素调节因子进行了如下设计。
(4)
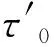
通过对上述信息素调节因子的设计使改进算法达到增强蚁群搜索方向性的效果。
2.2 启发概率
ST是组合运算,启发概率设计了让蚂蚁更容易选择最好的下一个空间网格(将室内空间按单位长度等分为大小相等的多个空间网格),所选网格必须是一个可行的网格,有多个可行通道抵达目标。这个概率取决于网格周围障碍物的数量。因此,空间网格周围的障碍物越少,概率就越大,网格就越有吸引力。需要做以下组合。
在三维空间中,无人机在搜索时,有27个搜索方向,去掉无人机本身的所占据的位置,因此剩于26个方向,即N(26,Mobs),它表示围绕一个确定的网格j,其周围障碍物可能分布的数量,即表征一个可行网格节点周围有多少障碍物,且障碍物数量为[0,26],如图1所示。
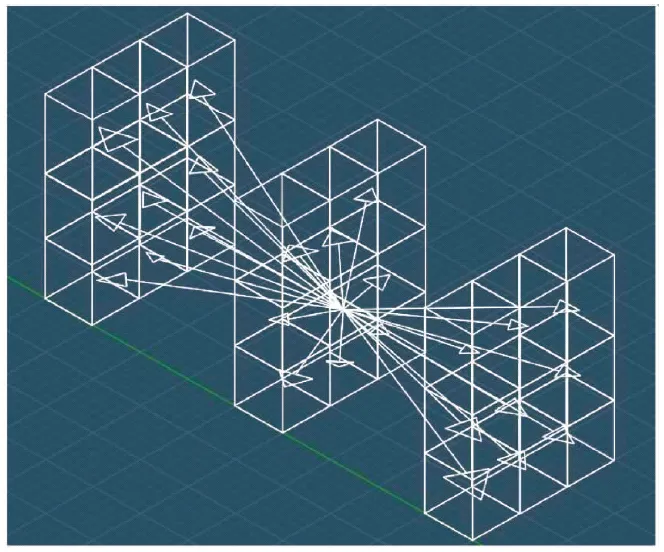
图1 旋翼无人机空间搜索示意Fig.1 Schematic diagram of rotor drone space search
它的计算方法如下
(5)
式中N(26-Mobs-1,1)为蚂蚁k可以离开网格节点j的通道数量,即在离开节点j后,能够选择的下一可行节点的数量。它的计算方法如下
(6)
其中N(a,e)=a!/(a-e)!e!为一个数学组合;Mobs为网格j周围障碍物的数量,26是障碍物的最大数量和!表示阶数。在通道数量计算中,必须取消蚂蚁k将要选择到达网格节点j的路径通道。
使空间网格i中的蚂蚁k更容易被网格j吸引的ST由下式定义
(7)
由此产生的转移规则按下式进行定义
(8)
式中j∈allowedk。
2.3 改进信息素更新规则
信息素的数量是选择经过最短路径上的最佳空间网格的必要因素之一,然而,它含有一定强度的劣质信息素,这是由最差的蚂蚁所产生的,它会使其他蚂蚁移动到难以接近目标点的位置上,或者会导致算法过早求解,为了获得良好的寻优性能,在每次迭代中,可使用以下更新规则增加最佳局部路径上的信息素浓度并降低最差局部路径上的信息素浓度。因此,对信息素更新规则公式改进为
(9)
(10)
(11)
其中STmax和STmin分别为ST的最大值和最小值,Loptimal和Lworst分别为最好和最差的局部路径长度。
改进算法按以上信息素更新规则方式进行路径搜索,能有效加快算法的收敛速度。
2.4 设置动态信息素挥发策略
在基本蚁群算法中,信息素挥发率ρ是(0,1)范围内的常数,直接影响着算法全局搜素能力和收敛速度,如果ρ太小,信息素挥发的较慢,会降低全局搜索能力,使算法陷入局部收敛。如果ρ过大,全局搜索能力会得到一定程度的提高,但收敛速度会降低。
为确保能在扩大搜索空间和加快收敛速度两者间取得良好的平衡,对信息素挥发率进行动态调整。其中,在算法开始时,将挥发率设置为较大的值,来改善全局搜索能力,然后挥发率将按如下公式进行改变
(12)
式中r和n分别为当前迭代次数和最大迭代次数;m为蚂蚁的数量,STk为蚂蚁k的ST;τmax和τmin分别为达到信息素量的最大值和最小值。
改进算法通过增加动态信息素挥发策略,能够扩大蚁群对室内空间的搜索范围,找寻到较优的路径,从而避免蚁群陷入局部最优。
3 算法改进与实现
3.1 改进蚁群算法的步骤
具体改进蚁群算法流程如图2所示。

图2 改进蚁群算法流程Fig.2 Improved ant colony algorithm flow chart
3.2 仿真实验环境构建与有效性分析
3.2.1 仿真实验环境的构建
为验证改进的蚁群算法在室内三维航迹规划的有效性,在三维栅格地图中对改进蚁群算法进行实验。实验仿真平台为MATLAB2018a,考虑到一架无人机和室内环境模型特点,且无人机可以向环境中任意方向运动飞行。该实验的规划空间分为10 m×10 m×10 m栅格,20 m×20 m×20 m栅格和30 m×20 m×15 m栅格,实验搭建的三维模型如图3所示,为更真实的接近室内场景,空间中随机设置障碍物。规定没有障碍物的空间栅格可以通过,有障碍物的空间栅格不可通过。
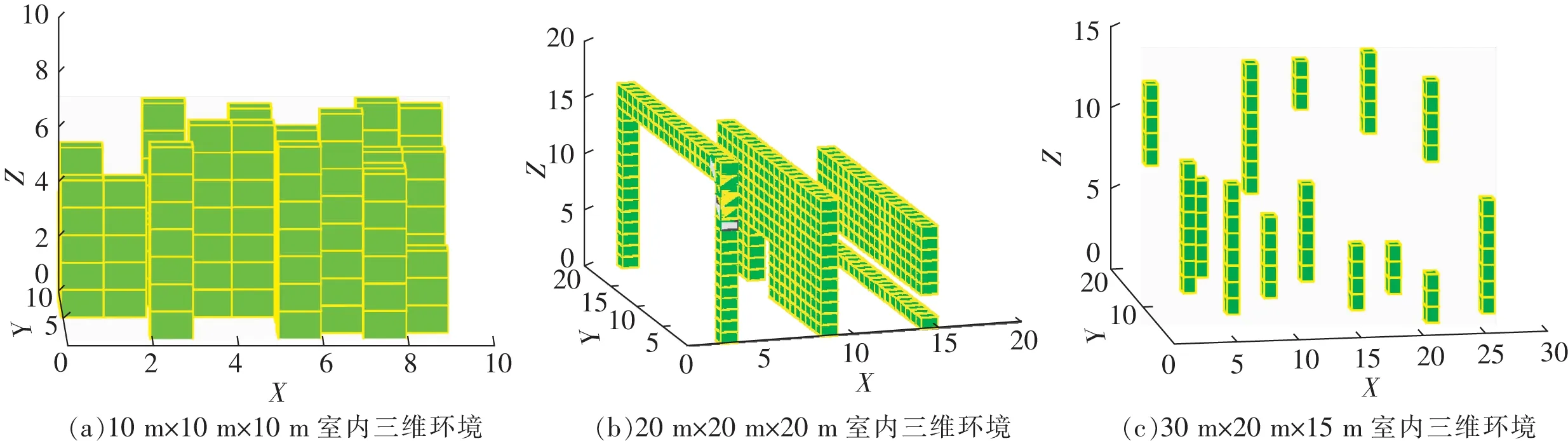
图3 不同尺度的室内三维环境模型Fig.3 Indoor three-dimensional environment models with different scales
在室内航迹规划中,算法参数设置如下:蚂蚁数量m=100,信息素浓度启发因子α=1,能见度启发因子β=2,挥发系数ρ=0.7,信息素强度Q=10,迭代次数n=50。
3.2.2 改进算法的实现及有效性验证
在不同空间规模的条件下,采用改进算法和基本算法在室内环境1(规模为10 m×10 m×10 m)、室内环境2(规模为20 m×20 m×20 m)和室内环境3(规模为20 m×30 m×15 m)中各进行20次重复航迹规划,然后从路径长度,收敛时间等角度来比较2种算法的实验效果,并对得到的结果进行对比和分析。为便于统计计算,对实验的相关结果保留至小数点后3位。3种室内空间规模中基本算法和改进算法所规划的路径以及最佳个体适应度变化情况分别如图4~图6所示。
图4~图6的实验结果表明,改进蚁群算法在3种不同的室内环境中经过计算迭代后,均能搜索到一条较优路径,并且搜索到的较优路径比基本蚁群算法的路径长度更短,如图4(b)、图5(b)、图6(b)中的蓝色路径相较于红色路径更短。这是因为在算法搜索初期,基本蚁群算法因缺乏初始信息素,对空间进行盲目搜索,使得所找寻到的路径较长。而改进算法对初始信息素调节因子进行改进,增强朝目标点方向的信息素浓度,避免算法出现盲目搜索的状况,从而找寻到一条较短路径,有效节约搜索时间。同时,在环境1中,障碍物的高度不一,分布也不均匀,改进算法所规划的路径选择离目标点距离近且周围障碍物少的路径通道,基本蚁群算法按传统的启发式规则随机选择可行通道,有时选择的可行通道节点离目标点较远。产生这2种结果的原因是改进算法中新设计的启发式概率有效扩展蚁群搜索视野并提高了蚁群可见性精度。
如图4(c)、图5(c)、图6(c)为3组实验的侧视图。图4(d)、图5(d)、图6(d)所反映的是最佳个体适应度值变化趋势,可以得出改进算法(蓝色曲线)比基本算法(红色曲线)的收敛迭代速度快,且当适应度值达到稳定后,改进算法所得到的适应度值比基本算法的小,并且改进算法的适应度值在算法前期搜索阶段,快速下降,出现这种结果是由于算法改进了信息素更新规则并采用信息素挥发率动态调整策略,从而加快算法的收敛速度,同时也扩大蚁群搜索范围,有效解决基本蚁群算法易陷入局部最优极值的问题。在环境1中,基本算法经过33次迭代后,其最佳个体的适应度值趋于稳定,且达到最优,而改进算法在迭代15次后,最佳个体的适应度值达到最优,如图4(d)所示。并且基本算法经过后续的多次迭代后,其最佳个体的适应度值仍高于改进算法相对应的值。从图5(d)可以看出,改进算法和基本算法分别经过19次、43次迭代后,适应度值达到最小。图6(d)中,改进算法和基本算法分别经过6次、8次迭代后,适应度值达到最小。
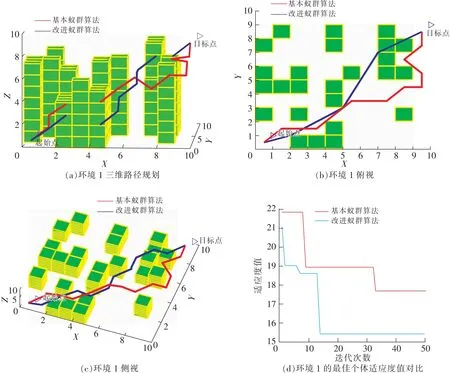
图4 室内环境1中2种算法仿真对比Fig.4 Simulation comparison of two algorithms in indoor environment Ⅰ

图5 室内环境2中2种算法仿真对比Fig.5 Simulation comparison of two algorithms in indoor environment II
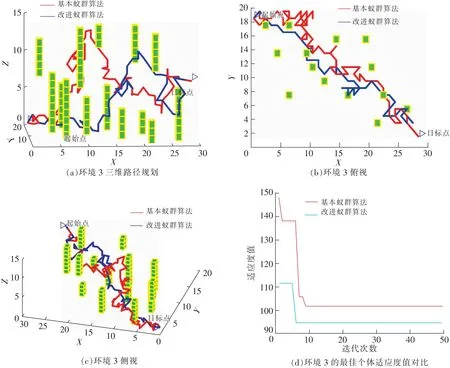
图6 室内环境3中2种算法仿真对比Fig.6 Simulation comparison of two algorithms in indoor environment Ⅲ
对2种蚁群算法在3种不同室内环境中重复实验得到的20条路径长度和算法所用时长进行统计比较,见表1。由表1可知,改进蚁群算法搜索的20条最优路径长度效率分别提高:11.8%,46.9%,57.2%,路径长度平均值效率分别提高17.7%,54.9%,62.7%。改进蚁群算法平均用时相较基本蚁群算法而言,提升较小。具体来说,在室内空间规模较小的环境1中,2种算法都能较快搜索到最优解,搜索到的路径长度平均值和算法用时两方面的效率百分比相差不大。

表1 3种室内环境中的2种算法性能比较Table 1 Performance comparison of two algorithms in three indoor environments
伴随着室内空间范围扩大,改进算法的各项性能逐渐显现,同时路径长度效率提升趋势与算法用时效率提升趋势呈一升一降2种相反的变化结果。分析可知,这是由于改进算法在寻找较优路径时,随着空间范围的增大,相应地空间搜索计算量也增大,从而导致所用时间增大,算法用时的提升效率也随之降低。
3.2.3 算法适应性验证
为验证所提出的改进算法在不同场景下的适应性,在不同障碍物和目标位置点中分别进行3组实验,每次实验运行多次并使结果保留至小数点后3位。图7~图9显示3组实验的路径规划图。其中图7(b)在图7(a)基础上改变目标点位置,图8(b)与图8(a)为相同起始点和目标点条件下的室内不同障碍物环境,图9(a)和图9(b)为完全不同的室内环境和目标点。

图7 不同目标点的三维规划Fig.7 Three-dimensional planning diagram of different target points
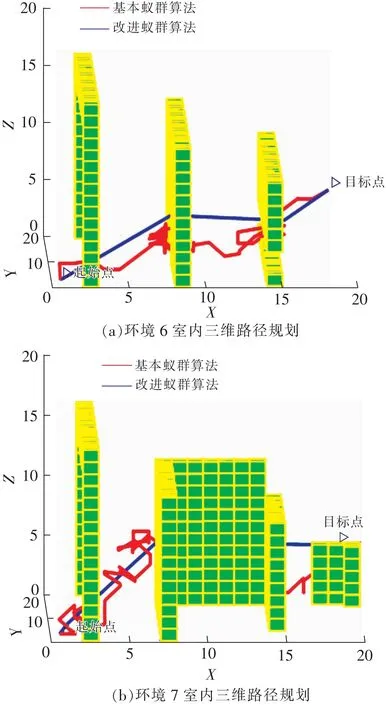
图8 室内空间障碍物位置不同Fig.8 Different indoor spatial obstacle positions
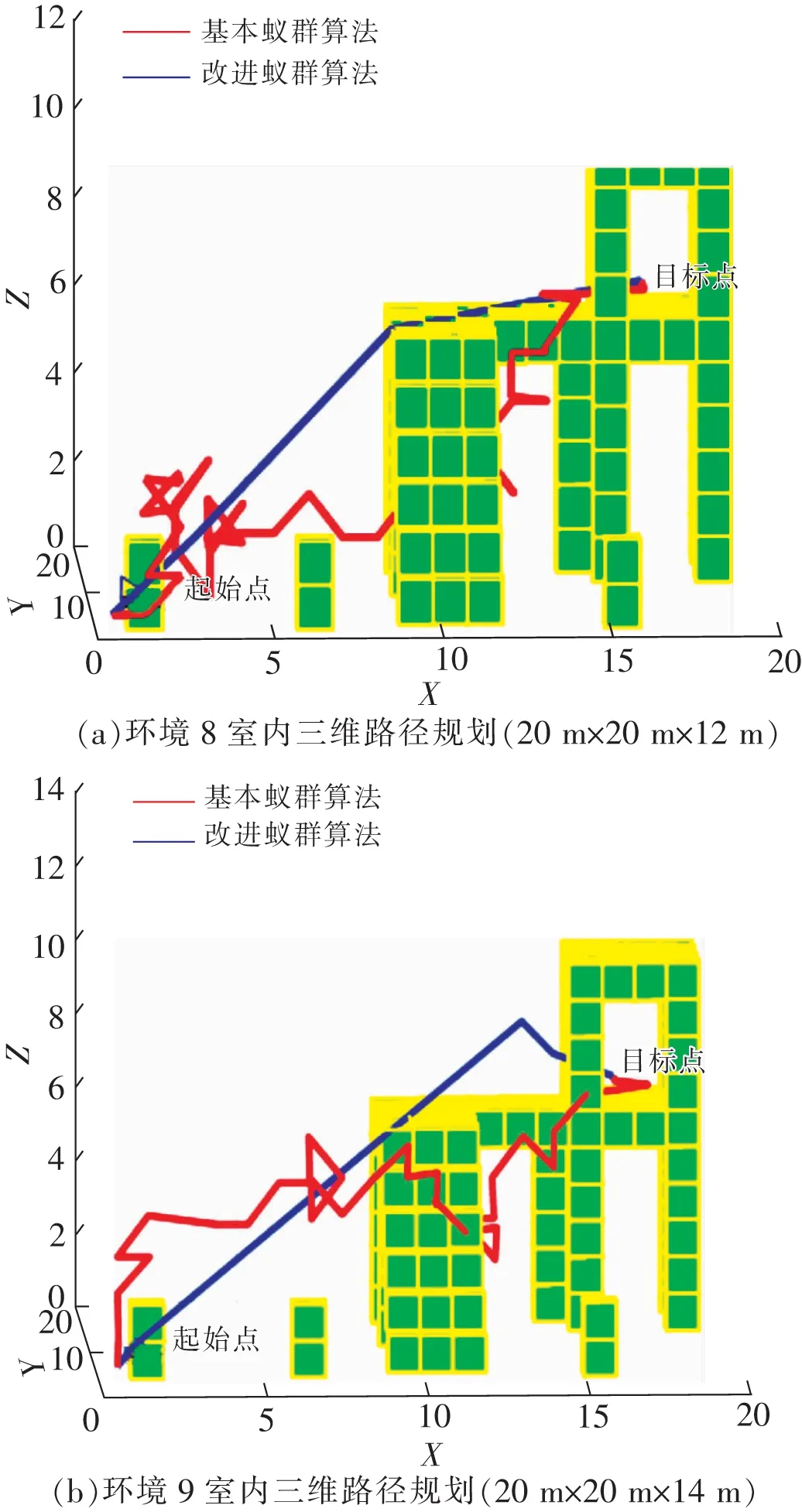
图9 空间范围不同Fig.9 Different spatial scopes
从图7可以看出,实验更改无人机所要到达的目标位置,规划的路径仍能够安全避开障碍物并准确到达目标点,由于图7(a)和图7(b)起始点坐标都为(1,1,1),图7(a)目标点坐标是(9,10,7),图7(b)目标点坐标是(10,9,8),所以图7(b)实验得到的路径规划长度、算法计算用时、迭代次数都大于图7(a)的值。图8(a)与图8(b)因障碍物差异较大,且图8(a)中的无人机直接通过第2、第3个障碍物下方的通道到达目标点,但在图8(b)中,由于第2个障碍物是一个类似U型的障碍物,则无人机需要先不断沿y轴方向搜索,再转向x轴方向搜索到达目标点,最终导致改进算法搜索到的最优路径长度、算法用时、收敛迭代次数不同。在第3组实验中,由于室内空间范围由图9(a)的20 m×20 m×12 m扩展为图9(b)的20 m×20 m×14 m,使得图9(b)中采用改进算法所规划的路径长度比图9(a)的路径长度更长。表2为图7~图9这3组实验得到的数据结果。
表2结果说明,改变不同的条件,所提出的改进算法在不同的场景下有着很好的适应性,同时通过实验验证改进算法的路径规划性能指标与无人机起始点和目标点的距离大小、空间复杂度大小、空间范围大小这3种因素有关。
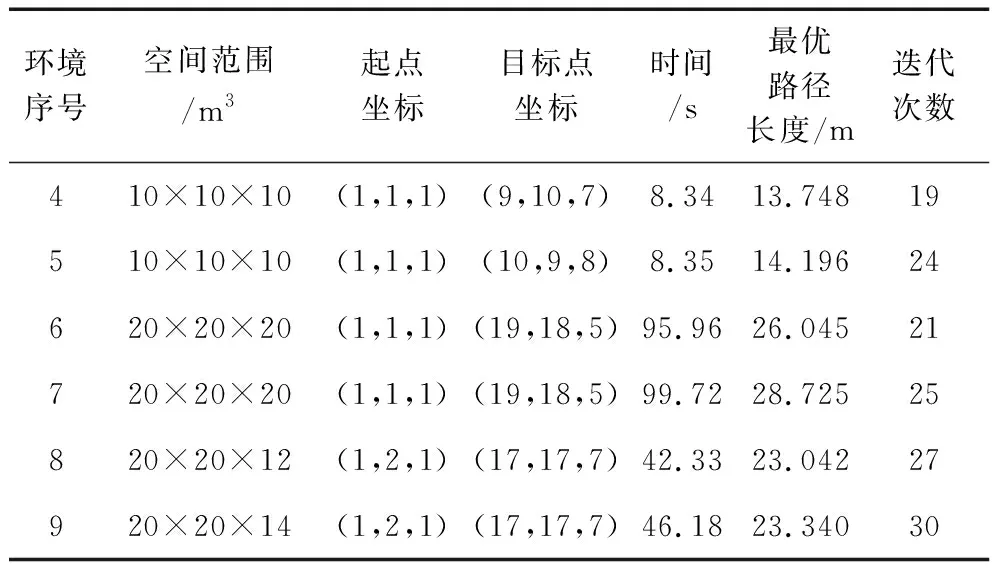
表2 不同环境中改进蚁群算法的性能比较Table 2 Performance comparison of improved ant colony algorithm in different environments
4 结 论
1)针对传统蚁群算法存在初期盲目搜索、易陷入局部最优、收敛速度慢等问题,提出一种优化蚁群算法,通过改进初始信息素调节因子,进而增强蚁群搜索的方向性。
2)设计一种启发概率函数,扩展蚁群搜索视野并提高可见性,使得最优路径长度比基本蚁群算法缩短38.6%,平均用时减少3.8%。
3)对信息素更新规则进行改进,增添信息素挥发动态调整策略,从而加快算法收敛迭代速度,有效验证改进算法在复杂环境中的良好适应性。
