基于稳健估计局部多项式插值定权模型分析
2022-04-28刘亚静李胜男王诚聪
刘亚静,李胜男,王诚聪
(1.华北理工大学 矿业工程学院,河北 唐山 063210;2.中国科学院 东北地理与农业生态研究所,吉林 长春 130000)
0 引 言
局部多项式插值法是一种局部加权最小二乘拟合,根据有限个已知采样点数据,采用多个多项式来进行曲面的拟合[1],每一个插值点的预测值都对应一个多项式,利用局部多项式插值法得到的曲面,能够较好地描述短程变异[2]。在测量过程中,由于受到诸多因素的影响,会使测量数据中含有粗差,使得观测值将不服从正态分布,若直接使用这些数据进行曲面插值,其结果很难与真实情况相吻合[3]。抗差估计解决了这一问题,即使用等价权函数来代替一般权函数,对含粗差的数据进行降权处理,则可以有效提高模型的抗差能力。
在现有研究中,吴富梅等利用水准网数据,对选权迭代法的几种权函数在不同显著性水平下的抗差性进行了比较,认为当数据不稳定时,IGGⅢ和丹麦法的抗差效果略优于其他权函数[4]。徐波、杨勇喜等通过坐标参数转换实例对选权迭代法进行分析,发现通过IGG函数进行定权可有效降低含粗差观测值的权值,在进行三维坐标转换时能获取更高精度的转换参数[5-6]。孙同贺等将具有稳健初值的选权迭代法融入到DEM粗差探测中,证实稳健初值的选权迭代法具有很强的稳健性和粗差探测能力,可以实现对粗差的探测和剔除[7]。HOLLAND等提出选权迭代法,可通过反复迭代,逐步减小粗差观测值的权重,从而进行粗差定位和剔除[8]。稳健估计选权迭代法具有很好的抗差能力[9],但其相关研究大多是针对水准网测量和坐标转换方面的研究,对于多项式插值采样点的定权鲜有阐述。
一般认为DEM误差来源于源数据的采样误差和DEM插值过程中的插值误差[10]。在进行多项式插值时,常用的采样点定权函数包括反距离加权法和局部距离比法,但对于含粗差的观测数据,这2种传统的方法会将粗差当作一般数据处理,导致在构建曲面模型时粗差引入,使得曲面发生歪曲[11-14]。因此文中将稳健估计选权迭代法与局部多项式插值进行结合,分别采用传统的反距离加权法和稳健估计选权迭代法中的Huber权函数法、Andrews权函数法、IGG方案对局部多项式插值的采样点进行定权,通过均方根误差(root mean squared error,RMSE)对各方法的拟合精度进行比较分析,并且对比分析采用不同定权方法得到的插值曲面和预测高程相似度,探讨所引进的3种定权方法中,在数据含有粗差时采用不同定权方法降低含粗差观测值的权[15-17],对于含粗差数据插值拟合效果最优的方法,以提高其插值精度,对局部多项式插值的定权模型改进,为局部多项式插值曲面的建立提供保证。
1 局部插值理论模型与精度评定
1.1 动态球半径选点法
动态球半径选点法是以内插点为球心,R为半径,选取各内插点周围可用来计算的采样点[18-19](图1)。半径R可通过构造函数来确定
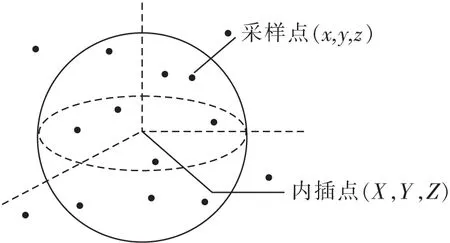
图1 动态球半径选点法原理示意Fig.1 Schematic diagram of dynamic sphere radius point selection method

(1)
式中N为采样点总数,个;A为研究区域面积,m2;n为规定界限球内的采样点数,个。
1.2 二次曲面模型
高精度曲面的绘制必须保证每一个数据点在权值其有效范围内平滑过渡[11],采用二阶可导的二次曲面来建立局部曲面模型,其二次曲面模型表达式如下
z=f(x,y)+ε
(2)
f(x,y)=a0+a1x+a2y+a3xy+a4x2+a5y2
(3)
式中z为插值点高程值,m;ε为拟合残差;f(x,y)为二次曲面点的内插值,m,ai(i=0,1,2,…,5)为多项式系数;x和y分别为平面采样点的横纵坐标。
通过最小二乘原理,求解多项式系数,矩阵表达形式如下
Z=B×A+ε
(4)
A=(BTPB)-1(BTPε)
(5)
矩阵表示为
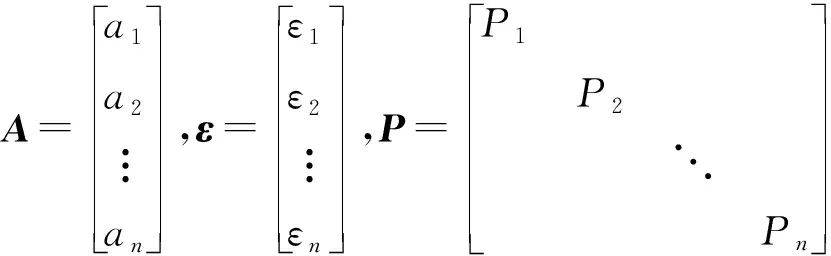
1.3 精度评定
选用均方根误差(RMSE)进行拟合优度的评价,当预测值与真实值相同RMSE=0,误差越大,该值越大。均方根误差计算公式为
(6)

2 采样点权函数
采样点权函数可以用来反映采样点与内插点的相关程度。对区域内的采样点赋权,权重(Pi)的确定与该点到内插点的距离(di)有关,距离越小,该点对内插点的影响就越大,权重也越大。可采用反距离加权法、Huber权函数、Andrews权函数和IGG方案4种方法确定采样点的权重。
多具有不规则状晶形,与石英、云母等脉石矿物关系密切,少部分与黄铁矿连体,白钨矿中含钨约为60.81%,粒度主要为中细粒,占75.14%,部分为微细粒,占12.02%,少量为粗粒,约占12.82%。矿石中的白钨矿解离度较好,-0.074 mm含量占65%的磨矿细度下,92.73%的白钨矿已单体解离,6.49%的白钨矿与脉石矿物共生。因此,白钨矿主要分为两类,一类多数为单体解离,但粒度大小差别较大。另一类粒度较细,与脉石矿物与石英、长石等脉石矿物共生或呈港湾状接触,或包裹于脉石矿物颗粒中。
2.1 反距离加权法
反距离加权法是常用的采样点定权法。该方法依据相近相似的原理[20],采样点权重的大小会随着其与插值点之间距离的增大而减小,距离插值点越近,采样点的权重就越大[14]。
(7)
(8)
式中di为内插点到采样点的距离,m;X,Y,Z分别为内插点的坐标;xi,yi,zi分别为采样点的坐标。
2.2 稳健估计权函数
采用稳健估计权函数进行采样点的定权,是以内插点与采样点之间的距离为自变量,内插点的值为因变量[18],通过采样点权函数计算其权重。权函数分别选用Huber权函数、Andrews权函数和IGG方案,其中Huber函数包含正常域和可疑域,只对可疑域内的观测值进行降权处理,不能将有害信息剔除掉;Andrews函数包含可疑域和淘汰域,将所有的观测值都进行降权处理;而IGG方案同时拥有正常域、可疑域和淘汰域,充分利用所有观测数据[4]。
2.2.1 Huber权函数
Huber权函数确定的权因子为
(9)
式中ω为采样点权因子;u为采样点残差。
2.2.2 Andrews权函数
(10)
式中ω为采样点权因子;u为采样点残差。
2.2.3 IGG方案
IGG方案是由周文江教授最初提出的[21],该方案将数据划分为正常、可用和有害数据,同时,将权分区为保权区、降权区及淘汰区,充分考虑测量数据的实际情况,很好地将不同权重函数和容差标准用于不同的测量数据。由IGG方案确定的权因子[16]为
(11)
式中vi为第i个测量的残差;σ0为标准偏差;k,r为阈值的调制因子,其中k=1.0~1.5,r=2.5~3.0,该方案k=1.5,r=3.0。
由式(11)可知,IGG方案将权重确定分为3部分,采用不间断抗差标准[22]:当残差不大于kσ0时,采用最小二乘法,其权重仍为1;当残差介于kσ0与rσ0时,则采用残差反比例减少法,降低对其权重,以减弱对参数识别的影响;当残差大于rσ0时,其权重为0,即淘汰此测量数据,充分体现IGG方案的抗差能力。
3 案例分析
3.1 数据来源
实验采用《ArcGIS地理信息系统空间分析实验教程》中的实验数据。该组数据共有170个采样点,分布均匀,属性字段分别是横坐标x,纵坐标y,以及高程z。部分采样点数据见表1。
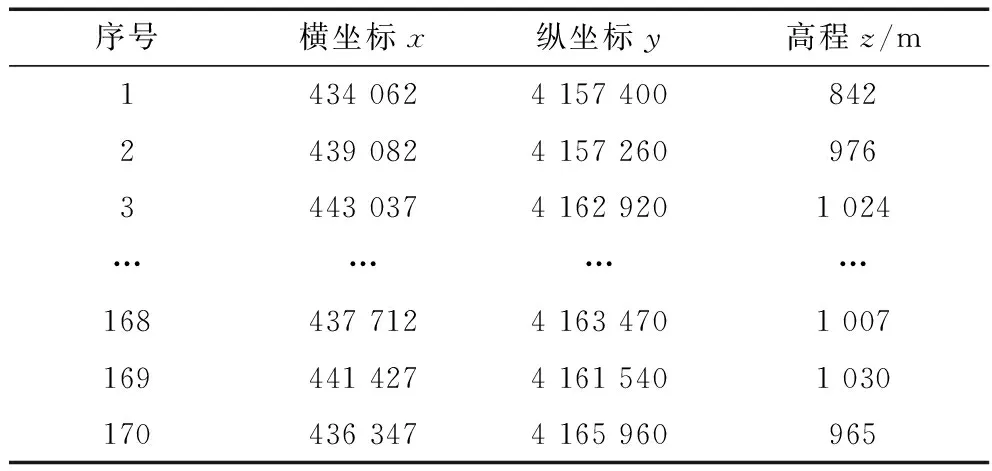
表1 部分采样点数据Table 1 Partial sampling points data
为验证Huber函数法、Andrews函数法及IGG方案对含有粗差数据的抗差性强度区别,在实验数据中随机加入3组粗差。运用MATLAB软件进行曲面插值和拟合,并在三维空间中显示出来(图2),同时将稳健估计采样点定权3种方法预测得到的高程数据进行对比分析,通过散点图表示(图3)。
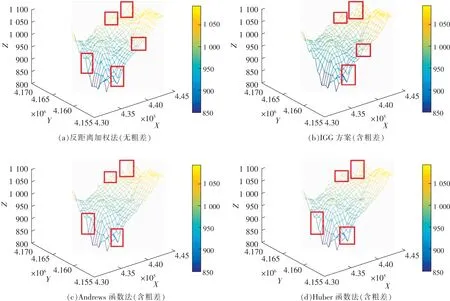
图2 曲面拟合结果对比Fig.2 Comparison of curved surface fitting results
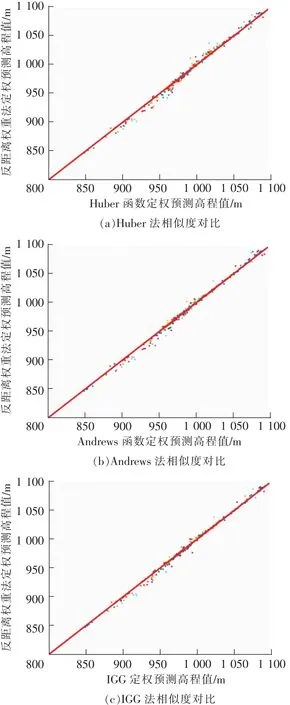
图3 插值结果相似度对比Fig.3 Similarity comparison of interpolation results
3.2 插值曲面对比分析
对比分析图2中的拟合曲面效果,可以看出选权迭代法对含有粗差的数据进行定权的插值结果与无粗差数据时结果很接近,效果较好,图中标注的部分为插值曲面中差异较明显的区域。
3.3 预测高程相似度对比分析
将采用反距离加权法对无粗差数据计算出的高程,与采用稳健估计权函数对于含粗差数据计算出的高程,通过散点图(图3)来反应其结果的相似程度。纵轴代表数据无粗差时采用反距离权重法定权得到的高程值,横轴表示采用选权迭代法计算出的高程值。
图3中3幅图像数据点的分布均呈现出y=x的趋势,但由IGG方案定权后进行插值拟合的效果更好,说明当数据存在粗差时,3种选权迭代法中,采用IGG方案对采样点进行定权预测的内插点高程值,与数据无粗差时常用的反距离权重法进行定权计算得到的高程结果最为接近。
3.4 拟合优度对比
当测量数据含有粗差时,通过对比4种采样点定权方法得到的均方根误差(RMSE)评价其曲面拟合优度(见表2),RMSE越大,则说明预测值与真实值的误差越大[23-26],即抗差性越弱。由表2可知,当高程数据含有粗差,采用传统的反距离加权法进行插值时,RMSE值为1.433 3,相比之下,Huber函数法和Andrews函数法插值得到的拟合优度更高,分别是0.742 8和0.683 2,表明稳健估计选权迭代法具有一定的抗差能力。当采用IGG方案对采样点进行定权时,RMSE最小为0.531 8,可以看出该方法的抗差能力最强,因此可以推断当观测数据存在误差时,所用的3种方法中,IGG方案对采样点定权所得到的高程值与真实值最为接近,拟合度最高,插值效果最好。

表2 含粗差时拟合优度对比Table 2 Analysis of goodness of fit with gross error
4 结 论
1)在局部多项式插值中,当数据存在粗差时,利用传统的反距离权重法定权会将粗差当作一般数据进行处理,因此在构建曲面模型时会因粗差的存在而使曲面发生扭曲,与真实情况下的插值结果差别较大。运用选权迭代法将稳健估计思想运用到空间确定性插值中,在一定程度上能使插值结果不受粗差的影响。
2)通过实例得出,在对含粗差数据进行多项式插值时,采用稳健估计选权迭代中的IGG方案对采样点定权,经过多次迭代,可使含有粗差的观测值权降为零或接近零,减弱粗差对插值结果的影响,且IGG方案对采样点定权的方法优于传统的反距离权重法与选权迭代的Huber函数法和Andrews函数法。
3)将抗差估计的思想融入到局部多项式插值模型中,设计出对粗差具有抵抗能力的插值模型,对于提高局部多项式插值的准确性具有很强的现实意义,但由于IGG方案中k,r的2个阈值调制因子取值的不同,会导致插值结果有所不同,因此对该方案插值模型中的参数取值仍需进行优化。
