改进贝叶斯判别法的矿井水源识别模型
2022-04-28秋兴国黄润青
秋兴国,刘 杰,李 娜,黄润青
(西安科技大学 计算机科学与技术学院,陕西 西安 710054)
0 引 言
中国是世界主要产煤国之一,也是受煤矿水害最严重的国家之一[1],在煤矿井下发生的水害水灾是矿井安全工作中的关注重点[2],矿井水害一旦发生将会造成极为严重的人员伤亡及财产损失,所以只要及时准确地识别矿井水源就可以采取有效的防治措施。因此,在水害防治工作中,对于矿井水源识别工作是重中之重。目前,水源识别方法包括地下水化学特征分析法、多元统计方法(判别分析法和聚类分析方法)和非线性分析方法(模糊数学法、神经网络法和可拓识别法等)[3-4]。陈俊环等利用水质类型的差异,对矿井水源进行判别,并说明水化学分析法存在一定的局限性[5];袁文华等将水温水位判别法应用于煤矿水源的判别,建立地温方程计算含水层水温,与实际监测点水温进行比较来判别矿井水源[6];孙福勋等利用Fisher判别理论,结合质心距评判法对矿区水样进行了分析判断[7];代革联等在煤矿中引用模糊聚类判别法,分析了水质类型相似时水源判别不准确的问题[8];徐星等利用神经网络仿真结果误差小的特点将其应用于矿井突水水源判别领域[9];张瑞钢等利用可拓识别方法判别矿井突水水源,还有一些未确知数学方法等[10]。而上述方法各有适用性,如有的模型复杂、判别过程繁琐、确定离子权重时主观性较强、对误判损失有失考量[11],在准确率方面也需要提高等,因此矿井水源识别的算法研究还需进一步深入。
贝叶斯判别法具有判别模型简单、求解速度较快和判别质量高的特点[12],在贝叶斯判别法的基础上,结合主成分分析方法,并引入变异系数来进行评估计算过程中水质离子的权重,以消除水源判别过程中离子指标间存在信息叠加以及评价过程中主观因素过重带来的影响[13],提高水源判别的准确率,从而减少实际应用中矿井水源类别的误判。
1 理论与算法
1.1 主成分分析法
主成分分析法(principal component analysis,PCA)是一种降维的统计方法,将可能互相关联的多个元素进行数据压缩,重新组合成一组新的相互无关的元素,达到以尽可能少的数据来表示大部分信息的目的[14]。
由于在数据处理过程中难免会遇到高维数据组,由于数据维数较高变量较大,这些变量之间往往会存在一些相关性,因此这些数据样本很难反映总体的主要特征[15]。主成分分析将可能具有相关性的高维变量经过线性变换合成线性无关的低维向量,用来提取较少个数的重要变量。在矿井水源识别工作中,经过主成分分析可以在保留主要信息的基础上降低向判别模型输入的维数,减小输入信息量,达到以少量的水质离子就可以代表某类水源的目的,若主成分选取有误差,在实际的水源识别工作中则会类别模糊不清或对最终的判别结果产生影响。利用Statistical Product and Service Solution(SPSS 24)对原始数据进行主成分分析处理。
假设对某一事物的研究涉及N个样本,每个样本有n个变量,分别用X1,X2,…,Xp表示,对随机变量进行线性变换形成新的综合变量Y[16],即
(1)
式中ci1+ci2+…+cin=1;Yi与Yj(i≠j;i,j=1,2,…,n)互相无关;Yi为(Y1,Y2,…,Yn)的线性组合中方差最大者;Y2为与Y1不相关的(X1,X2,…,Xn)所有线性组合中方差最大者;Yn为与(Y1,Y2,…,Yn-1)都不相关的(X1,X2,…,Xn)的所有线性组合中的方差最大者[17]。基于以上原则确定的综合变量(Y1,Y2,…,Yn)分别称为样本的第1,第2,…、第n个主成分[18]。主成分分析法的主要过程如下。
1)对原始数据进行标准化处理,排除数量级和量纲对结果造成的影响。
2)计算各标量之间的协方差矩阵及相应特征向量与特征值。
3)计算第k个主成分的方差贡献率(k=1,2,…,n)。
4)按照累积方差贡献率>80%或特征值大于1的原则选取主成分[19]。
1.2 贝叶斯判别法
贝叶斯(Bayes)是先通过已给定的训练集,以特征词之间的独立作为前提假设,学习从输入到输出的联合概率分布,再基于已学习的模型,输入X输出拥有最大后验概率的Y,其中X=(x1,x2,…,xn)为判别指标;n为判别指标的维数;Y为类别[20]。
1.2.1 贝叶斯模型
贝叶斯计算公式为
(2)
式中Bi为水源类别;A为水样;P(Bi)为先验概率,即未经计算仅通过经验和直觉来判断该水样属于某种水源的概率;P(A|Bi)为条件概率,即当水样属于不同水源时出现某种水质离子的概率;P(Bi|A)为后验概率,即当获得水质离子测量值的条件下该水样属于某种水源的概率。
针对矿井水源水质离子的特点,将贝叶斯模型细化,并对贝叶斯模型中的参数做进一步调整:i为水样中的水质离子指标;j为某种水源;(i=1,2,3,…,n)(j=1,2,3,…,m)。因此,原贝叶斯公式修改为
(3)
式中xi为水样中第i个水质离子的监测值;yij为当水源种类为j时水质离子i的标准值。
1.2.2 贝叶斯模型计算步骤
1)计算P(yij),即未经计算水质离子就判断该水样属于哪种水源,此时水样属于每种水源的概率值相同。
(4)
2)计算P(xi|yij),此处采用距离方法[21],即取水质离子的监测值与标准值间距离绝对值的倒数进行计算[22],即
(5)
式中Lij=|xi-yij|,(i=1,2,3,…,n)。
3)计算,P(yij|xi)按照式(3)计算。
4)求多种水质离子综合时水样属于水源的概率,其中ωi为水质离子i的权重。
(6)
5)以最大概率确定水样归属
(7)
1.3 变异系数法
变异系数法(coefficient of variation method)是利用各项指标所含信息来计算指标的权重,是一种客观赋权方法。这种方法的基本做法是:在评价体系中取值越大的指标,越能反映该项指标的重要程度。变异系数越大说明该离子的重要程度越大,该水质离子在水样中起的作用就越大,越能代表该水样,故可用变异系数确定的变异性权重来确定水质离子的重要程度。通过变异系数法来计算权重,避免了主观赋权方法中专家的偏好对结果的影响[23-24]。数据处理步骤如下。
1)数据标准化
将第i个指标的实际数值记为Xi,该组数据的最大值记为Xmax,最小值记为Xmin,数据标准化之后的值记为Zi,通过公式计算[25]。
(8)

(9)
3)计算各指标赋权重
(10)
1.4 改进贝叶斯判别的矿井水源判别模型
在对主成分分析、变异性权重和贝叶斯判别模型相结合后,构成了改进贝叶斯判别模型。并在此基础上建立起改进贝叶斯矿井水源识别模型(图1)。

图1 改进贝叶斯判别的矿井水源识别模型Fig.1 Mine water source identification model of improved Bayesian discrimination
矿井水源识别模型的实验步骤(图2)为:①整理水源数据,进行数据标准化,计算协方差矩阵、特征向量、特征值,写出主成分并根据主成分贡献率来选取在水源中起主要作用的水质离子;②根据总水源种类计算水样的先验概率;③计算变异系数,在多指标综合计算概率时代替原公式中的权重w(数据标准化、计算标准差和变异系数);④推求多指标综合下的后验概率;⑤以最大概率归属原则确定该水样归属。
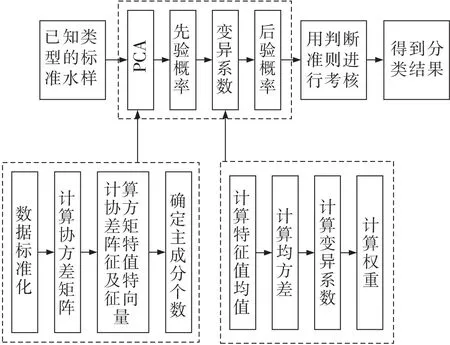
图2 改进贝叶斯判别模型结构Fig.2 Model structure of improved Bayesian discrimination
2 矿井水源判别模型建立
2.1 数据准备

2.2 主成分分析法
在相关系数矩阵中,若相关性小于0.3,说明离子间存在弱相关;若相关性在0.3与0.6间,说明离子直接存在中等强度关系;若相关性大于0.6,则离子间存在强相关关系(表2)。说明各水质离子间存在相关关系和重叠信息,例如Ca2+和Mg2+关联度达到了92.9%。若直接使用冗余重叠信息进行判断,有可能会对判别结果产生影响,所以要进行降维来减少参与判别模型的水质离子数量。
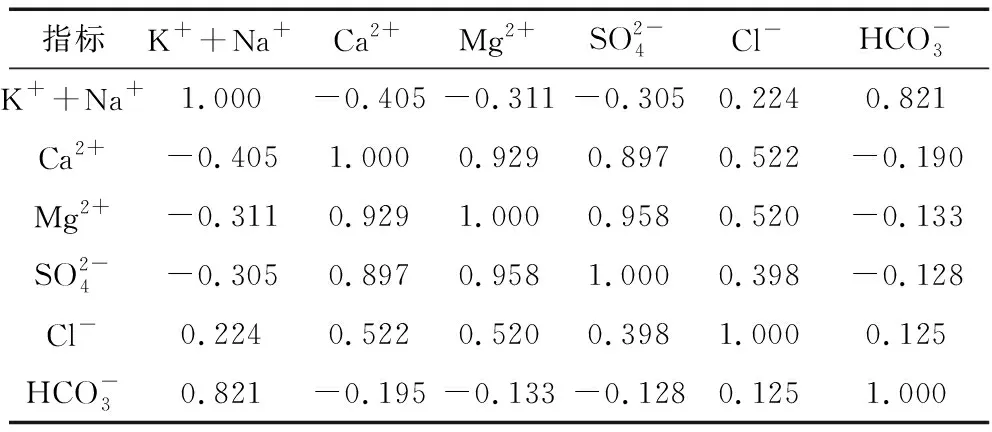
表2 水化学指标相关系数Table 2 Correlation coefficients of hydrochemical index
通过对各主成分进行方差贡献率(表3)分析,可以根据需要来选取需要的主成分。前5个水质离子的累积方差贡献率达到了99.55%,说明这5个水质离子几乎完全可以代表水样中所有离子的特征。

表3 成分方差贡献率Table 3 Contribution rate of component variance
2.3 权重确立
根据2.2确定的2.1表1中(1-26号)主要水质离子,以及1.3对于变异系数法的论述,通过MATLAB软件实现各主要水质离子的权重的计算(表4)。

表4 变异性权重
2.4 贝叶斯模型及判别结果
根据1.2中贝叶斯方法的原理及步骤,对表1中作为数据标准的数据(1~26号)进行回代检验以及对表1中待检测样本数据(27~40号)进行判别并与直接贝叶斯判别进行对比。

表1 屯兰矿水化学特征Table 1 Hydrochemical characteristics of Tunlan mine
在14个矿井水源数据待判样本中,改进的贝叶斯模型判别正确个数为 11个,原始贝叶斯模型判别正确10个。基础贝叶斯判别误判个数为5个,总体正确率为64.29%,而改进的判别模型误判个数为2个,总体正确率为85.71%(表5)。

表5 预测结果对比Table 5 Comparison of prediction results
从表6可以看出,在26个回代数据中,改进的贝叶斯模型判别正确个数为25个,原始贝叶斯模型判别正确 24个;贝叶斯判别正确率为92.31%,改进的贝叶斯方法正确率为96.15%。结果表明,改进后的方法更加准确,判别准确率更高。
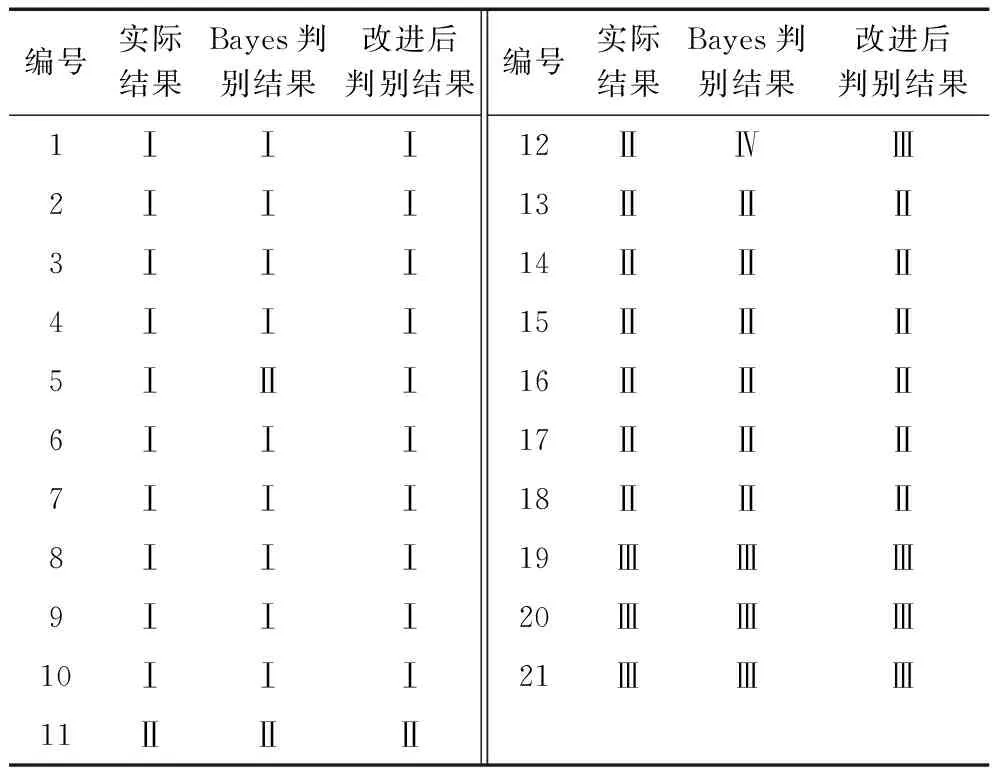
表6 样本回代结果Table 6 Sample back-substitution results
根据基础贝叶斯判别模型和改进贝叶斯判别模型,对待测样本进行水源类型的归属判别。从结果(图3)中可以看出第5,第6,第9,第11,第13个水源数据类别判别有误,而改进后的贝叶斯判别法后只在第6,第9个水源类型判别有误。

图3 预测结果对比Fig.3 Comparison of prediction results
图4表示对样本数据回代进行水源类别的归属判别,在实验中基础贝叶斯判别在第5,第12个水源数据类别判别有误,而改进后的贝叶斯判别法仅在第12个水源数据判误。

图4 样本回代结果Fig.4 Sample back-substitution results
在待测样本数据类型判别中改进的贝叶斯模型较基础贝叶斯模型的准确率从64.29%提升到85.71%,提升了21.42%,而回代样本从92.3%提升到96.15%,提升了3.85%,说明改进后的算法准确率有显著的提升(表7)。

表7 模型预测结果比较Table 7 Comparison of model prediction results
3 结 论
1)经主成分分析后的水质离子维数降低,降维后的数据能够很好地保留原数据的基本信息,提取出起主要作用的水质离子,避免因信息叠加和人为选取水质主成分的主观性;通过变异系数来客观赋予权值可去量纲化及消除人为赋予权值的影响,并且较为客观地反映水质离子在样本中的重要程度,能够识别指标数据的变化信息。
2)样本回代组和样本测试组的判别准确率较传统贝叶斯模型有明显提高,判别结果可信度高,为水源判别提供了一种新的识别思路,可为矿山防治水提供依据。
