基于BP-QR模型的负荷区间预测

陈轩伟

基于BP-QR模型的负荷区间预测

陈轩伟

（厦门大学嘉庚学院，福建 漳州 363105）

为了减少负荷预测中电网运行不确定因素产生的误差，本文结合BP神经网络与分位数回归（QR）算法，提出基于BP-QR模型的负荷区间预测方法，以气象因素与前一日用电负荷值作输入，实现当日负荷区间预测。实验结果表明，该模型能准确反映用电负荷的波动趋势，可实现任意置信水平下的区间预测，为电力调度提供参考信息。

负荷预测；区间预测；分位数回归；神经网络

0 引言

国家电网有限公司于2019年提出了“三型两网”的战略目标[1]，旨在充分应用传感测量、人工智能等现代先进技术，实现电力系统各环节的信息互联与智能分析。有效的电力负荷预测可以辅助电力调度部门经济准确地制定生产计划和运行方式，是“三型两网”建设中实现电网发电侧与需求侧有效贯通的重要桥梁之一。

目前，负荷预测主要有灰色关联分析[2]、时序分析法[3]、神经网络[4-5]、支持向量机[6-7]等几类方法。随着深度学习的提出，深度神经网络[8-10]算法逐渐成为负荷预测研究中的代表。深度神经网络具有特征自学习能力，在学习数据充分的情况下可用于拟合复杂非线性系统，但其训练速度慢，参数多样性也增加了网络训练的难度。

上述方法多用于对负荷确定点的预测，即预测模型输出为确定值。然而电网发电侧与需求侧存在众多不确定因素，点预测方法对负荷预测的不确定性描述有限，使电力生产决策面临一定风险。相比于点预测，区间预测方法扩大了预测模型的输出范围，减少了不确定因素对预测精度的影响，能够让电网决策人员了解未来负荷的波动情况，具有重要的工程意义。

分位数回归（quantile regression, QR）模型可计算不同分位点结果，从而获得给定置信区间下的预测量变化区间[11]。文献[12]结合改进后的BP神经网络和分位数回归实现不同天气下光伏出力的区间预测。文献[13]基于极限学习机和分位数回归预测光伏出力区间，结果表明该模型训练时间短且精度高。上述研究将机器学习算法与分位数回归结合，实现光伏出力的区间预测。文献[14]利用卷积神经网络提取负荷数据特征，结合长短期记忆神经网络与分位数回归实现日前负荷区间预测，该方法具有较好的区间预测性能，但其算法复杂，训练耗时长。

本文引入分位数回归对简单BP神经网络模型进行误差分析，以气象因素及前一日用电负荷值为输入特征，搭建BP-QR区间预测模型，实现不同置信水平下的用电负荷区间预测。通过算例分析表明，该模型简单有效，且具有较好的置信水平适应性。

1 分位数回归原理

分位数回归由Koenker与Bassett提出[15]，给定权重值，通过线性回归求解最小误差，实现分位数回归，其数学描述如下。

令随机变量的分布函数为

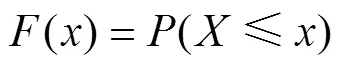
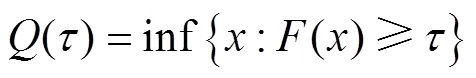
假定样本序列{(x,y),(=1,…,)}满足分位数回归模型，其方程为

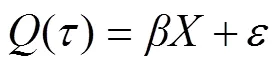
式中：为参数；为随机变量。

令误差绝对值之和最小，采用改进单纯形法计算回归方程中参数的估计值为

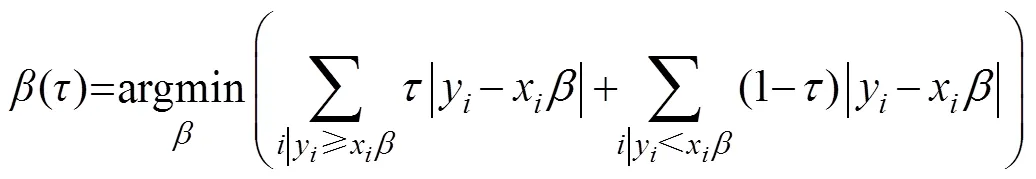
2 BP-QR区间预测模型

分位数回归是一种线性回归算法，一般结合其他预测模型实现区间预测。BP神经网络是经典机器学习算法之一，能够拟合非线性数据，具有应用简单、泛化能力强等优点。本文结合两种算法，提出BP-QR区间预测模型结构框图，如图1所示。

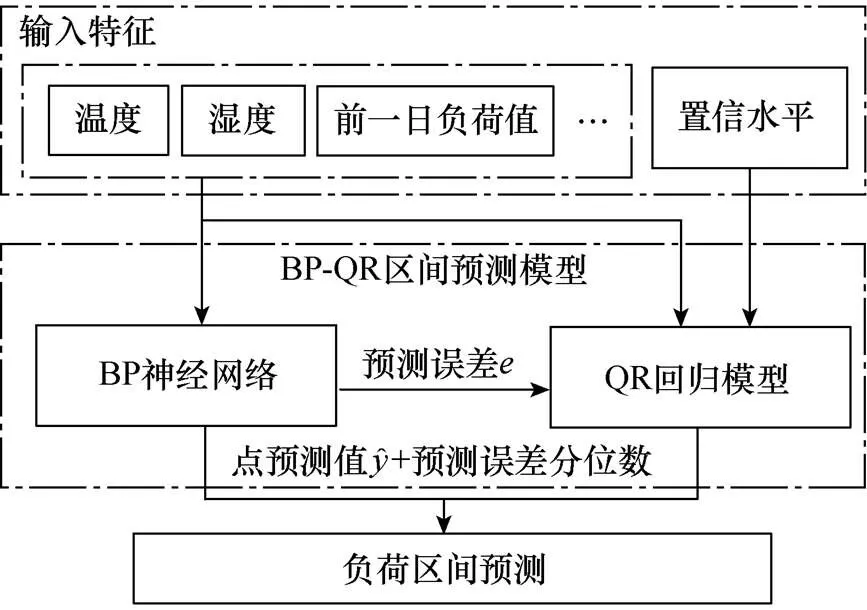
图1 BP-QR区间预测模型结构框图

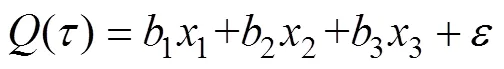
式中：123为参数；123为输入特征，本文中输入特征为预测时刻对应的温度、降雨量及上一时刻的实际用电量；为随机误差。采用单纯形法计算累计误差最小时不同分位数下的参数，建立误差分位数回归模型。最后，将BP神经网络中的点预测结果和QR回归模型计算的误差分位数相加，实现负荷区间预测。

2.1 数据预处理

输入数据量纲的不同将导致数值大的变量对模型的影响大，而数值小的变量影响小，因此在模型训练前，有必要对数据进行归一化处理，使输入数据映射为0～1之间的数，消除量纲不同对模型的 影响。

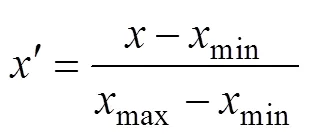
式中，max和min分别为变量的最大值和最小值。

2.2 BP神经网络点预测模型

BP神经网络由输入层、隐藏层及输出层组成，各层中包含若干神经元，神经元由线性求和运算和激活函数组成。线性求和是指将输入神经元的数据线性叠加，激活函数将线性叠加的结果非线性化。单个神经元的表达式为

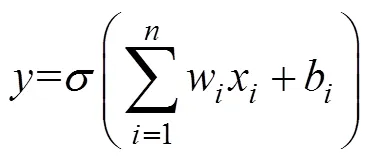
式中：为神经元的输出；为权重值；为偏置值；为激活函数，常见的激活函数有relu、sigmoid、tanh等。

以评价指标作为BP神经网络的损失函数，通过梯度下降法训练网络，经过迭代找到最优解，其计算公式为

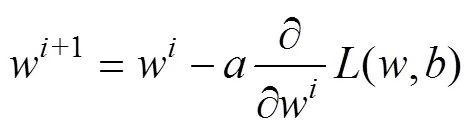
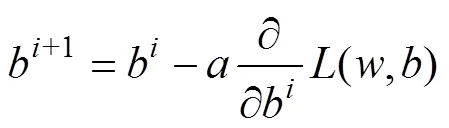
式中：为学习率；()为损失函数；、含义同上。根据负荷数据，基于梯度下降法不断迭代更新参数，实现神经网络对输入输出间非线性关系的最优拟合，进而实现负荷预测。

2.3 评价指标

本文采用平均绝对百分比误差（mean absolute percentage error, MAPE）作为负荷点预测的评价指标，采用区间覆盖率和平均宽度作为负荷区间预测的评价指标，平均绝对百分比误差计算公式为

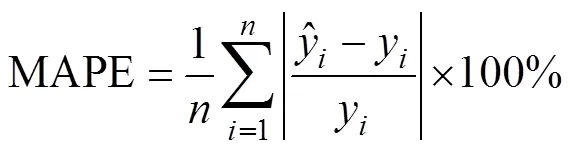
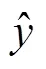
用相对平均宽度描述区间预测结果的波动范围大小，其计算公式为

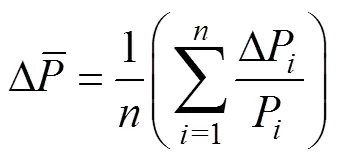
预测区间覆盖率指实际负荷值落在预测区间内的概率，描述区间预测的准确性，其计算公式为

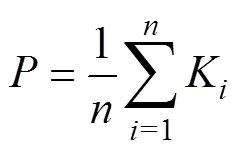
式中：为样本个数；为布尔量，当实际负荷值落在预测区间内时，为1，否则为0。

3 算例分析

为了验证BP-QR模型的预测效果，本文以某地区2012年01月～2015年01月的电力负荷数据建立预测模型，该数据来源于全国大学生电工数学建模竞赛，数据包含每日电力负荷值、气象因素（日最高气温、日最低气温、日平均气温、日相对湿度及日降雨量），实验算法均基于Python 3.7仿真实现。

3.1 基于BP神经网络的点预测模型

本文选用数据集中的当日气象因素及前一日电力总负荷值为模型输入，以当日用电总负荷为输出，每组数据时间间隔一天，取70%数据作为训练集，30%作为测试集进行模型训练。BP神经网络选用计算简单的激活函数relu实现网络的非线性化，并针对隐藏层神经元数量与学习率两个参数进行调参，以MAPE值作为评价指标，训练结果见表1。根据训练结果，选择学习率为0.01，隐藏层为两层，第一层50个、第二层10个神经元的BP神经网络为电力负荷点预测模型。

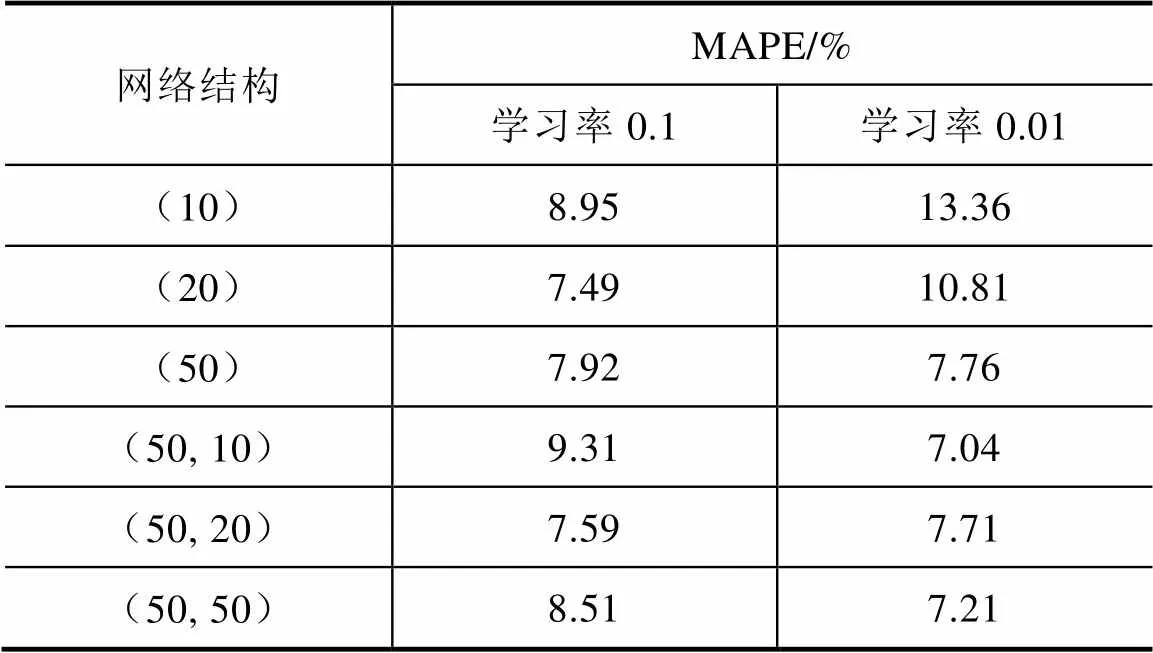
表1 训练结果

3.2 BP-QR模型适用性分析

基于BP点预测模型的预测误差搭建分位数回归（QR）模型，根据气象因素和前一日负荷值计算出分位数回归参数，结合点预测结果实现区间预测。计算90%、80%和70%置信水平下区间预测的相对平均宽度及测试集数据预测覆盖率，BP-QR预测模型区间预测结果见表2。

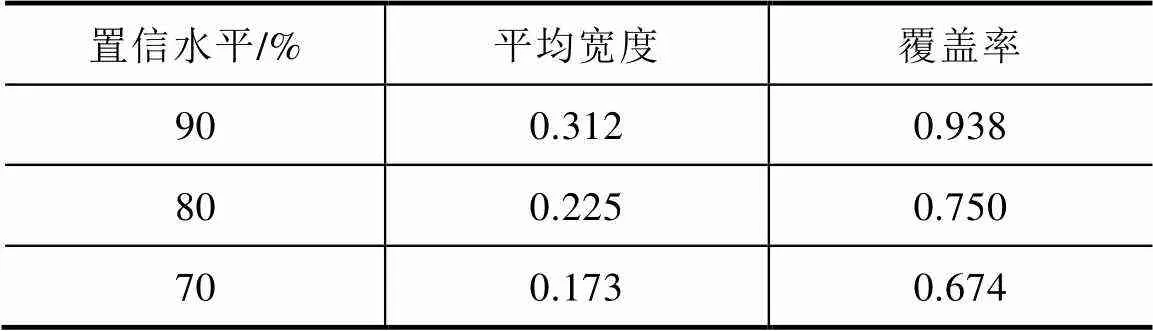
表2 BP-QR预测模型区间预测结果

从表2可以看出，区间平均宽度随着置信水平的降低而减小；覆盖率随平均宽度减小而减低。区间覆盖率与置信水平基本一致，算例结果验证了本文提出的BP-QR模型的有效性。

为了进一步说明区间预测效果，本文分别在70%、80%及90%置信水平下，截取测试集中2014年03月28日～2014年06月15日共计80天数据样本的预测结果，分别如图2～图4所示。

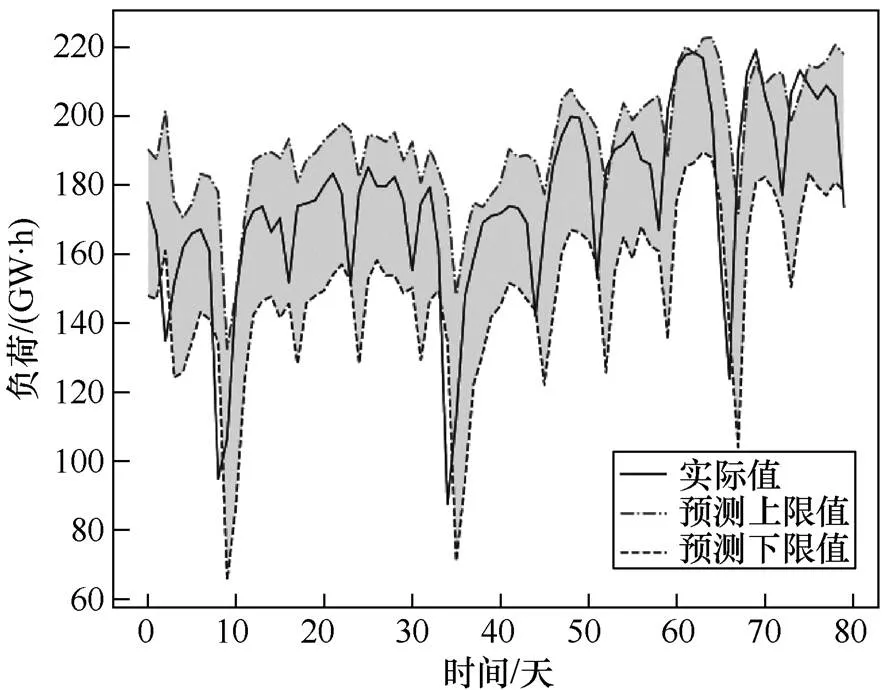
图2 90%置信水平下的预测结果

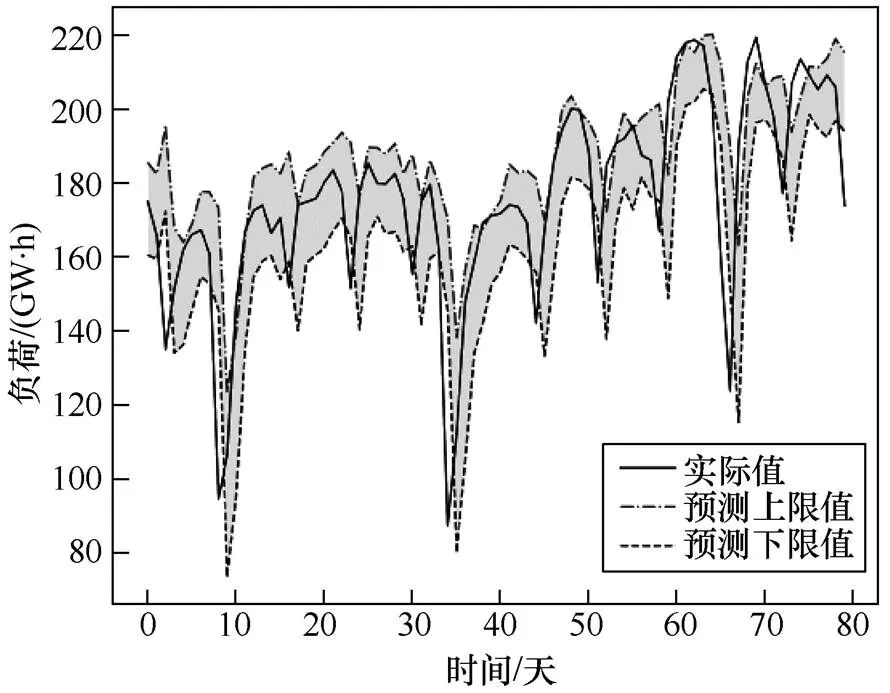
图3 80%置信水平下的预测结果

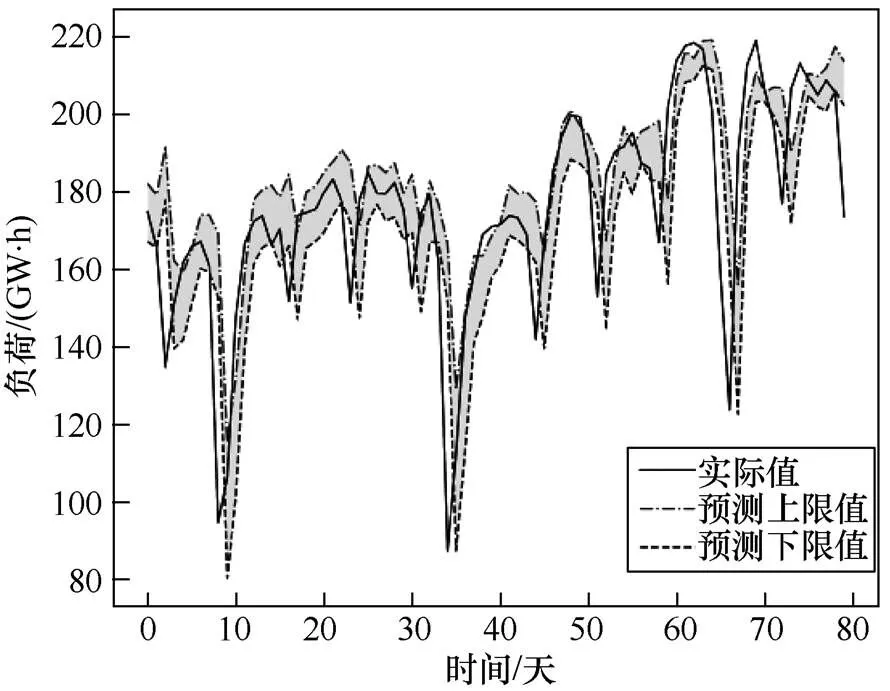
图4 70%置信水平下的预测结果

由图2～图4可知，BP-QR区间预测模型总体上能反映出负荷波动趋势，随置信水平的减小，区间宽度减小，使预测误差增加。此外，可以看出预测误差主要来源于负荷快速变动及峰谷期间。

为了更好地验证BP-QR模型预测效果，将BP-QR模型与QR模型、正态分布模型进行对比：QR模型基于同样的输入特征，但不引入BP神经网络，仅通过分位数回归预测区间上下限；正态分布模型基于BP神经网络误差，通过标准正态分布表计算误差分位点记为区间上下限。给定置信水平90%和80%，不同模型区间预测结果见表3。

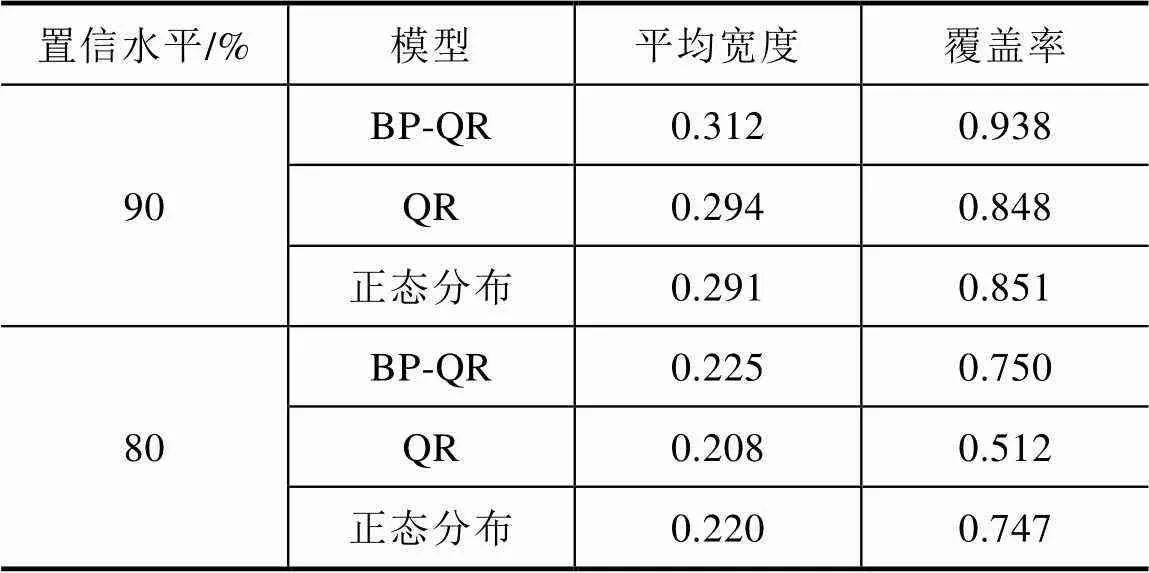
表3 不同模型区间预测结果

从表3可以看出，在置信水平90%时，本文提出的BP-QR区间预测模型能更准确地覆盖实际负荷值；在80%置信水平下，BP-QR模型与正态分布模型覆盖率相当。综上可知，在不同置信水平下，BP-QR模型都具有较高的准确性。

4 结论

针对负荷点预测方法中电网运行不确定因素带来的局限性，本文基于BP神经网络与分位数回归算法，提出了BP-QR负荷区间预测模型，模型输入为气象因素与前一日用电负荷值，输出为当日用电负荷区间。算例结果表明，该模型准确反映了用电负荷的波动趋势，相比于QR模型和正态分布模型，具有更高的预测精度，可用于短期负荷预测，为电力调度提供参考。

此外，算例误差主要集中在波动较大的区间中，这类波动由于节假日等特殊情况产生，因此在未来研究中，可引入其他输入特征进一步提高预测精度。

[1] 寇伟. 如何建设“三型两网”[J]. 中国电力企业管理, 2019(10): 20-21.

[2] 林天祥, 张宁, 胡军. 基于优化权重的卡尔曼滤波与无偏灰色组合模型的短期负荷预测[J]. 电气技术, 2017, 18(9): 19-23.

[3] 张帅, 杨晶显, 刘继春, 等. 基于多尺度时序建模与估计的电力负荷数据恢复[J]. 电工技术学报, 2020, 35(13): 2736-2746.

[4] FENG Yu, XU Xianfeng, MENG Yun. Short-term load forecasting with tensor partial least squares-neural network[J]. Energies, 2019, 12(6): 990.

[5] 徐扬, 张紫涛. 基于遗传模拟退火算法改进BP神经网络的中长期电力负荷预测[J]. 电气技术, 2021, 22(9): 70-76.

[6] 唐承娥, 韦军. 改进的支持向量回归机在电力负荷预测中的应用[J]. 计算机科学, 2020, 47(增刊1): 58-65.

[7] ZHANG Xiaobo, WANG Jianzhou, ZHANG Kequan. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm[J]. Electric Power Systems Research, 2017, 146: 270-285.

[8] 李玉志, 刘晓亮, 邢方方, 等. 基于Bi-LSTM和特征关联性分析的日尖峰负荷预测[J]. 电网技术, 2021, 45(7): 2719-2730.

[9] MOON J, JUNG S, REW J, et al. Combination of short-term load forecasting models based on a stacking ensemble approach[J]. Energy and Buildings, 2020, 216: 109921.

[10] 林珊, 王红, 齐林海, 等. 基于条件生成对抗网络的短期负荷预测[J]. 电力系统自动化, 2021, 45(11): 52-60.

[11] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201- 1217.

[12] 贾德香, 吕干云, 林芬, 等. 基于SAPSO-BP和分位数回归的光伏功率区间预测[J]. 电力系统保护与控制, 2021, 49(10): 20-26.

[13] WAN Can, LIN Jin, SONG Yonghua, et al. Pro- babilistic forecasting of photovoltaic generation: an efficient statistical approach[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2471-2472.

[14] 唐戈, 余一平, 秦川, 等. 基于CNN-LSTM分位数回归的母线负荷日前区间预测[J]. 电力工程技术, 2021, 40(4): 123-129.

[15] 陈建宝, 丁军军. 分位数回归技术综述[J]. 统计与信息论坛, 2008, 23(3): 89-96.

Load interval forecasting based on BP-QR model

CHEN Xuanwei

(Xiamen University Tan Kah Kee College, Zhangzhou, Fujian 363105)

This paper combines BP neural network and quantile regression (QR) algorithm to propose a load interval forecasting method to reduce the errors caused by the uncertain factors of power grid operation. The load interval forecasting is realized by the meteorological factors and the previous day’s load value. The experimental results show that the model can show the fluctuation trend of electricity load accurately, and provide forecasting intervals under any confidence level.

load forecasting; interval forecasting; quantile regression; neural network

厦门大学嘉庚学院校级孵化项目（YM2020L04）

2021-10-08

2021-11-05

陈轩伟（1994—），男，福建宁德人，硕士，助教，主要从事智能微电网方面的研究工作。