柴油机单个主轴承变形协调特性评价方法及影响规律研究

赵鑫，苏铁熊，刘晓勇，任日娜

(1.中北大学机电工程学院，山西 太原 030051；2.中北大学能源动力工程学院，山西 太原 030051；3.中北大学机械工程学院，山西 太原 030051)

在我国碳达峰和节能减排的发展背景下，高功率密度是新时期动力发展的必然趋势。相比于传统柴油机，高功率密度柴油机具有高紧凑性、高燃烧压力及高转速等特点。曲轴轴承系统是内燃机最主要的结构单元之一，由于功率密度提升导致主轴承所受工作载荷大幅增加，主轴承失圆变形增加，进而引发变形失效，这对整机可靠性产生了不可忽略的影响。

为保证柴油机主轴承的工作可靠性，研究人员针对主轴承变形开展了大量的研究。董玉光和曹晓辉等模拟了螺栓预紧工况下精镗主轴承孔时的整机应力状态，重点考察主轴承孔的同轴度、圆柱度和圆跳动。王磊和廖日东等基于对失圆度、偏心度等指标的计算，对安装状态下主轴承孔及主轴瓦的变形进行了综合评价与分析。当前，主轴承变形的研究主要聚焦于描述单个主轴承横截面变形特性的失圆度，描述多个主轴承整体变形的同轴度、圆柱度和圆跳动等，而罕有针对主轴承及其配合副(曲轴)之间变形协调特性评价方法及影响规律的研究。吴斌辉分析了主轴承在多工况下的刚度情况，提出了单个主轴承变形、多个主轴承整体变形及单个主轴承变形协调特性的评价方法，但文献中主轴承变形协调特性评价指标的计算过程相对复杂，且该计算方法对主轴瓦、曲轴有限元模型的网格划分均有一定要求。综上，针对主轴承变形协调特性的评价指标进行更加深入的研究具有重要意义。

本研究提出以主轴瓦最大径向变形量作为单个主轴承变形协调特性的评价指标，深入探讨主轴瓦最大径向变形量的数值计算方法，并对其进行试验验证。基于设计参数对主轴瓦最大径向变形量的灵敏度分析，揭示典型设计参数对主轴承变形协调特性的影响规律及影响机制。

1 模型的建立

1.1 有限元模型的建立与边界条件的确定

以某高功率密度柴油机为研究对象，建立主轴承组合结构的单隔板有限元模型，其中包括机体、主轴承盖、主轴瓦、曲轴及连接螺栓(见图1)。

图1 主轴承组合结构有限元模型

位移边界条件：对主轴承组合结构单隔板模型的两侧对称面施加对称位移约束；机体、主轴承盖、主轴瓦及曲轴之间的接触均采用“面对面”接触方式；机体与主轴承盖侧壁采用间隙装配；主轴瓦与主轴承孔采用过盈装配。

力边界条件：在静力学分析中，主轴承组合结构只承受三方面载荷，分别为螺栓紧固载荷、主轴瓦过盈载荷及来自曲轴的主轴承载荷；预紧工况下，主轴承组合结构受螺栓紧固载荷和主轴瓦过盈载荷，且主轴承孔在螺栓紧固后进行了镗孔工艺；主轴承载荷工况下，主轴承组合结构在预紧工况的基础上还承受主轴承载荷。

根据本研究中机型的实际工况，确定单根竖拉螺栓预紧力为200 kN，单根横拉螺栓预紧力为98 kN，主轴瓦的初始装配过盈量为0.16 mm，机体与主轴承盖侧壁的初始装配间隙为0.1 mm。以该柴油机一个工作循环内较为恶劣的主轴承载荷作为计算加载值，该力在竖直方向上的分量为-78 365 N，水平方向上的分量为-195 769 N。

1.2 网格无关性验证

为了兼顾有限元仿真分析的计算效率与计算准确性，规划了5种不同尺寸的网格划分方案(见表1)。选取主轴承载荷工况下4个主轴瓦轴向截面的失圆度作为考察指标，截面1至截面4的坐标分别为-20 mm，-10 mm，10 mm，20 mm。

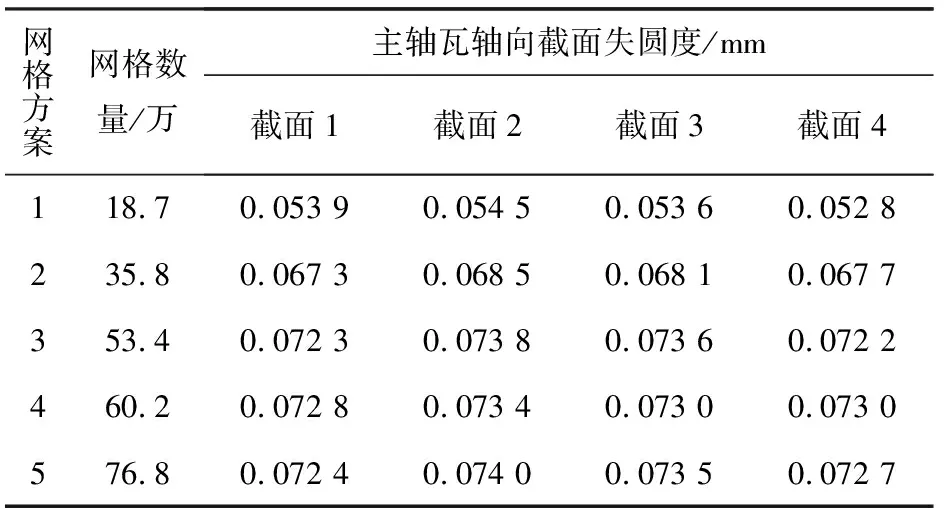
表1 网格无关性验证方案及结果

分析表中数据可以发现，方案1与方案2相比于其他方案各轴向截面的失圆度误差较大。对于方案3至方案5，其各截面失圆度的误差很小，能够控制在5%以内，故可以认为网格划分方案3至方案5达到了网格无关性的要求。综合考虑模型的计算效率和计算精度后，选择方案3对主轴承组合结构有限元模型进行网格划分。

2 主轴承变形协调特性评价方法

本研究拟采用主轴瓦最大径向变形量作为主轴承变形协调特性的评价指标。由于主轴承组合结构的静力学分析中模型加载的主轴承载荷恒定，可忽略曲轴轴颈径向变形对主轴承变形协调特性的影响。根据主轴瓦与曲轴的装配方式与加载方式分析，主轴承载荷主要分布在主轴瓦的径向，故忽略主轴瓦轴向的变形。

2.1 主轴瓦最大径向变形量的定义

主轴瓦最大径向变形量定义：主轴瓦变形后其直径方向上最大“压扁”变形量。主轴瓦变形前后某轴向截面轮廓线如图2所示。图2中，虚线表示曲轴的轮廓线。设曲轴轴颈的直径为，主轴瓦变形前的直径为。节点和节点受载后发生变形分别移动到和，二者在直径方向上的变形量分别为和，则节点和节点在直径方向上“压扁”的变形量为与之和，即Δ=+。若主轴瓦在其直径方向上有对节点发生变形，则其变形量分别为Δ，Δ，Δ，…Δ。

则主轴瓦最大径向变形量可表示为

max_Δ=max(Δ，Δ，Δ，…Δ) 。

(1)

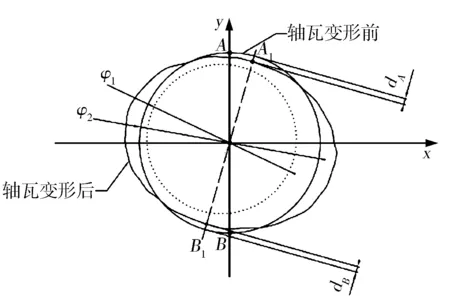
图2 主轴瓦径向变形量示意

2.2 主轴瓦最大径向变形量的计算方法

根据主轴瓦最大径向变形量的定义，制订如图3所示的主轴瓦最大径向变形量的计算流程。

2.2.1 主轴瓦变形后节点坐标的获取

本研究采用Abaqus软件进行有限元分析。对模型进行网格划分时应尽量保证上下主轴瓦网格规模相同。在后处理程序中建立两个×2的矩阵，提取上下轴瓦的节点坐标分别赋值到两矩阵中。

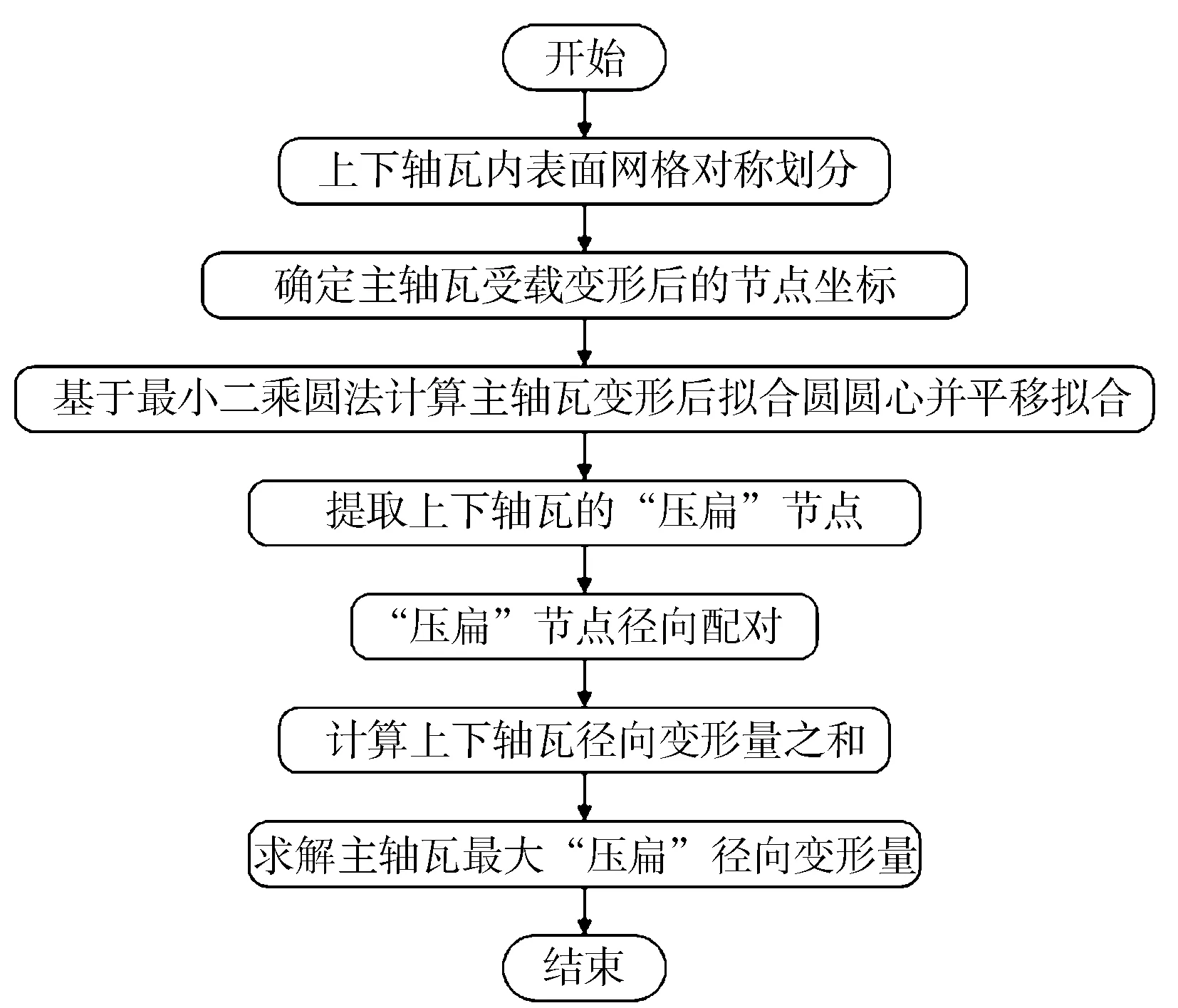
图3 主轴瓦最大径向变形量计算方法

2.2.2 主轴瓦变形后拟合圆圆心坐标计算

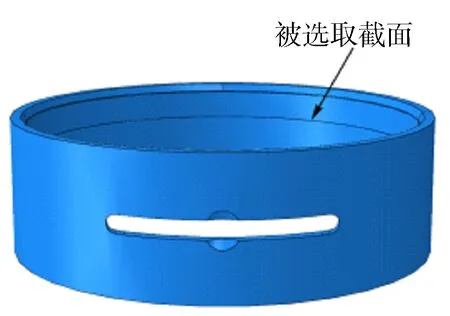
图4 被选取轴向截面示意

任取主轴瓦轴向上的某一截面(如图4所示)。设主轴瓦被选取的轴向截面的坐标为=，其内表面有个节点落在该轴向截面上，则变形后的坐标为(,)，=1,2,3,…。基于最小二乘圆法对主轴瓦变形后拟合圆圆心坐标进行求解。

根据圆的曲线方程

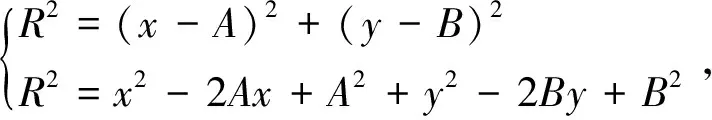
(2)

令

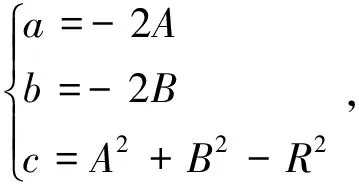
(3)

可以得到圆曲线方程的另一个形式：

++++=0。

(4)

求参数,,即可求得主轴瓦变形后轮廓线的拟合圆圆心坐标(,)及半径。主轴瓦变形后节点到圆心的距离满足

=(-)+(-)。

(5)

变形后节点(,)到拟合圆边缘的距离的平方与半径平方的差可表示为

=-=(-)+(-)-=
++++。

(6)

令(,,)为的平方和：

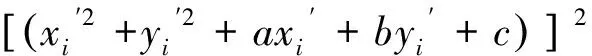
(7)

依据最小二乘法原理，求参数,,使(,,)的值最小。将(,,)对,,求偏导，求解所有极值点，其中函数值最小的极值点即为(,,)的最小值。

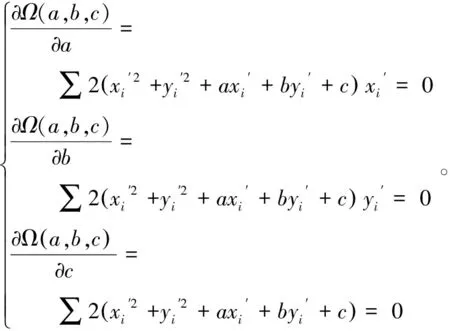
(8)

令

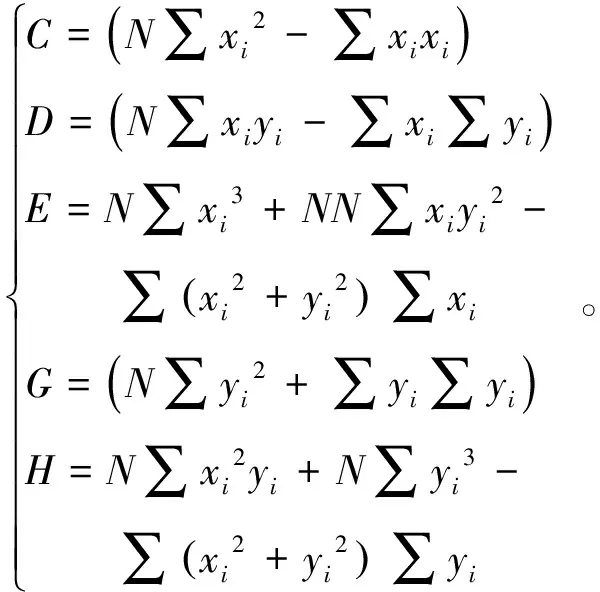
采用消去法对式(8)进行求解，解得

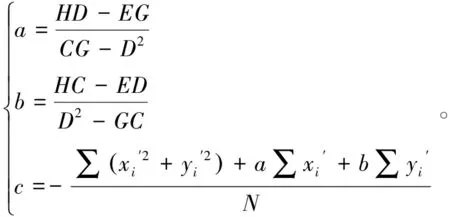
(9)

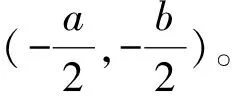
为了便于计算，设主轴瓦变形前的圆心位于原点。将主轴瓦变形后的拟合圆整体平移，使其与主轴瓦变形前的圆心重合，以消除刚体位移对主轴瓦径向变形量的影响，经过平移的节点坐标可表示为

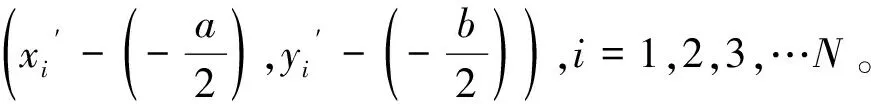
2.2.3 主轴瓦变形后“压扁”节点的选取

根据主轴瓦变形特征分析可知，主轴瓦变形后与曲轴在方向上不可能发生运动干涉，二者的运动干涉只可能发生在变形后的“压扁”节点之间(如图5所示)。设节点为“压扁”节点，其受载后变形至节点，此时有<。故可总结得出“压扁”节点的特征为：轴瓦变形后节点到原点的距离小于变形前该节点到原点的距离。

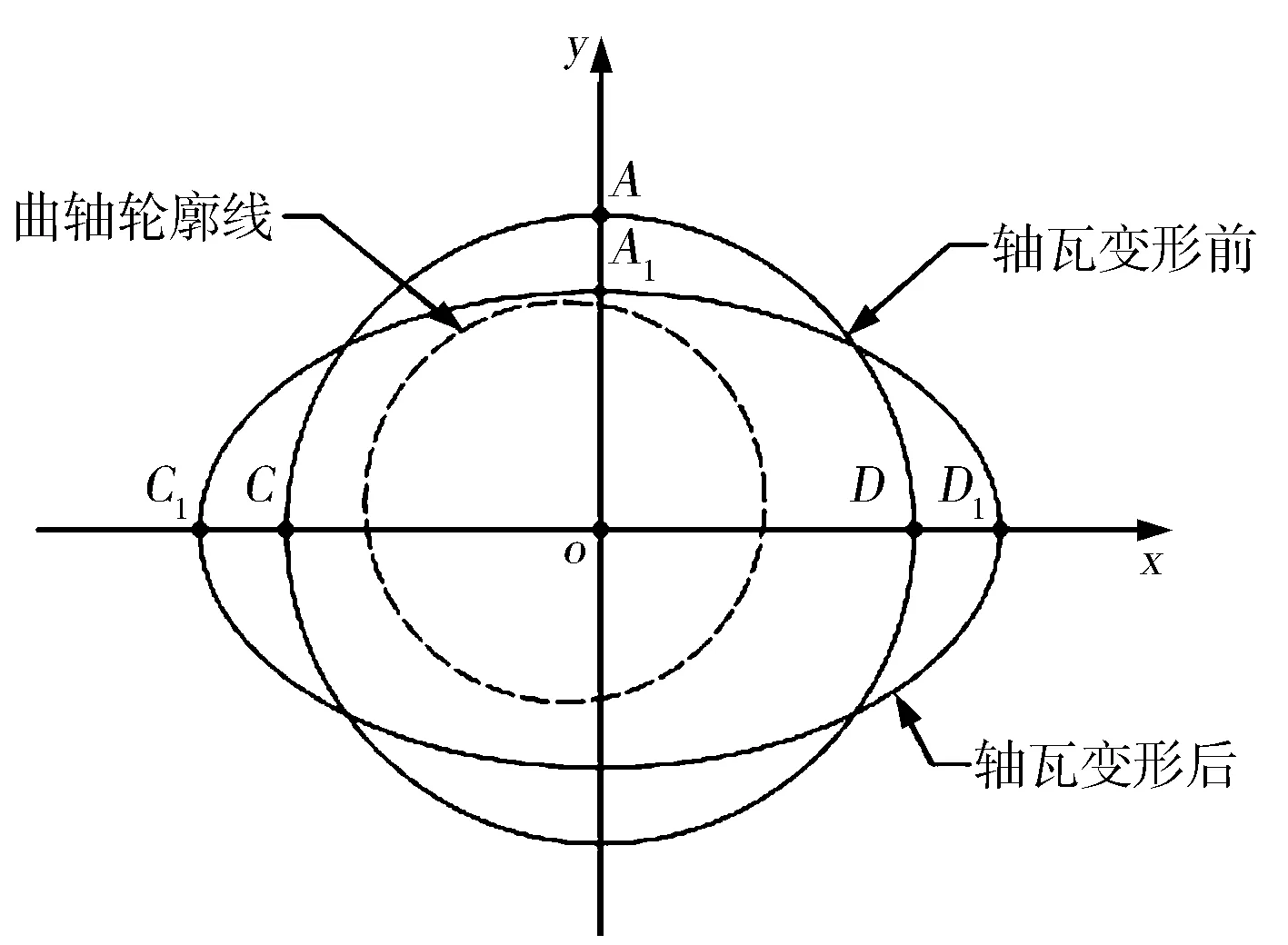
图5 主轴瓦“压扁”节点位置示意

根据前一节计算得到的主轴瓦变形后经过平移的节点坐标，若

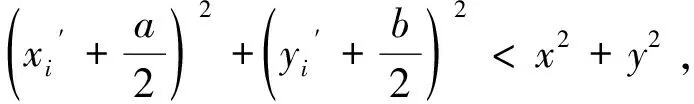
则认为该节点为“压扁”节点。式中，，为主轴瓦变形前节点的初始坐标。

2.2.4 主轴瓦“压扁”节点的径向配对

以“压扁”节点为元素构建节点集，获取该节点集内所有节点的编号。依据节点编号读取主轴瓦变形前的节点坐标。若主轴瓦变形前上轴瓦某节点与下轴瓦某节点之间的距离等于主轴瓦变形前的直径，则认为两节点变形后的节点与完成了径向配对。此时应分两种情况讨论。

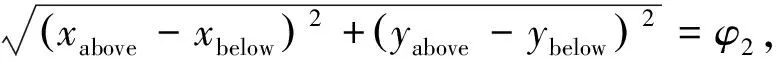
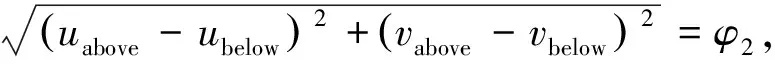
2.2.5 主轴瓦最大径向变形量的求解

以完成径向配对的节点和节点为例，二者在主轴瓦直径方向上的变形量分别为和，则两节点在主轴瓦直径方向上的变形量为Δ=+，如图6所示。由于和的数值不容易直观求解，可间接地通过主轴瓦变形后节点和之间的距离求解主轴瓦径向变形量Δ，即

Δ=-。

(10)

设主轴瓦变形后有对节点完成径向配对，则主轴瓦最大径向变形量可表示为max_Δ=max(Δ，Δ，Δ，…Δ)。

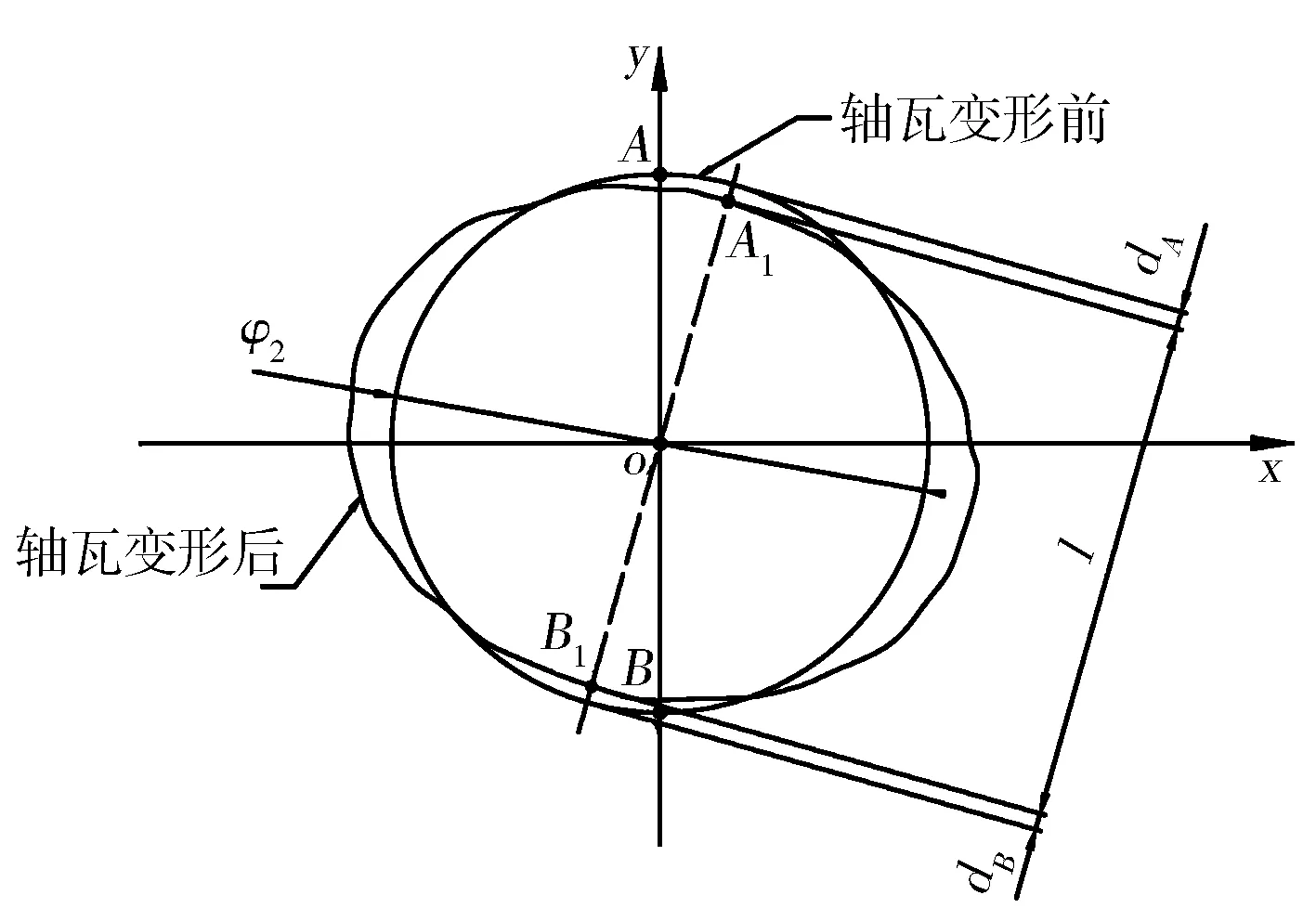
图6 主轴瓦变形前后位置关系示意

2.3 可行性分析

通过主轴瓦最大径向变形量的定义及计算方法可以看出，主轴瓦最大径向变形量可以量化地表征主轴承变形协调特性，即主轴瓦变形后与曲轴之间的协调运动关系。主轴瓦最大径向变形量越小，主轴承变形协调特性越优。设主轴瓦与曲轴的最小装配间隙为，为保证主轴瓦与曲轴的协调工作，则主轴瓦的最大径向变形量max_Δ应小于2。

对比文献[13]中单个主轴承变形协调特性的评价指标，主轴瓦最大径向变形量的计算效率明显更高。这是因为文献[13]中评价指标的计算包含了主轴瓦所有直径方向的变形量，而主轴瓦最大径向变形量的计算则通过预先识别“压扁”节点，在保证求解精度的情况下，只计算了部分“压扁”的径向变形量。

3 主轴瓦最大径向变形量的试验验证

主轴瓦最大径向变形量的验证试验主要采用INCOMETER轮廓测量仪对主轴瓦的变形量进行测量，该仪器的测量精度可以达到1 μm。测量前，需预设被测圆孔直径、夹持直径以及被测轴向截面坐标等参数。对被测圆孔各轴向截面的测量是通过丝杠轴上的马达驱动测针到指定位置的方式完成。根据被测表面的微小变化输出电子信号，经由控制电缆传递给控制箱，最终传递到计算机上。

由于轮廓测量仪对被测圆孔变形量的测量需要将测头深入到圆孔内，对于主轴承载荷工况下的主轴瓦最大径向变形量的测量有一定的难度，故本试验的测量目标为不装配曲轴的预紧工况下的主轴瓦最大径向变形量。

将轮廓测量仪的夹持爪夹持到最外侧隔板的主轴承孔内，尽量保证轮廓测量仪水平。以主轴瓦中间轴向截面的圆心作为坐标原点，选取轴向坐标分别为-20 mm，-10 mm，10 mm，20 mm的轴向截面作为测量对象，以丝杠轴上的马达驱动测头对预紧工况下第二隔板上被测截面的主轴瓦最大径向变形量进行测量，如图7所示。

图7 主轴瓦最大径向变形量测量示意

以坐标为-10 mm的主轴瓦轴向截面为例分析，共选取720个数据点，每0.5°绘制一次对应角度方向的变形量，预紧工况下主轴瓦仿真分析结果与试验测量结果对比见图8。从图8可以看出，主轴瓦试验测量轮廓线与仿真分析轮廓线的形状大致相同，二者相比理想轮廓线有一定的圆度误差。这是由于镗孔工艺技术无论是在仿真模拟中还是在实际生产加工中，都只能保证被加工圆孔在一定精度范围内为正圆，存在一定程度的圆度误差。

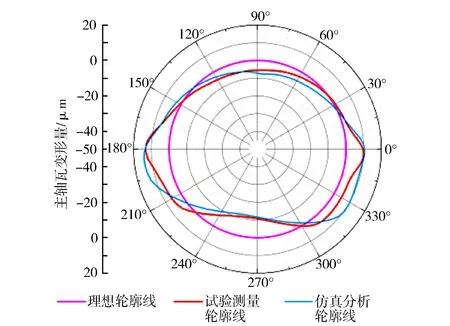
图8 预紧工况仿真与试验主轴瓦轮廓线对比

分别对4个主轴瓦最大径向变形量的考察截面进行测量，将测量数据与仿真结果进行对比，结果见图9。从图9可以看出，主轴瓦最大径向变形量的仿真结果与测量数据具有较好的一致性，各考察截面的仿真数据与试验数据的误差不超过7%，满足相对误差低于10%的计算要求，验证了所提出的主轴瓦最大径向变形量计算方法的正确性。

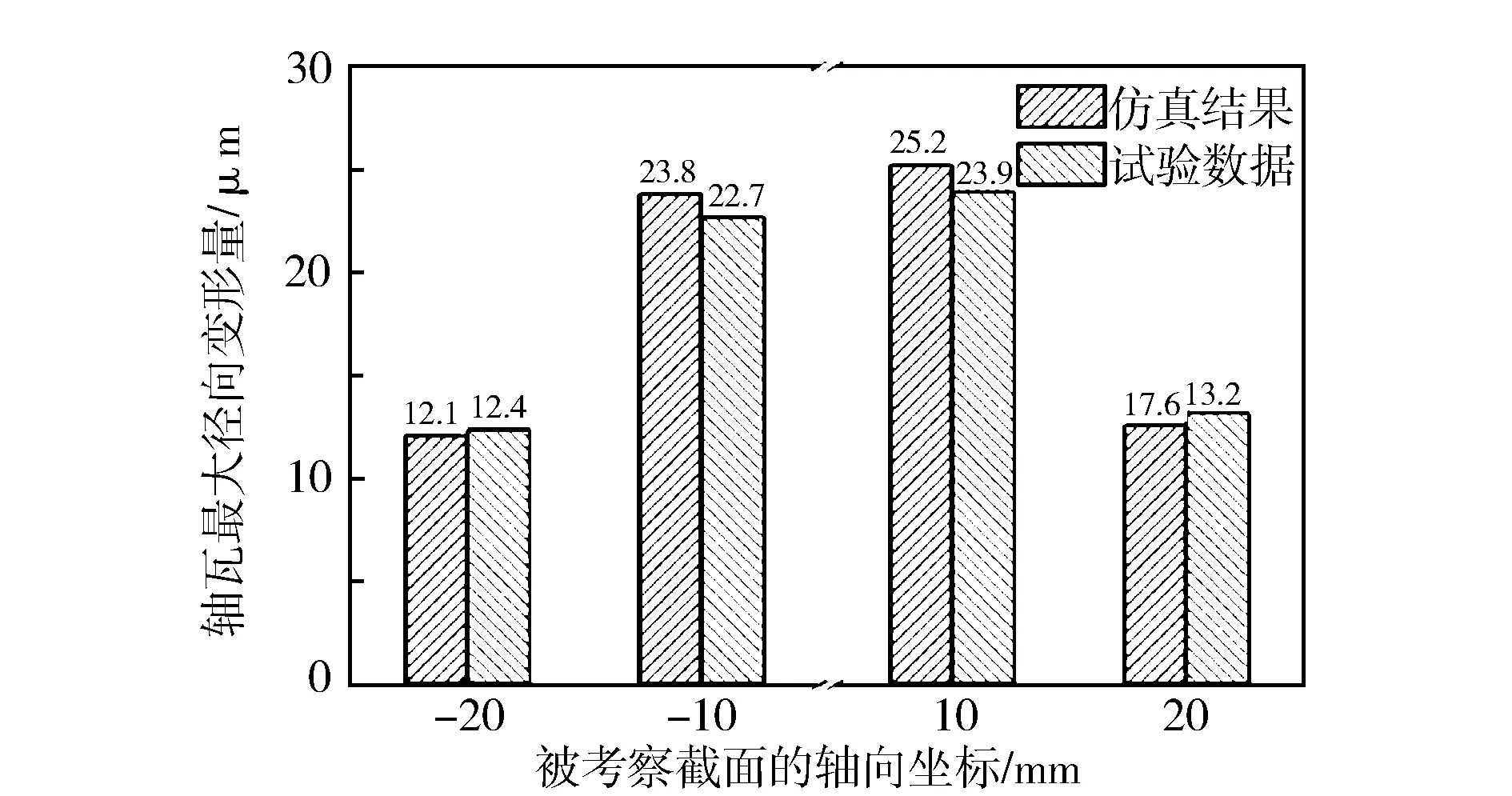
图9 主轴瓦最大径向变形量仿真与试验数据对比

4 主轴承变形协调特性的影响因素及影响规律分析

4.1 灵敏度分析

某V型主轴承组合结构单隔板模型结构示意见图10。在主轴承载荷一定的情况下，选取可能影响主轴承变形协调特性的设计参数，分别为机体侧壁加强筋厚度、机体隔板厚度、主轴承盖厚度、机体与主轴承盖装配侧隙、主轴瓦装配过盈量、竖拉螺栓预紧力与横、竖螺栓预紧力比例系数，设计七因素三水平的正交试验(如表2所示)。利用极差分析法获取不同设计参数对主轴瓦最大径向变形量的灵敏度，结果见图11。

从图11可以看出，横竖螺栓预紧力对主轴瓦最大径向变形量的灵敏度最高，结构装配参数包括机体与主轴承盖装配侧隙和主轴瓦装配过盈量二者对主轴瓦最大径向变形量的灵敏度次之，而结构尺寸参数对其灵敏度相对较小。

图10 主轴承组合结构示意

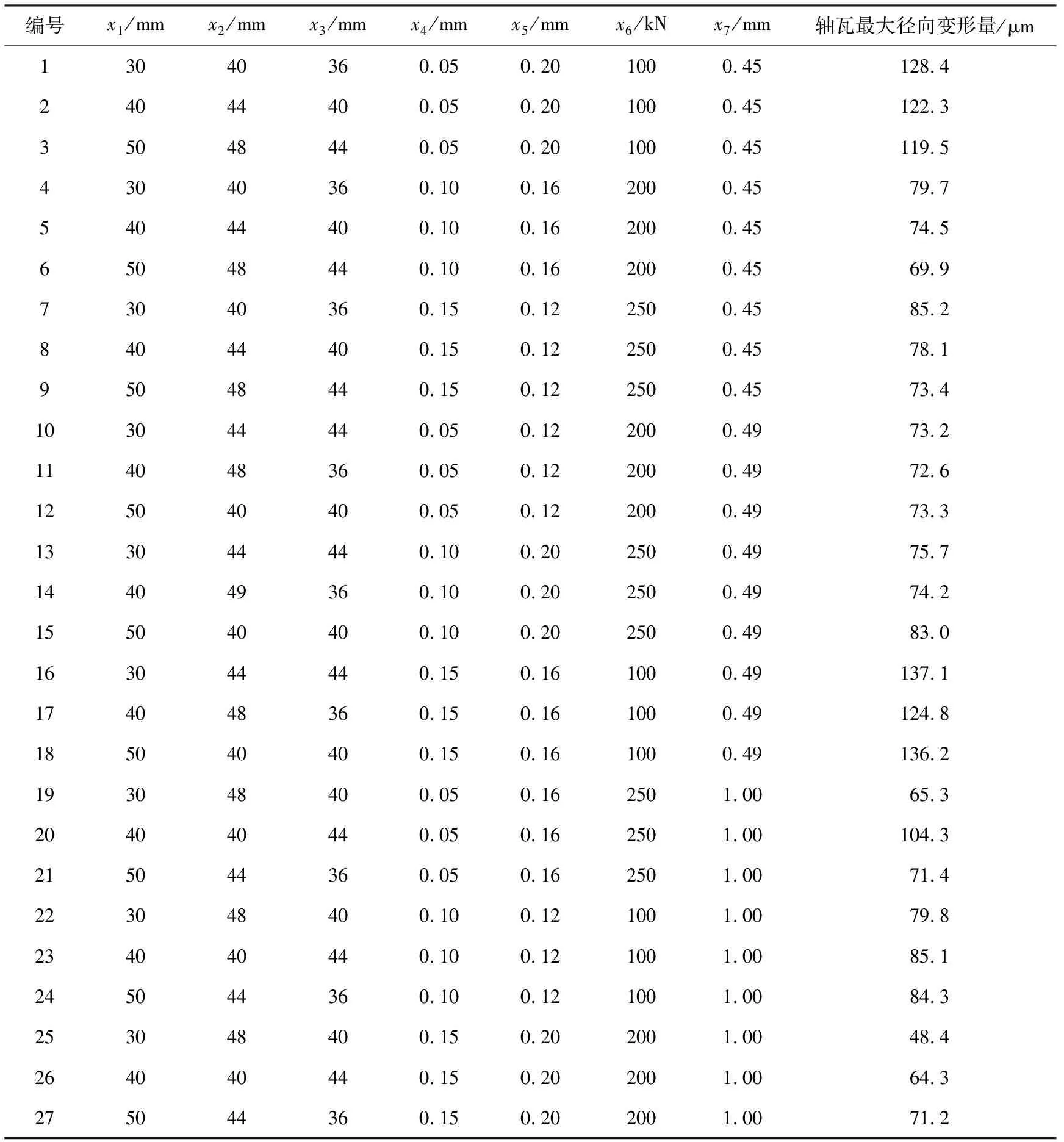
表2 七因素三水平正交试验表

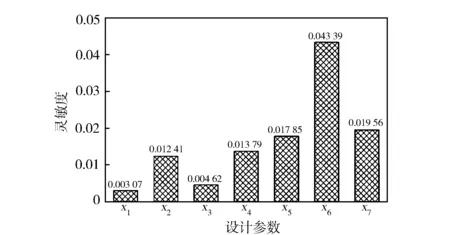
图11 设计参数对主轴瓦最大径向变形量的灵敏度

4.2 典型设计参数对主轴承变形协调特性的影响

基于设计参数对主轴瓦最大径向变形量的灵敏度分析，选取4个对主轴瓦最大径向变形量灵敏度较大的设计参数作为典型设计参数，分别为横竖螺栓预紧力、主轴瓦装配过盈量以及机体与主轴承盖装配侧隙。以坐标10 mm的轴向截面作为考察截面，在主轴承载荷保持不变的情况下，分析典型设计参数对主轴瓦最大径向变形量的影响规律。

4.2.1 竖拉螺栓预紧力对主轴承变形协调特性的影响

根据该柴油机主轴承组合结构设计要求，竖拉螺栓预紧力的最小值为100 kN，最大值为250 kN，分别进行主轴承载荷工况下主轴承组合结构有限元仿真分析并计算主轴瓦最大径向变形量，结果见图12。

分析图12数据可知，随着竖拉螺栓预紧力的增加，主轴瓦最大径向变形量逐渐降低，且其降幅逐渐趋于平缓。当竖拉螺栓预紧力为240 kN时，主轴瓦最大径向变形量降至最小。此后继续增加竖拉螺栓预紧力，主轴瓦最大径向变形量基本不发生变化。

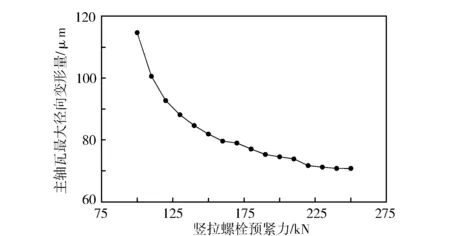
图12 竖拉螺栓预紧力对主轴瓦最大径向变形量的影响

分析这一规律的产生原因：增加竖拉螺栓预紧力会进一步压紧机体与主轴承盖，可以有效抑制主轴承载荷引起的主轴瓦失圆变形。当竖拉螺栓预紧力达到240 kN时，机体与主轴承盖整体保持紧密连接，相当于一个刚性部件，继续增加预紧力对主轴瓦径向变形的影响很小。

4.2.2 横拉螺栓预紧力对主轴承变形协调特性的影响

取横拉螺栓预紧力的最小值为20 kN，最大值为200 kN，对主轴承载荷工况下主轴承组合结构进行有限元仿真分析并计算主轴瓦最大径向变形量(见图13)。

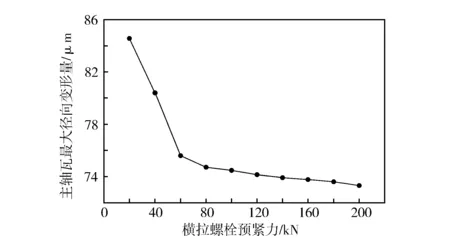
图13 横拉螺栓预紧力对主轴瓦最大径向变形量的影响

从图13可以看出，随着横拉螺栓预紧力的增加，主轴瓦最大径向变形量逐渐减小。当横拉螺栓预紧力小于80 kN时，主轴瓦最大径向变形量的递减趋势较为显著。之后持续增加横拉螺栓预紧力，主轴瓦最大径向变形量的递减趋势逐渐平缓。

横拉螺栓连接的目的是使机体与轴承盖在横向紧密贴合，当承受主轴承横向载荷时，机体与主轴承盖间具备足够的横向夹紧力，以确保主轴承的可靠连接和正常工作。机体与主轴承盖的横向夹紧力持续增加，使机体与主轴承盖在横向几乎被耦合成一个刚性部件，此时横拉螺栓预紧力对主轴瓦最大径向变形量的灵敏度降低。

4.2.3 主轴瓦装配过盈量对主轴承变形协调特性的影响

根据该柴油机主轴瓦许用装配公差范围，装配过盈量最大值取0.2 mm，最小值取0.12 mm，建立主轴承载荷工况下不同过盈量的主轴承组合结构有限元模型并进行仿真分析，计算考察截面的主轴瓦最大径向变形量，结果见图14。

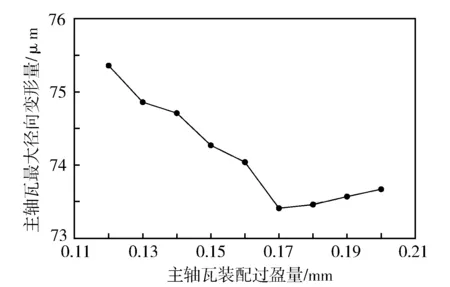
图14 主轴瓦装配过盈量对主轴瓦最大径向变形量的影响

从图14可知，随着主轴瓦过盈量的增加，主轴瓦最大径向变形量呈逐渐递减的趋势。当过盈量为0.17 mm时，最大径向变形量处于最小值76.4 μm。当过盈量大于0.17 mm时，主轴瓦最大径向变形量呈缓慢递增的趋势。

分析产生这一现象的原因：过盈量越大表明主轴瓦与主轴承孔间周向的过盈载荷越大。当过盈量较小时，增加过盈量使主轴瓦与主轴承孔更加紧密贴合，可以有效抑制主轴承载荷引起的主轴承变形。当过盈量大于0.17 mm时，继续增加过盈量会使主轴瓦背压过大，极有可能超过了主轴瓦材料本身的屈服极限而产生变形，故变形加剧主要是由冗余的主轴瓦过盈载荷引起的。

4.2.4 机体与主轴承盖装配侧隙对主轴承变形协调特性的影响

根据主轴承组合结构机体与主轴承盖侧壁装配公差的许用要求，机体与主轴承盖装配侧隙的最小值取0.05 mm，最大值取0.15 mm，分别进行主轴承组合结构有限元仿真分析并计算考察截面的最大径向变形量，结果如图15所示。

由图15可知，随着装配侧隙的增加，主轴瓦最大径向变形量逐渐递增。分析这一现象产生的原因：横拉螺栓载荷会使机体与主轴承盖紧密贴合，机体与主轴承盖的装配侧隙最终会由于横拉螺栓的紧固作用而消失，在这个过程中必然会造成机体的变形。侧隙增大会导致机体主轴承孔局部的变形增加，进而对主轴承的变形产生影响。

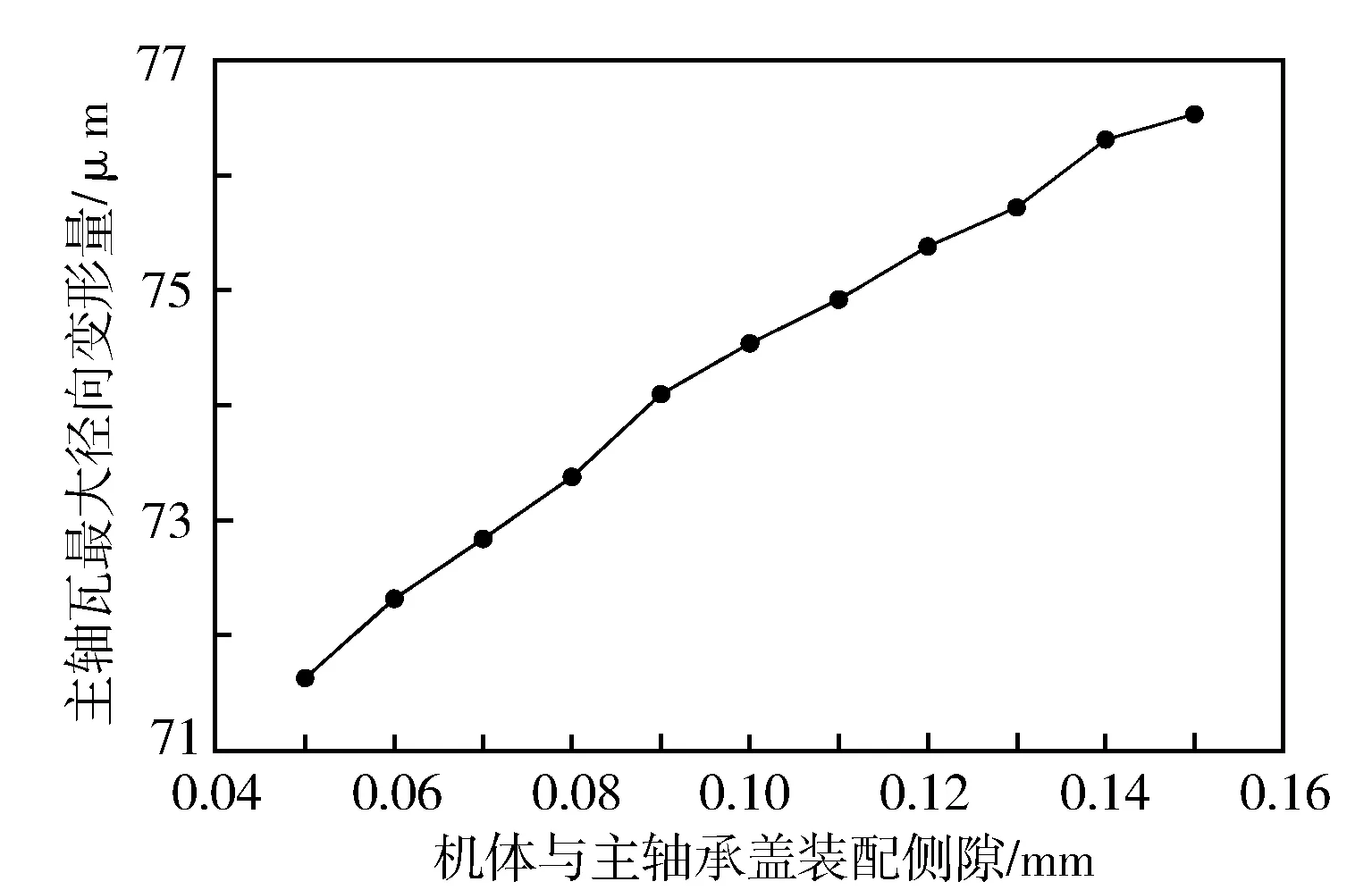
图15 机体与主轴承盖装配侧隙对主轴瓦最大径向变形量的影响规律

5 结论

a) 提出的以主轴瓦最大径向变形量评判主轴承变形协调特性的评价方法具备很高的可行性，该评价方法计算效率高且能够量化地表征主轴瓦变形后与曲轴之间的协调运动关系；

b) 预紧工况下，采用本研究中的主轴瓦最大径向变形量数值计算方法得到的仿真计算结果与试验测量数据之间的相对误差在7%以内，表明提出的主轴瓦最大径向变形量数值计算方法的正确性；

c) 主轴承载荷一定的情况下，随着横竖螺栓预紧力的增加，主轴瓦最大径向变形量呈逐渐减小的趋势；当螺栓预紧力增加到一定程度时，机体与主轴承盖紧密连接几乎耦合成一个刚性部件，此时螺栓预紧力对主轴瓦最大径向变形量的敏感度较低；随着过盈量增加，主轴瓦最大径向变形量呈逐渐减小的趋势；随着机体与主轴承盖装配侧隙的增加，主轴瓦最大径向变形量几乎呈线性递增的趋势。