基于全局帕德逼近的米塔-列夫勒函数及其导数的数值算法

方宇孟，袁 晓，谢雨婧

（四川大学 电子信息学院，成都 610065）

0 引 言

在经典的整数阶微分方程理论中，指数函数e（∈ℝ）起着非常重要的作用，且是微分方程

的解：（）e。

复变量（i）的整函数—解析指数函数e的幂级数展开为：

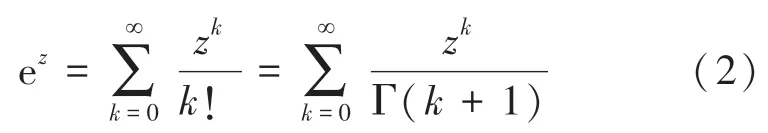
e的任意有限阶导数等于自身，这一特性对傅里叶变换、拉普拉斯变换和变换意义重大。

1903年，米塔-列夫勒提出单参数米塔-列夫勒函数：

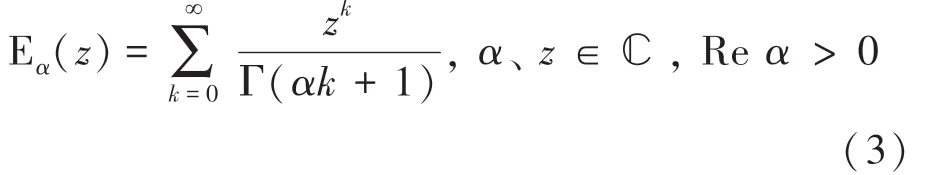
其中，E（）是指数函数的单参量广义化结果。

1905年，Wiman提出双参数米塔-列夫勒函数：

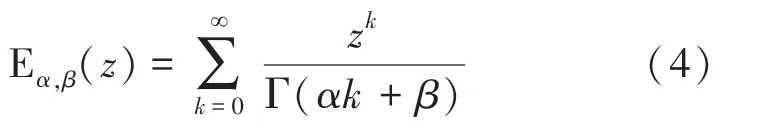
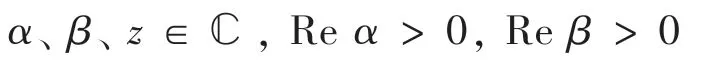
显然有：EE。

1971年，Prabhakar提出三参数米塔-列夫勒函数：

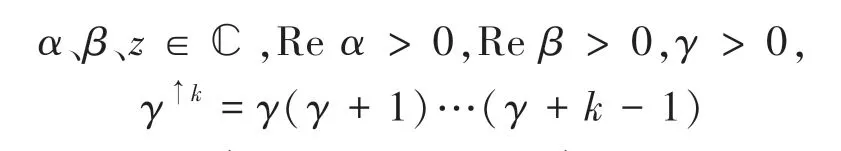
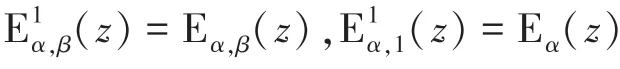
米塔-列夫勒函数在分数阶系统中的重要性如同指数函数在整数阶系统中的重要性。E（）称为分数微积分的女王函数（the Queen Function of Fractional Calculus）。米塔-列夫勒函数类可用于表示分数阶微积分方程的解，比如：第二类阿贝尔积分方程，含有黎曼-刘维尔分数导数的微分方程等，还可应用于许多现代分数阶模型，比如：神经网络中的信息处理、聚合物网络中的黏弹性、分子输运、热传导、信号处理和反常扩散。

米塔-列夫勒函数广泛应用在各种研究领域与工程应用之中，因此有必要研究米塔-列夫勒函数的快速有效高精度算法。2002年，Gorenflo等人提出分区算法，采用泰勒级数、积分表达和渐进级数三种方法来计算米塔-列夫勒函数，但算法存在计算错误。2015年，Garrappa等人基于米塔-列夫勒函数的拉普拉斯变换，提出最优抛物线围线算法。2018年，Garrappa等人在文献［17］中研究了带矩阵参数的米塔-列夫勒函数的数值计算。2020年，Saenko提出一种新的积分算法，将米塔-列夫勒函数的积分表示成实部和虚部的和且每部分只依赖实变量和实参数，但算法存在一定局限性。

除了以上提到的算法，研究者们还将帕德逼近法应用于米塔-列夫勒函数的数值计算。帕德逼近（Padéapproximation）是法国数学家亨利·帕德提出的有理多项式近似法，往往比截断的泰勒级数准确。2007年，Starovoitov等人利用帕德逼近法研究了米塔-列夫勒函数在｛≤1｝范围内的计算。文献［20］和文献［21］基于帕德逼近法研究了米塔-列夫勒函数E（-x）（0）的上下边界。

2003年，Winitzki在帕德逼近的基础上提出全局帕德逼近（global Padéapproximation），构造了超越函数的一致逼近。2005年，Diethelm等人提供了米塔-列夫勒函数E（-x）（01）的有理逼近系数表，在{∈［01，15］}范围内具有良好的计算精度。2011年，Atkinson等人利用全局帕德逼近法实现米塔-列夫勒函数E（）在{01，0}范围内的二阶逼近，但二阶逼近的效果差，为了进一步提高计算精度，需要扩展到更高阶逼近。

在前人研究基础上，本文将全局帕德逼近法应用于双参数米塔-列夫勒函数E（）及其任意阶导数的数值计算，实现了10阶逼近，计算精度可达1×10%。经理论分析和仿真实验，证明了该算法的运算有效性和可行性。

1 米塔-列夫勒函数的基本性质

米塔-列夫勒函数最主要的性质有4种：积分、微分、渐进、拉普拉斯变换。这些性质不仅有助于求解分数阶微积分方程，而且在实际的工程应用中具有重要意义，比如：Bagley-Torvik方程的数值求解，分数阶被控系统和分数阶PD控制器系统中表示单位阶跃响应，电介质的分数阶松弛方程的求解等。

1.1 米塔-列夫勒函数的积分

对双参数米塔-列夫勒函数（4）逐项积分得：

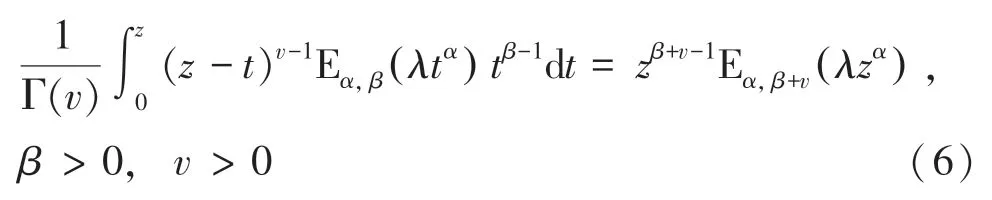
其中，当＝1时，得到式（6）的一个特例：

Erdélyi等人和Džrbašyan等人研究了米塔-列夫勒函数沿汉克尔环的反常积分形式，得到定理1。

设02且∈ℂ，则对任意0与，满足π2≤min｛π，π｝时，有：

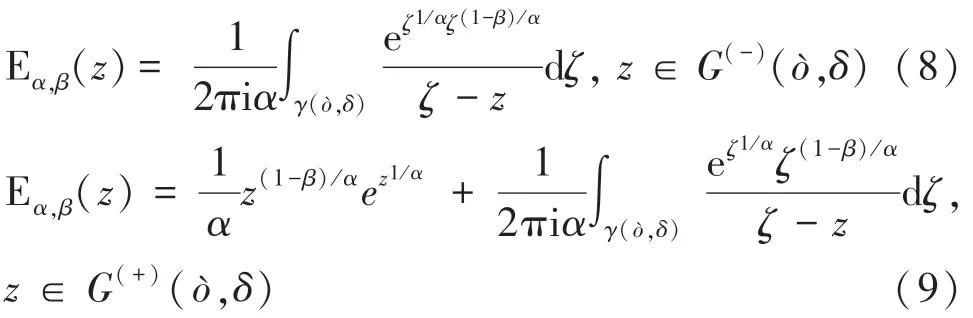
其中，积分围线（，）如图1所示，由2条射线S（arg，≥）和S（arg，≥）以及一个圆弧C（0，）（，≤arg≤）组成。积分围线左侧区域是（，），右侧区域是（，）。表示圆弧G的半径，表示积分变量的角度。

图1 积分围线γ（ò，δ）［14］Fig.1 Integral contourγ（ò，δ）［14］

1.2 米塔-列夫勒函数的微分

对双参数米塔-列夫勒函数E（）逐次求导可得阶导数公式：

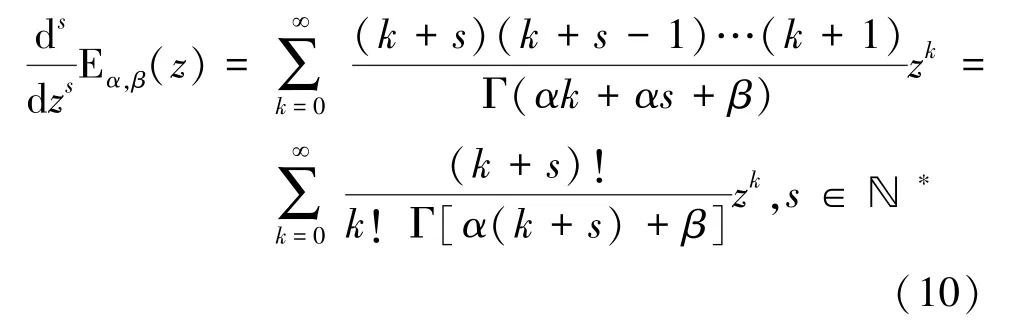
另外，文献［5］中给出阶导数公式：

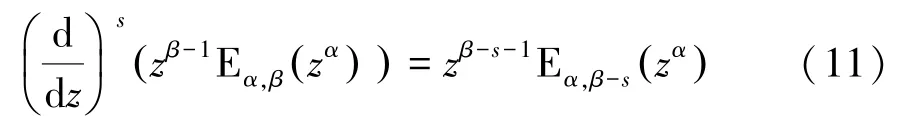
1.3 米塔-列夫勒函数的渐进展开

利用式（8）和式（9）的积分表达得到米塔-列夫勒函数在复平面上的渐进表达。

对于02、∈ℂ、∈ℕ，当argmin｛π，π｝时，有渐进展开式：

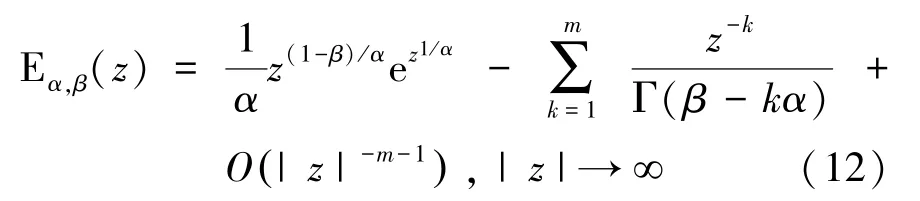
当01，πargπ时，有渐进展开式：

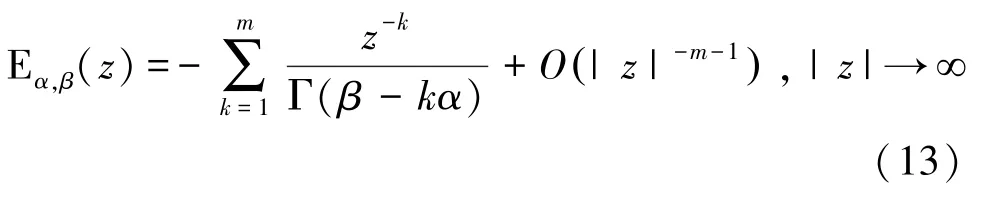
1.4 米塔-列夫勒函数的拉普拉斯变换

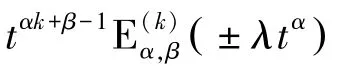
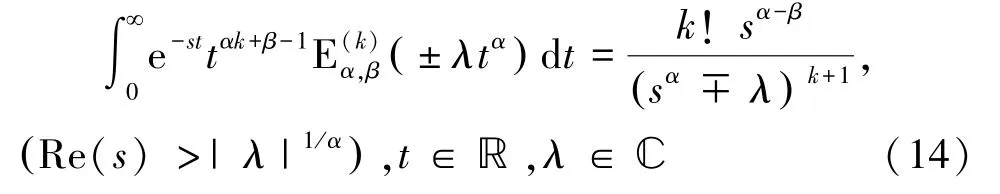
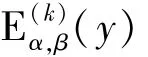
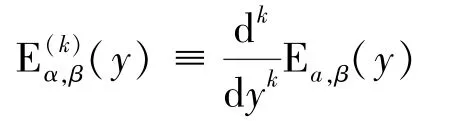
2 米塔-列夫勒函数的数值算法

2.1 分区算法

Gorenflo等人提出分区算法，用泰勒级数、积分表达和渐进级数计算复平面上不同区域的米塔-列夫勒函数。Seybold等人在Gorenflo等人的基础上做了改进，消除了变量靠近积分围线时的不稳定现象。

对于0、∈ℝ，分区算法能够计算复平面上任意米塔-列夫勒函数E（）的值。对复平面上的不同取值，采用不同的数值计算方法，以获得最佳的稳定性和精度。基本思路是：当0≤1、∈ℝ时，≤则用泰勒级数（式（4））计算；≥则用渐进级数（式（17）和式（18））计算；则用积分表达（式（8）和式（9））计算。其中，表示采用泰勒级数方法的区域半径上限值，表示采用渐进级数方法的区域半径下限值。当1时，用递归公式将其转为0≤1的情形再计算：

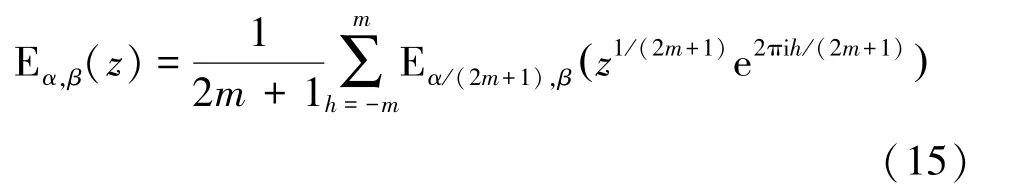
其中，∈ℝ，∈ℂ；［（1）2］1；［］为不超过的最大整数。

然而，分区算法存在一定缺陷。Popolizio等人指出分区算法存在计算错误。Saenko证明了定理1有误，当∈（，）时，积分表达式正确；当∈（，）时，积分表达式错误。指出分区算法因使用了定理1导致∈（，）产生计算错误。

2.2 最优抛物线围线算法

Garrappa等人提出最优抛物线围线算法，在复平面上选择计算量和误差都最小的区域，对米塔-列夫勒函数进行拉普拉斯反演计算。适用范围：0，∈ℝ，∈ℂ。核心计算公式为：

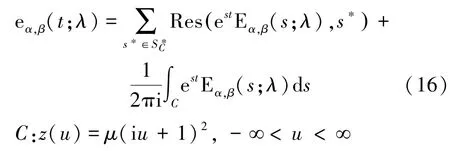
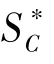
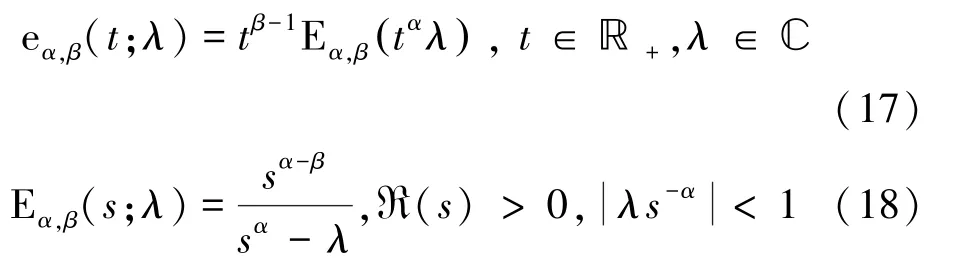
2.3 全局帕德逼近算法

2.3.1 全局帕德逼近

帕德逼近是从幂级数出发获得有理逼近的一种简洁且有效的方法。其基本思想是对一个给定形式的幂级数构造一个有理函数，使该有理函数的泰勒展开尽可能与原来的幂级数吻合。这种方法克服了用多项式逼近大扰度函数效果不理想以及用幂级数（如泰勒级数）逼近函数收敛性太差等缺点。

设函数（）∈［，］，1，如果有理函数R（）可展开为：

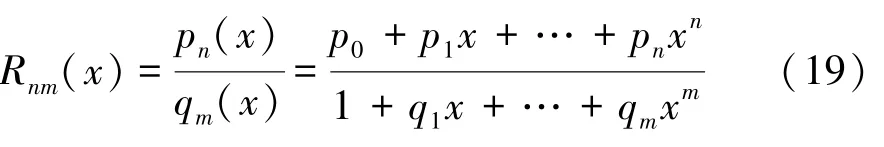
其中，p（）和q（）互质，且满足条件：

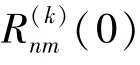
Winitzki对式（19）进行改进，提出全局帕德逼近形式：

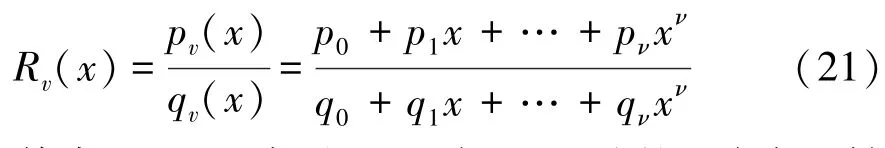
其中，R（）表示（）在0处的阶全局帕德逼近。

2.3.2 米塔-列夫勒函数的全局帕德逼近

Winitzki利用全局帕德逼近法实现了椭圆函数、误差函数、贝塞尔函数和艾里函数的有理逼近。全局帕德逼近法主要是利用初等函数的泰勒级数和超越函数的渐近级数实现计算。当｛0≤1，≥｝时，米塔-列夫勒函数E（）在［0，∞）上是单调且有限的，有E（∞）0。根据Winitzki的思想，可将全局帕德逼近法扩展到双参数米塔-列夫勒函数E（）(≥0)的数值计算之中，分2种情况计算：｛0≤1，｝和｛01｝。

（1）情况一：｛0≤1，｝

根据双参数米塔-列夫勒函数定义式（4）得Γ（）E（）的泰勒级数和渐进级数：

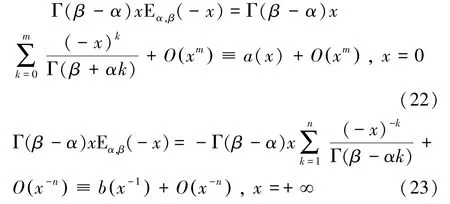
其中，加权项Γ（）保证渐近级数（23）的第一项系数为1。

对式（22）和式（23）取全局帕德近似：

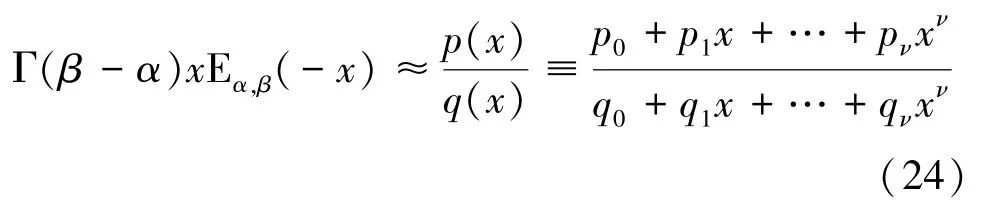
其中，∈ℕ，表示全局帕德逼近的阶数。而当＝∞时，式（24）右边多项式的值为p／q，且可令p＝q＝1。未知系数p和q（0，1，…，1）可由线性方程组求出：

其中，当为奇数时，该非齐次线性方程组存在唯一解。当≈时，式（24）的近似效果最好。

根据文献［34］提及的米塔-列夫勒函数的2阶逼近多项式，对式（22）和式（23）截断为1阶和2阶，令式（24）中2，得到：

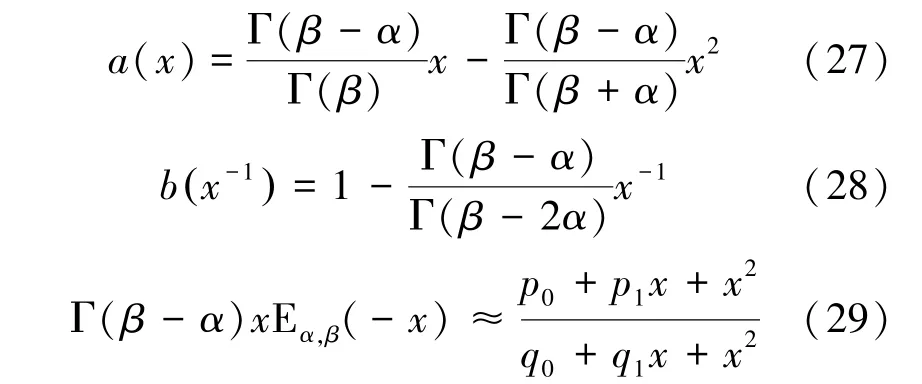
将式（27）～式（29）代入式（25）和（26）中，解出系数：

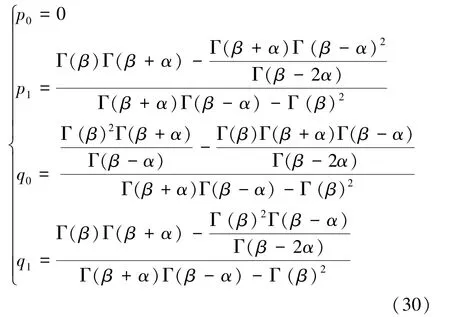
将式（30）代入式（29）中得到E（）的2阶全局帕德逼近式：

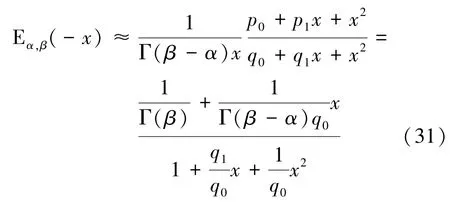
同理，若要计算E（）的阶逼近，对式（22）和式（23）截断为1阶和阶，得：

将式（32）～式（34）代入式（25）和式（26）中，求解式（34）中的系数p和q（0，1，…，1）。但随着式（34）中等号右边的多项式阶数的增大，系数p和q的表达式中的Γ代数项也会增多。当阶数7时，系数p和q的表达式中的Γ代数项超过1 000个。当式（32）～式（34）中多项式阶数较大，难以手算求解，可借助Matlab软件中的（）函数求解代数方程，得到系数p和q的表达式。

系数p和q的表达式只跟参数和有关，因此可根据参数和的取值，预先计算系数p和q的值并存入矩阵中，以优化精度、计算时间和系统内存。

经过Matlab软件求解可知，仅0，～p（2）的表达式太过复杂不便于表示，由式（34）得E（）的阶全局帕德逼近式：

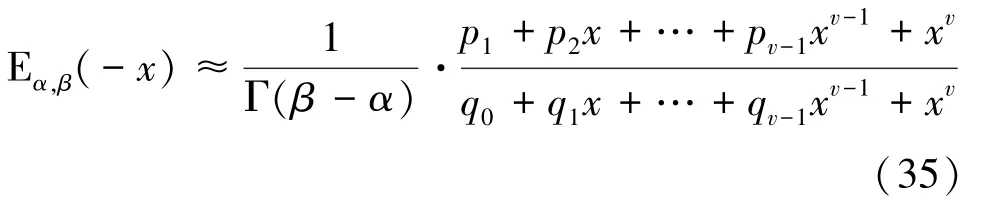
（2）情况二：｛01｝

当时，米塔-列夫勒函数E（）有泰勒级数和渐进级数：

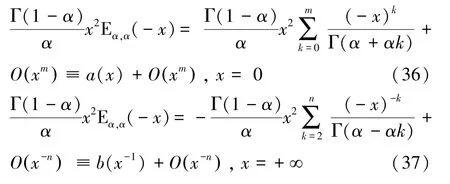
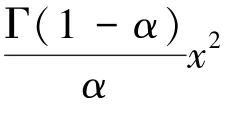
基于情况一的方法，解出情况二时E（）的2阶全局帕德逼近式：

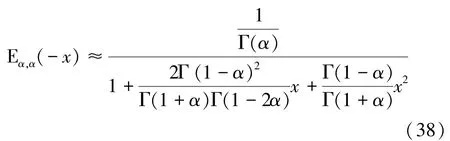
经Matlab软件求解可知，仅0，得E（）的阶全局帕德逼近式：

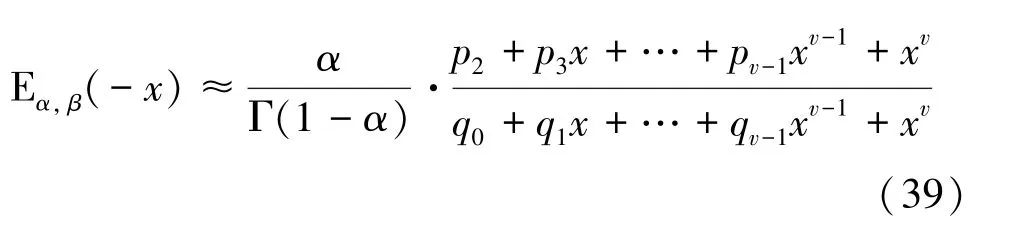
2.4 仿真结果及分析

为研究全局帕德逼近算法对米塔-列夫勒函数的逼近效果，需要考虑的影响因素有：逼近阶数和参数。可将全局帕德逼近算法、分区算法和最优抛物线围线算法做比较，综合分析全局帕德逼近算法的逼近性能。

相对误差函数的数学定义为：

米塔-列夫勒函数E（）和E（）的解析为：

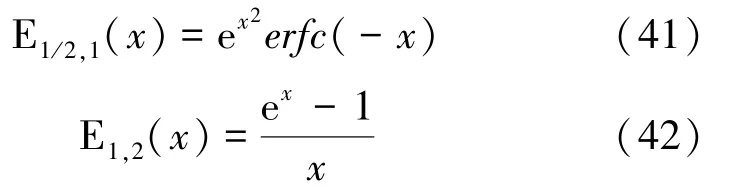
其中，误差函数（）：

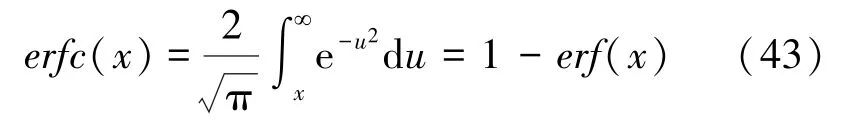
在此基础上，拟对仿真结果进行剖析分述如下。

（1）分区算法、最优抛物线围线算法和全局帕德逼近算法的比较。这里利用分区算法、最优抛物线围线算法、全局帕德逼近算法和解析式（42）绘制米塔-列夫勒函数E（）曲线，并绘制3种算法与解析解之间的相对误差曲线，如图2所示。观察到，最优抛物线围线算法在整个区间内的计算精度最好，误差稳定在110数量级。分区算法的误差在区间（10，15）内急剧增大，最高达530.6%，在其他区间的计算精度很好，甚至在区间（14，1 000）内的相对误差为0。全局帕德逼近算法的10阶逼近的最大误差为110610，而在区间（150，1 000）内的误差稳定在110数量级。

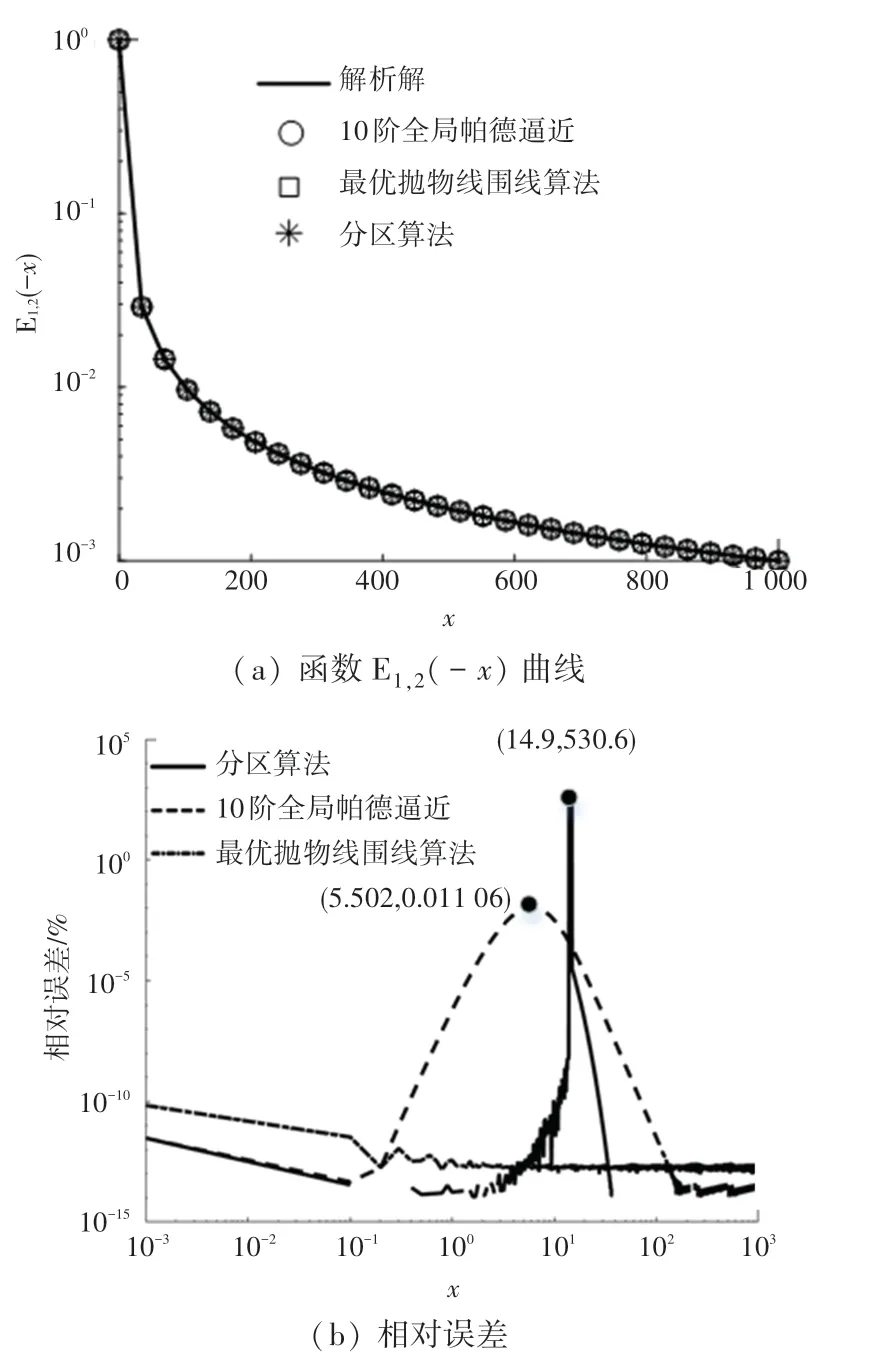
图2 α＝1，β＝2，比较分区算法、最优抛物线围线算法和全局帕德逼近算法Fig.2 Comparing the partitioning algorithm，the optimal parabolic contour algorithm and the global Padé approximation algorithm forα＝1，β＝2

文献［31］提到分区算法因使用了错误的积分表达导致∈（，）时产生计算错误，因此在区间（10，15）内的误差非常大。由此看出，分区算法的计算准确性不如全局帕德逼近算法和最优抛物线围线算法。最优抛物线围线算法的计算精度高且稳定，可用于下文验证全局帕德逼近算法的逼近性能。

（2）全局帕德逼近算法的逼近性能。为探究逼近阶数对逼近效果的影响，可绘制不同阶数下全局帕德逼近的相对误差曲线，如图3所示。当｛01｝时，将全局帕德逼近算法和最优抛物线围线算法的计算结果相比较，如图3（a）所示。当｛0≤1，｝时，将全局帕德逼近算法和解析式（41）～（42）的计算结果相比较，如图3（b）和图3（c）所示。图3展示了逼近阶数2，4，6，8，10时的全局帕德逼近的相对误差。

为探究对逼近效果的影响，固定的值，绘制在不同取值时的相对误差曲线，如图4所示。其中，纵坐标表示全局帕德逼近算法和最优抛物线围线算法之间的相对误差。

当逼近阶数2时，难以手算求解系数p和q，可借助Matlab软件求解。当05、1时，对应的10阶全局帕德逼近系数p和q（0，1，…，9）的值见表1和表2。

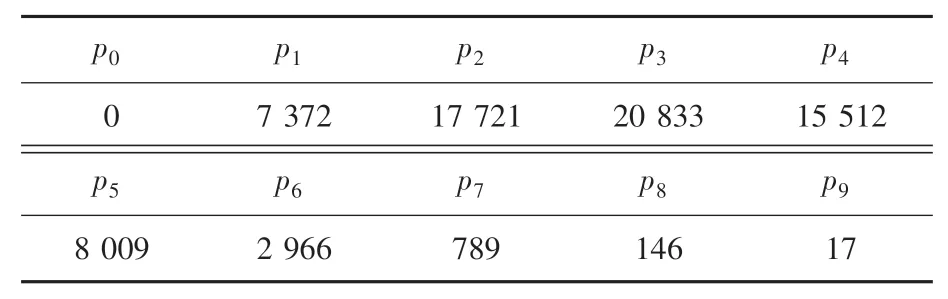
表1 系数pi（i＝0，1，…，9）的值（α＝0.5，β＝1，v＝10）Tab.1 The value of the coefficient pi（i＝0，1，…，9）（α＝0.5，β＝1，v＝10）

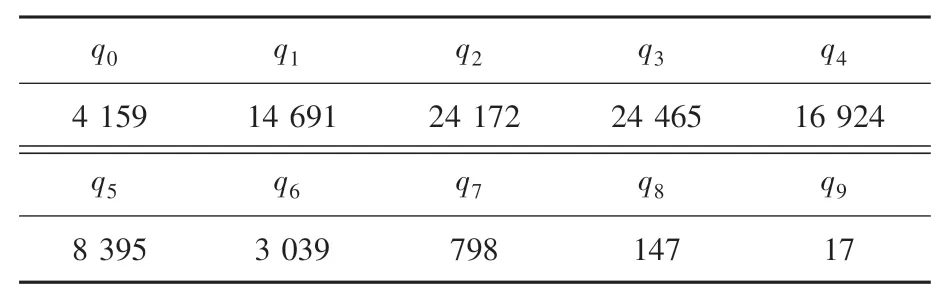
表2 系数qi（i＝0，1，…，9）的值（α＝0.5，β＝1，v＝10）Tab.2 The value of the coefficient qi（i＝0，1，…，9）（α＝0.5，β＝1，v＝10）

观察图3和图4，可得结论：

图3 v对逼近效果的影响Fig.3 The effect of v on the approximation

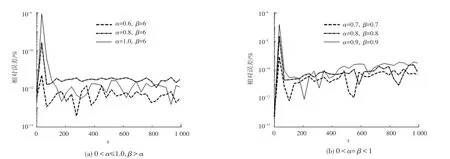
图4 α对逼近效果的影响Fig.4 The effect ofαon the approximation

（1）全局帕德逼近算法能在任意逼近阶数下计算米塔-列夫勒函数E（），逼近阶数越高，误差越小，逼近效果越好。当逼近阶数10时，已提供了足够的计算精度，和最优抛物线围线算法相当，计算精度可达110。

（2）当的值固定时，的值越接近1，在区间（0，200）内的误差越大且存在一个最大误差，而误差在区间（200，∞）内稳定在低水平。

（3）当取值很小或很大时，全局帕德逼近算法的优势尤其明显，计算精度很高。取中间值时存在最大误差，可提高逼近阶数来降低误差。

3 米塔-列夫勒函数导数的全局帕德逼近

3.1 任意阶导数的全局帕德逼近

将全局帕德逼近算法扩展到米塔-列夫勒函数任意阶导数dE（）d（）（0，∈ℕ）的数值计算，与2.3节方法相同，分2种情况：｛0≤1，｝和｛01｝。为了便于计算，取，则任意阶导数表示为：

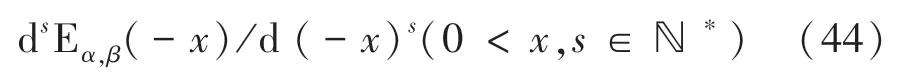
表3总结了双参数米塔-列夫勒函数任意阶导数的全局帕德逼近，列出了参数适用范围、核心计算公式（泰勒级数和渐进级数）以及阶全局帕德逼近式。其中，表示米塔列夫勒函数的导数阶数，表示全局帕德逼近算法的逼近阶数，p和q表示全局帕德逼近式的系数。得到以下几点：

表3 双参数米塔-列夫勒函数任意阶导数的全局帕德逼近Tab.3 Global Padéapproximation for any derivative of two-parameter Mittag-Leffler functions

（1）阶导数的泰勒级数和渐进级数的加权项：

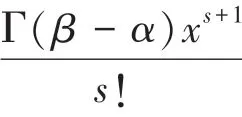
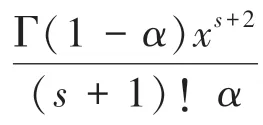
（2）经Matlab软件编程求解，可知阶导数的阶全局帕德逼近系数p（0，1，…，1）：

当{0≤1，}时：…＝p＝p＝0；

当｛01｝时：…＝p＝p0。

（3）当阶数2时，可直接手算解出系数p和q的表达式。当阶数2时，难以手算求解，系数p和q（0，1…，1）（除p＝0之外）的表达式随着的增大而越复杂，此时可借助Matlab软件求解。系数p和q的表达式只与参数和有关，因此可根据参数和的取值，预先计算系数p和q的值并存入矩阵中，以优化精度、计算时间和系统内存。

3.2 仿真结果及分析

当{0≤1，≤，0}时，通过Matlab 软件可求解任意阶导数的全局帕德逼近式。为了探究全局帕德逼近算法的准确性，不妨将全局帕德逼近式的计算结果与文献［35］中_（）函数的计算结果相比较，仿真结果如图5～图8所示。_（）函数能求解1到4参数（、、、）的米塔-列夫勒函数及其导数，是目前唯一能够求解任意阶米塔-列夫勒函数导数的可用代码。

为探究导数阶数和逼近阶数对逼近效果的影响，绘制E（）的一阶、二阶、三阶导数在不同逼近阶数下的相对误差曲线，可见图5～图7。

图7 α＝0.47，β＝0.47，x∈［0，3］Fig.7 α＝0.47，β＝0.47，x∈［0，3］

为了探究和取值向1趋近时的逼近效果，这里取｛05，07，09｝，绘制dE（）d（）的10阶全局帕德逼近曲线、_（）函数曲线以及两者的相对误差曲线，可见图8。

观察图5～图8，得到结论：

（1）全局帕德逼近算法的逼近阶数越高，误差越小，逼近效果越好。

（2）米塔-列夫勒函数的导数阶数越高，达到相同逼近效果所需的逼近阶数越高。图5中，一阶导数的四阶逼近的相对误差大小和三阶导数的六阶逼近的差不多。

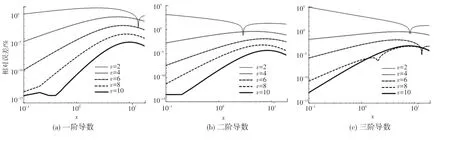
图5 α＝1，β＝8，x∈［0，20］Fig.5 α＝1，β＝8，x∈［0，20］

（3）当{01}时，和取值越接近于1，逼近效果越差。图8中，在相同条件下，和取值越大，相对误差越大。当05时，最大相对误差低于110。当09时，最大相对误差超过1×10%。

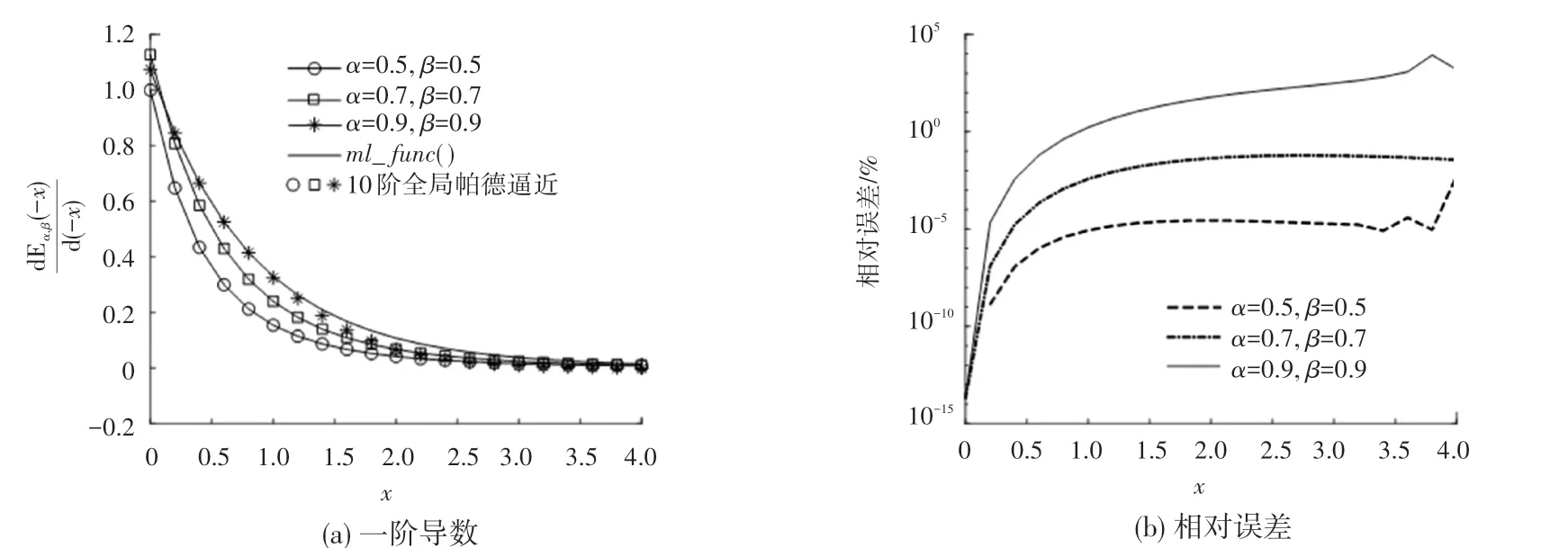
图8 α和β对逼近效果的影响Fig.8 The effect ofαandβon the approximation

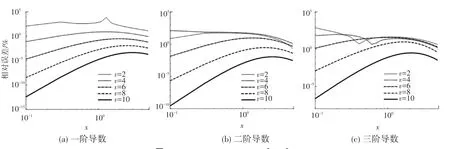
图6 α＝0.65，β＝0.95，x∈［0，5］Fig.6 α＝0.65，β＝0.95，x∈［0，5］

4 结束语

米塔-列夫勒函数类的表示、快速有效高精度计算、显示、应用是近年来的研究热点。本文基于全局帕德逼近技术构造双参数米塔-列夫勒函数E（）及其任意阶导数dE（）d（）（∈ℕ）的数值算法，从泰勒级数和渐进级数出发实现高阶全局帕德逼近。根据和的取值，分2种情况计算：｛0≤1，｝和｛01｝，理论分析并求解全局帕德逼近式。通过大量仿真实验，证明了全局帕德逼近算法的逼近性能优越，数值求解结果稳定可靠。逼近阶数越高，逼近效果越好，10阶逼近的计算精度可达110；导数阶数越高，达到指定精度所需的逼近阶数越高。