图形化编程环境下建模方式对学生计算思维与编程行为的影响研究

杨刚 张银荣 徐佳艳 曾群芳 陈赛

[摘   要] 计算思维改变学习者学习其他事物的方式。因此，计算思维的培养成了当前我国中小学编程教育研究的热点问题之一。研究以目前中小学开展编程教育存在的问题为出发点，从理论上探讨了计算思维、计算建模的重要性及其两者的关系。在此基础上构建了计算教学法模式，以这一模式为研究载体，对使用不同建模方式的组别开展编程学习活动，并借助析因分析法、T检验、滞后序列分析法等研究方法对所获得的实验数据进行处理与分析。结果表明：相比于开放式建模方式，支架式建模方式更能够提升学生计算思维的成绩，但是实验组与对照组之间的自我效能感没有显著性差异。另外，在学习行为分析中出现的一些共性问题值得教育研究工作者和一线教师深入思考。

[关键词] 建模方式; 计算思维; 图形化编程

[中图分类号] G434            [文献标志码] A

[作者简介] 杨刚（1979—），男，湖南怀化人。副教授，博士，主要从事数字化学习、信息技术教学研究。E-mail：hnyg7906@163.com。

一、研究背景

在今天的智能时代，编程学习已经在各个国家的中小学开展起来，编程能力被视为适应未来社会发展的重要能力之一。在2017年国务院实施的《新一代人工智能发展规划》中明确指出，我国应实施全民智能教育项目，在中小学阶段设置人工智能相关课程，逐步推广编程教育[1]。显然编程教育在国家层面得到了重视。

从现今的编程教育发展趋势来看，图形化编程成了中小学开展编程教育的首选方式，如Scratch创意动画编程、基于掌控板的图形化编程、Python语言的海龟编辑器等。这些图形化编程平台都具有以下几个明显的特征：（1）界面可视化，通过直观操作各种“可视”控件方式来完成程序的设计工作，即随时可以看到编程的阶段性结果;（2）语言积木化，通过封装的形式让字符形态的程序语言转换成具有自然语言形态的积木化语言，降低编程语言学习的认知负荷;（3）操作自然化，图形化编程主要通过拖拽和拼接积木的方式进行程序设计，便于学习者对编程代码的控制与操作。

但是，在相关文献的分析与实际调研过程中，也发现在中小学课堂开展编程学习活动中仍存在一些典型的共性问题，比如，编程课程内容的选取、编程工具的选择、编程教学方式，以及编程学习活动的思维与知识、技能关系[2]等，这都会影响编程学习活动的开展。因此，本研究在实际调研中小学编程学习活动实践的基础上，通过深入分析与思考，拟提出以下问题进行研究：（1）在图形化编程学习中，学习建模是否有必要成为学习中的一个重要环节，哪类建模方式（支架式与开放式）会有助于计算思维的提升;（2）在编程学习过程中，自我效能感是否会影响学生学习活动的开展;（3）在配对式合作编程模式中，不同组别的学习行为存在着哪些差异，这是否影响合作学习活动的开展。

二、关键概念：计算建模与计算思维

（一）计算建模

计算建模就是为了理解编程问题而对实际问题做出的一种抽象理解，形成对编程问题的一种无歧义性的可视化文本描述，是运用系统设计思维，借助计算机语言符号、数学逻辑结构和统一建模语言（UML）等领域工具与方法来建立模型。

面向编程教育的计算建模方法一般分为两类：一是对问题过程的建模方法，二是对问题实体的建模方法。前者是从问题分析的视角强调问题概念化的思维方式，后者是从问题描述的视角着重问题概念化的表现形式。无论哪种建模方式运用在编程活动中，都有各自的优缺点。因此，在编程活动中选择哪一种编程建模方式需要根据问题的主要矛盾，结合两种方法的优点寻求最佳问题解决途径。本研究将从问题的建模方法出发，将建模具体形式分为支架式和开放式。其中支架式建模，是一种在建立模型过程中对关键问题给予一定的额外解释或者指示，为学生在实现解决问题过程中提供思维化线索的认知策略[3]。这种策略能减轻学生的紧张感或焦虑感，但也容易让学生在建模过程中思維受限。开放式建模，是一种没有给学生任何额外解释或者指示，主要让学生在建模过程中能够最大化发挥想象空间，为问题解决寻找最优路径，这种方式解除了学生在建模过程中的思维禁锢，满足了学生自由想象与创新设计的思想，但也容易让学生陷入无从下手或者对问题无法聚焦的困境之中。

（二）计算思维（Computational Thinking，CT）

计算机教育家Pepert在1996年第一次提出了计算思维概念的内涵，认为“计算思维体现了改变学习者学习其他事物的方式”[4]。培养学生的计算思维，需要引导学生像计算机科学家那样在解决问题过程中利用编程方式促进计算思维发展。尽管计算思维有不同的定义，但已有研究表明，计算思维与领域知识库、学习策略、评估、工具、因素和能力建设这六个方面关联密切[5]。因此，计算思维对于当今乃至未来学生发展的必要性已得到广泛认同，在世界范围内被认为是21世纪的基本技能之一。

本研究主要以凯伦·布伦南、米切尔·雷斯尼克在儿童编程研究中对计算思维的评估与界定为基础，即计算思维被视为一种解决问题的方法论，体现了学生在制定问题以及设计解决方案时所涉及的思维过程，以便解决方案能够利用信息技术的方式来执行。这一界定涉及三个可操作维度：计算概念（设计者在编程时使用的概念，如数据、运算符、条件句、并行、事件、循环、序列等）、计算实践（设计者在编程开发中所涉及的思考与学习过程，即建构的过程）和计算观念（设计者在表达、联结和质疑中形成的关于周围世界的自身认知视角）[6]。本研究根据这三个维度设计与开发计算思维水平测量表，便于后续研究的实施。

（三）计算建模与计算思维的内在关联

计算思维与计算建模存在着天然的内在关联，主要表现在以下几个方面：首先，两者都对促进人的思维发展具有一致的逻辑起点，无论是计算建模，还是计算思维都关注着学习者养成科学严谨的思维方式、能力与习惯。其次，培养计算思维是学习者计算建模学习活动中重要的目标之一。学习者在计算建模的描述、结构化、重用、修正、改进等过程中强调了计算思维的运用，如果没有学习者的分析、表征、推理、迭代等深层次思维活动的介入，那么计算建模活动就会停留在浅层性认知上，所以，在建模过程中也实现了对计算思维的培养。最后，计算建模中的关联思维能力是学会计算思维的重要体现。计算思维活动强调了关联思维能力，显然如何获取这种关联关系，就是体现学习者运用计算建模方式去归纳、抽象、挖掘问题中的关联结构，最终实现对问题的解决。因此，获取关联思维能力是学会计算思维的重要体现。44DEDAA2-D71C-458B-92D5-F1A29B988D47

三、促进初中生计算思维发展的教学模型：计算教学法

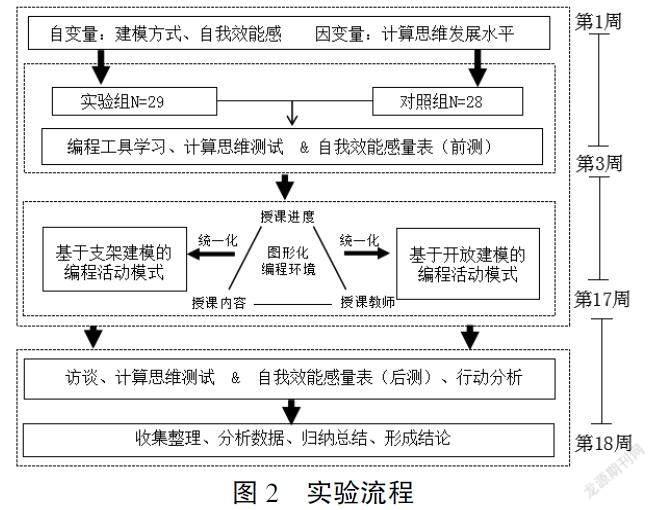
本研究旨在信息技术教学过程中以学生计算思维发展为基本目标，借助计算建模为学习中介设计统一的教学方法，即计算教学法。这一教学法以APOS（A—行动、P—过程、O—对象、S—模式）理论为基础，其原因是APOS理论与计算思维之间有着密切的联系，而且相关研究也表明，借助APOS理论可以使用计算程序的方式来培养学生的心智与创造力[7-8]。同时，结合我国《普通高中信息技术课程标准》（2017年版 2020年修订）[9]和美国国际教育技术协会、计算机科学教师协会（ISTE &CSTA，2011）[10]针对中小学K-12 教育提出的计算思维能力的操作性定义为教学设计依据，提出了以“问题识别与分解—数据抽象与表征—解决问题与评估—学习迁移与反思”为主线的教学过程。具体如图1所示。（1）问题识别与分解阶段，重点让学生形成问题意识。一是能够理解情境中的问题，并能分析问题的关键所在，即需要解决什么样的问题;二是针对已知边界条件能够对问题进行细化，形成问题的基本结构。（2）数据抽象与表征阶段，主要是让学生学会建模，即借助数据抽象思维，通过建立模型来刻画问题。（3）解决问题与评估阶段，表现为学生能够独立形成解决问题的方案，即合理选择算法，以编程方式来解决问题，继而实现问题解决过程的自动化。（4）学习迁移与反思阶段，借助反思与学习迁移，强化学生系统化联结思维，拓展问题域。

四、实证研究

本研究将获取的数据从三个方面进行实证分析。首先，分析实验组与对照组以计算思维测量结果为学习成绩的总体差异性。其次，分析建模方式、自我效能感（自变量）对学习成绩（因变量）的影响。其中建模方式分为开放式与支架式两种不同的类型，自我效能感则分为高自我效能感和低自我效能感两种不同水平。最后，考察在配对式合作编程模式中，不同组别学习行为表现上的差异。另外，本研究选择智能掌控板作为编程工具，该工具是盛思公司开发的一款融学与教于一体的开源硬件，其特点是在不外接设备的情况下也能快速设计多种创意智能作品。

（一）研究对象

研究对象为温州市某中学八年级学生，整体上他们对编程学习有一定的经验，但是基于开源硬件的编程学习还处在初级阶段。另外，在可选择的8个班级中，前测筛选出实验组29人（男生14人，女生15人）、对照组28人（男生12人，女生16人），学生年龄处于12—15岁之间。

（二）研究工具

1. 计算思维水平测量表

本研究以Brennan和Resnick提出的计算思维三维框架为依据[6]，在分析《浙江省义务教育信息技术新教材（八年级上）》中的案例和习题的基础上，结合CTS、CTt、CTPA[11]量表的设计思路与理念开发了计算思维前测和后测的量表，两份测量表题项各20道。測量表采用克隆巴赫α系数（Cronbach α）作为度量方式进行信度分析[12]，结果表明，前测量表Cronbach α=0.830，后测量表Cronbach α=0.756，在整体上两份测量表的信度可以接受。同时，效度检验显示分维度KMO值均>0.7，Bartlett球体检验为0.007，整体效度良好。

2. 自我效能感问卷

本研究的自我效能感问卷是在黄国祯教授团队开发的量表[13]基础上进行优化与改编。量表采用李克特5点评分法，其Cronbach系数为0.89，说明该量表具有突出的内部一致性。量表选项由“非常同意”“较同意”“没有什么意见”“不同意”“非常不同意”组成，各选项得分依次降低，共计6题，总计30分。学生成绩越高，意味着自我效能感水平也越高。

3. 滞后学习行为分析测量表

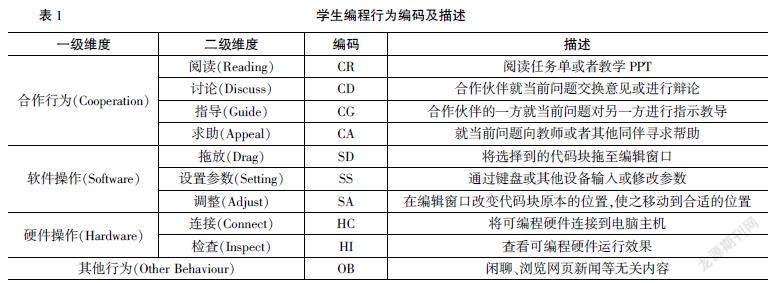
研究通过分析课堂录像视频中学生的编程行为，筛选出无关的偶发性编程行为，结合相关研究文献[14]，设计了阅读、讨论、指导、求助、拖放、设置参数、调整、连接、检查和其他行为等10种编程行为类型，并将其归纳为合作行为、软件操作、硬件操作和其他行为四个维度，作为行为序列分析的指标。表1呈现的是10种编程行为的一级维度名称、二级维度名称、研究编码以及行为描述。

（三）实验流程

本实验流程如图2所示。首先通过前测筛选出实验组与对照组人数。在学情分析后，由于学生是第一次接触mPython软件和掌控板硬件，前三周让学生熟悉编程工具，三周后对学生计算思维水平进行前测，并填写自我效能感量表。在接下的14周编程学习活动中，由同一位教师统一授课，其中实验组采用支架建模的方式开展编程活动，对照组采用开放建模的方式。学习活动结束后，对学生计算思维水平和自我效能感进行测试，同时随机抽取实验组学生进行学习活动满意度的访谈，以了解学生在编程学习活动中的感受与体验。

（四）数据分析

1. 研究一：纵横对比分析实验组与对照组在以计算思维测量结果为综合成绩以及不同维度上均值之间是否存在着显著性差异

首先，在横向对比分析中采用独立样本T检验方法对两组学生的计算思维进行前后测分析。分析表明，实验组和对照组学生在前测计算思维（p=0.568>0.05）测量综合成绩上没有显著差异，这说明两个组在计算思维能力水平上基本一致，可视为同质组并选择为实验对象。但是，两个组后测计算思维水平结果上却存在显著差异（p=0.000<0.01），同时计算概念维度（p=0.030<0.05）、计算实践维度（p=0.003<0.01）、计算观念维度（p=0.015<0.05）也存在着差异，其中计算实践差异性最为显著。另外，实验组均值成绩都明显优于对照组。

其次，纵向对比分析主要对两个组成绩是否各自会有不同程度的提升进行了配对样本T检验分析。结果表明，实验组计算思维测量成绩（p=0.000<0.01）在前后测上存在显著差异，而且计算概念、计算观念维度上也呈现显著性差异，但是计算实践（p=0.080>0.05）维度没有呈现显著性差异。对照组前后计算思维测量成绩与计算概念维度都不存在显著差异，但是，计算实践、计算观念维度上前后测存在显著性差异。两个组前后测在成绩均值上大部分有所提高，但发现对照组的计算实践均值成绩反而有所降低（M前=25.71>M后=17.28），结果有点出乎意料，需要进一步分析与思考。44DEDAA2-D71C-458B-92D5-F1A29B988D47

2. 研究二：分析建模方式与自我效能感对计算思维测量成绩是否产生交互效应影响，以及进一步分析三者之间的内在关系

这一部分采用双因素析因方差分析法对数据进行处理[21]，其结果见表2。结果表明：以建模方式和自我效能感为自变量，对学生的计算思维（F=0.63，p=0.433>0.05）测量成绩没有显著交互影响，与计算概念、计算实践、计算观念等分维度也不存在显著统计交互性。在此基础上，对建模方式以及自我效能感这两大自变量各自进行单因素方差分析。分析表明：不同建模方式对计算思维测量成绩（F=16.05，p=0.000<0.01）影响有显著差异，并且在计算概念、计算实践和计算观念三个分维度上也有显著性差异;而不同自我效能感对计算思维测量成绩（F=1.60，p=0.211>0.05）影响没有显著差异，而且在计算概念、计算实践和计算观念上也都没有显著性差异。

3. 研究三：分析在配对式合作编程模式中，不同类型的学习小组会引起什么样的学习行为，其行为序列的差异有哪些，其原因是什么

这一部分采用滞后序列分析法（Lag Sequential Analysis，LSA）进行分析，其目的是从配对式合作编程学习过程中的质性数据来解读学生的学习行为，并对比不同性别在主导配对式合作编程学习过程中是否使学习行为模式出现显著性差异。

当确定编码方案后，从实验组的14个小组中随机抽取4个典型小组的视频进行分析，包括男生—男生组（BB组，由男生主导的男生小组）、男生—女生组（BG组，由男生主导的男女生混合小组），女生—男生组（GB组，由女生主导的男女生混合小组），女生—女生组（GG组，由女生主导的女生小组）。另外，对两位编码者行为一致性进行检验，本检验的克隆巴赫系数为Alpha=0.891，说明两位编码者的编码行为具有一致性[15]。通过对20多分钟的学习活动视频的分析，两位编码研究者共得到583个学习行为，并形成了学习行为的原始序列和行为转换频率的统计。

其中，BG组在“合作行为”（74.3%）、“软件操作”（73.6%）、“硬件操作”（74.0%）三个一级编码类别中行为频次都是最高。另外，在“合作行为”二级编码类别中，GG（1.8%）和BB（1.8%）组在“求助”频次、GB组（7.7%）和GG组（0%）在“指导”频次数量上都很低;从“合作行为”的行为频次的统计数量上来看，女生主导的合作学习行为数量（16.4%）相对较低;在“软件操作”学习行为频次分析上，“设置参数”（26.8%）与“调整”（35.4%）的学习行为数量相对较低。值得注意的是，虽然学习行为出现的频次并不能成为衡量学生学习效果的唯一指标。但是，我们从学习频次分析上能够看到哪一类小组在学习活动中能引起什么样的学习行为。

为了进一步探究不同性别组合的合作小组在学习行为序列上的差异，本研究借助GSEQ软件开展滞后序列分析。将BB、BG、GB、GG小组的一系列编码后得到的行为序列按时间出现的先后顺序输入软件工具之中，并生成调整后的残差表。最后，根據调整后的残差表，将Z-score>1.96的行为绘制成行为序列转换图[16]。这四个小组的学习行为的序列图如图3～图6所示，每两种学习行为之间连线上的数值标示了Z值，连线越粗则表示两种行为先后出现的概率越大。

（1）男生—男生（BB）组在遇到问题时易向外求助，同时也具有良好的编程行为习惯。

BB小组一共产生了10种行为序列，Z值都大于1.96，达到显著水平。具体如图3所示。从图中发现， BB组的学习行为模式具有以下特征：①“指导行为”与下一个行为之间的Z值都没有达到显著性水平，在BG组和GG组都出现类似的现象。为什么该小组在配对式合作学习中难以出现“指导行为”？经访谈后发现，其背后的原因是他们在内心里更倾向接受讨论方式，而不是指导;讨论方式能使他们站在平等身份的视角进行交流。②在“检查→求助”行为序列达到了显著水平，同时在“求助→指导”也达到了显著水平，这说明BB组在运行硬件设备的检查过程中，在遇到问题时并没有进行相互深入讨论，而是借助外组同伴的帮助解决问题。③“调整→设置参数”行为序列达到了显著水平，这表现出了学生在调整图形化编程模块后及时设置相关参数的良好习惯，这种习惯减少了编程错误的出现。但是该行为序列并非唯一的走向，还存在“调整→其他行为”的支路，这也表明学生在完成部分模块的调整后，还会有闲聊或者浏览新闻网页的行为出现。

（2）男生—女生（BG）组编程合作行为较为丰富，同时循序渐进操作软件，在遇到问题时能够深入讨论。

在BG小组中一共产生了13种显著行为序列。具体如图4所示。从图中可以发现，该组的学习行为模式具有以下特征：①由男生主导的混合配对小组更能够激发“异性效应”，让合作学习发挥出最佳效率。同时，无论在行为数量还是在行为类型上，BG组都成为了四个小组中最优的配对合作方式。②在图中序列行为模式上，“拖放→调整”“调整→设置参数”“设置参数→阅读”“阅读→拖放”这4个行为序列形成了一个闭合循环，这说明BG组在编程过程中会循序渐进地对图形化编程模块进行操作，并借助导学单进行模块调整与思考，这种行为序列模式反映了该小组有着良好的自主学习行为。③“讨论→检查”行为序列达到了显著水平，这说明BG组在运行硬件设备的检查过程中，就编程问题进行了深入讨论并及时调试设备。但是该行为序列还存在“讨论→其他行为”以及“检查→其他行为”的分支，这也表明了与其他小组一样出现了“其他行为”。

（3）女生—男生（GB）组在合作学习过程中，倾向于先组内讨论，制定问题解决计划，然后再开始编程，另外，相较于男生—女生组，显著性的行为序列相对较少。

在GB小组中一共产生了9种显著的行为序列。具体如图5所示。从图中可以发现，该组的学习行为模式具有以下特征：①“讨论”行为是所有行为序列的起点。通过课堂观察和课后访谈得知，学生在合作学习过程中，倾向于组内成员先相互探讨问题解决的方案、制定计划和分工等，然后开展学习活动。但GB组学生“讨论”行为后出现了“其他行为”。②GB组和BG组在学习行为序列上存在着较大差异。首先，BG组行为序列对显著性要高于GB组。在BG组中有8对Z值大于3的行为序列对，而GB组没有;其次，BG组的行为序列对组合数量多于GB组。经过课堂观察以及现场访谈发现，相较于BG小组，GB小组深入交流较少，而且在编程过程中出现问题时男生没有出现积极学习行为，而且给予同伴的建议也相对较少，这也导致了GB组与BG组在行为序列上产生了差距。③GB组只有在“检查→阅读”行为序列上达到了显著水平。这说明GB组在“检查”程序运行结果的同时，倾向“阅读”相关资料寻找程序运行效果不佳的原因以及解决方式。但“阅读”之后并没有出现及时“调整”编程模块等操作行为序列，这说明该组自主解决问题的能力还有待提升。44DEDAA2-D71C-458B-92D5-F1A29B988D47

（4）女生—女生（GG）组在合作学习中遇到问题偏向于小组内部讨论解决，同时也易出现注意力转移与学习无关行为的现象。

在GG小组中5种行为序列达到显著水平，其行为序列图如图 6 所示。从图中可以发现，该组的学习行为模式中具有以下特征：①与BG组、GB组和BB组相比，GG组的行为序列类型较为单一，而且行为关联频次不高。对访谈记录与视频分析后，GG组对该学习任务没有产生积极的学习兴趣，认为这次学习任务太难，讨论后也没有解决问题，对任务完成与否抱着消极的态度。最终，该组也不会有积极的学习行为出现。②“其他行为→检查”“检查→其他行为”行为序列虽然达到了显著水平，但是，与其他组别还是存在一定的差异，因为GG组中的“其他行为”与“检查”形成一种双向关联关系，这说明该组在检查学习行为上，会频繁出现闲聊或浏览网页新闻、娱乐等行为。

五、问题讨论

在上述研究过程中，我们发现还有一些共性的问题值得进一步探讨。首先是自我效能感的问题。无论实验组还是对照组，自我效能感都没有发挥出应有的正面效应，拥有不同水平自我效能感的学生在总体成绩上没有显著性差异，高自我效能感与低自我效能感之间的均值成绩也差异不大。具体如图7所示。

自我效能感体现了个体对自己是否有能力完成某一项任务所进行的推测与预判，也是个体自信心的表现[17]。为了深入了解这一现象背后的原因，本研究对部分学生进行了访谈，有些学生认为，“相比语数外等课程，信息技术课的要求并不高，即使有些程序完成了，也没有什么成就感。”另外，一些学生则反映，“基于开源硬件的编程学习还是有点难度，第一次接触嘛，学习上的困难比较多也影响了学习的信心。”经访谈，究其原因有三个方面：一是信息技术课程地位的问题;二是初学基于开源硬件的编程，给学生带来了压力;三是周课时的问题，每周一次的课时难以使学习有连贯性，容易让学生失去兴趣。这些问题的解决虽然有制度层面上的阻力，但是教师做好课程单元内容的设计，使学习项目具有连续性，也是一项可行的策略。其次是“其他行为”普遍出现在各个小组的学习过程之中的问题。“其他行为”的频繁出现，说明了在学习过程中有“开小差”现象，如上网看娱乐新闻、闲聊等行为，学习注意力易发生转移;同时也反映出教师在课堂教学中的监管与指导力度上存在问题。一旦课堂缺乏有效的监管与指导，很容易导致小组在寻求教师帮助时，学生会由于等待时间过长和教师监管不到位导致出现这一现象。为了防止这些“其他行为”的频繁出现，需要教师一方面合理安排好学生用网时间，从技术上控制好无关行为的出现;另一方面，教师在小组合作组织上可以采用能力分组与意愿分组方式，让小组内有制约机制;同时安排好个人学习任务单，明确学习任务与目标。

六、总结与建议

本研究在图形化编程环境中，以建模方式作为研究变量，并探讨了不同建模方式、自我效能感对计算思维测量结果的影响进行了研究。研究发现，编程建模方式不仅影响了学习成绩的提升，而且也成为学生学习编程的一种思维方式。尤其是支架式编程建模方式，给学生提供了思考问题的线索，以线索为基础分析问题所关联的基本要素，厘清问题结构并寻找合理的解决方案。由于多方面的影响，自我效能感没有发挥应有的功能，未能显著性影响学习成绩。为了进一步探讨学习行为，本研究借助滞后序列分析法对不同性别主导配对式合作编程学习行为进行分析，其结果是不同小组的学习行为序列模式出现了显著性差异，同时在这些差异中也发现了一些共性问题。针对这些问题，本研究提出以下几点建议，以便今后更加顺利地开展此类学习活动。

（一）在图形化编程环境中需要重视编程建模这一方法，让建模成为学生计算思维发展的重要支架工具与途径

在编程学习活动中，通过建立模型的方法，一方面能够澄清相关问题假设，帮助学生更有逻辑地思考并理解问题的核心所在，帮助学生对问题建构起某种内部表征（概念模型）;另一方面表征的模型为小组成员提供了一个可供讨论的对象，其表征过程所包含的事实、想法或假说、学习重点以及行动计划也成了他们在解决问题过程中增加理解和交流思想的基础。显然，建模方法为学生认知发展提供了支持，包括检验假设、猜想、推理以及许多重要的认知技能[18]。因此，在中小学编程教育中建模方法成了培养学生计算思维不可或缺的认知工具。显然，建模不仅仅只是一种表征客体事物（问题）原型的映射过程，更是学生发展计算思维方式的一种认知途径。当学生在编程活动中为了解决某一实际问题，通过建模方式构建了问题模型，而这一模型信息会在大脑中被加工编码并内化为自身知识体系，最终被学生所“理解”。显然，这就成了培养计算思维的一种重要学习方式：基于模型的学习。

（二）编程学习活动的开展不仅需要关注编程学习内容的实用化设计，而且还需要考虑活动组织的精细化安排

在编程学习中，学习内容设计成为了教学活动开展的“主旋律”。如何让学生能够成功依赖于自己的认知策略、先前知識和动机，并有责任地组织学习活动，这是学习内容设计的重中之重。显然，在学习内容设计上，首先应站在学习者的角度来进行总体构思，在了解基本学情的基础上合理搭建活动要素（如学习组织方式、知识传递策略、评估学习方式等）;其次，学习内容应尽量融入学生的生活经历，让所学的编程知识与技能能够迁移并应用于生活实践之中，超越自身已有的经验，避免学习认知的单调性变化;最后，学习内容在组织策略上需要多样化，如多通道策略、多表征策略、支架策略等综合运用，凸显在学习活动上的多变性，旨在发挥学生的主动性，让学生获得更多的自我效能感。另外，在活动组织上需要精细化，不仅从个人意愿与兴趣基础上进行分组，还应考虑能力分组方式，促进不同小组成员之间相互依赖与相互监督;同时重视学习活动过程中的监管问题，防止课堂出现过多的“无关行为”。

[参考文献]

[1] 新华社.国务院印发《新一代人工智能发展规划》[EB/OL].（2017-07-20）[2019-07-24].http：//www.gov.cn/xinwen/2017-07/20/content 5212064.htm.44DEDAA2-D71C-458B-92D5-F1A29B988D47

[2] TIKVA C， TAMBOURIS E. Mapping computational thinking through programming in K-12 education： a conceptual model based on a systematic literature review[J]. Computers & education， Volume 162， 2021， 104083， https：//doi.org/10.1016/j.compedu.2020.104083.

[3] VAN DE POL J， VOLMAN M， BEISHUIZEN J. Scaffolding in teacher-student interaction： a decade of research[J]. Educational psychology review， 2010， 22（3）：271-296.

[4]  西摩.佩珀特.因计算机而强大——计算机如何改变我们的思考与学习[M].梁栋，译.北京：新星出版社，2019.

[5]  TIKVA C， TAMBOURIS E. Mapping computational thinking through programming in K-12 education： a conceptual model based on a systematic literature review[J]. Computers & education， 2021（162）：104083.

[6] BRENNAN K， RESNICK M. New frameworks for studying and assessing the development of computational thinking[C]// Proceedings of the 2012 Annual Meeting of the American Educational Research Association， Vancouver， Canada. 2012， 1： 25.

[7] VIDAKOVIC D， DUBINSKY E， WELLER K. APOS theory： use of computer programs to foster mental constructions and student's creativity[M]// Creativity and technology in mathematics education. Cham， Switzerland： Springer， 2018： 441-477.

[8] CETIN I， DUBINSKY E. Reflective abstraction in computational thinking[J]. The journal of mathematical behavior， 2017， 47： 70-80.

[9] 中华人民共和国教育部.普通高中信息技术课程标准（2017 年版 2020 年修订）[M].北京：人民教育出版社，2020.

[10] ISTE & CSTA. Operational definition of computational thinking for K-12 education[EB/OL].（2014-04-15）[2021-08-15].https：//iste.org/explore/computational-thinking/computational-thinking-all.

[11] XIAODAN Tang， YUE Yin， QIAO Lin， et al. Assessing computational thinking： a systematic review of empirical studies[J]. Computers & education， Volume 148， 2020， 103798， https：//doi.org/10.1016/j.compedu.2019.103798.

[12] TAVAKOL M， DENNICK R. Making sense of Cronbach's alpha[J]. International journal of medical education， 2011（2）： 53-55.

[13] HSIA L H， HUANG I， HWANG G J. A web-based peer-assessment approach to improving junior high school students' performance， self-efficacy and motivation in performing arts courses[J]. British journal of educational technology， 2016， 47（4）：618-632.

[14] LYE S Y， KOH J H L. Case studies of elementary children's engagement in computational thinking through scratch programming[M]// Computational thinking in the STEM disciplines. Cham， Switzerland： Springer， 2018： 227-251.

[15] 藍石.基于变量类型做好统计分析[M].重庆：重庆大学出版社，2014.

[16] BAKEMAN R， GOTTMAN J M. Observing interaction： an introduction to sequential analysis（2nd ed.）[J]. Technometrics， 1997， 34（1）：112-113.

[17]  A·班杜拉.自我效能：控制的实施[M].缪小春，李凌，井世洁，张小林，译.上海：华东师范大学出版社，2003：12.

[18]  D·H·乔纳森.技术支持的思维建模（第三版）[M].顾小清，译，上海：华东师范大学出版社，2008：13.44DEDAA2-D71C-458B-92D5-F1A29B988D47