基于机器学习的内涝积水深度预报方法研究
2022-04-27张响亮许文华杨明灿王万宣梁宝元
张响亮 许文华 杨明灿 王万宣 梁宝元
(1.仙游县气象局,福建 莆田 351200; 2.莆田市气象局,福建 莆田 351100)
准确预测内涝点积水深度有利于防洪力量的合理调配,提高防汛救灾部门的工作效率,降低内涝造成的人员伤亡和经济损失[1]。随着全球气候变化,强降水及其不同尺度极端事件频发[2],城市内涝出现的频率及危害将不断增大[3],面对严峻的防洪防涝挑战,内涝点积水深度预测模型研究成为国内外热点。城市水文模型经历了集总式水文模型向更具物理意义的分布式水文模型发展[4],国内外常用的内涝模型有美国环境保护署的SWMM模型(暴雨洪水管理模型)、法国电力的TELEMAC-MASCARET(水动力学和水文学领域的高性能数值仿真开源软件)等。国内学者在SWMM模型的基础上开发出了许多适用于我国的内涝模型。随着人工智能技术的发展,应用机器学习方法建立的回归模型因其预测效果较水文模型并不逊色,又具有计算快捷的优势,具有较好的实用性[5]。研究表明,降水是内涝灾害最主要的诱发因素[6]。此外城市内涝还受到地表汇流、管网排水和河道排涝等水文动力过程影响[7]。
综上所述,水文模型受到地形数据、降水数据、运算能力的影响,存在较大局限性。本文基于内涝点积水深度资料和临近气象观测站小时降水量资料,设计滞后系数与堵塞系数的计算方法,滞后系数可表示地表汇流对积水深度的影响,堵塞系数可表示排水设施的运行情况。将滞后系数、堵塞系数、小时雨量和前一时次积水深度作为输入层,采用机器学习中的岭回归方法建立了内涝点积水深度预报方程。预测检验显示了其较好的实用性。
1 资料与方法
1.1 资料选取
雨量数据选用莆田市国家气象观测站(以下简称莆田站)的逐小时降水数据,积水深度数据为莆田市荔园路才子路口(以下简称才子路口)的积水深度数据,莆田站与才子路口直线距离约3km。
选用2018年6月6日至8月31日莆田站逐小时降水量和才子路口整点积水深度建立回归方程。回归方程检验资料选用2018年9月1日至2018年9月30日莆田站逐小时降水量和才子路口整点积水深度。
1.2 研究方法
1.2.1 回归方程
通过特征值与目标值进行拟合,可建立回归模型从而实现利用特征值对目标值进行预测。机器学习在进行回归模型预测时,预测值和实际值之间存在一定误差。找到最优的估计参数使误差最小,即可建立最优的回归模型,但在数据量较少或者数据有共线性时,会导致权重趋于无穷大,需要引入一个惩罚项来改善这一问题[5]。
1.2.2 岭回归方程
岭回归算法是基于最小二乘法的有偏估计回归方法,加上了L2正则化表达式,考虑了各特征值的重要程度,能够适应共线性问题。虽然该方法损失了无偏性,但是能够对含共线性数据有较好的拟合效果。本文采用岭回归算法建立内涝点积水深度预报方程。
1.2.3 积水深度预报方程建立
基于2018年6月6日至8月31日莆田站逐小时降水数据和才子路口积水深度数据,计算滞后系数与堵塞系数。将滞后系数、堵塞系数、当前小时雨量和前一时次积水深度作为输入层,采用岭回归方法,得到才子路口积水深度预报方程。
2 数据优化
滞后系数与堵塞系数的计算需要连续性的雨量数据和积水深度数据,部分数据存在以下明显错误:①降水过程停止后,低处的积水无法正常排出,导致内涝点积水深度始终维持在较低的数值;②在小尺度的降水过程中,无法准确获取内涝点的降水情况,导致降水与积水深度变化不一致。为此,在建立回归方程前,需要对内涝点积水深度数据进行修订。
2.1 低值积水数据处理
积水深度下降至低洼处时,积水无法汇入排水设施,排水速度异常缓慢。使用该数据建立的回归方程整体排水速度偏慢,导致预测的积水深度偏高。因此需要判断低洼处积水深度的临界值,当积水深度低于临界值时,计算出正常排水速度下的积水深度。
2.1.1 积水深度临界值计算
原始数据中的积水深度下降至临界值后,积水深度下降缓慢,导致积水深度低于临界值的数据量较大。故认为积水深度低于某一值的数据量超过设定的阈值时,该深度为临界值。本文设置的阈值为95%,计算的积水深度临界值为2cm。
2.1.2 正常排水速度计算
积水深度大于临界值时,积水可以顺利汇入排水设施。筛选出积水深度大于临界值、临近2个时次无降水、积水深度比上一时次低的数据,计算积水深度降低的平均速度,作为正常排水速度,本文计算的正常排水速度为1.03cm/h。
2.2 积水深度异常上升
原始数据中,部分数据出现“降水停止后的积水深度依旧上升”的情况。使用该数据建立的回归方程,降雨量的权重明显偏低,甚至导致降雨量与积水深度呈反比。故使用正常排水速度计算出的积水深度替换临近两个时次无降水、且积水深度大于前一时次积水深度的数据。
3 特征值选取
内涝点的积水深度主要受降水、前期累计降水、地表汇流、管网排水等因素影响。本文选用小时雨量、前一时次积水深度、滞后系数与堵塞系数作为影响积水深度的预报因子。以下介绍滞后系数和堵塞系数的计算方法。
3.1 滞后系数
姜晓岑等[8]指出,积水一般滞后降水约5~30min出现。由于小时雨量数据无法准确描述降水的时间分布情况,若较强的降水集中出现在中后时段,当前时次的积水深度没有明显变化,而是影响下一时次的积水深度。因此降水导致的积水深度若没有达到预期的积水深度,则认为部分降雨量将滞后影响下一时次的积水深度。实际深度与预期深度相差越大,滞后系数也越大。积水深度预期值与滞后系数计算方法如下。
3.1.1 积水深度预期值
积水深度预期值计算公式如下:
hi=hi-1+(Δh×ri-v)
式中,hi为当前时次积水深度预期值,hi-1为前1小时的积水深度,Δh为单位雨量产生的积水深度,ri为当前时次降水量,v为正常排水速度。
计算单位降水量产生的积水深度,需要筛选降水超过排水设施承受临界值的数据。由于降雨量超过临界值的比重较大,在产生积水的数据中,分别计算降雨量大于50mm、40mm、30mm、20mm、10mm时产生积水的数据比重,当比重超过设置的阈值时,认为对应的雨量为产生积水的雨量临界值,本文阈值设置为95%,计算出的临界值为10mm。由于产生积水的过程中,排水设施使积水深度下降,因此雨量产生的积水为积水深度实际变化值与排水速度之和,单位雨量对积水深度增长值的计算公式如下:
式中,Δh为单位雨量对积水深度增长值,hi为当前时次积水深度,hi-1为上一时次积水深度,v为积水下降速度(积水下降时为正值),ri为当前时次降雨量,m为筛选后的样本总数,本文计算的单位雨量对积水深度增长值为0.04cm/mm。
3.1.2 滞后系数计算
将上一时次积水深度的预期值与积水深度实际值的差值,作为当前时次的滞后系数,若滞后系数大于0,则考虑滞后降水影响当前时次的积水深度,若滞后系数小于0,则不考虑滞后降水对积水深度的影响,滞后系数修订为0。
3.2 堵塞系数
排水设施在使用过程中存在被杂物堵塞等情况,导致排水速度降低。考虑堵塞系数,可以解释某些雨量较为均匀的降水过程中,积水深度变化不规律的情况,该系数亦可用于判断各内涝点排水设施是否存在堵塞。堵塞系数计算公式如下:
bi=(hi-1-hi-2)-(ri-1×Δh-v)
式中,bi为当前时次堵塞系数,hi-1、hi-2为前1小时和前2小时的积水深度,ri-1为当前时次的降雨量,Δh为单位雨量对积水深度的贡献,v为积水深度下降速度。
计算得到的堵塞系数越大,则说明堵塞情况严重。例如降水停止后,计算的(ri-1×Δh-v)为负的定值,但若堵塞情况严重时,(hi-1-hi-2)应为趋近于0的负值,计算的b值大。若堵塞情况较轻,则(hi-1-hi-2)项数值越小,计算的b值越小。
4 模型训练及检验
4.1 算法与参数选取
scikit-learn库(针对Python 编程语言的机器学习库)中含有多种机器学习算法[9],本文选择scikit-learn库中岭回归算法对内涝方程进行训练[10]。岭回归算法是基于最小二乘法的有偏估计回归方法,加上了L2正则化表达式,考虑了各特征值的重要程度,能够适应共线性的问题。模型输入变量为2018年6月至8月莆田站的小时雨量数据、才子路口的积水深度数据以及计算的滞后系数和堵塞系数。参数solver选择“auto”(可以根据样本量自动选择回归方程的优化方案)、normalize选择“False”(经检验,关闭样本特征归一化后计算的均方跟误差更小),训练出预报方程为:
yi=0.003ri+0.96hi-1+0.286li+0.264bi-0.208
式中,yi为预测的积水深度,ri当前降水量,hi-1为前一时次积水深度,li为滞后系数,bi为堵塞系数。
4.2 模型检验
通过9月1日00时至9月30日23时的积水深度数据对预报方程进行检验,预报结果与实际值的均方误差为0.27cm,说明预报效果较好,但由于9月强降水的出现次数较少,积水深度为0的数据比例较高,因此检验结果无法代表强降水出现时积水深度的预报效果。故筛选9月出现降水过程的数据再次进行检验(9月降水数据中,仅 9月7日14时至9日07时、9月23日08时至24日18时出现较强降水),降水过程的预报结果与实际值的均方误差为1.09cm,总体的预报偏差在2cm以内,能一定程度反映强降水过程的积水情况,但测试数据中出现雨量很小但积水深度突增的情况,可能是由于雨量站与积水点位置偏差导致雨量数据无法反映内涝点的降水情况,因此对于无降水时积水深度上涨的时次无法准确预测。降水过程检验的部分结果见表1。
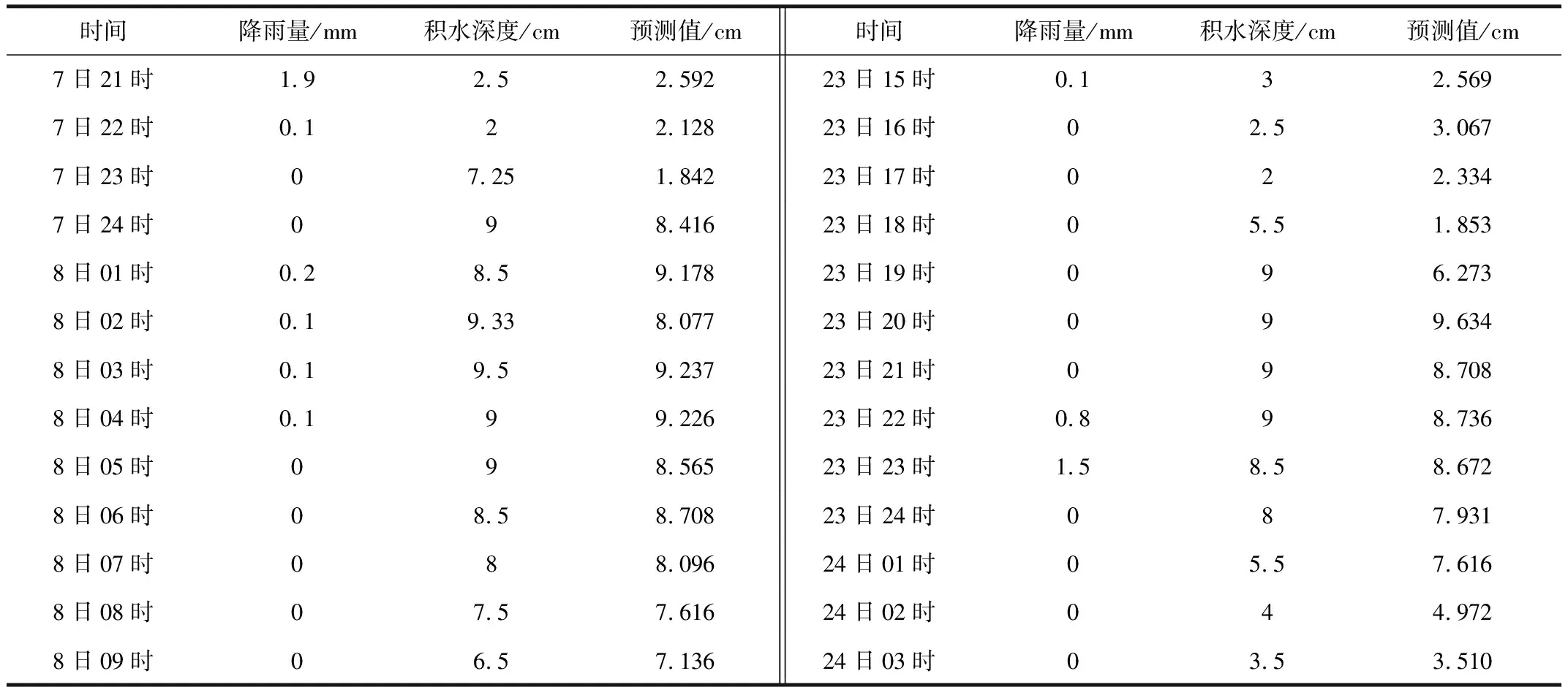
表1 9月降水过程降雨量、积水深度实际值与积水深度预测值
5 结论与讨论
本文利用2018年6月至8月莆田站逐时降水资料、才子路口整点积水深度资料,应用机器学习中的岭回归方法建立了内涝点积水深度预报方程,并使用2018年9月1日00时至30日23时的降水过程进行检验,回归方程的均方误差为0.27cm,降水过程检验结果的均方误差为1.09cm,预报效果较好。
回归方程的效果依赖于实况数据的准确性,若使用更好的初始数据,并且加强内涝点积水深度观测站设备的维护和保障,建立的积水深度预报方程质量更高。此外,本文的滞后系数和堵塞系数在其数值大小上能反映滞后和堵塞的情况,但其系数的具体算法还有待研究。
