高中数学教科书中数学史内容的比较研究——以人教A版(2019版)和北师大版(2019版)为例

刘金海, 代 钦

(内蒙古师范大学 科学技术史研究院， 内蒙古 呼和浩特 010022)

0 引言

2018年初，教育部颁布了《普通高中数学课程标准(2017年版)》[1](以下简称《新课标》)引领新一轮的高中数学课程改革.《新课标》明确指出将数学文化融入高中数学课程内容并对其做出说明:“数学文化是指数学的思想、精神、语言、方法、观点以及他们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献与意义，以及与数学相关的人文活动.”除此之外，给出教科书编写的相关建议：将数学文化融入学习内容中，开拓学生数学视野，激发学生学习兴趣和好奇心，培养学生科学精神，要求教科书编写人员参照在“课程内容”中相应数学文化提示.数学史作为数学文化不可或缺的元素，被关注的热度持续升温，从近几年高考试题数学文化的探析中可见一斑，大量以中外数学史为素材的试题出现在学生的视野中[2].教科书居于教学目标与教学评价的核心环节，是教师教学与学生学习的重要载体，研究对比不同版本教科书中对数学史料的选取与融入方式具有重要的学习价值.

早在1972年第二届国际数学教育大会(ICME-2)就成立了数学史与数学教学关系国际研究小组(international study group on the relations between history and pedagogy of mathematics，简称HPM)专门研究数学史与数学教育.我国于2005年在西安举办了第一届数学史与数学教育研讨会，其后每两年举办一次学术会议对这一领域进行深入研究.伴随着近些年在其理论和实践上的共同发展，数学史融入数学教育方面取得了长足的进步.目前，我国实行“一标多本”的教育政策，即在课程标准的指导下，教科书呈现百花齐放的局面，各个版本也颇具特色.徐文彬等[3]就曾在义务教育课标颁布后，对不同版本的初中教科书中数学史进行了分析，从观念、方法和结果三个方面提出自己的思考.

本研究选取人教A版(包含必修一、必修二、选择性必修一、选择性必修二和选择性必修三)与北师大版(包含必修一、必修二、选择性必修一和选择性必修二)两套高中数学教科书，对其中的数学史主题进行统计分析，比较数学史料在两套教科书中的融入形式，这些内容既反映了教材编写者对新课标的理解与把握，又直接影响着教师与学生的教与学.

1 数学史料量与类的统计分析

1.1 数学史料的主题分布

数学史在新版教科书中的融入体现了高中数学课程改革的要求，凝练着教科书编写者贯彻数学课程标准理念的智慧，承载着数学教学中数学文化教与学的重任.为更好地呈现出数学史料的选取和在具体章节中的安排，对数学史料的主题分布做进一步的统计.概括数学史料主题时使用教科书中的标题或对其进行总结给出，并在各个主题后给出具体页码以供查阅参考.具体内容如表1所示.

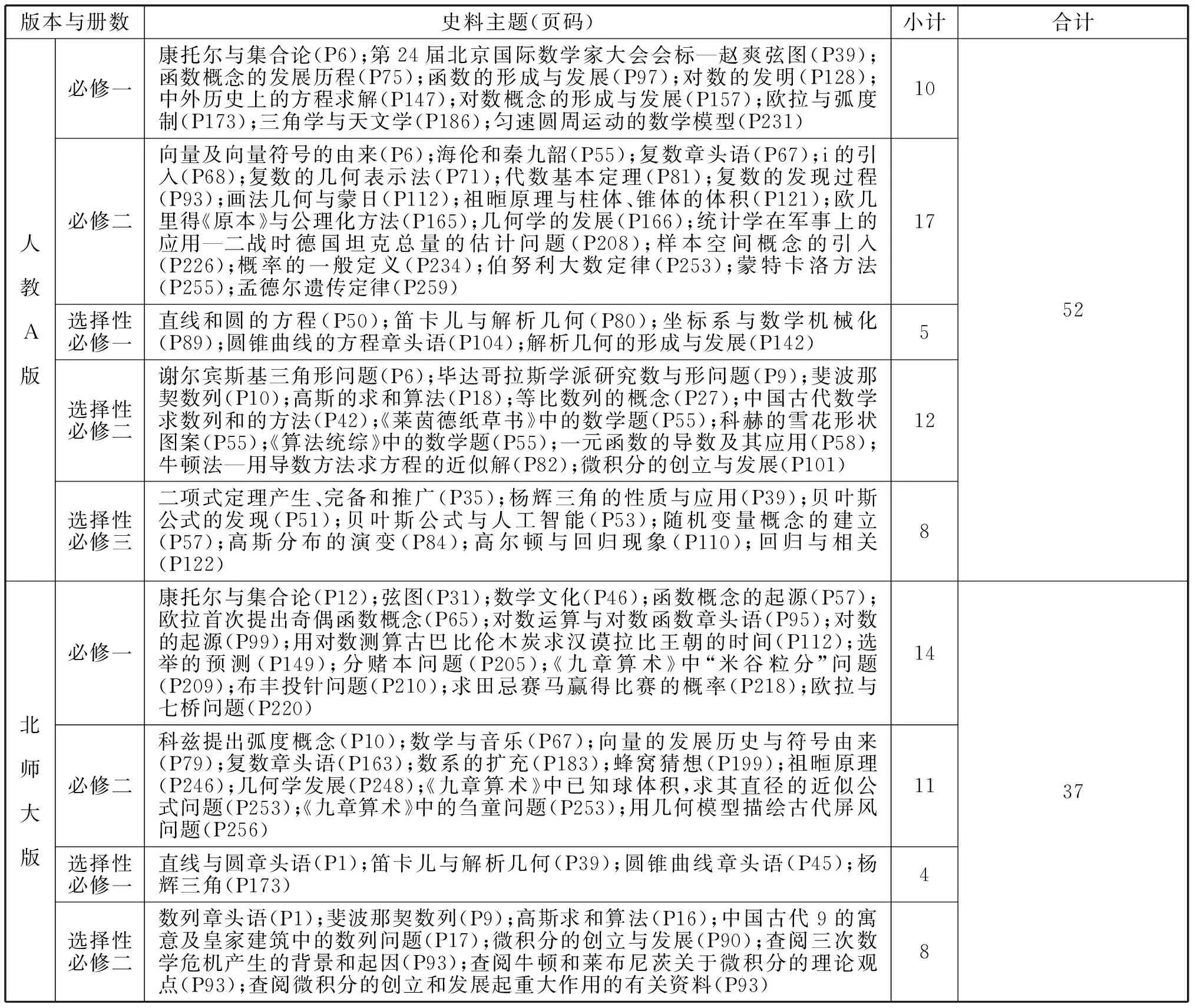
表1 人教A版和北师大版高中数学教科书中数学史料的主题分布

宏观上统计，人教A版数学教科书的五个分册出现数学史料共计52处，北师大版数学教科书的四个分册共计37处，前者在总量上偏多.进一步可发现，两套教科书在选取数学史料和命名主题时有各自的特点，但对一些重要的中外数学史均有保留.例如，《几何原本》《九章算术》等经典数学著作；祖暅原理、杨辉三角和斐波那契数列等脍炙人口的数学故事等.一方面，中小学所涉及的数学大多是16世纪末之前的古典数学，主要以算术、代数、几何(平面几何、立体几何)和三角为主[4]；另一方面，中学数学课程改革经过20世纪的克莱因-贝利运动，在内容设置上以函数内容为主线、充分利用坐标系和尽早讲授微积分等观点在全世界范围内深入人心，这些知识点进而以数学史料做补充，如函数概念的形成、笛卡儿和坐标系及微积分的形成过程等都增加了不同版本教科书中数学史料选取的共性.

微观上分析，除去两个版本的共同点，如在章头语、正文和练习题中的数学史料融入，有以下各自的特征：人教A版数学教科书中有大量的数学史料体现于阅读与思考版块和文献阅读与数学写作部分，并且后者为选学内容在考试中不做要求，增大了学生的自主选择权.北师大版主要呈现在阅读材料中，另外较之于人教A版，北师大版在每一章节前的章头语下附上与该章节主题相符的数学家名言.例如，在必修一第四章学习对数运算与对数函数时，有伽利略的名言：“给我空间、时间和对数，我可以创造出一个宇宙”.寥寥数语就能激发学生求取新知的兴趣.经统计，北师大版教科书中共计出现此类名言16条，其中包含的国内外数学家有华罗庚、陈省身、拉普拉斯、F·克莱因和爱因斯坦等人.

1.2 数学史料的分类统计

依据《新课标》对数学知识内容的划分，必修课程和选择性必修课程中均包含“函数”“几何与代数”“概率与统计”“数学建模活动与数学探究活动”四条主线.另外在必修课程中加入了预备知识，帮助学生在高中数学课程中做好学习心理、学习方式和知识技能等方面的准备，完成初高中学习的衔接.

基于此，依据预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动五条学习主线，对两个版本教科书的教学内容进行数学史的文本研究，分析数学史料在新版教科书中的分布特征.

图1 两个版本教科书中数学史维度分布

图1是根据《新课标》对新版数学教科书中知识领域的划分，数学史料在不同领域中的数量分布比较.通过对两个版本教科书中数学史所属领域的清晰呈现，便于师生掌握数学史在知识间的逻辑关系.从图1可以计算出整套教科书中人教A版预备知识、函数、几何与代数、概率与统计和数学建模活动与数学探究活动五个主题中分别约为3.8%、11.5%、46.2%、25%和13.5%；北师大版中分别约为8.1%、40.6%、32.4%、16.2%和2.7%.相比较而言，人教A版中数学史料主要侧重于概率与统计主题，另外每一分册在数学建模活动与数学探究活动主题中都有体现；北师大版在函数、几何与代数、概率与统计三个主题中的数学史较多，在数学建模活动与数学探究活动主题中偏少.两套教科书数学史量在必修中较多，其中必修二几何与代数各为9道，其他部分也能在图中显示出来.

2 数学史融入教科书方式的比较分析

两个版本教科书中数学史素材分布于章头语、正文、例题、习题和阅读材料等各个栏目.融入方式主要分为显性和隐性两种方式，如以附加式和复制式这种显性、直接的方式进入，或因教学需要进行适当加工、重构，以顺应式和重构式这种隐性的方式.

研究采用蒲淑萍等[5]建立的分析框架，按照数学史与教学内容的关联程度，将教科书中运用数学史料的方式分为4类：(1)附加式：展示有关的数学家图片，讲述数学故事，或介绍某个数学主题的历史；(2)复制式：正文各栏目中直接采用历史上的数学问题、解法等；(3)顺应式：正文各栏目中对历史上的数学问题、思想、方法进行汇编或根据历史材料编制数学问题；(4)重构式：正文各栏目中借鉴或重构知识(概念、定理等)发生、发展的历史.

2.1 融入方式在教科书中的界定

按照以上分类方式，对两个版本数学教科书中的数学史料进行划分，具体操作如下：

附加式是操作方式简单，比较常见的融入方式，呈现形式主要分布在教科书章头语、正文配图、概念注解或材料补充等环节.这时数学史的融入作为材料补充有益于学生开阔视野，引发学生寻求问题根源的求知欲.例如人教A版必修一中的康托尔与集合论，书中给出康托尔的肖像和生卒年月并配以文字来解释他取得的数学成就和数学家们对他工作的评价；北师大版必修一的欧拉首次提出奇偶函数概念，位于正文中以概念注解的形式解释了奇偶函数的概念是欧拉于1727年提交的论文中首次提出.

复制式属于显性引入，主要是在例题或课后习题中直接设置历史上的数学问题或者在阅读材料中呈现出古人对数学问题的解法来促进学生对知识的理解.这时数学史的融入有助于学生体会古人的数学思想.例如人教A版必修二中的欧几里得《原本》与公理化方法，在阅读与思考板块介绍了欧几里得、《原本》中的公理化方法及公理化方法的作用等，利用数学史引发学生对数学的深度思考.北师大版必修二课后练习题中的已知球体积，求其直径的近似公式问题和刍童问题，这两道练习题目均选自我国古代著名数学著作《九章算术》，引入历史上的数学名题让学生感受历史文化的厚重.

顺应式属于隐性引入方式，通过对历史上的数学问题、思想和方法进行汇编，编制数学问题.这种形式的数学史融入要求既要符合历史客观，同时也要能够起到现实意义.例如人教A版必修二的统计学在军事上的应用——二战时德国坦克总量的估计问题，素材引入是以阅读和思考的形式，内容讲述了用统计学来估计二战时期德国生产坦克的数量，展示了运用统计学及其方法解决实际问题的案例；北师大版选择性必修一没有发现顺应的融入方式，故以选择性必修二的中国古代对数字9的寓意及皇家建筑中的数列问题为例，在正文例题中引入我国古代皇家建筑中与9相关的设计，通过对这一传统思想的介绍,结合以北京天坛圆丘为载体编制数列问题，在题干中以中华优秀传统文化为背景隐性引入来激发学生的爱国之情和民族自豪感.

重构式属于间接引入，融入时的操作难度较大,是对概念和定理的发生、发展的历史进行重构.这种形式是对原有的数学史料进行重构，以便学生更易接受和理解.例如人教A版选择性必修二中斐波那契数列，位于阅读思考板块中，以意大利数学家斐波那契的《算盘全书》中兔子繁殖问题为例引出数列公式，后结合“斐波那契螺旋”弧线和“黄金比例螺旋”形状，重构了这一数学原理的发生、发展过程，体现出数学美的思想.北师大版选择性必修二“微积分的创立与发展”呈现历史上微积分创立的时代背景、创立起始至理论完善，并对牛顿和莱布尼茨各自的工作进行了重构，因此微积分原理的引入属于以重构式方法为主的隐性引入.

2.2 两种版本教科书中数学史融入方式的比较

中国数学教育有着统一性和多样性的特征，即在同一课程标准的规范下存在着不同版本教科书的编写理念[6].通过以上四种数学史融入方式的界定，对两个版本数学教科书中的数学史进行对应划分，得到表2中的数据.

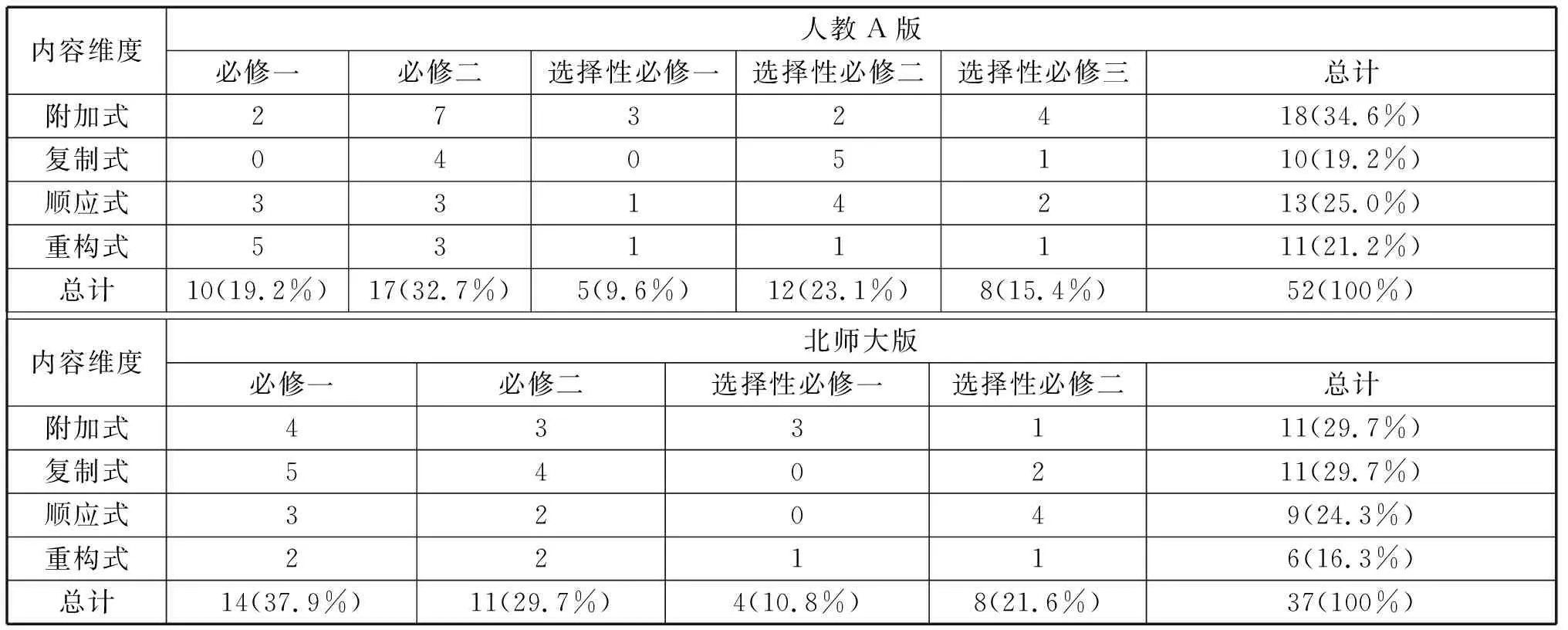
表2 数学史两个版本教科书不同分册中的四种融入方式数量统计

汪晓勤[7]指出利用数学史不同融入方式的分类，可以对数学教科书做出较为合理的分析，并且可以从数学史的视角对数学教科书进行定量和定性的比较研究，其后又强调，数学史的四种融入方式虽然操作难度有区别，但是没有高低之分.根据表2可以看出：首先，两个版本教科书中的数学史在处理四种融入方式时分布均匀，比较稳定.其次，人教A版中附加式运用最多，复制式运用最少，其他两种方式相当；北师大版中附加式和复制式较多，重构式和顺应式较少.最后，需要说明通过比较数学史融入方式能更清晰呈现两者存在的一些客观特征，但同时并不是为了反映出孰优孰劣.

3 结论与讨论

教科书是教学的蓝本，研究教科书是使用好教科书的前提[8].通过对人教A版、北师大版高中数学新版教科书中数学史料的统计和分类、融入方式的比较和分析，得出以下结论：

3.1 数学史料的选取与融入力争贯彻改革理念

新一轮的高中数学课程改革凝练了数学学科核心素养，新版教科书和新高考都将以落实培育学生核心素养为根本目标.数学史料在新版教科书中的运用体现了改革理念：一方面，在融入主题上，新教科书中的数学史料合理地分布在预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动五条知识主线当中，较以往模块化形式的教科书有较大改动，此时一线教师不仅需要掌握知识主题的分布，更要灵活运用知识主题中的数学史料.另一方面，在融入形式上，数学史在数学建模活动和数学探究活动中的融入贯穿必修和选择性必修，有利于学生从数学史视角来发现和提出问题、分析和解决问题，通过动手实践掌握数学史知识，合作交流促进数学核心素养的提升.数学史料的精心选取与融入方式的设计都有利于改革的深入进行.

3.2 两个版本教科书中数学史料的相同与差异

两套教科书在数学史料的使用方面有相同也有差异.相同方面主要体现在经典数学史主题的运用上，教科书不仅仅作为传递知识的载体，更是学生了解数学思想形成过程的窗口，通过设置阅读材料让学生了解数学史，体会数学的发生和发展.教科书的更新虽不断加入一些与新时代背景相符的史料，但教科书肩负着传承数学历史的重担，古今中外典型的数学史料在两套教科书中均得到很好的体现.不同方面在于各自的特色鲜明，例如人教A版设置的“文献阅读和数学写作”板块，紧扣本章的学习内容，提出目标(或主题)、实施建议、参考选题，要求学生撰写文献综述和数学小论文；北师大版在章头语后，设置了与本章内容相关的数学家名言，来引起学生的注意，这都体现出不同版本运用数学史的特色.除此之外，两个版本中融入数学史的数量和方式上也有一些差异.此时需要教师广泛研读，掌握不同教科书对数学史运用的特点，在教学时突出共性和弱化差异，更好地去设计教学过程.

4 启示与建议

面对我国数学文化研究的繁荣景象，数学史在学校数学形态[9]的地位也愈发凸显，数学课程改革也愈发关注数学文化在高中数学教学中渗透的水平和质量.因此，对数学史融入数学教科书也提出了更高的要求，在分析新版教科书中数学史料的基础上，为更好地回应数学课程改革对数学文化教学的要求，更好地利用教科书中精心挑选的数学史，提出以下几方面的建议：

4.1 源头活水：注重教师数学史素养的培养提升

教科书中的数学史应当被看作为冰山一角，需从多方面加强教师的数学史素养，使其自身成为学生获取知识的源头活水.首先，教师自身要改变旧的数学教学观，正视数学史料在教科书中的作用，积极主动通过教研活动、阅读数学史读物、观摩名师讲堂等途径提升自身的数学史素养；其次，学校层面加大投入力度，加强对在职教师的培训，具体如组织教研组开发数学史教学案例或搜集相关资源开展本土化教学等形式；最后，高校严格对师范生的专业化训练，强调职前教师数学史素养的提升，以教科书、试题等为载体进行专题训练、考试测验等活动加强对数学史理论的学习.

4.2 知行合一：提高教师数学史教学的实践能力

教师在使用新版教科书的过程中，要有意识地对比研究不同版本的教科书，关注相同数学史主题在不同版本教科书中的融入形式，进行同课异构来提高自身的数学史实践能力.如人教A版和北师大版中数学史的融入方式整体上保持了一致，但在不同分册中的体现却有差异，教师在把握相关数学史主题分布情况和教科书授课要求后，对比思考不同教科书的特征，尝试通过多次磨课形成自己独特的教学风格.教科书呈现史料素材为教师教学提供了抓手，为学生学习提供了垫板，更重要的是在师生双向互动过程中将书本上冰冷的史学形态演绎为火热的故事情节，教学相长共同探索数学知识背后的故事.

4.3 锦上添花：发挥教科书辅助资料的补充作用

教科书是师生互动的一座桥梁，但不能成为唯一的通道，要充分发挥教科书辅助资料的补充作用.可以利用教科书出版社配套的通读版读物来详细讲解数学知识点的发生发展过程.如果说数学史在教科书中起到画龙点睛的作用，那么相应的数学辅助资料应该能够锦上添花，为学有余力的同学提供深入学习的渠道.教师也可自行搜集相关数学史主题的资料，例如通过数学科普、HPM案例开发、数学史背景试题分析等途径配合教科书中出现的数学史内容，为学生深入理解数学知识、提升数学素服务，进而实现数学史的教育价值.

总之，比较和分析高中新版教科书中融入的数学史，可以提高教师在教学过程中对数学史的敏感度，激发教师进一步思考哪些史料能够融入教科书或教学当中，数学史如何更好地融入教科书或教学当中，不同阶段的学生对数学史的理解程度如何等研究话题.