总体最小二乘在沉降监测数据中的应用研究

胡俊凯，冯杭华

（1.浙江华东测绘与工程安全技术有限公司，浙江 杭州 310014）

随着3S等测绘科学技术的迅猛发展，高精度的测量数据处理技术得到日益重视。考虑到误差会不可避免地存在于观测数据中，在复杂的观测数据中得到高精度的模型估计参数是目前研究的难点[1]。测量平差的基本任务就是处理一系列带有误差的观测值，求出未知参数的最优估值，并评定参数精度[2]。对于Guass-Markov方程的求解，最小二乘法(least squares,LS)是一种经典的方法。然而，在实际建模中，当观测向量包含误差时，由观测向量一次累加而形成的系数矩阵同样包含误差，如果再使用LS求解，计算出的未知参数是有偏差的[3]，全误差模型(errors-in-variables,EIV)将观测向量误差和系数矩阵误差纳入误差模型，其独特的优势已经引起大量学者的研究。总体最小二乘(total least squares,TLS)算法兼顾系观测矩阵和系数矩阵的误差，TLS解被证明具有渐进无偏性[4-6]。本文详细论述了Guass-Markov方程的最小二乘和总体最小二乘解法，并利用路基沉降分析实例，具体分析了2种解法下的预测结果。

1 LS和TLS参数求解

1.1 最小二乘参数求解

Guass-Markov方程L=AX是测量中常用的观测方程，作为经典平差，其处理理论也较为成熟，若仅考虑观测误差的影响，其误差方程为[7]：

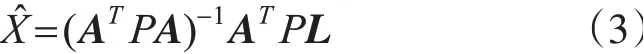
1.2 总体最小二乘求解

最小二乘估计只能保证在某个方向上方差最小，而不能保证在整个方程中最优。当误差方程系数矩阵中含有误差时，直接采用LS方法得到的参数估值不再具有无偏性、方差最小的特性，为了得到最优估值，需要采用顾及系数矩阵误差的总体最小二乘方法。

最小二乘估计方法同总体最小二乘估计方法的最大区别是，总体最小二乘估计方法将系数矩阵作为未知量。全误差EIV模型的思想可以归纳为：不仅白化微分方程中观测向量L包含误差eL，同时系数矩阵A同样包含误差EA[8]。Guass-Markov方程的EIV模型为[9]：

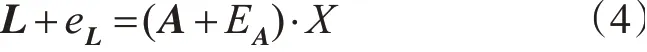
其随机模型为

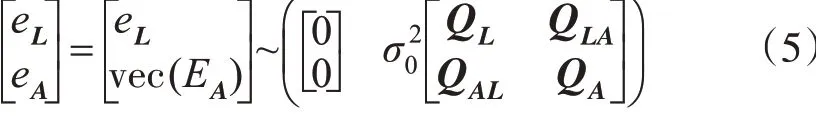
式中，vec(·)表示矩阵拉直运算；vec(EA)表示将改正项EA从左至右逐列拉直的向量；表示单位权中误差；QL表示观测向量协方差矩阵；QA表示系数协方差矩阵；QLA表示观测向量同系数矩阵的误差关系，且，一般情况下不考虑观测向量同系数矩阵的误差关系，即

求解上述方程求解可转化为约束优化问题：

约束条件：L+eL∈Range(A+eA)，式中‖·‖F是矩阵的Fronenius范数。

Euler-Lagrange逼近参数求解方法：

公式(4)可转化为：

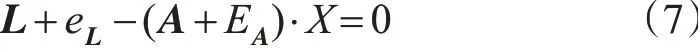
其误差随机模型为：

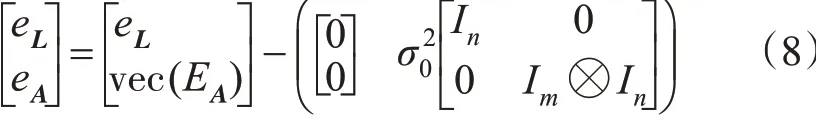
在上式中，符号⊗表示Kronecker-Zehfuss积，总体最小二乘的平差准则为：

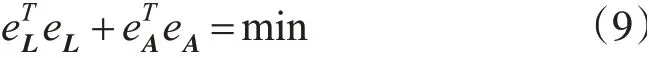
在上述模型中，方程中的参数个数不等于方程个数。为求解模型中未知参数X，需构造Lagrange目标函数：

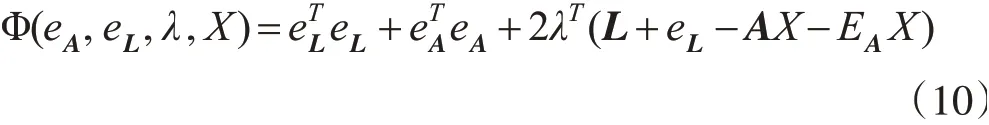
式中，λ为维数为Lagrange因子；其中EA·X=(XT⊗In)·vec(EA)，对其求偏导可得：

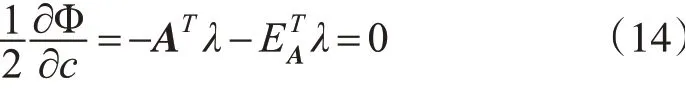
在上述方程中，未知参数个数等于方程个数，方程具有唯一解。将公式11-12代入式(13)整理可以得：

因为原始方程为非线性方程，最为常用的方法为迭代法，具体解算过程如下：

步骤1：通过最小二乘方法计算出参数X的初值

步骤2：Lagrange因子λ。

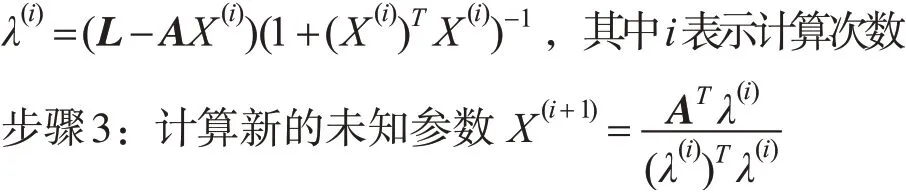
该方法方差为：

则单位权方差的中误差为

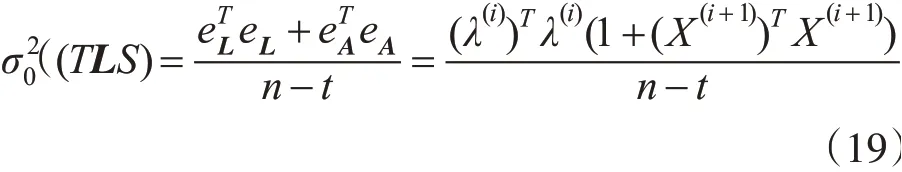
2 工程实例验证

灰色理论对小样本、非等间隔时间序列的处理有一定的优势，它能深入挖掘数据内部隐含的信息，在路基沉降数据处理中具有良好的预测精度[10-12]。为比较灰色理论的最小二乘估计同总体最小二乘估计的预测精度，选用贵广高铁路基沉降数据进行分析。高速铁路建设需严格控制工后沉降，路基沉降观测是确保高速铁路正常运营的重要部分。本高铁路基沉降观测项目应业主要求，在铺轨前6个月对路基进行沉降观测。沉降数据取至路基沉降中后期，监测仪器为TrimbleDi Ni03电子水准仪，并选用配套的铟钢精密条码水准尺，仪器标称精度符合要求，监测标准为国家二等水准要求，监测点上使用沉降板进行覆盖，沉降板埋设于基床底中心，并随基床施工高度增加，接管连续观测。本文以某沉降监测点A为例进行沉降分析与评估，A点监测周期是7 d，监测时间为1 a，共获得了52期观测数据。图1描述了A点本期沉降观测值和总沉降量。在路基沉降评价体系中需要根据观测数据做多种回归曲线，当曲线回归的相关系数不低于0.92时，预测方程才可用于沉降预测。

图1 A沉降点本期沉降观测值和总沉降量变化图

由图1可知，A沉降点在前期下沉速率较快，后期趋于稳定，具有饱和发展过程。受观测条件的影响，观测数据中会包含噪声，因此，在路基沉降观测后期，观测值仍在不断波动。在数据处理中，文章首先对前15期数据进行GM(1,1)模型，采用最小二乘和总体最小二乘估计方法分别求解模型未知参数，然后预测沉降观测数据。前15期的沉降预测数据见表1。

由表1可知，随着路基沉降值得增大，GM(1,1)的预测值同样也增大，并且增大的幅度同路基沉降速率差不多，这说明GM(1,1)用于路基沉降预测是可行的，具有良好的预测精度。在GM(1,1)预测残差中，GM(1,1)中LS估计最大残差绝对值为1.064 mm，而GM(1,1)中TLS估计最大残差绝对值为0.994 mm，小于GM(1,1)-LS估计；GM(1,1)-LS估计和GM(1,1)-TLS估计残差平方和分别为3.602 mm2、3.305 mm2。这说明在此次沉降预测中，GM(1,1)-TLS估计的预测稳定性高。于GM(1,1)-LS估计。图2描绘了2种方法的残差值具体变化。

表1 不同估计方法拟合数据精度对比

图2 GM(1,1)-LS估计同GM(1,1)-TLS预测残差对比图

由图2可知，GM(1,1)-LS估计和GM(1,1)-TLS估计都围着零点上下波动，在前5期中，GM(1,1)-TLS偏离程度大于GM(1,1)-LS，但在后期预测中，预测精度明显高于GM(1,1)-LS。由表1和图2可知，GM(1,1)-TLS估计拟合预测精度要高于GM(1,1)-LS估计，采用TLS估计，预测稳定，预测精度高。路基沉降各期预测值，如图3所示。

由图3可知，GM(1,1)-LS估计和GM(1,1)-TLS估计在后期都趋于稳定，同路基先沉降速率加快，之后逐渐减慢，最后趋于稳定的变化趋势相符，这说明GM(1,1)预测方法可以应用于路基沉降预测。在路基沉降后期阶段，GM(1,1)-LS预测值同观测值的偏离程度大于GM(1,1)-TLS预测值，这说明对GM(1,1)白化微分方程采用总体最小二乘估计预测精度高于最小二乘预测，因此，兼顾系数矩阵和观测向量误差的总体最小二乘估计方法有利于提高预测精度。综上分析可知，GM(1,1)总体最小二乘估计方法预测稳定，预测精度高，可以广泛应用于路基沉降预测。

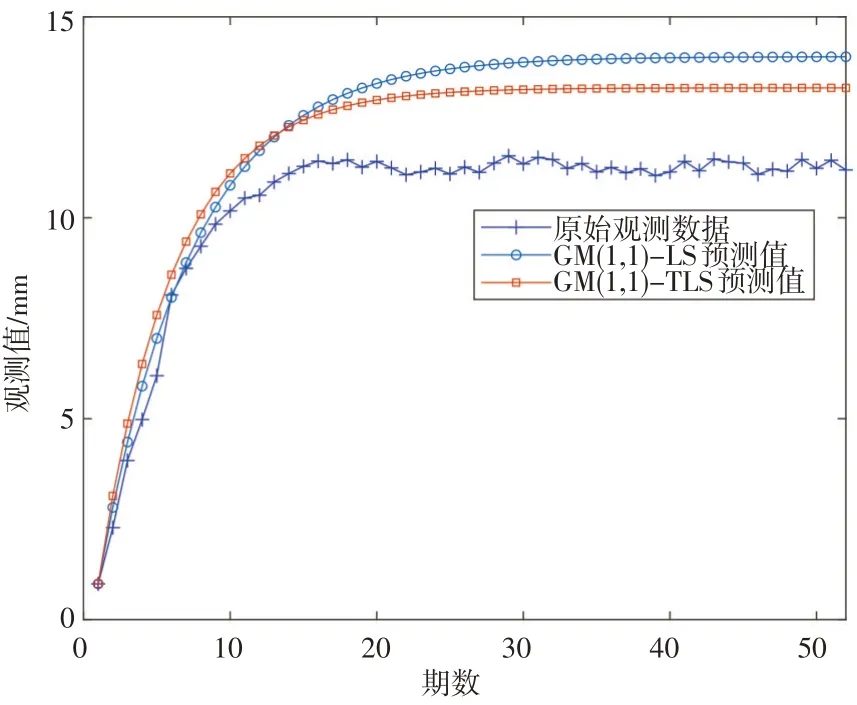
图3 GM(1,1)-LS，TLS估计方法预测数据对比图

3 结语

总体最小二乘方法是最近出现的可以同时顾及系数矩阵误差额观测值误差的一种数据处理方法，在信号处理、测量平差等领域得到了广泛的研究和应用。目前，总体最小二乘方法已经广泛应用于坐标转换、大地测量反演、工业测量、GPS数据处理、摄影测量、室内定位、天文学等。通过路基沉降预测的实例，结果表明总体最小二乘算法在路基沉降预测中也有较好的应用效果。