混凝土坝洪水漫顶生命风险评价

李宗樾，余 雷，胡泽林，程 井

(1.贵州省大坝安全监测中心，贵州 贵阳 550002；2.河海大学 水利水电学院，江苏 南京 210098)

截至2019 年底，中国已建成各类水库超过98 000 座，是目前世界修建水库最多的国家[1-3]。水库在发挥巨大社会效益和经济效益的同时，也存在不可规避的风险[4]。为了尽可能减少水库大坝失事带来的损失，大坝风险管理显得格外重要。我国自从1954 年有较为完整的溃坝纪录以来，随着水库的运行管理等各项工作的不断完善，大中型水库的溃坝事件随时段剧减。1954—2018 年水库共溃坝3 541 座[5]，其中1954—1982 年共溃坝3 115 座，年均溃坝107.4 座；1983—1999 年共溃坝332 座，年均溃坝19.5 座；2000—2018 年共溃坝84 座，年均溃坝4.4 座，年均溃坝概率降至0.45×10-4[4-8]。

导致溃坝的原因主要包括洪水漫顶、大坝质量问题及管理不当等，其中洪水漫顶占50%以上[6]。特别是近年来，全球气候变化导致的极端天气频发，超标洪水频率明显上升，给水库大坝带来了严峻挑战[9]，如2020 年乌兹别克斯坦的萨尔多巴水库溃坝，以及美国密歇根州的伊登维尔大坝及桑福德大坝溃坝[5]，这些溃坝事故造成严重的经济和生命损失。如何合理评估库坝的各类风险，成为大坝运行维护的重要内容[4]。

优质实体混凝土坝可以长期服役，但在遭遇超标洪水且泄流能力不足时，仍存在较大的洪水漫顶及溃坝风险[10-11]。坝前最高水位与入库洪水息息相关，而传统的设计洪水频率分析通常为单一变量分析，无法全面反映洪峰与洪量之间的相关关系。基于Copula 函数的多变量设计洪水频率分析能更全面地描述洪水的内在规律[12-16]。将多变量洪水分析引入洪水漫顶生命风险评价，更贴合洪水发生及漫顶的实际情况。本文以贵州某水电站为例，研究混凝土坝遭遇特大洪水并发生漫顶情况下的生命风险评价方法，基于Copula 函数构建洪峰与洪量关系，并采用MC 抽样方法通过三点式变倍比放大法得到年最大入库洪水过程线概率序列；依据随机生成的洪水过程线模拟洪水淹进过程，进行生命风险评估，并判定风险的可接受程度。

1 混凝土大坝安全评价的过程及原理

1.1 拟定年最大入库洪水过程线概率序列

三点式变倍比放大法，是一种同时考虑峰量、利用典型洪水过程线推求设计洪水过程线的放大方法，对多变量洪水分析中用到的变倍比放大法[13-15]的前后收敛性问题进行了改善，见式（1）～（4）。与以往洪水放大法采用单变量进行分析不同，该方法基于Copula 函数进行多变量洪水分析，可同时考虑洪峰、洪量及典型洪水过程线形状对设计洪水过程线的影响。

式中：Qmax和QDmax为模拟洪水过程线和典型洪水过程线的最大洪峰流量；Q和QD为模拟洪水过程线和典型洪水过程线某一时段的平均流量；Qt和QD(t)为t时刻模拟洪水过程线和典型洪水过程线对应流量；QD(0)和QD(T))为典型洪水过程线的初始流量和结束流量；tQDmax为典型洪水过程线最大洪峰流量相应时刻。

Copula 函数可以连接多个随机变量的边缘分布来构造联合分布。近年来在水文领域经常使用的3 种单参数二维Archimedean Copula 函数[16]见表1。基于Gumbel-Hougaard 函数构建的洪峰与洪量关系，通过MC（Monte Carlo method）法随机生成较大组数的洪峰与洪量。利用生成的洪峰、洪量及典型洪水过程线通过三点式变倍比放大法得到年最大入库洪水过程线。就水库大坝工程防洪安全而言，坝前最高水位起着决定性作用，将坝前最高水位的重现期看作设计洪水过程线的重现期。用年最大入库洪水过程线序列进行调洪演算得到坝前最高水位序列，进一步可得到坝前最高水位的累积频率。将坝前最高水位与年最大入库洪水过程线相对应，便可得到年最大入库洪水过程线的累积频率，即年最大入库洪水过程线发生概率。

表1 Archimedean Copula 函数参数θ 与Kendall 相关系数τ 的关系Tab.1 Relationship between Archimedean Copula function parameter and Kendall rank correlation coefficient

1.2 大坝洪水漫顶生命损失评估

文献[17]通过对8 座水库溃坝洪水严重性的分析，并结合我国历史溃坝生命损失的主要规律，提出适合我国水库溃坝实际情况的生命损失模型。模型主要考虑3 个部分：风险人口PAR、风险人口死亡率f及溃坝对下游造成的严重性系数α，LOL=RARfα，RAR=mPSP，α=m1+bm2，其中：mP和SP分别为下游受灾地区的人口密度和淹没面积；m1和m2分别为生命损失的直接和间接影响因素的严重性影响因子，文献[17]定性给出了影响因素的严重性程度判别建议标准，m1/m2≤1；b为生命损失间接影响因素的严重性程度影响因子系数，0＜b＜1，采用0.25；f为风险人口死亡率，主要考虑溃坝洪水严重性、警报时间和风险人口对溃坝洪水严重性理解程度3 个影响因素，文献[17]给出了适合我国水库溃坝的风险人口死亡率建议表。

利用1.1 节得到的年最大入库洪水过程线序列作为HEC-RAS 软件的基础数据，进行大坝洪水漫顶模拟演进，并对洪水漫顶后对下游造成的生命损失进行评估。

1.3 生命风险标准制定

ALARP (As Low As Reasonably Practicable)是目前国际公认的风险准则[6,18]，依据可接受风险水平与可容忍风险水平将风险划分为可接受风险、可容忍风险和不可容忍风险3 个区域，这两个风险水平即为所谓的风险标准。F-N线法是确定风险标准的主要方法之一，N为死亡人数，F为N的累计频率限制曲线。式（5）表示F的超过概率与死亡人数N之间关系，通过在双对数坐标系中确定起点位置、斜率和极值线来描述F-N标准线。

式中：FN(x)为年死亡人数小于x的概率分布函数；C为常数；n为标准线的斜率。

生命风险标准的构建与社会、环境及当地的政治、经济、文化等因素有关，不同国家地区考虑的侧重点有所不同。2006 年李雷等[6]遵循ALARP 准则，依据我国年均溃坝率及溃坝人数的估算，提出我国生命风险标准的F-N线建议图。2015 年李宗坤等[18]结合我国水库大坝安全现状及其他行业的风险标准情况，对F-N标准线的参数取值进行了更新：建议对水库大坝可容忍风险标准的C值取10-2，可接受风险标准的C值取10-3；将大中型水库归属于风险厌恶型（n值取2），小型水库归属于风险中立型（n值取1）；同时考虑了中国大坝事故概率和中国可靠度标准分别进行极值线的计算，并取较小值作为标准，见图1。

图1 大中型及小型水库社会生命风险标准Fig.1 Social life risk criteria for large and medium-sized reservoirs and small reservoirs

2 工程应用

某水电站水库位于贵州省黎平县境内，工程等别为Ⅲ等，主要建筑物为3 级。水电站原大坝为抛物线双曲拱坝，坝顶高程288.8 m，最大坝高65.8 m，坝顶设置0.9 m 高防浪墙。2016 年因调度不当发生漫坝事故，坝前水位达到历史最高洪水位290.1 m，高于防浪墙顶0.4 m，造成较大经济损失和社会影响。2019 年针对工程存在的抗洪能力不足问题进行了除险加固，拆除原有溢流堰顶胸墙，对大坝坝顶上游面防浪墙进行加高处理，增强大坝的抗洪能力。

2.1 拟定洪水过程线序列

根据1964—2015 年的实测水文数据，结合调查所得历史洪水，推得该水电站的设计洪峰及洪量。采用P-Ⅲ分布曲线分别描述洪峰流量边缘分布u和最大3 日洪量边缘分布v。构建P-Ⅲ分布的相关系数结果为：最大洪峰流量q为693 m3/s，变差系数Cv为0.68，偏差系数与变差系数的比值Cs/Cv为4.5；最大3 日洪量w为0.34 亿m3，Cv为0.65，Cs/Cv为4.0。

利用表1 的Gumbel-Hougaard Copula 函数构建洪峰流量与最大3 日洪量二者边缘分布的联合分布C(u,v)，其中τ=0.92。基于MC 法在（0,1）区间随机生成10 万组相互独立且均匀分布的u与条件概率Pv|u，利用式（6）得到10 万组符合C(u,v)分布的(u,v)见图2。利用反函数u-1、v-1推得10 万组(q,w)，随机生成的q与w的P-III 分布见图3～4。利用三点式变倍比放大法式（1）～（4）对典型洪水过程线（图5）进行放大模拟得到10 万条年最大入库洪水过程线。基于所有年最大入库洪水过程线对除险加固后的水库进行调洪演算，得到坝前最高水位累积频率曲线如图6，相应可得年最大入库洪水过程线发生概率。

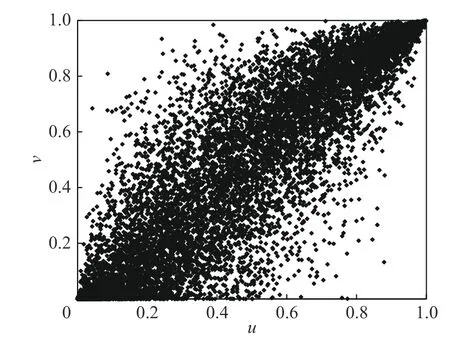
图2 (u,v)抽样分布Fig.2 Sampling of (u,v)

图3 随机生成的洪峰q 的P-III 分布Fig.3 P-III distribution of randomly generated flood peak q

图4 随机生成的洪量w 的P-III 分布Fig.4 P-III distribution of the randomly generated flood volume w

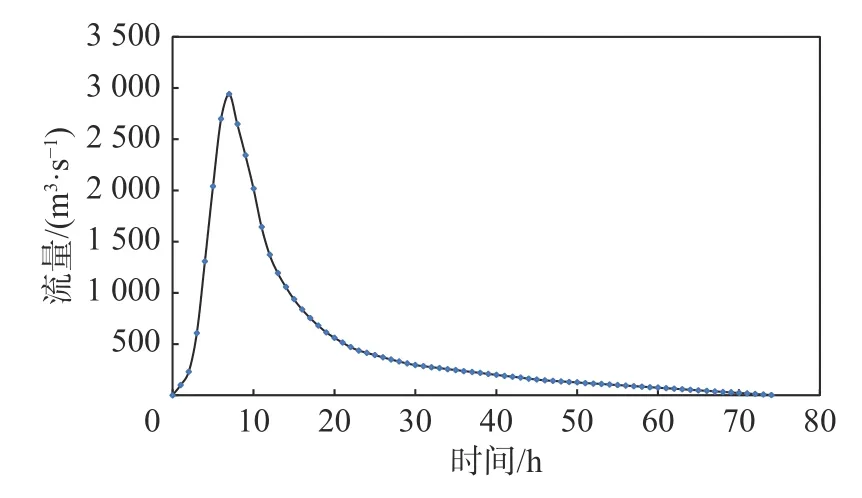
图5 典型洪水过程线Fig.5 Typical flood process line

图6 坝前最高水位累积频率曲线Fig.6 Cumulative frequency curve of highest water levels in front of the dam

式中：Pv|u为条件概率；C(u,v)为双变量Copula 函数。

2.2 大坝洪水漫顶生命风险评价

工程所处位置偏僻，受工程规模及勘测精度等客观条件限制，对下游3 个村镇的高程取平均海拔高程，人口采用均匀分布，具体信息见表2。

表2 各村镇信息Tab.2 Information of villages and towns

利用HEC-RAS 软件对上游水库、拱坝及下游可能的淹没区域进行模拟。上游水库初始水位设置为280 m（溢流堰堰顶高程），下游区域以河床起算，模拟时间设置为2050 年6 月10 日8:00—2050 年6 月13 日11:00，入库洪水的模拟在随机生成的年最大入库洪水过程线序列中选取1 条输入。

此次模拟的年最大入库洪水过程序列有10 万条，无法逐条进行模拟，但由大坝洪水漫顶造成下游海拔相对较高地区淹没的情况为极值事件，只需对几个极小概率的洪水过程线的情况进行洪水模拟演进。图7 为HEC-RAS 输入概率为1.0×10-5的年最大入库洪水过程线时（本次模拟中发生概率最小的年入库洪水过程线）下游最大淹没水深示意。从图7可见，下游村落中只有最靠近大坝的SJ 村出现被洪水淹没的情况。模拟的目的是为了进行生命损失的评估，则此次只需要对能淹没SJ 村的年入库洪水过程线进行模拟。

图7 概率10-5 的洪水漫顶工况的下游最大淹没水深示意（2050-06-10T15:43）（单位:m）Fig.7 Schematic diagram of the downstream maximum submerged depth under flood overtopping condition with probability of 10-5 (2050-06-10T15:43) (unit:m)

在SJ 村区域内，选取具有代表性且尽可能均匀分布的5 个测点，将人口均分在各测点上，从出现概率为1.0×10-5的年最大入库洪水过程线开始，概率从小到大分别输入HEC-RAS 软件中进行洪水模拟演进。对HEC-RAS 洪水模拟演进的结果，查看各测点洪水淹没水深和淹没洪水流速（图8～9），最终用洪水严重性即最大淹没水深与流速的乘积值来反映SJ 村的整体受灾严重性，结果见表3。当模拟输入的年最大入库洪水过程线概率大于等于7.0×10-5时，SJ 村不再出现洪水淹没，则更大概率的洪水过程线无需进行模拟。

图8 SJ 村淹没水深过程线Fig.8 Process line of submerged water depth in SJ village

根据文献[17]建立的生命损失模型，将人口集中于5 个测点上，各测点的人数均分为230 人。SJ 村风险人口死亡率f的取值，由SJ 村村民对溃坝洪水严重性理解清楚（SJ 村地处多库坝的省份）、漫顶洪水属于完全报警的情况（HEC-RAS 洪水模拟演进结果显示，从洪水开始漫顶到SJ 村出现淹没的时间间隔为2.0～2.5 h）、SJ 村的受灾严重性（表3）3 个方面，根据文献[17]的风险人口死亡率建议表进行取值。最终得到各极小概率洪水的生命损失及死亡率，结果见表3。

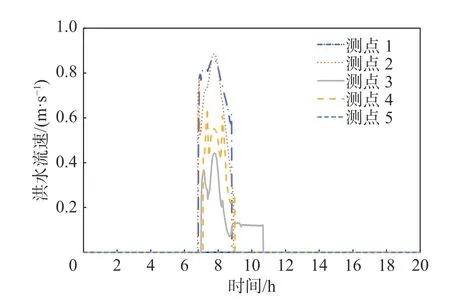
图9 SJ 村淹没洪水流速过程线Fig.9 Process line of flood velocity in SJ village

由于模拟的最小概率洪水过程线对应的坝前最高水位已经达到设置水位条件的最大边界，对于超出边界水位，例如超出水位-库容曲线范畴，无法探究规律，一般认为发生概率为零。由表3 可以看出，经除险加固后的拱坝的洪水漫顶生命风险超过1 人的概率为2.5×10-9～8.0×10-9。该水电站为中型水库，对比图1 大中型水库社会生命风险标准，可见除险加固后的水电站洪水漫顶生命风险处于可接受范围。

表3 SJ 村受灾严重性Tab.3 Severity of the disaster in SJ village

3 结语

本文提出了一种洪水概率序列生成-漫顶洪水演进-下游生命损失评估的混凝土坝漫顶生命风险定量评估方法。该方法基于Copula 函数与三点式变倍比放大法进行设计洪水多变量联合分析，可考虑洪水特征量间的相互关系，得到的年最大入库洪水过程线发生概率序列更加符合洪水内在规律；漫顶生命风险定量评估与符合我国现状的风险标准共同构成了完整的混凝土坝生命风险评价体系。以贵州省某拱坝为例进行了分析评估，结果表明，大坝加固后洪水漫顶对下游村镇造成生命损失的风险较小，属于社会可接受的范围。