冰波运动特性及盖移质输冰能力研究

罗红春，冀鸿兰，牟献友，郜国明，张宝森

(1.内蒙古农业大学 水利与土木建筑工程学院，内蒙古 呼和浩特 010018；2.黄河水利科学研究院，河南 郑州 450003)

冰塞是寒区河流一种常见的水力现象，也是引发凌汛洪水的主要致灾因子，易形成于水库回水末端、弯道、比降由陡变缓的河段等位置[1]。自龙羊峡、刘家峡水库联合调度以来，黄河宁蒙河段冰坝的出现频次显著降低，冰塞事件反而频发，凌汛致灾模式主要转变为冰塞洪水[2-3]。目前已开展了大量关于冰塞形成、堆积演变的模拟及试验研究[4-9]，这些代表性成果有力地推动了江河冰塞的研究进展，然而，当前却鲜有相关研究关注水内冰颗粒的运动特性及输冰能力。河流冰盖形成后，流动的冰花通过下潜会浮在冰盖底部，逐渐发展稳定，形成特殊的类似于沙波形态的现象——冰波，这是冰塞的另一种体现。早在20 世纪60 至70 年代，Pariset 等[10]便提出冰盖下的水内冰颗粒（盖移质形式）与河床表面的泥沙颗粒（推移质形式）具有相似的运动特性；Starosolszky[11]建议使用类似泥沙的推移质公式描述冰盖下的输冰，之后，部分学者基于此设想开展了相关的讨论与试验[12-14]，并在室内发现了该试验现象；Shen 等[15]通过推移质泥沙输移理论，首次提出了“输冰能力”的概念。但真正利用泥沙输移理论对冰下盖移质输移进行具体分析的研究仍非常少见，更缺乏对盖移质群体运动特征的研究。冰波运动过程与冰塞的形成演变及输冰能力息息相关，对封、开河预报及凌汛预防具有重要意义[16-17]。Wang 等[18]结合理论分析与物理模型试验，开展了冰波运动的研究，明确了冰波形成及消失的水力条件，并给出了盖移质输冰能力的计算公式，但没有给出冰波运动的控制方程，且在冰波波高的计算过程中未考虑冰层的影响（输冰率误差的来源之一）。

因此，为进一步研究冰波运动特性及盖移质输冰能力，在Wang 等[18]研究的基础上，借鉴泥沙输移理论，通过类比推移质运动，从力学角度出发，建立冰波波高与波长的控制方程，分析波高与波长的演变规律及变化过程中涉及的影响因素，深化对冰波运动特性的理解。同时，考虑冰层厚度的影响，改进原有输冰率公式，提升其普适性及精确性；构建盖移质输冰能力与水流强度的本构关系，增强对江河冰塞形成及堆积演变过程的辨识能力。

1 冰波形成及演变机理

1.1 盖移质运动特性

冰波是冰下盖移质冰颗粒所做的集体运动，其形成过程与沙波类似，对盖移质与推移质进行力学分析（图1），显然，二者运动特征具有明显的相似性：一定水流条件下，盖移质贴近冰盖底面向下游输移，推移质则贴近床面向下游输移。区别在于：泥沙颗粒密度大于水，冰颗粒密度小于水，盖移质颗粒更容易起动；盖移质颗粒级配明显大于推移质；盖移质与推移质的垂向受力部分相反，即推移质颗粒受拖曳力、上举力及重力，而盖移质颗粒受拖曳力、浮力及重力（不考虑粒间离散力与黏结力）；盖移质集体运动形成的冰波可能出现整体移动，推移质则有一厚度相对稳定的静态层；冰波波长相较于沙波会更长，冰波波高变幅受水流强度改变会更为明显[18]。与推移质运动划分一样，盖移质运动也包含跃移质运动、接触质运动和层移质运动。

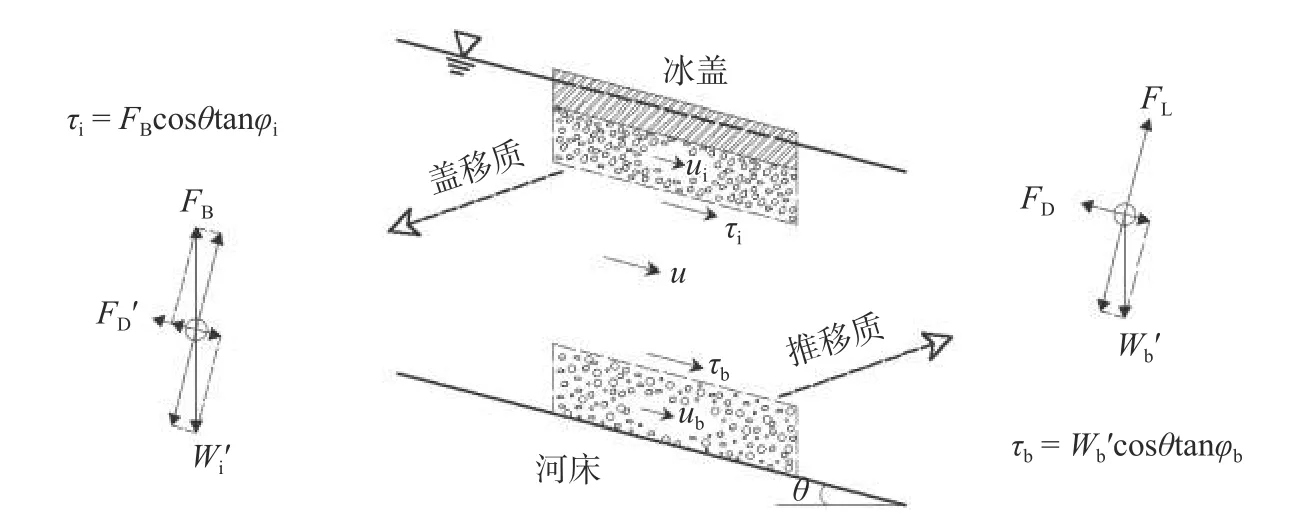
图1 推移质与盖移质受力Fig.1 The stress process of bed load and cover load

基于推移质与盖移质受力的相似性，从泥沙运动的物理力学角度切入，利用Bagnold 的能量观点对盖移质输移进行研究。对推移质而言，因搬运固体颗粒在单位时间内所消耗的能量（对泥沙运动做功）=水流在单位时间内所损失的势能（水流提供的功率）×效率，即：

式中：FB为单位面积盖移质所受的浮力（N/m2）；为盖移质平均流速（m/s）；φi为冰颗粒间的动摩擦角（°）；τi为冰盖下表面的剪切力（N/m2）；ei为水流搬运盖移质的效率。即：输送盖移质运动所做的功是水流在冰盖底部的切应力与流速和效率的乘积。

由于国内外对盖移质运动的研究涉及极少，故对盖移质输移的理论研究还不成熟，而在推移质运动的研究方面则已形成了较为系统完善的理论，因此，借鉴泥沙输移理论分析盖移质运动特性和输冰能力时，需厘清推移质运动特征及其应用层面。对推移质运动的应用主要体现在输沙率上，根据研究方法的不同，形成了几个典型学派[19]：以试验为基础的Meyer-Peter 公式；以力学分析为基础的Bagnold 公式；以概率论为基础的Einstein 公式；还有综合各家研究方法衍生出来的Engelund 公式、Yalin 公式、Ackers 及White 公式等。

尽管不同学派的推移质输沙率公式具有不同的表现形式，但其统一式均体现推移质输沙率与水流条件满足一定的函数关系，亦即都可转化成无量纲推移质输沙强度与水流强度之间的函数关系[20]：Φ=f(Θ)。因推移质与盖移质力学与受力与运动的相似性，无量纲盖移质输冰强度Φi与水流强度Θi之间也应具有如下的函数关系：Φi=f(Θi)。

1.2 冰波形成机理

冰波是冰盖底部的一种冰面形态，反映冰底面的起伏特征。研究冰波的形成机理对分析输冰能力、冰塞阻力及冰塞的堆积演变具有重要意义。冰波的形成及发展条件与沙波类似，均与水流强度Fr有关，当水流强度低于下临界Frmin时，冰波不出现，大于上临界Frmax时，冰波消失，故其形成条件应处于两临界值之间。冰波在形成过程中，与沙波一样，理论上会经历平整-冰纹-冰垄-动平整-逆行冰波等过程。由于冰波演变过程处于动态变化，冰波在各种形态间的切换很快，各阶段的冰波变化不易被观测，但其主要表现形式为形态较稳定的冰垄或逆行冰波。

隋觉义等[21]通过研究讨论，给出了一项关键水力参数值，即水浸冰临界弗劳德数Frc=0.28。当Fr＜Frc时，水内冰的堆积状态为冰垄-动平整的过渡阶段；当Fr=Frc时，为动平整阶段；当Fr＞Frc时，为逆行冰波状态；当Frmin＜Fr＜Frmax时，可将冰波运动发展过程分为以下3 个阶段：（1）发育期。水内冰颗粒在拖曳力与剪切力作用下开始在冰盖底部进行堆积，形成初生冰波；随着上游来冰量增加、Fr增强及水流对初级冰波产生的摩阻作用，冰波逐渐发展，表现为波高增高、波长增长，冰波波峰所在断面流速增加。（2）稳定期。Fr进一步增强，冰波形成较为稳定的冰垄，当水流强度恰好能促使冰颗粒脱离冰波表面时，即达到盖移质起动流速，此时冰波发展达到极限。（3）消亡期。继续增加水流强度，盖移质起动概率显著增加，大量盖移质逐渐转换为“悬移质”，冰波逐渐消亡，表现为波高减小、波长缩短，在达到上临界水流强度时，冰波消亡，冰颗粒以“冲泻质”形式整体向下游移动。实际中，冰波形成的3 个时期一般是交替叠加而非严格依顺序出现。虽然Fr对冰波形成影响很大，但却不是唯一的影响因素，流速分布、水流紊动能、边界条件及冰颗粒所受剪切力等均会对冰波的形成起到促进或抑制作用。

1.3 冰波运动特性及控制方程

与沙波运动类似，迎流面冲刷、背流面淤积是维系冰波发展的主要形式。理论上，当冲刷的水内冰颗粒绝大部分以盖移质形式运动时，盖移质以爬坡形式促进冰波下移运动中的增高增长，冰盖底面逐渐粗糙，此时冰波往往是处在发育期；冰波形成后，水流强度在一定范围内增加时，冰波会维持一定的形态与大小并以某一固定运动周期而逐渐趋于稳定；当水流强度超过某一临界值后，波峰处水流流速达到极值，冰波出现“削峰”，伴随着粒径小的冰颗粒以喷射的方式脱离冰波表面、粒径大的则以蠕移或滚移的方式在波谷处落淤的粗细分选现象，绝大部分冰颗粒是以“悬移质”形式运动，聚集体坍塌，冰波逐渐消亡，冰盖底面趋于平整。故冰波波高或波长随水流强度的变化规律是先增加而后减小的非单调增加变化特点，这也是冰波在不同水流条件下形态不同的原因。因此，可认为迎流面上冰水运动表征的是冰波反作用于水流的一面，体现盖移质输冰强度的大小，迎流面上冰水运动程度是影响冰波运动形式和盖移质输冰率的关键，当需要研究盖移质输冰能力的特性时，选择冰波迎流面上的水体为隔离体更合适；而背流面上的冰水运动恰好反映了水流塑造冰波形态的一面，冰波背流面上的冰颗粒淤积程度是决定冰波运动形式的关键，其淤积水平能较好地反映出冰波尺度的变化，故对冰波运动特性的研究，选择冰波背流面作为研究对象更具有代表性。

选定任一单个冰波的背流面（图2），实线和虚线分别表示t1和t2时刻冰波的运动状态。在冰波波谷处，冰颗粒处于停滞状态，因此认为该区域的流速为盖移质临界起动流速，对应临界弗劳德数。

图2 单个冰波运动特征Fig.2 Characteristics of individual ice wave motion

借鉴泥沙运动力学中的沙波运动理论[22]，分别建立冰波运动的微能量及微动量方程[23-24]，进一步分析冰波的运动特性。

1.3.1 微能量方程的建立 由于目前对冰盖下水流的判定是有压流还是无压流尚无明确定论，部分学者认为其属于浅度有压流[25]，现实很难去量测冰下水压，为简化此项因素，本文以无压流处理。以床面为基准面，则t1时刻AA-BB断面与t2时刻A'A'-B'B'断面的能量方程分别为：

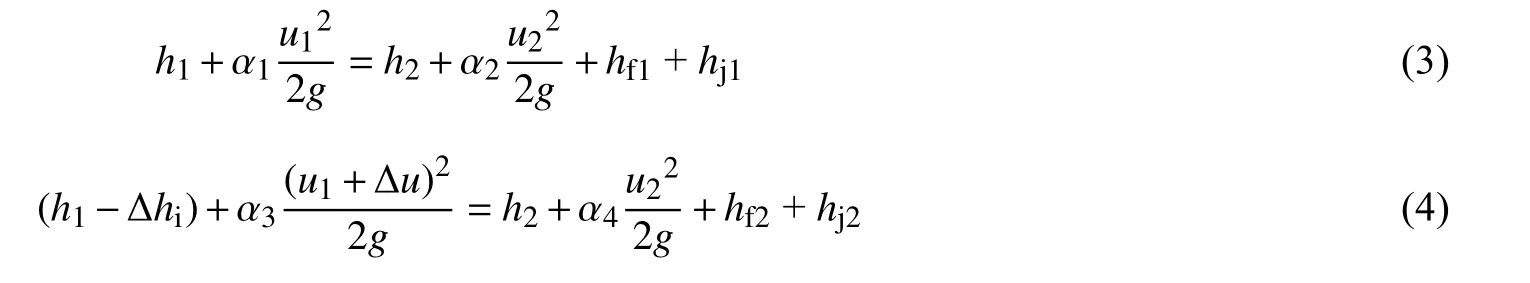
式中：h1、h2分别为冰波波峰与波谷距河床的高度（m）；u1、u2分别为冰波波峰与波谷所在断面的平均流速（m/s）；Δhi、Δu分别为波高与平均流速在Δt时间内的增量（m/s）；g为重力加速度（m/s2）；hf1、hf2、hj1、hj2分别为AA-BB断面与A'A'-B'B'断面的沿程水头损失与局部水头损失（m）；α1、α2、α3、α4为动能修正系数，均取为1。

利用式（4）减式（3），忽略方程中高阶小量，并令：x=λ2/h2，y=hi/h2，uv=u1/u2，Δx=Δλ/h2，Δy=Δhi/h2，（盖移质临界起动弗劳德数）。可得：

对上式左右两边取极限，可得：

1.3.2 微动量方程的建立 由水流连续方程h1v1=h2v2可得h2/h1=u1/u2=uv。考虑冰波背流面的受力，包括：

式中：γ为水的重度（N/m3）；B为河宽（m）；ti为冰厚（m）；Δ 为稳定盖移质层厚度（当形成稳定冰塞时，代表平衡冰塞体厚度）（m）；hi为冰波波高（m）。

式中：τ0为冰面切应力（N/m2）；ξ为修正系数。

式中：CD为冰波形状阻力系数；kD为作用水流的面积系数。

将各力的表达式代入式（11），可得：

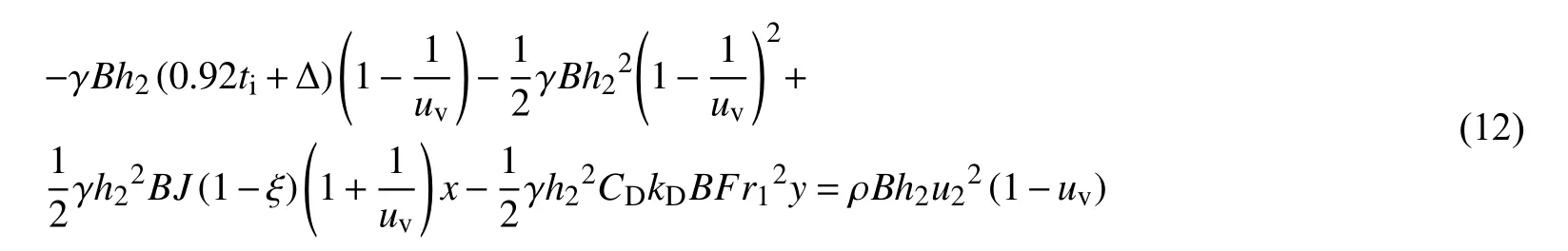
化简，得t1时刻微动量方程：

同理，t2时刻微动量方程：

将式（14）减式（13），忽略方程中的高阶小量，整理得：

对式（15）左右两边取极限，得：

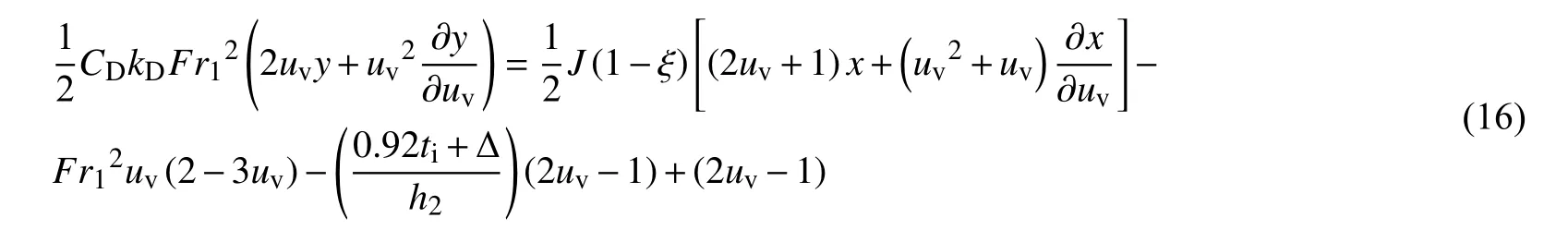
将式（6）与式（16）改写为全微分形式得：

式（17）和（18）即为冰波运动的控制方程。

将冰波运动方程进一步改写成积分形式：

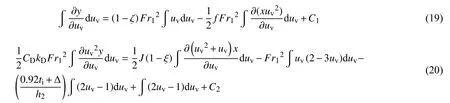
由初始条件：uv=1 时，x=y=0，可解得积分常数：，C2=0。则进一步有：

将x=λ2/h2，y=hi/h2代入以上两式，联立方程后解得：

方程（23）与（24）即为冰波运动尺度与水流强度之间的函数关系，与沙波运动的表达式相似。这说明冰波运动过程中波高与背流面波长的变化受水流强度、水深、冰下阻力等因素的综合影响。

2 盖移质输冰能力

取任一单波迎流面进行分析，选取冰波波谷断面与冰波波峰所在断面间的部分为控制体。参考泥沙连续方程，则水内冰颗粒的连续方程为[19]：

式中：qi为以重量计的盖移质单宽输冰率（N/(s·m)）；ηi为冰波在各点的高度（m）；γi为考虑孔隙在内的盖移质单位重度（N/m3）。

与沙波运动类似，假定冰波在运动中形状基本不变，则：

式中：ui为冰波波速（m/s）。

联立式（25）与（26），得两个相邻冰波波峰之间范围内的单宽盖移质输冰率：

式中：αi为冰波形状系数，q0为冰波波谷处的单宽盖移质输冰率，可忽略不计，则：

方程（28）中的未知参数为冰波波高及波速，输冰率的计算中，选取冰波的迎流面更为合适，故以冰波迎流面为研究对象进行波高计算。为简化影响因子，短距离河段忽略比降影响（则沿水流方向的水体质量力为0，同时避免计算过程中迎流面波长的引入）。

2.1 冰波波高的计算

简化后相对波高为：

冰波波高的表达式为：

2.2 冰波波速的计算

冰波波速关联诸多物理量，其具体的函数关系尚不明确。目前，波速公式结构的型式基本均为经验或半经验式，因此，需结合理论分析与试验进行波速与各参数间具体的描述。参考Wang 等[18]的研究，可知冰波波速受来冰量Qi、来水量Q、河宽B等因素的影响，各因素间的函数关系可表达如下：

除去非独立量及次要量，由量纲分析可得：

则单宽盖移质输冰率为：

当不考虑冰盖影响时，即方程中涉及的A1项，式（36）即等同于Wang 等[18]的研究结果。当水深远大于冰厚时，H≈h2，则有Fr1≈Fr。

当冰波波高的数量级小于等于冰厚时，利用Wang 等[18]的公式计算输冰率会出现较为明显的误差。因此，本文修正的公式更为准确，普适性更强，能反映输冰率与水流强度的正向变化过程，当然，此式在野外应用时也会受到不确定性限制。此外，Wang 等[18]的研究中，发现qi约正比于u3.7，与qb正比于u4接近（预估a2的范围应为1.5～2.0）。可见，水流流速/强度是影响输冰率的主要因素之一，来冰量、相对高度等因素对输冰率均有一定影响。

将式（36）进行转换，可进一步改写为：

式（37）即类同于Bagnold 推移质输沙率公式，印证了前文的设想。水流对盖移质的剪切力τi=γiHJ；水流搬运盖移质的效率

将盖移质输冰率公式转换成无量纲盖移质输冰强度与水流强度的函数关系，有：

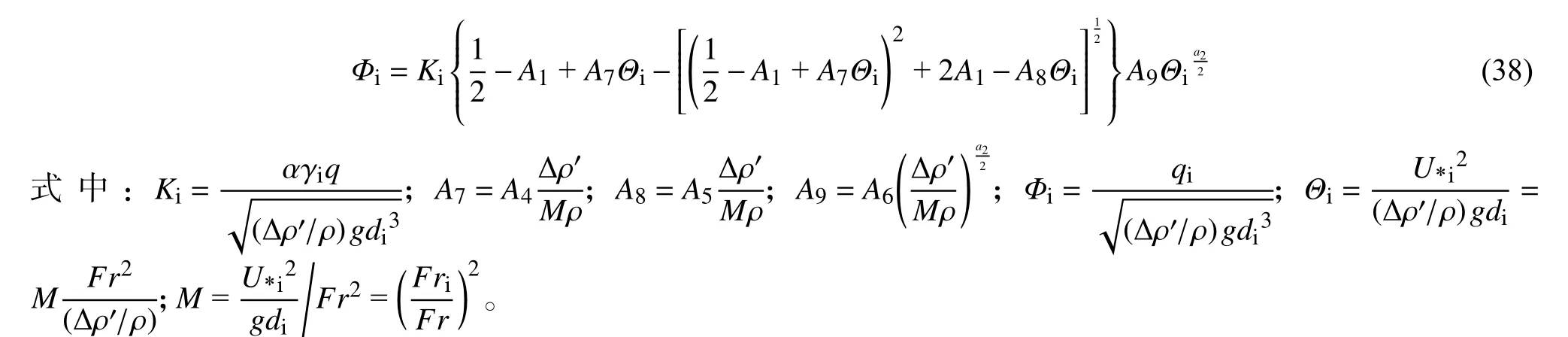
可见，无量纲盖移质输冰强度与水流强度呈现非线性的复杂函数关系，大体上，，Θi∈结果与前文假定的Φi=f(Θi)一致，且与Shen 等[15]的试验拟合结果接近。

汪德胜等[12]指出，借鉴轻质推移质计算公式，Bagnold[26]和Luque 等[27]推移质公式可用于估算稳封期的输冰流量，本文得出的输冰率公式同Bagnold 推移质输沙量公式具有相似性，与汪德胜等[12]的研究结果一致。

3 结语

在前人理论研究的基础上，借鉴泥沙输移理论，分析了冰波运动特性，从理论层次推求了冰波波高与波长（背流面）的控制方程；同时，考虑冰盖的影响建立了全新综合的盖移质输冰率表达式，进一步推导了无量纲盖移质输冰强度与水流强度之间的本构关系，对前人研究结果进行了优化与拓展。总体上，冰波形成及发展与水流强度有关，冰波波高与背流面波长均是水流强度的函数；盖移质输冰率不仅与水流强度相关，来冰量、相对高度均是其影响因素，建立的输冰率公式考虑了冰盖层，进一步提升了输冰率计算结果的准确性；输冰能力与水流强度呈复杂的函数关系，但水流强度仍是表征输冰能力的最佳指标之一。研究结果对冰塞形成演变及凌灾预防具有一定的理论与实际意义，但仍需通过大量的试验进行验证。

研究假定床面为定床，而天然河道均是动床，沙波的形成及演变（床面起伏）会对公式的准确度带来一定影响；另外，冰波在实际中处于动态变化，因此，输冰率理应是一个变动值，其调整过程受水流及来冰条件控制，如何量化这种调整过程需要进一步分析研究。