变截面方形桥墩折冲效果数值模拟

2022-04-27闫杰超贾恩实

水利水运工程学报 2022年2期

闫杰超，陈靖，徐华，贾恩实，陆杨

(1.中铁大桥勘测设计院集团有限公司,湖北武汉 430050；2.南京水利科学研究院,江苏南京 210029)

桥墩的局部冲刷问题历来是国内外研究关注的热点。通常解决桥墩局部冲刷的防护手段主要有实体防护与折速减冲两种[1]。前者主要包括抛石防护、扩大桥墩基础防护、混凝土模袋、混凝土铰链排防护及四脚混凝土块防护等；后者主要包括护圈防护、桥墩开缝防护、墩前排桩防护及淹没槛防护等[2]。桥墩局部冲刷防护手段多种多样，而桥墩局部冲刷防护手段的选择应“因桥制宜”，不适合的防护手段可能带来防护失效、后期维护成本高甚至影响结构安全[3]。

随着桥梁跨度的不断加大，为满足基础受力的要求，目前桥墩基础的尺寸已达到百米量级，对水流结构及局部冲刷的影响与小尺度基础差别较大，防护或维护成本也将大大增加[4-6]。目前，对于大尺度桥墩基础的冲刷防护，仍以抛石防护为主。据统计，海上风力发电机组基础的冲刷防护造价要占涡轮设计及安装总费用的30%以上[7]。苏通大桥桥墩冲刷防护工程总投资达到1.2 亿，约占总建设投资的1.86%，并仍需在防护完成后根据每年监测情况对其进行必要的补抛。可见，对于大尺度桥墩基础的局部冲刷防护问题，被动的抛石防护措施成本是巨大的。常泰过江通道主墩基础提出了台阶式沉井结构，主要利用四周伸出的一定宽度台阶消杀墩前下潜水流的方式以减小局部冲刷深度[8,9]。该种防护设计借鉴了扩大基础概念，但其基础埋深有别于扩大基础，仍属于深基基础。蒋焕章[10]通过物理模型研究了方形桥墩四周设置伸出台阶宽度对局部冲刷的影响。研究表明：墩前伸出宽度对冲刷有折减作用，但墩两侧伸出宽度对局部冲刷有不利影响。通常台阶式或类似扩大基础桥墩结构截面放置于一般冲刷线附近，则其局部冲刷将经历上部基础作用、上部与下部基础联合作用及下部基础作用3 个过程[11]。Breusers 等[12]认为若河道变化剧烈，一旦扩大部分冲刷出露，类似扩大基础结构形式将可能对防护起到反作用，实际应用时应谨慎。王迪荣[13]通过分析前苏联变截面桥墩局部冲刷研究成果发现：在桥墩墩前伸出台阶上设置倾斜坡度可避免其由于冲刷出露带来的负面影响，且具有较好的折冲效果。可见，桥墩结构的变化对其局部冲刷深度有一定影响。

目前，对利用改变或优化桥墩基础的结构形式来达到折冲的相关研究较少，但从上述变截面桥墩及扩大基础折冲研究可知，桥墩结构截面形式的改变或优化对局部冲刷的影响值得更深入探讨与研究。因此，本文以较常见的方形桥墩作为研究对象，通过墩前伸出不同宽度台阶或在台阶上设置倾斜坡度的结构改变，采用建立的桥墩局部冲刷三维数学模型，研究方形桥墩截面改变或优化对其局部冲刷的影响与折冲效果，其研究成果可对相关桥墩基础折冲影响的结构优化提供技术与理论支撑。

1 模型建立

1.1 模型概化

以文献[14]中方形桥墩为研究对象，其尺寸为a×b=0.1651m×0.1651m（长×宽）。为分析方形桥墩截面改变或优化对局部冲刷的影响特性，对方墩进行了6 组结构截面改变或优化，分为墩前伸出不同宽度台阶结构与在相应台阶上设置倾斜坡度结构两类。其中，墩前伸出不同宽度台阶结构指分别在墩前伸出台阶宽度L为b/3、2b/3与1.0b。限于研究内容及篇幅，根据文献[13]研究成果，其斜坡高度设置在接近床面以上0.4h（h为水深）处折冲效果最佳。因此，本文在墩前伸出b/3、2b/3与1.0b宽度台阶上分别设置高度P为0.4h的倾斜坡度（台阶均放置于床面位置），具体结构形式见图1。

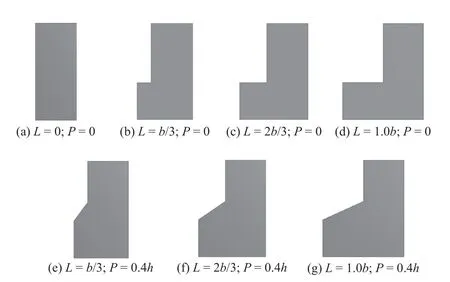
图1 变截面方形桥墩模型示意Fig.1 Sketch of variable section square pier model

通过流体计算软件建立的三维水沙数值模型对墩前伸出不同宽度台阶结构与在相应台阶上设置倾斜坡度结构的冲刷特性及折冲影响展开研究。其中，数值水槽总长4.75 m，即墩前长2.50 m，墩后长2.25 m；水槽宽1.21 m，高0.24 m。模型计算水动力条件为h=0.186 m，V=0.25 m/s。泥沙条件为中值粒径d50=0.85 mm，密度 ρ=2 650 kg/m3及休止角θ=33°。具体模拟工况及条件如表1 所示（仅列举水动力及结构尺寸条件）。

表1 模拟工况设置Tab.1 Setting of simulated working conditions

1.2 控制方程

三维水沙动力模型中水动力模型基本控制方程包括连续性方程与动量方程，湍流模型的封闭采用RNGk-ε湍流模型，自由液面的模拟采用VOF 进行捕捉。数值模拟中对于固体边界的描述应用了FAVOR 技术，这种方法计算开放体积分数和开放面积分数来定义每个单元中的障碍物，并提供了一种简单而准确的方法来表示复杂的表面，而不需要一个精细的贴体网格[15]。根据文献[16]，本文采用基本网格尺度Δl为0.012 5 m，其x、y与z方向网格节点分别为380×97×28，网格数共1 032 080个。

对于泥沙冲淤模拟，河床泥沙的形态变化受泥沙质量守恒或Exner 方程控制。泥沙模型可以同时考虑泥沙推移与悬移运动。其中，推移质输沙量采用Nielsen 控制方程[17]：

式中：Φ 为无量纲推移质输沙率；βNie为经验系数，取值为12.0；cb为床沙体积数；θ为水流无量纲希尔兹数；为泥沙无量纲临界希尔兹数。

悬移质输沙量控制方程[16]为：

式中：C为悬沙浓度；us为悬移泥沙速度；ε为扩散系数。

根据文献[18]推荐的方程计算泥沙无量纲临界希尔兹数，得其。同时，本文研究工况为来流流速V＝0.25 m/s 和水深h＝0.186 m，则根据文献[19]计算方法，计算得θ=0.024，因此，本次桥墩局部泥沙冲淤计算模拟属于清水冲刷情况。

1.3 模型验证

本文数值模型主要采用文献[14]中的数据，物理模型水槽长10 m，宽1.21 m，高0.45 m，边长为0.165 1 m 的方墩垂直插于水槽床面，布置于水槽进口下游4.0 m 处，且床面铺设0.2 m 厚均匀泥沙，泥沙中值粒径d50为0.85 mm，密度 ρ为2 650 kg/m³。同时，相应的水深为0.139 m，流速为0.22 m/s。物理模型试验在清水冲刷条件下每次试验开始时记录初始的床面高度，允许水流随时间演化，直至达到平衡冲刷深度。在每个桥墩内安装高清数码相机，观察冲刷的时间演变，确定最终的平衡冲刷深度。同时，数值模拟根据物理模型实际情况进行相应设置，模型长4.75 m，其中墩前长2.5 m，墩后2.25 m，模型高0.39 m，泥沙厚度为0.15 m。模拟采用时间步长0.2 s，总模拟时间为7 200 s。

由图2 可见，从墩前冲刷范围等深线来看，冲刷主要出现在墩前及墩侧区域，数值模拟结果与物理试验结果基本一致，墩前数值模拟冲刷范围略大于试验冲刷范围；墩后淤积区域存在一定差异，数值模拟结果的淤积范围及淤积高度偏大，这种差异通常与采用的RNGk-ε湍流模型有关，因模型不能很好地模拟墩后马蹄涡系。同时，由图3 可见，方形桥墩平面局部冲刷最大深度为0.09 m，而物理试验实测局部冲刷最大深度为0.076 m，冲刷深度误差约为15.6%，误差在可接受范围内，且数值模型能够相对较好地模拟冲刷时间演变过程，验证整体良好，说明建立的三维水沙数学模型可用于进一步的模拟研究。

图3 方形桥墩局部冲淤深度实测结果与数值模拟对比Fig.3 Comparison between the experimental results and numerical simulation of local erosion and deposition depth of square piers

2 变截面方形桥墩局部冲刷特性与折冲效果分析

2.1 变截面方形桥墩局部冲刷特性分析

由图4 可见，方形桥墩局部冲刷作为本文的对照研究工况（run1），其局部冲刷基本呈现前冲后淤的分布特性，与圆形桥墩不同处在于最大冲刷深度位于墩前钝角处，最大冲刷深度达到0.144 m，主要原因是来流水流受墩前钝角作用，床面附近泥沙受到马蹄涡涡系与加速水流作用，造成该处冲刷深度较大。

图4 方形桥墩局部平面冲淤变化分布（run1）Fig.4 Variation distribution in plane of local erosion and deposition of square piers (run1)

通过与无台阶方形桥墩局部冲刷对比可知，方形桥墩墩前设置一定伸出宽度台阶将对其局部冲刷深度起到折冲效果(图5)。对不同伸出宽度台阶的模型试验研究表明，只有台阶的伸出宽度大于或等于b/3时，台阶的影响才应该予以考虑[9]。因此，当墩前台阶伸出宽度为b/3时，其折冲效果十分有限；当墩前台阶伸出宽度从b/3增加至2b/3与1.0b时，局部冲刷深度明显减小，这与墩前台阶宽度足够消杀下潜水流及形成的马蹄漩涡有关。桥墩局部冲刷由墩前马蹄漩涡引起，研究发现其马蹄涡系影响范围通常在墩前(0.13～0.60)b内[20]，而马蹄主涡一般在墩前0.17b位置（主要受墩径雷诺数影响），对局部冲刷起主要作用[21-22]。同时，研究发现当墩前台阶伸出宽度从2b/3增加至1.0b时，出现了冲刷深度增大的现象。

图5 不同伸出宽度台阶方形桥墩局部冲刷深度变化Fig.5 Local scour depth changes of stepped square piers with different protruding widths

由不同伸出宽度台阶方形桥墩局部冲淤变化分布（图6）可知，当墩前伸出台阶宽度为b/3时，相较于无伸出台阶情况（图4），其冲刷深度最大值分布在除墩后的墩周，且墩周局部冲刷范围也相应增大，说明伸出台阶部分在其出露床面后对墩周水流结构产生了一定负面影响，增大了冲刷范围；而当墩前台阶伸出宽度从b/3增加至2b/3与1.0b时，局部冲刷深度最大值位置从上游钝角位置移至下游钝角位置，尤其当墩前台阶伸出宽度为1.0b时（图6（c）），局部冲刷深度最大值移至桥墩下游一定位置，初步分析认为该处发生了溯源冲刷，这也是为何当墩前台阶伸出宽度从2b/3增加至1.0b时，出现了冲刷深度反而增大现象的主要原因。

图6 不同伸出宽度台阶方形桥墩局部冲淤变化分布Fig.6 Variation distribution of local erosion and deposition of stepped square piers with different protruding widths

为研究墩前伸出一定宽度斜坡台阶对方形桥墩局部冲刷的影响，分别在方形桥墩墩前设置了伸出宽度为b/3斜坡台阶（run5）、2b/3斜坡台阶（run6）与1.0b斜坡台阶（run7）台阶，且斜坡高度为0.4h，并与无台阶方墩（run1）作对比分析。由图7可见，方形桥墩墩前设置一定伸出宽度斜坡台阶将对其局部冲刷深度起到折冲效果，且局部冲刷深度随着伸出的斜坡台阶宽度增加而减小。

图7 不同伸出宽度斜坡台阶方形桥墩局部冲刷深度变化Fig.7 Local scour depth changes of square piers with slope steps with different protruding widths

不同伸出宽度斜坡台阶方形桥墩局部冲淤变化分布（图8）可知，当墩前伸出斜坡台阶宽度为b/3时，相较于无伸出台阶情况（图4），其冲刷深度最大值逐渐趋于墩后，且墩周局部冲刷范围也相应增大，说明伸出台阶部分在其出露床面后对墩周水流结构产生了一定负面影响，增大了冲刷范围，但相较于无斜坡情况具有较好的折冲效果；当墩前斜坡台阶伸出宽度从b/3增加至2b/3时，局部冲刷深度减小，且局部冲刷深度最大值位置相对均匀分布在墩周，这与无斜坡情况不同；当墩前斜坡台阶伸出宽度从2b/3增加至1.0b时，局部冲刷深度进一步减小，但局部冲刷深度最大值位置移至下游桥墩钝角处，冲刷深度相较于无斜坡情况明显变小。

图8 不同伸出宽度斜坡台阶方形桥墩局部冲淤变化分布Fig.8 Variation distribution of local erosion and deposition around square piers with slope steps with different protrusion widths

2.2 变截面方形桥墩折冲效果分析

2.2.1 墩前台阶方形桥墩折冲效果分析通过上述不同伸出宽度台阶方形桥墩局部冲刷特性研究分析可知，伸出台阶宽度对折减其局部冲刷深度具有一定作用，其折冲率在台阶伸出宽度为2b/3时达到最优值，折冲率达到23%（图9）。需要注意的是虽然墩前设置伸出一定宽度台阶具有折冲作用，但对伸出宽度具有较高要求，设置伸出宽度较窄或较宽均不能达到预期折冲效果，且在墩后引起的溯源冲刷将可能造成其受力不均而发生失稳可能。

图9 不同伸出宽度台阶方形桥墩折冲率Fig.9 Reduction ratio of square piers with different protruding widths

2.2.2 墩前台阶斜坡方形桥墩折冲效果分析通过上述不同伸出宽度斜坡台阶方形桥墩局部冲刷特性研究分析可知，伸出一定宽度斜坡台阶对折减局部冲刷深度具有一定作用，折冲率在台阶伸出宽度为1.0b时达到最优值，折冲率达到38%（图10）。其具有比无斜坡台阶方形桥墩更加明显折冲效果，同时也需要注意在达到最优折冲率时，局部冲刷深度最大值出现在桥墩下游钝角处。因此，该结构形式在实际应用中应综合考虑。