基于壁面压力反馈的圆柱绕流减阻智能控制*

2022-04-27陈蒋力陈少强任峰胡海豹

物理学报 2022年8期

陈蒋力陈少强任峰† 胡海豹‡

1) (西北工业大学航海学院,西安 710072)

2) (中国船舶重工集团公司第七〇五研究所,西安 710077)

针对经典圆柱绕流问题,采用深度强化学习方法,提出了基于壁面压力反馈的圆柱绕流减阻闭环主动控制方法,并比较分析了施加控制前后圆柱阻力系数、升力系数及流场的差异.控制系统中,以圆柱壁面上均匀分布的压力探针测得的信号作为反馈,利用多层感知机建立压强信号与吹/吸射流及控制效果的映射关系,即控制策略;通过在圆柱上下表面狭缝施加连续可调的吹/吸射流来进行主动控制.同时,利用深度强化学习中的近端策略优化方法,在大量的学习过程中对该控制策略进行不断调整和优化,以实现稳定减阻效果.在圆柱绕流流动环境搭建方面,采用格子Boltzmann 方法建立与深度强化学习模型之间的交互式框架,模拟提取非定常流场条件下圆柱表面的压强信号,并计算实时调整吹/吸射流强度时圆柱表面升力、阻力数据,以评估所选控制策略的优劣.研究表明:雷诺数为100 时,主动控制策略能减少约4.2%的圆柱阻力,同时减少约49%升力幅度;同时施加主动控制后圆柱的减阻效果与圆柱回流区长度呈现强相关趋势.此外,不同雷诺数下智能体习得的策略减阻效果不同,雷诺数为200 和400 时,该主动控制策略能依次减小圆柱阻力17.3%和31.6%.本研究可为后续开展基于壁面压力反馈的圆柱流动主动控制实验以及其他复杂环境下钝体流动智能控制提供参考.

1 引言

流动控制根据是否需要外部能量输入分为被动流动控制和主动流动控制[1].被动控制具有无需能量输入、设置简单、成本低等优点,但当流场实际情况偏离预期时,控制往往难以达到最佳效果[2].在主动控制中,根据是否需要从流场中获取反馈信息并用以调节激励器的输出大小,可以分为开环控制和闭环控制[3].研究发现,闭环主动控制相较于开环控制具有自适应能力强的特点,能够充分发挥激励器的潜力,在少量能量输入情况下往往就能得到很好的控制效果,因而有着更大的潜力[4].然而,非线性的Navier-Stokes 方程所描述的流场具有高维、多模态等复杂特征,导致设计有效的实时闭环主动流动控制策略往往十分困难[5].

近年来,迅速发展的深度强化学习(DRL)以其擅长与环境进行交互的特点,为上述流动控制难题带来了新的思路.研究表明,深度强化学习能够在高维、非线性等复杂环境中有效地习得控制策略[6].如果利用深度强化学习与流动控制环境进行交互,在不断试错、调整优化策略后,由习得策略建立控制律,对于闭环流动控制方法来说具有重要意义.Rabault 等[7]将深度强化学习应用于钝体减阻,利用近端策略优化方法[8]成功习得了能够实现稳定减阻约8%的闭环主动控制策略.该研究中,将位于圆柱周围和下游流场中的151 个传感器(每个传感器同时采集流向速度及横向速度)测得的速度作为反馈信号,并将奖励函数(与升力系数和阻力系数有关)作为奖惩机制.Paris 等[9]引入一种新算法(S-PPO-CMA)优化传感器位置,在雷诺数120 时,成功习得了稳定减阻约18.4%的闭环主动控制策略.任峰等[10]基于格子Boltzmann 方法搭建流动环境,在弱湍流条件下成功习得减阻的闭环主动控制策略,实现了约30%的圆柱减阻效果,为优化传感器布局,进行了敏感性分析.

上述研究均以尾流中的速度传感器等作为反馈信号.考虑到应用条件下的实际情形,在尾流固定位置处布置传感器技术实现上比较困难,因此本研究以实际应用场景中较容易测得的壁面压力作为反馈信号.本文采用GPU 加速的格子Boltzmann方法[11]对低雷诺数下的圆柱绕流进行数值模拟,将深度强化学习应用于主动流动控制,并通过分析施加控制前后射流速度的变化得到主动控制对流动的影响机制.

2 数值模拟环境和智能流动控制方法

2.1 物理模型

本文选取了图1 所示的物理模型.其中,直径为D的圆柱放置在长L=21.79D,宽H=4.06D的狭窄管道中.将圆柱中心设置为坐标系零点,与入口边界距离L1=2D,与出口边界距离L2=19.79D.为了促进涡旋脱落,圆柱中心略微偏离计算域中心线(y方向上向上偏离0.05D).由于计算域较为狭窄,上下两侧壁面会对圆柱的升阻力系数有所影响,但不影响最终控制效果.雷诺数定义为Re=UmD/υ,其中D为圆柱直径,υ是流体的运动黏度,Um为入口处的平均速度.参考时间T定义为T=D/Um.

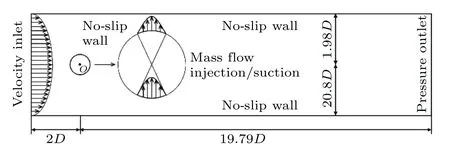
图1 物理模型示意图Fig.1.Schematics of the physical model.

本文圆柱的阻力系数和升力系数分别用CD和CL表示,定义如下:

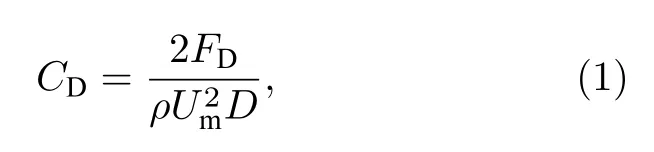
其中ρ为流场中流体的密度,FD以及FL分别为圆柱所受的总阻力和总升力.

本文通过圆柱上下表面的狭缝施加吹/吸射流控制,狭缝宽度与圆心角为10°的弧长相对应,为保证零质量流量射流,上下表面射流速度的大小与方向均相同.为了保证控制的连续性,并避免施加控制后射流速度的跳跃,将射流速度表示为

其中Ujet与分别为当前时间步以及下个时间步的射流速度,两个时间步的时间间隔为T/δt=800 (δt=1 为格子时间),at指在当前时间步下,深度强化学习智能体输出的动作值(智能体及动作值的详细解释在2.4 节给出).α为数值参数,α=0.1 与Rabault 等[12]一致.(3)式为指数衰减形,其表达形式及α的取值会影响训练效率,详见参考文献[12].

本文奖励函数设置为

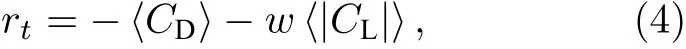
其中〈·〉代表在两次施加激励过程中进行时间平均,w为权重,本文将权重设置为1,这样不仅能减少圆柱阻力,还能保证在较低雷诺数时圆柱升力系数不会出现显著零偏,详见参考文献[10].

2.2 数值模拟方法

由于格子Boltzmann 方法不依赖连续介质假设,算法简单,具有良好的计算局部性等优点[13,14].本文基于格子Boltzmann 方法建立流动数值模拟环境.本文的格子Boltzmann 求解器使用了D2Q9格式[15](二维流动,每个格点处速度向9 个方向离散)作为离散速度模型,通过多松弛时间算法[16,17]来提高数值模拟的精度和稳定性,采用He-Luo 模型[18]确保本文中流体的不可压缩性.

本文中多松弛时间模型表达式为

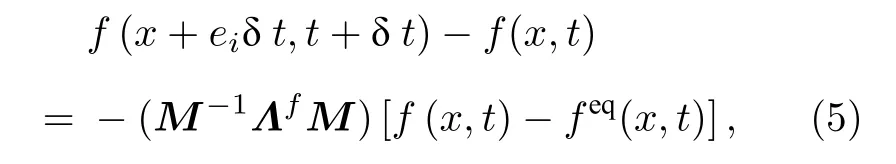
式中f(x,t)指在t时刻x位置处的分布函数,feq为平衡态分布函数,ei为粒子的离散速度,δt为格子时间步长,M称为变换矩阵,可以将速度空间转换至矩空间.松弛参数设置为

其中τ为松弛时间,松弛时间与运动黏度关系为τ=0.5 +,cs=3–1/2为格子声速.

边界条件的设置与此前工作[10]类似,入口处的速度设置为抛物线形,数学表达式为

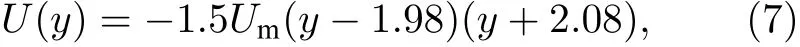
出口处的压力设置为零,入口和出口均采用非平衡外推格式[19].上下壁面采用具有二阶精度的半步长反弹格式[20],圆柱曲面使用双线性插值法进行处理[21],上下壁面及圆柱表面均为无滑移壁面.此外,圆柱受力采用改进的动量交换方法求得[22].

2.3 数值模拟验证

网格数量以及时间分辨率的选取,对数值模拟时的计算精度和计算耗时有一定的影响,表1 测试了Re=100 时三种不同网格数和时间分辨率下的算例,对比了这些算例中圆柱的各个参数.其中T为参考时间,Sr为斯特劳哈尔数(Sr=f D/Um,其中f为涡旋脱落频率).

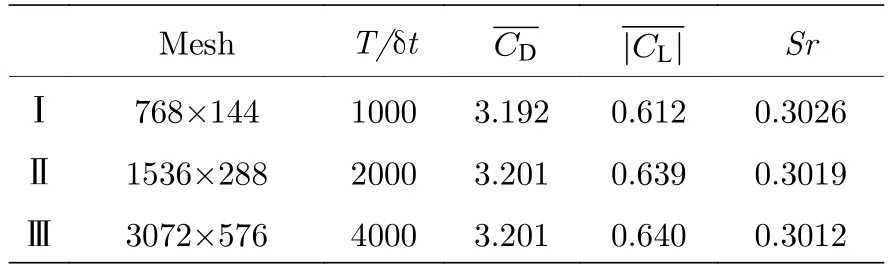
表1 无关性验证(Re=100)Table 1.Validation and convergence study (Re=100).

从表1 中可以看到,与算例Ⅲ(本文最佳的网格数及时间分辨率)相比,算例Ⅰ中平均阻力系数与平均升力系数的绝对值分别相差0.009 和0.028,相对误差分别为0.3%和4.4%.而算例Ⅱ的平均升力系数的绝对值相对误差在0.5%以内,且计算耗时小于算例Ⅲ,很好地满足了低计算耗时和高计算精度的要求.因此,Re=100 时,本文以表1 中的算例Ⅱ为标准,搭建流动数值模拟环境.

在合适的时间分辨率和网格数下,成功搭建了Re=100 时的流动数值模拟环境.表2 给出了该环境下的计算结果以及其他学者数值模拟的结果,包括圆柱表面的最大阻力系数、最大升力系数以及涡旋脱落频率(Sr).对比发现,各个计算结果相对偏差均在2.5%以内,这验证了格子Boltzmann 方法在该问题上的准确性与可靠性.

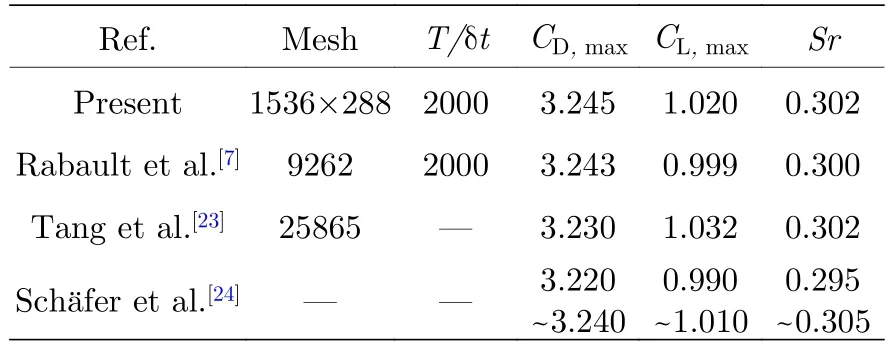
表2 Re=100 时最大升阻力系数CD,max,CL,max 与Sr 对比Table 2.Comparison of CD,max,CL,max and Sr at Re=100.

2.4 智能流动控制方法

深度强化学习的本质是互动学习[25].智能体(本文指模拟人的思维决策过程,可以同环境相交互的程序)主要通过以下三个方面与环境进行交互:动作at,状态st和奖励函数rt.本文所使用的是深度强化学习中的近端策略优化方法(PPO),具有较高的稳定性和可靠性等优点[8].

首先引入轨迹τt的概念,表示在给定参数θ下,某次学习时,状态-动作-奖励函数随时间的变化关系:

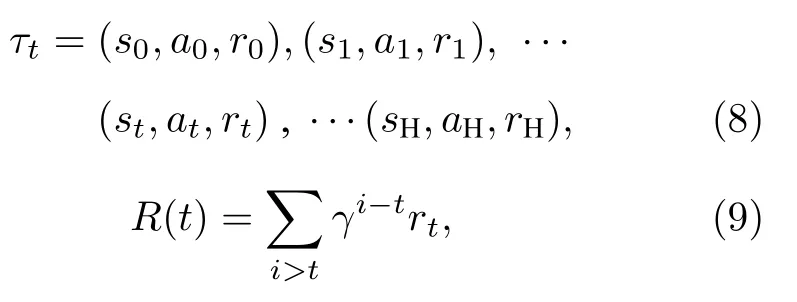
(8)式指环境输出状态值s0给DRL 智能体,选择动作a0,并得到奖励函数r0,环境被动作改变,输出新的状态s1.经过不断重复,得到某次学习下的控制策略,并以累计奖励函数R(t)评估策略,其中γ(0 <γ<1)为折扣系数,本研究中固定为0.97.

近端策略优化方法使用了两组人工神经网络,分别为动作策略(输入状态,输出动作的概率分布)的actor 网络和评价策略(输入状态,得到值函数,计算出优势函数)的critic 网络,即actor-critic网络.创建critic 网络用以减小实际奖励与预期奖励的数学期望之间的差异,即

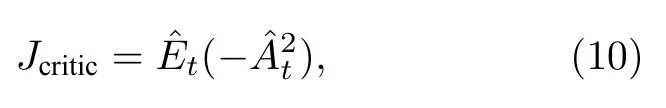
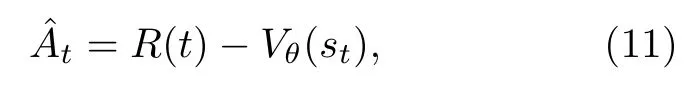
其中参数θ代表神经网络的所有权重的集合,V(st)指值函数,即状态st下所有可能的动作与其累计奖励函数的乘积的和(预期奖励的数学期望).

本文依据Schulman 等[8]的工作,选取了近端优化策略中actor 网络的目标函数,用于输出某状态下动作的概率分布.该目标函数算法简单且具有良好的稳定性[8].其数学表达形式为:

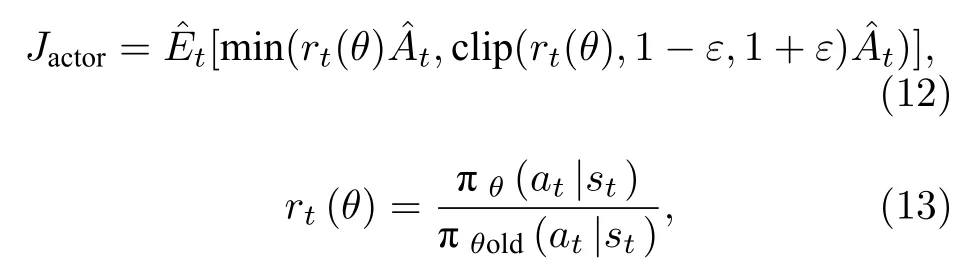
其中,rt(θ)指的是新旧策略概率比(πθ(at|st) 和πθold(at|st)分别为当前策略和旧策略在状态st下采取动作at的概率).clip 函数用于限制新旧策略概率比,是指将rt(θ)的大小限制在[1–ε,1+ε]之间,当rt(θ)的值大于1+ε时,用1+ε代替rt(θ),当rt(θ)小于1–ε,用1–ε代替rt(θ).ε是超参数,设置为0.2,与Schulman 等一致,在Schulman 文中,与ε=0.1 和ε=0.3 相比,ε=0.2 时算法的效果最佳,详见参考文献[8].min()即取下界,具体理解为:当>0 时,当前动作产生的奖励估计大于预期奖励的数学期望,因此增加新策略中当前动作出现的概率,为提高训练的稳定性,限制其不能超过原策略的1+ε倍;反之,当<0 时,限制其不能小于原策略的1–ε倍.

2.5 智能流动控制方法验证

本节主要复现了Rabault 等[7]的结果,并采用了相同位置的速度传感器.Re=100 时,智能体以流场速度作为反馈信号,训练得到减阻的闭环主动控制策略.由于已有学者[7,10,12]开展过相似的研究内容,此处不再详细描述.

图2 给出了基于速度反馈的智能体的训练过程,本文进行三次不同的训练,并对三次训练过程中的阻力系数取平均值,得到一条更为平滑的曲线.每一训练集(episode)均相当于一次完整的数值模拟过程,持续时间为32T,可以看到,随着训练集数的增加,在200 集后,阻力系数(通过对每一集后半段的阻力系数取平均得到对应阻力系数)逐渐稳定,在400 集时阻力系数大约在2.98 附近,但仍然有大幅度波动出现,这是由于深度强化学习智能体的训练过程具有一定的随机性.

图2 智能体训练过程(速度反馈)Fig.2.Learning curves of DRL agent (velocity feedback).

图3 为训练完成,智能体已习得闭环主动控制策略后,施加控制前后圆柱的阻力系数随时间变化对比图,可以看到,施加控制至流场达到稳定后,圆柱的阻力系数为2.989,减阻率为6.6%,且射流速度仅为入口处平均来流速度的0.15 倍.

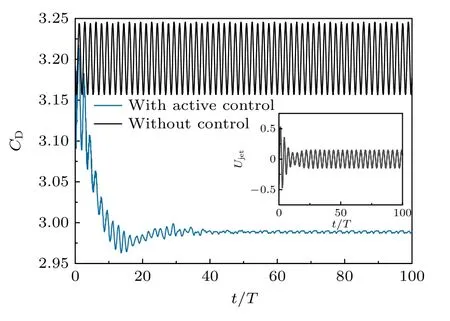
图3 控制前后阻力系数(CD)随时间变化图Fig.3.Temporal variations of drag coefficient (CD) with and without active flow control.

3 基于壁面压力反馈的智能流动控制

3.1 未控制下压力曲线

在成功搭建流动控制环境后,智能体需要基于有限的流场信息来训练主动流动控制策略.考虑到速度传感器成本大,在尾流处布置困难,难以用于实际实验中.而压力传感器较速度传感器成本低,在圆柱表面处布置容易.本节通过壁面压力反馈方法代替原来的尾流速度反馈方法.

考虑到压力探针数量对智能体的影响,本文分别对比了6,14 和30 个压力探针下智能体习得控制策略的减阻效果.图4 分别给出了6,14 及30 个压力探针的位置分布,采用在壁面上均匀分布的方式并避开了圆柱上下表面的吹/吸射流.

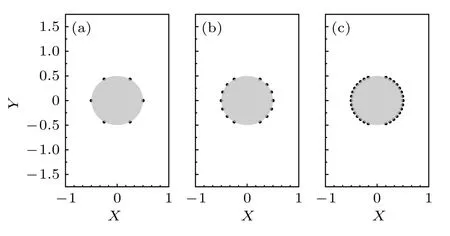
图4 压力探针位置图 (a) 6 个压力探针;(b) 14 个压力探针;(c) 30 个压力探针Fig.4.Schematics of the pressure sensors position:(a) 6 pressure sensors;(b) 14 pressure sensors;(c) 30 pressure sensors.

本文圆柱曲面边界处理方法为双线性插值法[21],由于圆柱表面位于流体格点与固体格点之间,无法直接得到压力分布曲线.因此采用了多次线性插值的方法,通过圆柱表面附近格点间接得到未控制下圆柱的压力分布曲线.

为了和Tiwari 等[26]进行对比,本节搭建了Re=20 时的数值模拟环境,并得到圆柱表面的压力分布曲线.其中,压力经过无量纲处理,即

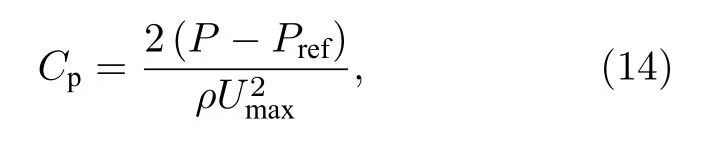
式中,Pref为参考压力,这里Pref=1907,Umax=1.5Um是入口处的最大速度.

Re=20 时圆柱表面压力分布曲线对比图如图5 所示,其中点(0.5,0)作为横坐标起点,逆时针方向为正方向.可以看到本文得到的Re=20时的圆柱压力分布曲线与Tiwari 等[26]的结果几乎重合.

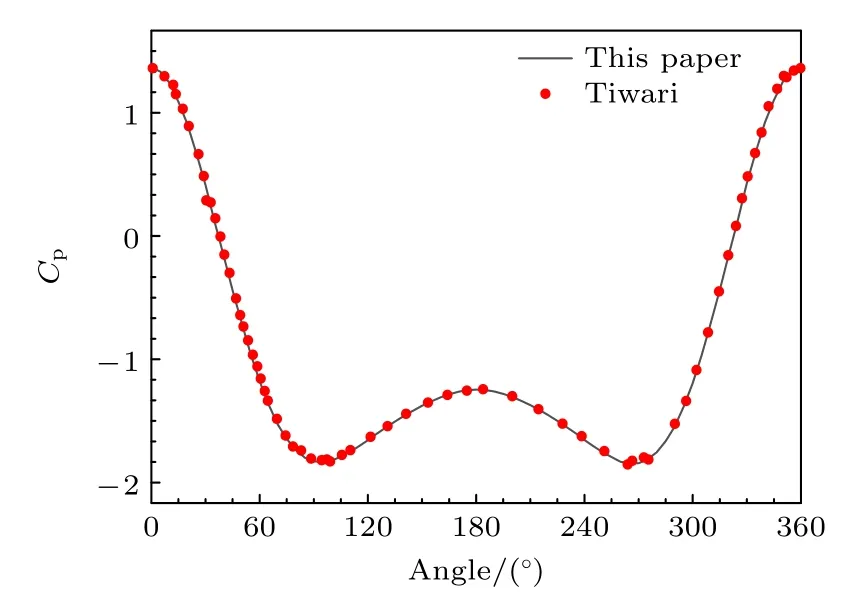
图5 圆柱压力分布曲线,Re=20Fig.5.Pressure distribution curve along the cylinder surface,Re=20.

3.2 控制策略学习过程

Protas 和Wesfreid[27]将圆柱的阻力分为两部分,一部分为由涡旋脱落引起的阻力,另一部分为圆柱无涡旋脱落时的阻力.研究表明,对于圆柱绕流而言,主动控制仅能减少由涡旋脱落引起的阻力[27−29].同时,圆柱阻力与回流区长度具有一定的联系,在无涡旋脱落时圆柱尾流处回流区呈细长状,长度随着Re的提高而增加.施加主动控制后,圆柱阻力减小,此时回流区长度更接近稳定无涡旋脱落时的回流区长度.Rabault 等[7]指出,Re=100 时,本文计算域下无涡旋脱落时圆柱的阻力系数约为2.93.

本节智能体以壁面压力作为反馈信号,并进行训练,训练曲线如图6 所示.与图2 相比,图6 中的智能体需要更多集数进行训练以使阻力系数趋于稳定.训练完成后,将训练过程中阻力系数最小时对应的控制策略作为本次训练得到的最佳策略.智能体分别采用6,14 和30 个压力探针作为反馈信号,通过主动控制和无控制得到的圆柱阻力系数、升力系数和射流速度随时间变化曲线,如图7所示.

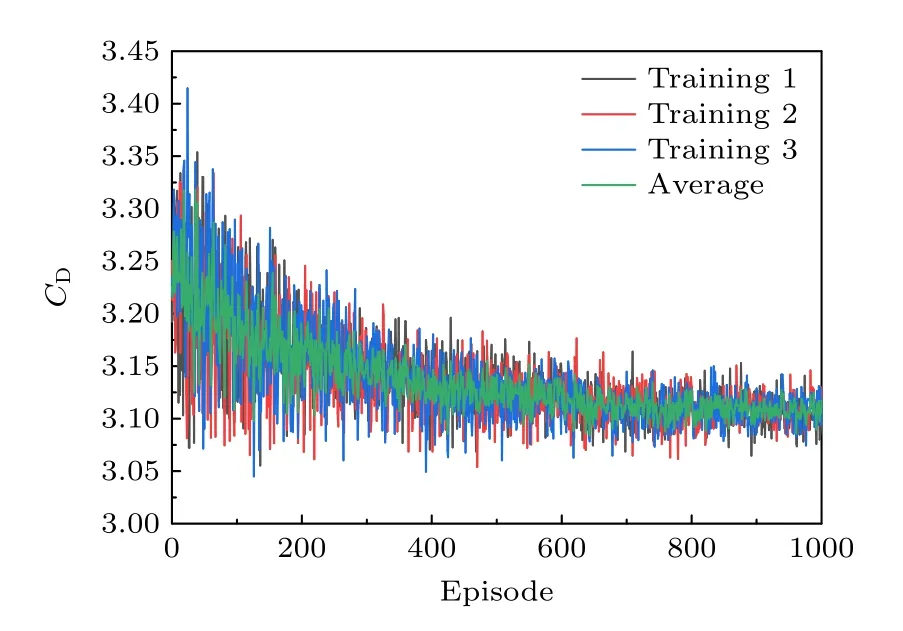
图6 智能体训练过程(压力反馈)Fig.6.Learning curves of DRL agent (wall pressure feedback).

图7 主动控制和无控制下圆柱的阻力系数(CD),升力系数(CL)和射流速度(Ujet)变化曲线,Re=100Fig.7.Temporal variations of drag coefficient (CD),lift coefficient (CL),and jet velocity (Ujet) with and without active control,Re=100.

如图7 所示,探针数量不同的智能体施加主动控制均能减少圆柱阻力.当压力探针数量为6 时,能习得减阻的闭环主动控制策略,但是仅将圆柱的平均阻力系数减少到3.11 左右,平均升力系数由–0.026 增加至–0.019,减阻效果达到了2.9%,减少的阻力占因涡旋脱落产生的阻力的34.1%.相比之下,压力探针数量增加至14 时,智能体习得的控制策略能将平均阻力系数减小到3.07 左右,平均升力系数由–0.002 减少至–0.013,减阻效果达到了4.2%,减小的阻力占由于涡旋脱落导致的阻力的51.3%.当压力探针增加至30 个时,习得的控制策略也只能将平均阻力系数减小到3.08 左右,平均升力系数由0.010 增加至0.012.同时,升阻力系数的变化幅度减少.阻力波动从无控制下的[3.16,3.25]分别减少至[3.08,3.13](对应6 个压力探针),[3.05,3.09](对应14 个压力探针),[3.06,3.09](对应30 个压力探针).升力波动从无控制下的[–0.99,1.01]分别减少至[–0.62,0.63](对应6 个压力探针),[–0.53,0.52](对应14 个压力探针),[–0.55,0.57](对应30 个压力探针).从射流速度随时间变化曲线中可以看出,主动控制时,首先以较大的射流速度改变流场结构,此时与圆柱阻力快速减少相对应.在控制达到稳定后,仅需少量能量(以14 个探针为例,约为刚开始控制时最大射流速度的0.5 倍,入口处平均速度的0.15 倍)即可以达到很好的减阻效果.

3.3 控制前后流动的变化

本节试图分析控制前后流动的变化,来探究主动控制对流场的影响.图8 为控制前后的瞬时流场云图(以14 个压力探针习得的控制策略为例),每张图的上部分为无控制下的流场云图,下部分为施加主动控制下的流场云图.由于在Re=100 时进行数值模拟,云图中可以看到规则的流场,受逆压梯度和流体黏性的影响,圆柱壁面产生边界层分离现象,并在分离点后形成回流区(流向速度为负的区域)和尾流区(圆柱尾涡周期性脱落).

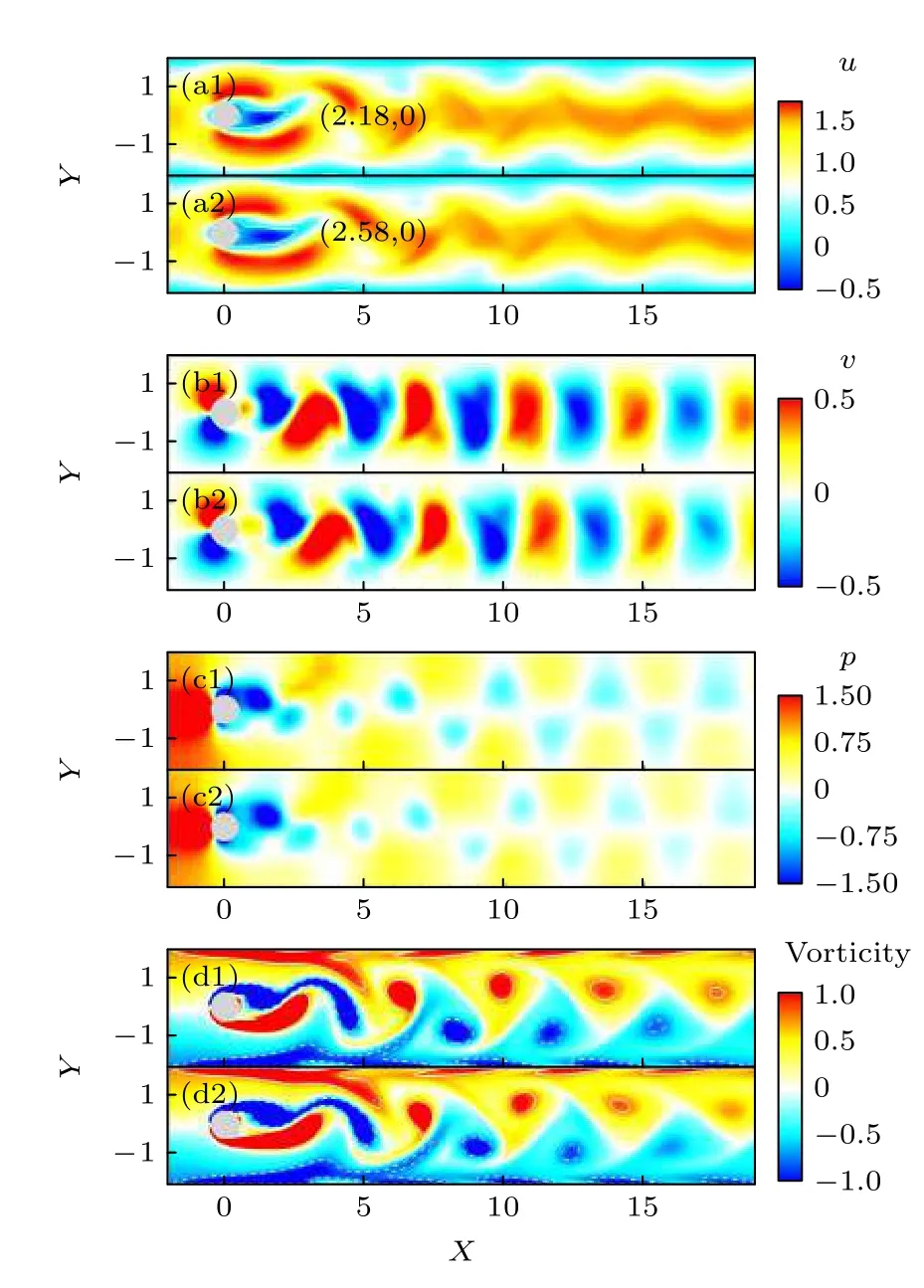
图8 Re=100 时的瞬时流场云图(a1)—(d1)无控制下流向速度,横向速度,压力及涡量云图;(a2)—(d2)主动控制下流向速度,横向速度,压力及涡量云图Fig.8.Instantaneous contours of flow fields at Re=100:(a1)–(d1) Contours of streamwise velocity,transverse velocity,pressure,and vorticity without active control;(a2)–(d2) contours of streamwise velocity,transverse velocity,pressure,and vorticity with active control.

从瞬时的流向速度对比云图中可以看到,与控制前相比,施加主动控制后圆柱上分离点位置变化较小,回流区长度显著增加,达到了2.08D左右,而控制前回流区长度仅有1.68D左右,回流区长度增加了23.8%.

从瞬时横向速度对比云图和瞬时压力对比云图中可以看到,相比无控制下的流场,主动控制下流场内流体的瞬时横向速度变小,圆柱前后的压力差(圆柱的压差阻力)减小,尾流处压力为负的区域面积增大.从瞬时涡量对比云图中可以看到,主动控制下尾流处涡的形成和脱落过程被改变,涡开始脱落的位置和未控制时相比向下游推移,同时涡脱落频率和涡量强度减小.

对500 张云图(约3 个涡脱落周期)取平均得到如图9 所示的时间平均的流向速度云图、横向速度云图和压力云图.分析流场时均云图同样看到,与无控制情况相比,施加主动控制后圆柱分离点位置变化较小,回流区长度显著增加,时均压力云图中,圆柱前后的压力差变小,尾流处压力为负的区域面积增大,这说明施加主动控制能减少圆柱的部分压差阻力.

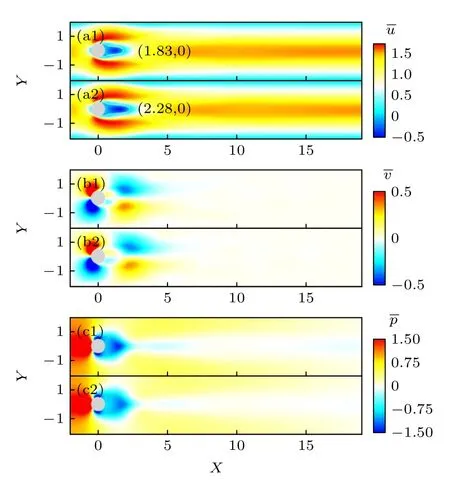
图9 Re=100 时的时均流场云图 (a1)—(c1)无控制下流向速度,横向速度及压力云图;(a2)—(c2)主动控制下流向速度,横向速度及压力云图Fig.9.Time-averaged contours of flow fields at Re=100:(a1)–(c1) Contours of streamwise velocity,spanwise velocity,pressure,and vorticity without active control;(a2)–(c2) contours of streamwise velocity,spanwise velocity,and pressure with active control.

4 不同雷诺数下的闭环主动控制策略

在第2 节中,智能体始终在Re=100 时的数值模拟环境中进行训练.随着Re的改变,绕流流场也会发生变化,研究指出当Re增加时,因涡旋脱落产生的阻力占总阻力的比例提高,且无涡旋脱落时圆柱尾流处回流区长度也随之增加[25,27−29].本节通过对比不同Re智能体习得的闭环主动控制策略(以第3 节14 个压力探针为例),探究Re对减阻效果及流场的影响.

Re=100,200 和400 时,智能体施加主动控制后得到的结果如图10 所示.图10 中的数据表明,Re不同时,智能体均能习得减阻的闭环主动控制策略,在本文研究范围内(Re=100—400),无控制下圆柱的阻力系数与升力系数的变化幅度随着Re的增大逐渐提高,主动控制下圆柱减阻率同样随着Re增大逐渐提高.当Re=100 时,主动控制下圆柱的平均阻力系数达到稳定时仅仅只有3.07,阻力系数变化幅度从未控制下的0.096 减少至主动控制下的0.054,减阻效果达到了4.2%;当Re=200 时,主动控制下圆柱的平均阻力系数达到稳定时为2.59,减阻效果达到了17.3%;Re=400 时,施加控制后圆柱的平均阻力系数最终稳定在2.15 左右,阻力系数幅值从未控制下的0.504 减少至主动控制下的0.129,减阻效果高达31.6%.不同Re下升力系数变化幅度均减少,Re=100 时,升力系数变化幅度由[–0.98,1.01]减少至[–0.53,0.52];Re=200 时,升力系数变化幅度[–2.11,2.16]由减少至[–1.09,1.22],控制下升力系数平均值为–0.025;Re=400 时,升力系数变化幅度[–2.78,2.86]由减少至[–0.73,0.33],控制下升力系数平均值为–0.212.

图10 主动控制与无控制下的圆柱阻力系数(CD),升力系数(CL)和射流速度(Ujet)变化曲线Fig.10.Time-resolved value of drag coefficient (CD),lift coefficient (CL),and jet velocity (Ujet) with and without control.

通过研究图10 中射流速度随时间变化的曲线,可以发现闭环主动控制策略的具体实施方案.如第3 节所述,施加主动控制时,智能体首先以较大的射流速度改变流场结构,随后,以较小的射流速度维持流场形态.和Re=100 时的射流速度不同,Re=400 时射流速度在达到平衡时出现显著的零偏,本文认为这是因为当Re增加后,圆柱减少了更多的阻力,使得阻力系数的绝对值在奖励函数中的占比较大,这使得升力系数可能出现较大的零偏.可以通过提高奖励函数中升力系数的权重以减少射流速度的零偏,详见参考文献[10].

Re=200 和Re=400 时控制前后的时均流向速度云图如图11 所示.可以发现,在本文的Re范围内,圆柱减阻率与圆柱回流区长度强相关,Re越高,主动控制下圆柱减阻率越大,回流区长度越长.Re=200 时,回流区长度增加136.7%;Re=400 时,回流区长度增加341.5%.

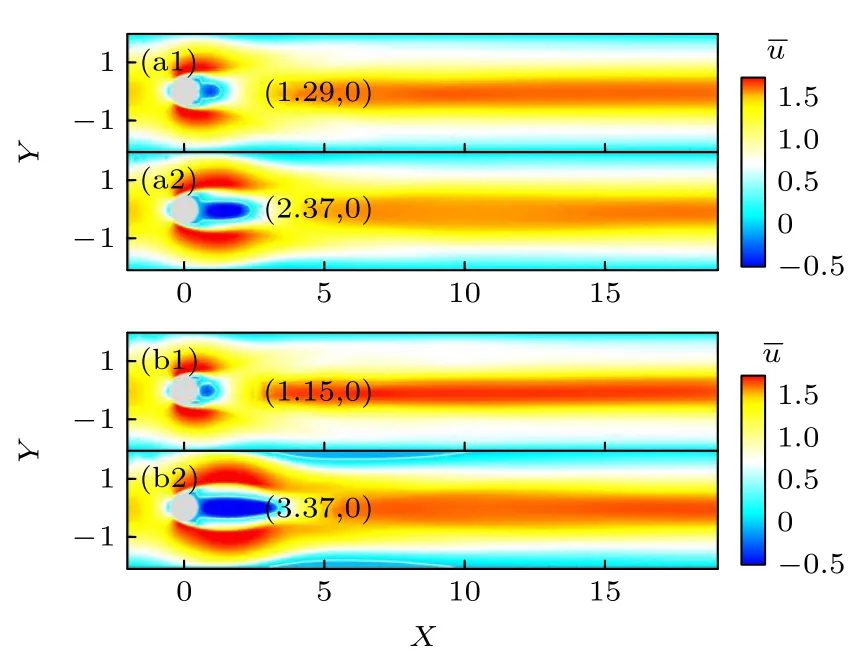
图11 无控制下和施加主动控制下的时均流向速度云图(a1) Re=200,无控制;(a2) Re=200,施加控制;(b1) Re=400,无控制;(B2) Re=400,施加控制Fig.11.Time-averaged streamwise velocity fields without control and with active control:(a1) Re=200,without control;(a2) Re=200,with control;(b1) Re=400,without control;(b2) Re=400,with control.