基于分段边缘拟合的测风多普勒差分干涉仪成像热漂移监测方法*

张亚飞 冯玉涛 傅頔 畅晨光 李娟 白清兰 胡炳樑

1) (中国科学院西安光学精密机械研究所,光谱成像技术重点实验室,西安 710119)

2) (中国科学院大学,北京 100049)

多普勒差分干涉仪是近年来发展起来的一种适用于中高层大气风场星载测量的干涉仪,它依靠对干涉图相位的精确反演计算气辉谱线的多普勒频移得到大气风速.环境温度的变化导致干涉仪光机组件发生热变形,造成成像面在干涉方向上的热漂移,改变相位的像元分布,直接引入相位误差从而影响风速反演.为了减小这种成像热漂移对多普勒差分干涉仪相位反演的影响,本文用分段拟合的方法检测光栅的标尺刻槽在干涉图中成像图案的边缘,定位刻槽图案的亚像元位置并依此监测成像热漂移.在近红外多普勒差分干涉仪样机的热稳定实验中,像面热漂移检测结果与环境温度在高频振荡变化趋势上表现出较高一致性,二者相关系数经去基线后可达0.86,而干涉图相位漂移经成像热漂移校正后其高频振荡也得到大幅抑制,证明了该算法的有效性.为了进一步验证该算法精度,计算了数据信噪比以及拟合所用各项数据分布特征参数误差对边缘检测的影响,结果表明,边缘检测精度主要受数据信噪比和条纹频率参数准确性的制约,当拟合用条纹频率参数误差小于0.5%而其他数据分布特征参数误差在1%以内,数据信噪比在约35 倍以上时,本文算法可以实现高于0.05 像元的检测精度.

1 引言

中高层大气风场信息可以为建立中间层、低热层和电离层之间的动量和能量的耦合提供参考,为中长期的天气预报提供数据支持,为军事和航天活动的顺利开展提供可靠保障[1−7].多普勒差分干涉仪是近年来发展起来的一种被动式风场干涉测量技术,与传统的基于迈克耳孙(Michelson)干涉仪和法布里-珀罗(Fabry-Perot)干涉仪的干涉测风技术相比,它具有结构简单、光通量大、装调精度要求低及具备多谱线探测能力、可以实现同步定标等优点,适合搭载于卫星平台进行中高层大气风场测量[6−8].2019 年10 月,由美国海军实验室研制的基于多普勒差分干涉技术的MIGHTI(Michelson interferometer for global high-resolution thermospheric imaging)仪器已搭载于ICON(ionospheric connection explorer)卫星成功发射并开始运行[9].

风速是风场信息中最重要的参数,多普勒差分干涉仪以大气气辉的辐射谱线为探测对象,对干涉图相位进行精确反演,通过与零风速参考之间的相位差计算气辉谱线的多普勒频移从而得到风速[10,11].多普勒差分干涉仪要达到实用的测风精度(≤10 m/s),需要测量相当于波长1/3×10–7级别的频移[7].而工作环境温度的变化会引起干涉仪光学元件和结构组件工作特性的变化,带来干涉图相位漂移、调制度降低和倾斜畸变等负面影响,影响相位测量的精度和准确性[12−14].其中结构支撑组件的热膨胀变化造成干涉仪、成像镜以及探测器之间的相对位移,这种像面的热漂移改变了干涉条纹的像元分布,如果不进行检测校正的话,会直接引入随温度变化的相位误差[9].

为了监测并校正像面热漂移带来的相位误差,Marr 等[9]在干涉仪光栅工作面刻蚀出周期刻槽图案,利用干涉图像中刻槽图案像元位置的变化检测像面热漂移,利用梳状函数、矩形窗函数以及高斯扩展核函数的卷积生成周期刻槽模拟函数,结合刻槽内外的数据分布特征生成仿真数据拟合刻槽的位置.为获得准确的像面热漂移检测结果,该方法在先行生成周期刻槽模拟函数时需要非常准确的刻槽周期、边缘坡度等参数,而获取这些参数需要对大量热稳定条件下的标定数据进行拟合并对结果平均,而且对刻槽特征的周期性要求较高.本文提出了一种逐刻槽边缘分段拟合检测干涉图像中刻槽图案亚像元位置的像面热漂移监测方法,不需要先行确定刻槽的特征参数,就可以单独检测每个刻槽边缘的亚像元位置,而且对刻槽特征的周期性要求较低.本文基于近红外多普勒差分干涉仪样机的热稳定测试数据进行像面热漂移监测,对比干涉图像中刻槽图案亚像元位置与环境温度的变化,利用刻槽漂移监测结果进行了相位校正.最后仿真数据信噪比、刻槽内外数据分布特征参数等对算法的影响,分析了算法的精度表现.

2 多普勒差分干涉仪像面热漂移监测方法

多普勒差分干涉仪基于迈克耳孙干涉原理发展而来,其两臂为以Littrow 角倾斜固定的光栅,两臂之间存在非对称偏置量△d,其基本结构如图1所示.入射光经过准直镜准直到达分束器,被分为两条光臂,两臂的光各自经过光栅的衍射作用返回分束器,在空间中相遇形成Fizeau 干涉条纹,被条纹成像镜成像于探测器[8].目前多普勒差分干涉仪进行相位反演主要用的是基于傅里叶变换(Fourier transform,FT)的反演方法,其流程如图1 所示.首先利用FT 把实条纹数据变换至频域,在频域提取特征峰得到目标谱,再对目标谱进行傅里叶逆变换得到复干涉图,最后通过反正切计算得到每个像元位置上的相位分布[8,15−17].

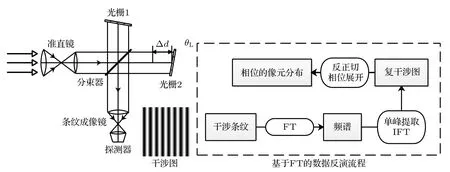
图1 多普勒差分干涉仪基本结构以及基于FT 的相位反演流程示意Fig.1.Configuration of Doppler asymmetric spatial heterodyne interferometer and phase inversion process based on Fourier transform.

2.1 像面热漂移监测原理

多普勒差分干涉仪将光栅工作面上激光刻蚀出的刻槽图案成像于干涉图像中,而刻槽图案所成像在图像中像元位置的变化就对应探测器与干涉仪之间的相对位移.刻槽外部光栅正常工作,对应图像为正常的干涉条纹,而在刻槽内部光栅的工作面被破坏,不能起到正常的衍射作用,对应图像则为亮度均匀的阴影图案,如图2 所示.对于一行含有刻槽阴影图案的干涉条纹数据来说,如果将刻槽内外区域视为两个不同的独立信号,则刻槽相当于起到了对两种信号的选择作用,这种选择作用可以表达为

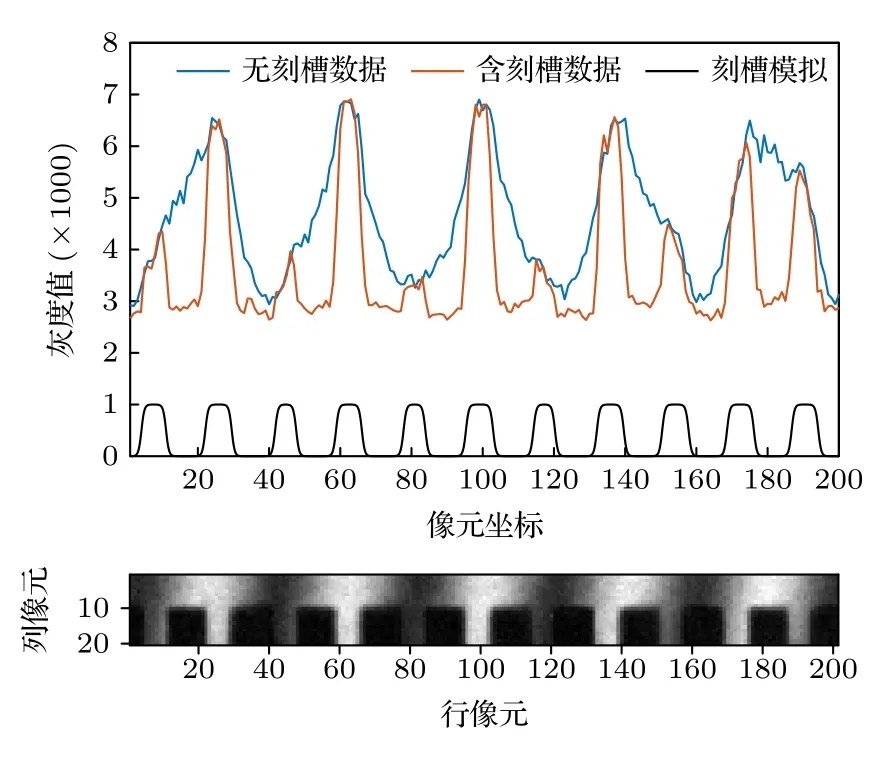
图2 从实测干涉图像中部分截取的光栅刻槽图案(下);在刻槽顶端选取的邻近两行数据,其中一行含刻槽,另一行为正常的干涉条纹(上)Fig.2.Notch pattern partly intercepted from laboratory measured interferogram (the below part);the neighboring two lines of data selected at the top of notch pattern,one is the notch row,and the other is the normal interference fringe (the upper part).

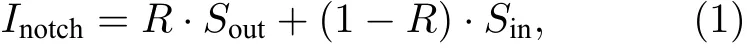
其中,Inotch为含刻槽区域的行干涉数据;Sin代表刻槽内的数据分布;Sout代表刻槽外的数据分布;函数R模拟刻槽的选择作用,在刻槽内部函数值为0,刻槽外部函数值为1,在边缘处则函数值介于0 和1 之间.

在数字图像处理领域,拟合法是经常用于亚像素边缘检测的一种方法,其基本思想是根据已知的图像边缘特性进行数学建模,用特定的函数形式生成连续曲线去拟合贴近目标边缘及附近点的离散特性,再根据拟合函数确定目标边缘的各个参数值,如位置、形状、大小等[18−20].根据(1)式,对于含刻槽数据Inotch,只要刻槽内外的数据分布Sin和Sout已知,就可以在每个边缘处,选取边缘附近的数据进行拟合以获取其亚像元位置.多普勒差分干涉仪只在光程差方向有干涉调制,因此,如果在刻槽顶端或底端取邻近两行数据,就可以近似认为含刻槽行数据中刻槽内的条纹与不含刻槽行条纹的分布特征相同,而在刻槽区域内,由于不同刻槽内均为亮度统一的均匀分布,其分布特征值容易通过统计的方法确定.于是,分段拟合得到刻槽的每个边缘的亚像元位置后,就可以以此为依据判断连续采集图像过程中像面的热漂移.

2.2 像面热漂移监测算法设计

利用拟合法进行亚像素边缘检测具有精度高、受噪声影响小的优点,但需要根据目标边缘特征选择合适的边缘模型.本文选择Sigmoid 函数作为边缘模型进行拟合.由于Sigmoid 函数只是用来模拟刻槽的选择作用而不是直接拟合边缘的灰度值,函数值介于0 和1 之间,因此所用的边缘模型为调整后的Sigmoid 函数,其表达形式可以表达为[20,21]

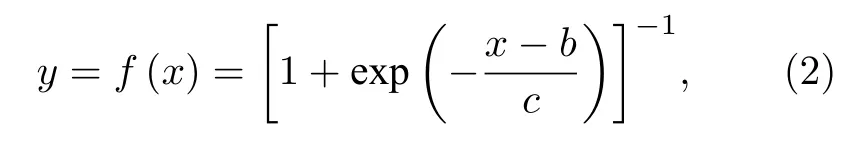
其中,b为Sigmoid 函数在x方向的偏移,表征边缘中心的位置;c表征边缘的坡度.对单幅图像中的刻槽图案进行边缘检测的算法流程可以总结如下.

步骤1在刻槽区域顶端或者底端选择邻近两行数据,一行含刻槽数据,另一行不含刻槽数据.

步骤2按照(3)式的余弦函数模型确定不含刻槽的干涉条纹的分布特征:

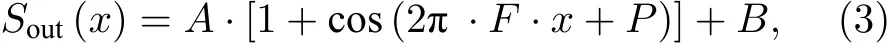
其中,A为振幅,F为空间频率,P为初始相位,B为基线.这四个数据分布特征参数可以通过对不含刻槽数据进行余弦拟合得到,而拟合初始值可以通过对余弦条纹进行FT 计算得到.

步骤3从含刻槽数据中确定刻槽内数据的分布特征值Sin时,由于刻槽区域内为均匀的亮度分布,而刻槽内外的像元数大致相等,因此数据中灰度值在Sin附近的像元点是数量最多的.利用这一特性可以对数据进行直方图统计,选择分布概率最高的区间的数据点,对其灰度值求平均值得到刻槽内灰度特征值Sin的近似估计.

步骤4利用阈值方法初步判断边缘的像元位置,通过合适的阈值保证所得边缘结果都在真实边缘上.这一步可能会有部分边缘点漏判.

步骤5根据边缘初判结果,粗略估计刻槽周期,补充上一步漏判的边缘,得到完整的所有边缘的像元位置.

步骤6在每个边缘附近,按照(4)式所示的函数模型进行逐边缘的分段拟合.其中xn为在第n个边缘附近节选的像元坐标值,A,F,P,B,Sin为数据分布特征参数,由步骤2,3 得到;Rn为第n个边缘的函数模型,其正负代表边缘的上升或下降;bn和cn分别代表第n个边缘的中心位置和坡度,是边缘拟合的目标参数.

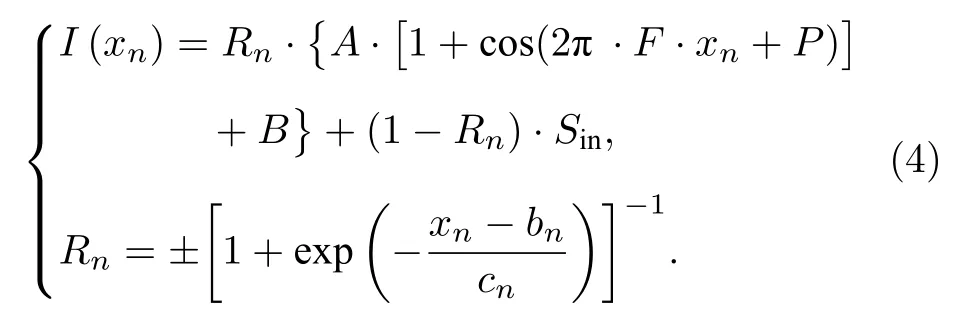
步骤7在上一步cn的拟合结果中剔除一部分异常值,然后进行平均,再将平均后统一的坡度参数代入(4)式的模型并固定,进行对刻槽边缘亚像元位置的第二次拟合.

当对连续采集的多帧图像进行漂移监测时,可以省略步骤4 和5,而以第一帧图像的边缘位置作为初始值直接进行边缘拟合.在得到所有图像中刻槽的边缘位置后,用每帧图像中所有边缘像元位置的平均值作为判断不同图像之间刻槽偏移的依据,可以减小部分随机误差.

3 像面热漂移监测实验

为了验证像面热漂移监测算法的有效性,本文基于近红外多普勒差分干涉仪样机的连续热稳定性测试数据进行了像面热漂移监测实验,样机如图3 所示.样机的前置镜组件、干涉仪真空箱体组件以及条纹成像镜组件安装于同一基板,而探测器被固定于样机外箱体上,样机基本工作参数见表1.干涉仪真空箱体与干涉仪组件之间增加了加热板,加热板为铜板之上贴以加热片组成.加热由PT1000 热电阻提供,连接热控仪对干涉仪组件进行温度控制,热控仪采用PID 控制,干涉仪外箱体有温度传感器监测外界环境温度变化.

表1 近红外实验样机工作参数Table 1.Working parameters of near infrared experimental prototype.

图3 近红外多普勒差分干涉仪样机示意图Fig.3.Schematic diagram of the near infrared DASH prototype.

图3 展示了对4 天的热稳定测试数据进行像面热漂移监测的结果,并与图像采集期间的环境温度变化及图像的相位漂移进行了对比,其中相位漂移是先选取干涉图中央区域的部分条纹,再进行相位反演后取平均相位计算得到后续图像相对第一帧的相位变化,并且利用刻槽漂移检测结果对原始相位漂移进行了校正.

从图4 中可以看出,刻槽漂移与干涉仪温度的变化间保持了较强的相关性,刻槽漂移检测结果的振荡与温度的振荡变化在趋势上基本一致,与相位漂移的振荡也有很高的一致性.将温度曲线与刻槽漂移曲线进行去基线处理后,四天里二者的相关系数分别为0.86,0.57,0.41,0.66,这表明温度的不稳定是造成像面的漂移振荡进而造成条纹相位漂移振荡的主要因素之一.而另一方面,从图4 还可以看出,像面漂移、相位漂移和温度三者常常在长期的基频变化上有较为明显的区别,当温度在振荡之余还保持整体的上升或下降时,相位漂移和像面漂移检测结果有时不能很好地与之相对应,比如在Day 1 的数据中,温度的整体下降在相位和刻槽的漂移中没有体现,在Day 2 的数据中,温度的下降幅度远大于振荡变化的幅度,但相位漂移变化中振荡变化要更明显,而在刻槽漂移中下降趋势更是几乎不可见.这可能是因为由于约束的存在,像面的漂移被限制了,同时还有其他造成相位漂移的因子的作用,比如条纹数的变化、图像的倾斜等,这些因子可能在某些条件下与像面漂移造成的相位变化形成增强或相互制约的关系,使得这三者表现出不匹配的现象.但从相位漂移的校正来看,经过校正,相位的振荡变化基本被消除,基频变化量也有较为明显的减弱,这说明利用像面漂移监测来校正相位具有提高仪器相位反演准确度,进而提高风速反演精度的潜力.

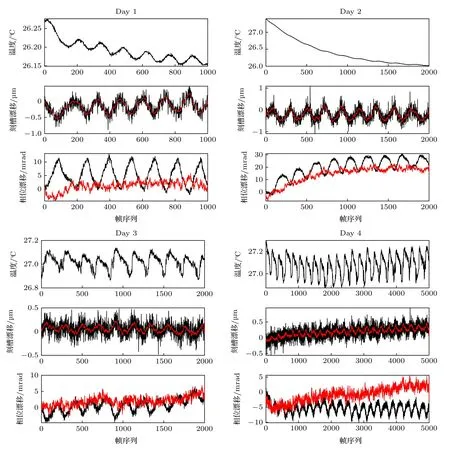
图4 对热稳定测试数据进行像面漂移监测的结果示意.刻槽漂移中,黑色曲线代表原始检测结果,红色曲线代表平滑得到的趋势线;相位漂移中,黑色曲线代表原始的相位漂移,红色曲线代表校正后的相位漂移Fig.4.Schematic diagram of image plane drift monitoring results of thermal stability test data.In the graph of notch drift,the black curve represents the original result,and the red curve represents the smoothed trend line.In the graph of phase drift,the black curve represents the original result,and the red curve represents the corrected phase.

4 像面热漂移监测精度和不确定度分析

刻槽边缘拟合的误差主要来自于两方面,一是边缘拟合中噪声对拟合过程的干扰带来的随机误差,二是拟合所用刻槽内外的数据特征参数与真实值之间的误差.数据分布特征参数包括干涉条纹的振幅、频率、相位、基线以及刻槽内分布特征值,这些特征参数的误差来自于照明、光学系统像差等造成的成像不完善以及噪声的干扰.为了验证刻槽边缘检测算法的精度,本文通过数值仿真来验证图像信噪比和数据分布特征参数误差分别对边缘拟合过程的影响.首先生成理想的余弦干涉条纹数据,然后利用Marr 等[9]所用的卷积方法生成刻槽模拟函数,再生成含刻槽干涉数据的仿真数据,最后给数据加入不同能量的噪声,用生成仿真数据时的数据分布特征参数来拟合边缘;或是固定图像的信噪比,给各项数据分布特征参数分别增加一定误差来拟合边缘.比较拟合出的边缘结果与仿真数据真实边缘之间的偏差,来验证各项参数对最终检测结果的不同影响.

图5 展示了图像信噪比与刻槽边缘检测误差的关系,对不同信噪比的数据进行边缘检测,在每个信噪比下重复100 次数据仿真及边缘检测,观察噪声随机性对结果的影响.图5(a)展示了100 次重复仿真的结果,可以看到,平均误差始终很小,接近于0,但随着信噪比的提升,平均误差更加贴近于0,而且误差的离散程度越来越低.图5(b)展示了不同信噪比下100 次重复仿真结果的误差的标准差,当信噪比约大于30 倍后,误差的标准差可以保持在小于0.05 像元的水平.

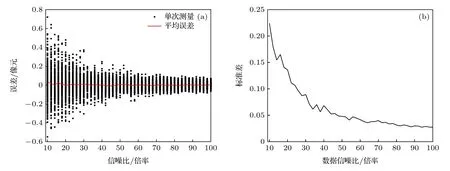
图5 数据信噪比对刻槽边缘检测误差影响示意 (a)100 次仿真实验的结果;(b) 不同信噪比对应100 次重复结果的标准差Fig.5.Schematic diagram of the influence of SNR on notch edge detection error:(a) Results of 100 simulation experiments;(b) the standard deviation of 100 repetitions for different SNR.

图6—图10 展示了边缘拟合过程中所用的各项数据分布特征参数的误差分别对刻槽边缘检测的影响,其中边缘拟合过程中各项数据分布特征参数的误差按真实值的百分比添加.为了同时对比数据信噪比的影响,在刻槽检测之前对数据添加了高斯白噪声,选择了在25 倍和100 倍低、高两种信噪比下进行仿真实验,同样在每个信噪比下重复100 次仿真实验.需要注意的是,刻槽边缘附近图像亮暗对边缘拟合有很大影响,而亮暗取决于数据分布特征参数值自身取值,因此本文中关于数据分布特征参数相对误差影响的仿真只适合作为定性分析参照,而不适合作为详细的定量分析结论.

从图6—图10 中可以看出,在各项数据分布特征参数中,刻槽边缘检测对干涉条纹频率的误差最为敏感,而其他四项参数对检测造成的误差基本处于同一水平,在相同百分比的偏差下,干涉条纹频率造成的检测误差对比其他四项参数可能存在10 倍以上的差距.图中的对比也表明,对这五项特征参数来说,正向偏差与负向偏差造成的边缘检测误差会有不同.从100 次重复仿真的误差的标准差可以看出,数据分布特征参数的偏差对监测误差的离散程度也会产生影响,而每项参数的相对偏差对标准差的影响不尽相同,会出现正负偏差某一边偏大或是偏差某处标准差大于其他位置的现象,不过这种特征可能会随着数据分布特征参数自身数值的变化而变化.通过两种信噪比的对比可以发现,信噪比对检测误差的不确定度有决定性的影响,其影响远大于数据分布特征参数的影响,而在平均误差方面,频率的误差影响很大,其他四项参数对平均误差的影响相对较小.

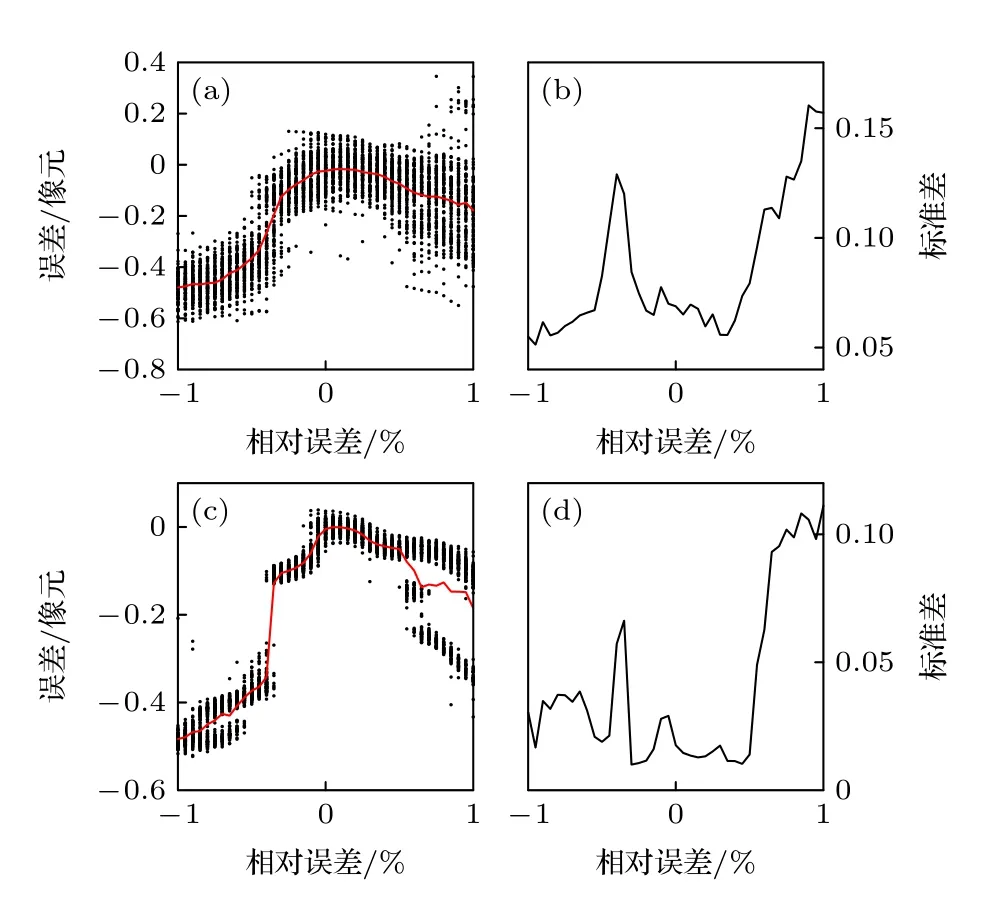
图6 干涉条纹频率的相对误差对刻槽边缘检测误差的影响示意图.黑点代表一次仿真的误差,红色曲线代表100 次仿真的平均误差(图7—图11 同) (a),(b) SNR=25;(c),(d) SNR=100Fig.6.Schematic diagram of the influence of the relative error of the interference fringe frequency on the notch edge detection error.The black points represent the error of single simulation,and the red curve represents the average error of 100 simulations (This is the same as those in Fig.7–Fig.11):(a),(b) SNR=25;(c),(d) SNR=100.

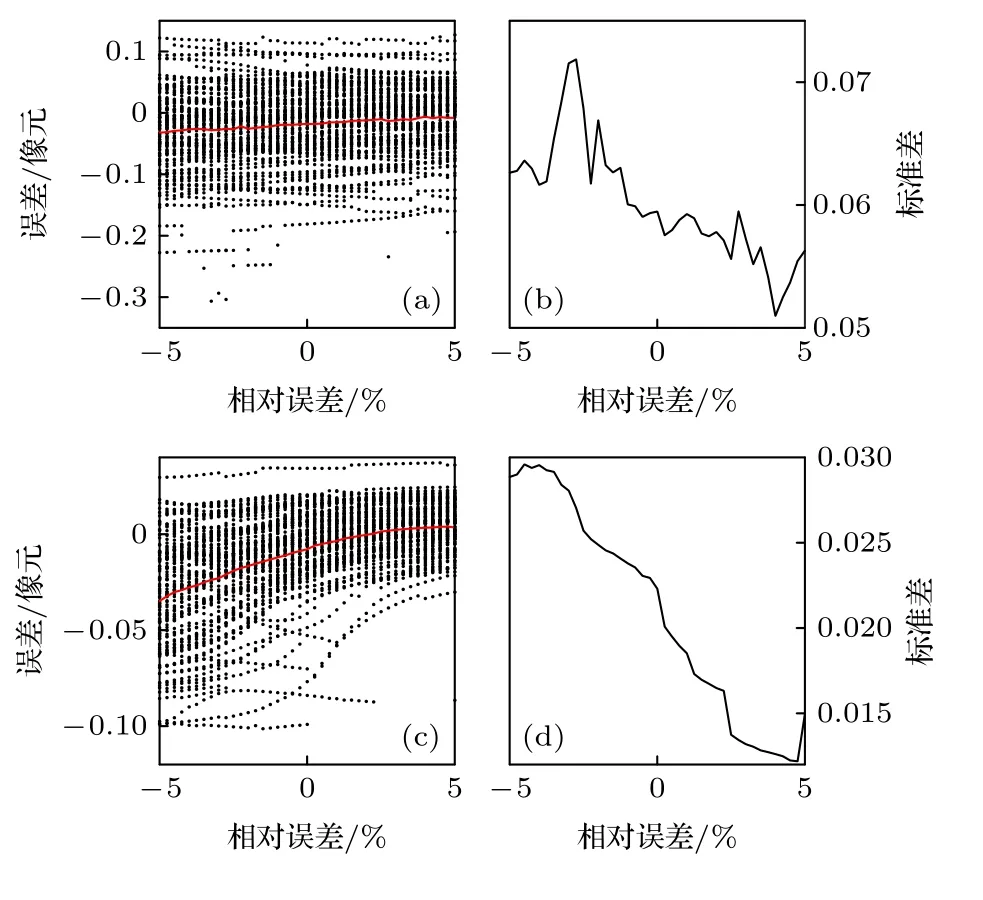
图7 干涉条纹振幅的相对误差对刻槽边缘检测误差的影响示意 (a),(b) SNR=25;(c),(d) SNR=100Fig.7.Schematic diagram of the influence of the relative error of the interference fringe amplitude on the notch edge detection error:(a),(b) SNR=25;(c),(d) SNR=100.

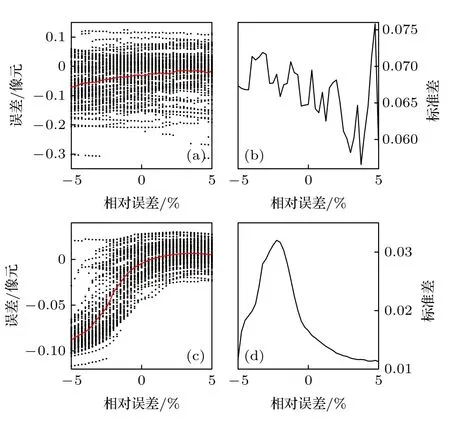
图8 干涉条纹相位相对误差对刻槽边缘检测误差的影响示意图 (a),(b) SNR=25;(c),(d) SNR=100Fig.8.Schematic diagram of the influence of the relative error of interference fringe phase on the notch edge detection error:(a),(b) SNR=25;(c),(d) SNR=100.

综上,图像的信噪比和条纹的频率特征参数的误差对最终刻槽边缘检测结果的影响最为显著,因此要想得到有效的检测精度,需要首先保证图像的信噪比及准确确定干涉条纹的空间频率,在此基础上进一步提高精度的话则需要保证其他四项数据分布特征参数的准确性.结合图5—图10 的仿真对比,可以认为,当条纹频率参数误差在0.5%以内,其他数据分布特征参数误差保持1%以内,图像信噪比在约35 倍以上时,本文的像面漂移监测可以达到高于0.05 像元级别的精度.

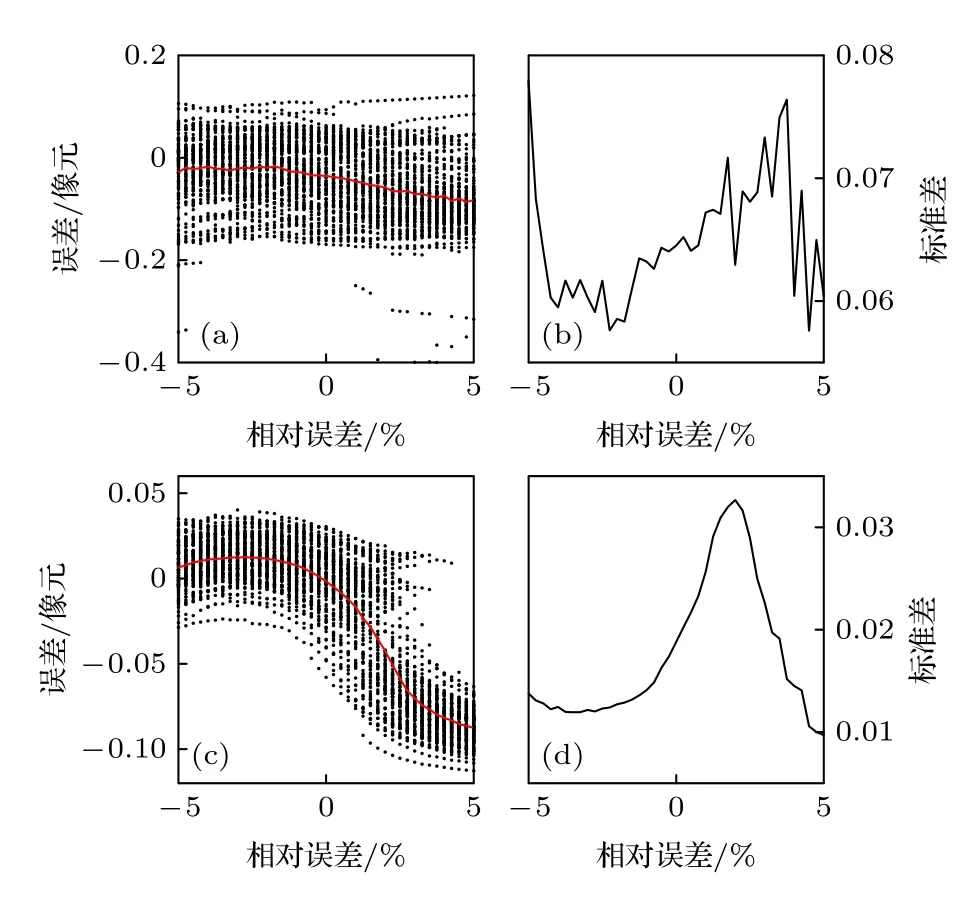
图9 干涉条纹基线相对误差对刻槽边缘检测误差的影响示意图 (a),(b) SNR=25;(c),(d) SNR=100Fig.9.Schematic diagram of the influence of the relative error of interference fringe baseline on the notch edge detection error:(a),(b) SNR=25;(c),(d) SNR=100.

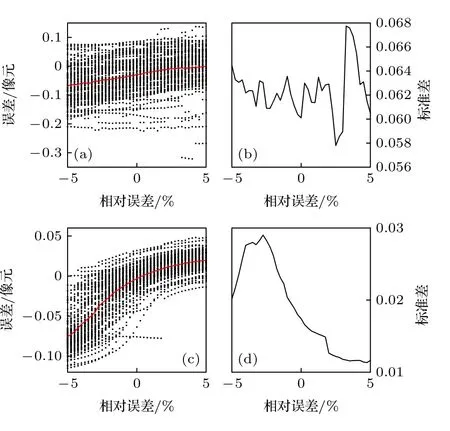
图10 刻槽内灰度分布特征值相对误差对刻槽边缘检测误差的影响示意图 (a),(b) SNR=25;(c),(d) SNR=100Fig.10.Schematic gram of the influence of the relative error of the characteristic gray-scale value in the notch area on the notch edge detection error:(a),(b) SNR=25;(c),(d) SNR=100.

值得注意的是,本文算法以图像数据中所有刻槽边缘位置的平均值作为判断连续帧图像之间漂移的依据,因此理论上可以通过增加数据中的边缘的数量减小结果的随机误差,比如减小刻槽宽度或者提升数据长度.图11 展示了刻槽宽度对检测误差影响的仿真结果,从仿真中可以看出,当刻槽宽度由小变大时,检测误差的标准差有上升的趋势,但这种上升趋势不是特别显著,有明显的随机振荡,在25 倍信噪比下当刻槽宽度较小时甚至出现误差为1 像元的异常情况,表明减小刻槽宽度对提升检测精度有一定提升作用,但这种提升作用不明显,而且可能会增加大检测误差的异常情况出现的机率.提升数据长度在增加边缘数量上的效果与减小刻槽宽度相同,但数据长度的提升受到图像亮度不均匀、干涉图像畸变等因素的限制,当数据有明显的亮度不均匀、畸变存在时,算法得到的数据分布特征参数不再适用于每个边缘,这样会引入拟合误差.

图11 刻槽宽度对刻槽边缘检测误差的影响示意图 (a),(b) SNR=25;(c),(d) SNR=100Fig.11.Schematic gram of the influence of the relative error of notch width on the notch edge detection error:(a),(b) SNR=25;(c),(d) SNR=100.

5 结论

本文用分段拟合的方法对多普勒差分干涉仪图像中的刻槽图案进行了高精度的边缘检测,并以刻槽边缘的亚像元位置作为依据,监测了工作环境温度变化时干涉像面的热漂移.在对近红外实验样机的热稳定测试实验中,像面热漂移对比温度、相位漂移在高频的振荡变化上保持了良好的一致性;而相位漂移在经过基于像面热漂移的校正后基本消除了高频的振荡变化,从侧面证明了热漂移监测的有效性.为了验证本文提出的像面热漂移监测算法的精度,对比了不同数据信噪比水平下边缘检测结果的误差水平,之后又仿真了当拟合过程中所用的干涉条纹的振幅、频率、相位和基线以及刻槽内图像的亮度值等数据分布特征参数与真实值存在一定偏差时,边缘检测结果的误差表现.经过仿真对比发现,图像的信噪比对边缘检测的精度起到支配性的影响,其次是条纹频率的偏差对边缘检测结果也有显著影响,而其他的数据分布特征参数的影响则相对较小.根据仿真实验,当条纹频率参数误差小于0.5%,其他数据分布特征参数误差在1%以内,数据信噪比达到约35 倍以上时,边缘检测的精度可以达到高于0.05 像元的精度,而这样的精度对多普勒差分干涉仪提高风速测量精度具有一定的实用价值.基于验证精度的仿真实验及分析,本文中像面热漂移监测还存在进一步提升精度的潜力,比如通过数据平均合成提升边缘拟合用数据的信噪比,或是用新的数据分析方法得到更准确可靠的数据分布特征参数等.