幅相同调的吸波-对消雷达散射截面减缩超表面设计*

袁方 毛瑞棋 高冕 郑月军 陈强 付云起

(国防科技大学电子科学学院,长沙 410073)

更宽的工作频带和更低的雷达散射截面(radar cross section,RCS)一直是低可探测领域研究的热点,然而这两者往往难以兼顾.鉴于此,本文提出了一种幅相同调的吸波-对消RCS 减缩超表面,通过在宽带范围内同时设计两个单元的反射相位和反射幅度,使目标RCS 在空间域和能量域分别获得10 dB 以上减缩,从而通过叠加获得20 dB 以上的宽带RCS 减缩.仿真和实验结果表明,在两种极化下,幅相同调的吸波-对消RCS减缩超表面可以在6.10—12.15 GHz 频带范围内获得20 dB 以上的RCS 减缩效果,同时10 dB 减缩带宽为4.3—14.2 GHz.所设计的超表面具有减缩幅度大、减缩频带宽、质量轻、单层结构、极化稳定性好、柔性易共形等优点,有望为低可探测材料研制以及低可探测装备性能提升提供新的技术途径.

1 引言

军事目标在雷达探测下实现电磁隐身的主要手段是降低目标雷达散射截面(radar cross section,RCS),两种常用方法分别是设计特殊外形和使用雷达吸波材料涂层.特殊外形设计是在空间域实现电磁隐身,没有能量损耗.例如F-22 和J-20等战斗机特殊的外型结构,可以将入射能量反射到非探测方向,从而降低后向RCS,实现隐身效果.雷达吸波材料是在能量域实现隐身,通过将探测波能量吸收并转化为内能,减少反射波幅度,实现RCS 减缩.对于某些特殊军事目标,尤其是飞行器等,其物体外形和空气动力学有着紧密联系,改变外形意味着其气动性的下降;而传统雷达吸波材料厚度与密度较大,会增加目标的体积和重量,且造价高昂,损耗较大,维护费用不菲.因此,亟需研究更为经济有效的隐身手段来替代传统方法.

超材料是指一些具有自然界中材料所不具备的超常物理特性的人工复合结构或复合材料.由于超材料独特的设计方法和反常的物理特性,使得其成为近几年学术界的研究热点[1−30].超表面作为超材料的二维平面模式,不仅继承了超材料的诸多优良特性,同时还具有重量轻、剖面低、易与装备表面共形等三维超材料不具备的优点,因此受到研究者的广泛关注.超表面对电磁波优异的调控能力使得其在新型隐身材料的研究应用中发挥了巨大优势,并取得了丰硕的成果.

利用超表面降低RCS,主要手段有两种:一种是在空间域重塑电磁波波形,使得主要能量偏折到非探测方向,降低后向回波[3−11];另一种是在能量域将电磁波能量吸收,转化为内能,从而降低反射强度[12−23].随着研究的不断深入,研究人员开始结合上述两种手段来设计RCS 减缩超表面.2017 年,Zhuang 等[24]提出了双频带低散射超表面,通过引入加载集总电阻的交叉偶极子在S 波段实现吸波;通过几何相位单元的旋转在X 和Ku 波段形成相位梯度,造成漫反射,从而实现双频带10 dB 的RCS减缩.2019 年Ji 等[25]在两个相邻的频段采用双层结构,第一层为几何相位单元,在较低频段实现电磁波漫反射;第二层为电阻性频率选择表面(frequency selective surface,FSS),在较高频段实现吸波,相邻的频段最终合并,将10 dB RCS 减缩带宽扩展为13.0—31.5 GHz.2020 年Zhou 等[26]在双层结构基础上又加了一层吸波结构,上层为编码超表面,中间层为FSS,底层为吸波结构,三层结构主要作用于三个相邻的频带,从而将10 dB 减缩带宽扩展为1.85—19.20 GHz.2021 年Leung 等[27]通过在4 个不同频带处设计具有吸波特性的三维结构磁性材料,并利用它们之间的相位差,扩展了10 dB 减缩带宽为3.4—18.0 GHz.上述工作虽然都采用了吸波-对消/散射两种机制,但由于两种机制分别在不同的工作频带起主要作用,因此只能起到扩展带宽的效果,无法在同一频带内获得更高的RCS 减缩.

本文提出了一种单层幅相同调的吸波-对消RCS 减缩超表面,通过在宽带范围内对单元反射幅度和反射相位的联合设计,在同一频带内同时实现能量域吸波和空间域相位对消,从而在获得更低RCS 的同时,兼顾更宽的工作带宽,最终实现了在6.10—12.15 GHz 频带范围内20 dB 以上的RCS减缩,及4.3—14.2 GHz 频带内10 dB 以上减缩,如图1 所示.本文所设计的超表面具有减缩幅度大、减缩频带宽、质量轻、单层结构、极化稳定性好、柔性易共形等优点,有望为低可探测材料研制以及提升低可探测装备性能提供新的技术途径.

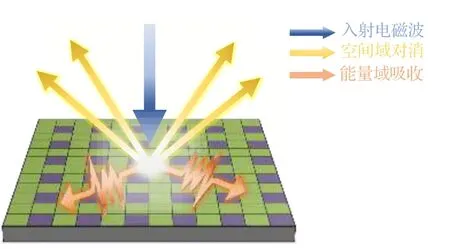
图1 幅相同调的吸波-对消RCS 减缩超表面工作原理示意图Fig.1.Schematic diagram of the working principle of the absorption-cancellation RCS reduction metasurface with the phase-and amplitude-control.

2 幅相同调的吸波-对消超表面设计

2.1 RCS 减缩20 dB 以上的条件

对于一般的底层加载金属板的全反射型超表面,可以等效为一个终端短路的二端口网络,如图2所示.

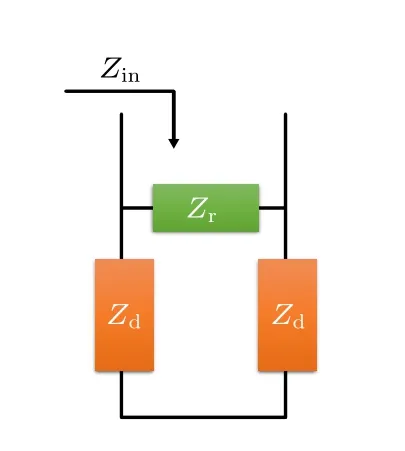
图2 全反射单元等效的终端短路的二端口网络Fig.2.Equivalent transmission line model of the reflected unit cell.

根据传输线理论,可以得到超表面单元反射系数Γ为

其中,Zin为该二端口网络的输入阻抗,Z0为空气的阻抗,

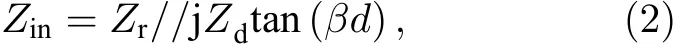
Zr为超表面上层拓扑结构的等效阻抗,Zd为介质的等效阻抗,β为介质的传输常数,β=2π/λ,λ为介质中的波长,d为介质层的厚度,

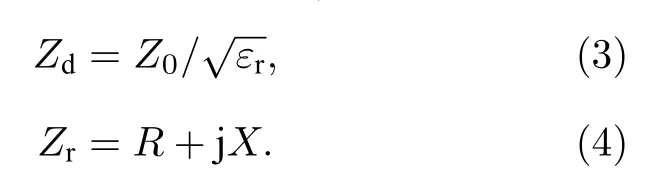
εr为介质层的相对介电常数,因此,单元的反射幅度可以表示为

反射相位可以表示为

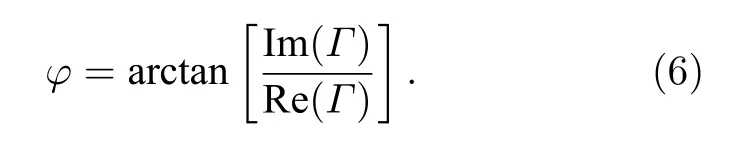
预设单元介质厚度为d=7 mm,选取空气作为介质,相对介电常数为ε0=1,在8,10,12 GHz 频率处,根据(1)式—(6)式,通过Matlab 编程计算,可以得到单元反射相位和反射幅度与超表面上层拓扑结构阻抗R与X的关系,如图3 所示,其中蓝色实线是相位曲线,蓝色虚线是10 dB 吸收曲线,白色虚线是20 dB 吸收曲线.

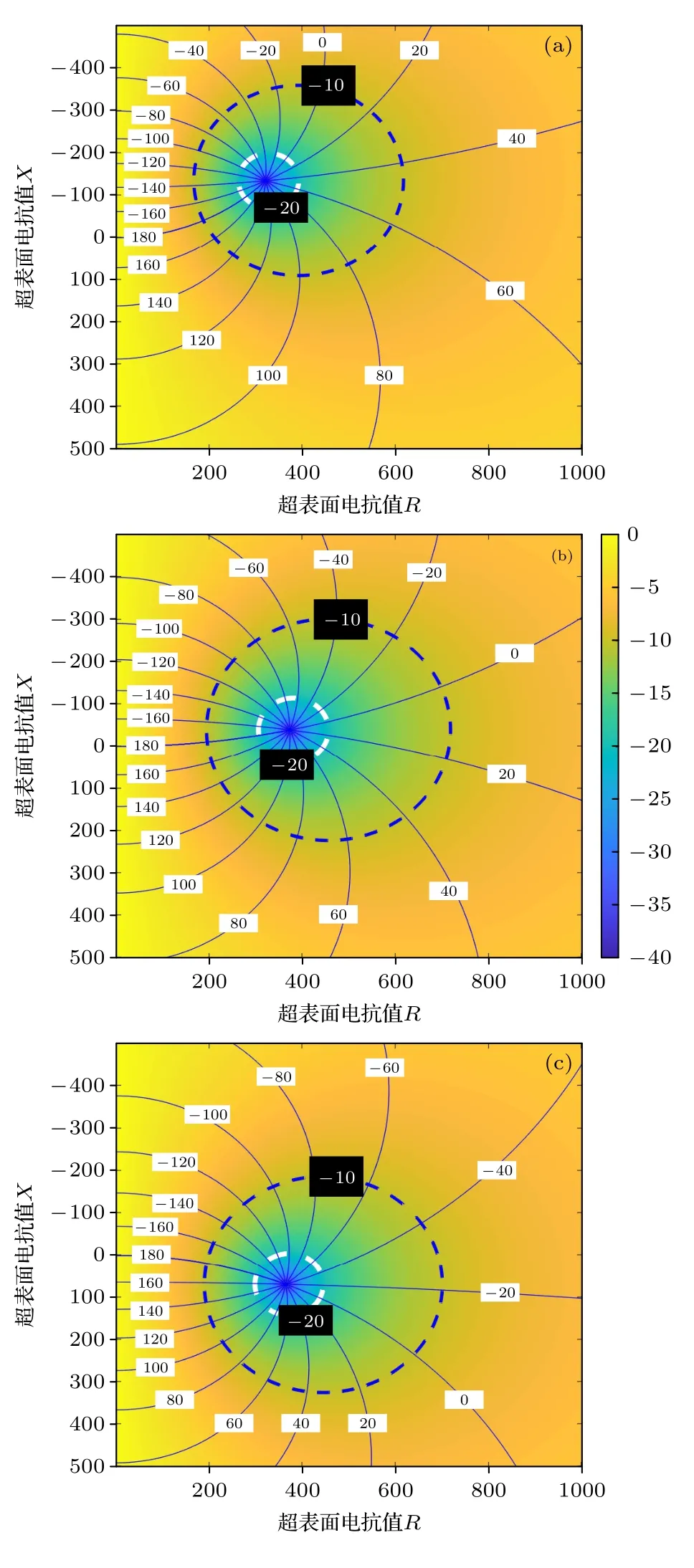
图3 不 同频率 处反 射相位 φ 和 反射幅 度 A 与上层 拓扑结构阻抗R和X 之间的关系 (a) 8 GHz;(b) 10 GHz;(c) 12 GHzFig.3.The relationship among the reflection phase φ,the reflection amplitude A,the impedance of the upper-layer topology R and X at different frequencies:(a) 8 GHz;(b)10 GHz;(c) 12 GHz.

如图3 所示,白色虚线内部为要实现20 dB 减缩时,单元需要满足阻抗条件所对应的区域.可以看出,白色虚线圆圈会随频率变化发生移动.只有当单元阻抗对应的坐标点,同时处于这三个频率所示的白色虚线范围内时,才能实现宽带20 dB 吸收,否则,只能满足个别窄带.从图3 可明显看出,白色虚线的–20 dB 区域远小于–10 dB 蓝色虚线区域,因此,对于只由一种吸波单元组成的超表面而言,实现宽带范围的20 dB 吸波是极其困难的.

当电磁波垂直入射到由两种单元构成的反射型超表面时,超表面的后向RCS 减缩值σr为

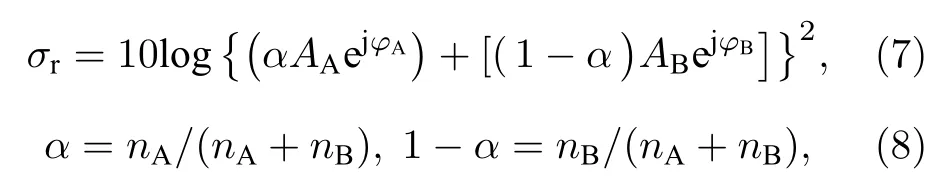
其中,nA和nB分别是整个超表面中单元A,B 的数量,α和1−α分别是单元A,B 在整个超表面中的比例;AA和AB是各自的反射幅度;φA和φB是各自的反射相位,φd=φA−φB是二者的反射相位差值.

如果单元A 和单元B 没有损耗吸收,能量全部反射,则AA=AB=1 .可通过(7)式计算RCS减缩大小与α及φd的关系,如图4 所示.可以看出,当α=0. 5 (即nA=nB)时,相位差取值范围最大.若要获得10 dB 以上的RCS 减缩,需要满足φd=180°±37°,即(143°,217°).这与棋盘结构对消超表面得出的10 dB 相位对消条件一致.但若要获得20 dB 以上的RCS 减缩,则需要满足φd=180°±11°,即(169°,191°).

图4 当单元A 和B 均没有吸收时,RCS 减缩和单元比例α 以及相位差 φd 之间的关系Fig.4.The relationship among the RCS reduction,the parameter α and the phase difference φd,as neither unit A nor B having absorption.

对于传输相位,两个单元在宽带范围满足180°±11°的相位差是极其苛刻的条件.因此在众多单纯使用相位对消的RCS 减缩研究中,达到20 dB 以上的减缩效果都只是个别频点,无法实现宽带工作.单独使用吸波或相位对消中的某一种机制,都很难实现宽带的20 dB 减缩.如果将吸波和相位对消两种机制有效结合,就有望打破宽带20 dB 的RCS 减缩严苛的限制条件.

当单元A 与单元B 都具有10 dB 吸波特性时,即AA=AB=0.316,如图5 所示,在α=0.5时,相位差取值最大.达到20 dB 以上的RCS 减缩则需要两个单元满足180°±37°,这与传统相位对消表面10 dB 减缩所需条件一致.可以看出,如果可以设计两个单元,使它们都具有宽带10 dB 吸波效果的同时,还在该频带具有180°±37°的相位差.利用这两个单元进行组阵,能量域的吸波和空间域的对消就可以同时起效,从而实现宽带范围内20 dB以上的RCS 减缩.

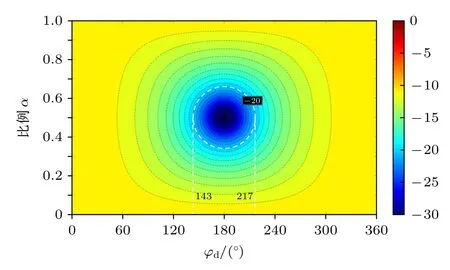
图5 当单元A 和B 均有10 dB 吸收时,RCS 减缩和单元比例α 以及相位差 φd 之间的关系Fig.5.The relationship among the RCS reduction,the parameter α and the phase difference φd with a 10 dB absorption of both units A and B .

2.2 具有宽带反射相位差的吸波单元设计

根据2.1 节的分析,为了使单元具备宽带10 dB吸收效果,即反射幅度A(CST 仿真软件中为|S11|)小于–10 dB,单元上层拓扑结构的阻抗Zr在各频点处的实部和虚部需要满足图6(a)所示关系.提取对应频点R与X的最大及最小值,可以得到图6(b),(c)所示范围.理论上,当Zr在该范围内取值时,可以在所对应频带内获得10 dB 吸收效果.

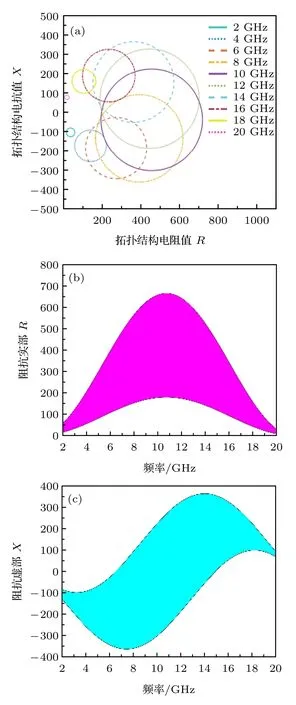
图6 (a) 复阻抗域上不同频率处|S11|=–10 dB 的椭圆曲线;(b) 满足10 dB 吸收的阻抗实部R 的取值范围;(c) 满足10 dB 吸收的阻抗虚部X 的取值范围Fig.6.(a) The elliptic curves of |S11|=–10 dB at different frequencies in the complex impedance domain;(b) the value range of the impedance real part R that meets the 10 dB absorption;(c) the value range of the impedance imaginary part X that meets the 10 dB absorption..

实际上,Zr的取值与拓扑结构关系紧密.利用CST 单元去嵌入仿真,可以获得拓扑结构的R与X曲线.为了设计简便,同时使单元具备极化无关特性,本文选取经典的十字结构作为单元上层拓扑图案.通过仿真优化,十字结构的长度L=12.9 mm,大约为中心频率(12 GHz)的半波长.通过控制变量,分别对十字结构的方阻值和宽度进行去嵌入仿真分析,参数扫描结果如图7 所示.图7(a)为宽度W=4.1 mm 时,方阻值改变的阻抗仿真结果,可以看出,方阻值在40—70 Ω/sq 之间取值时,对实部R影响较大,对虚部X影响较小.图7(b)为方阻值固定60 Ω/sq 时,改变宽度W的阻抗仿真结果,可以看出,W的变化对R和X均有影响.

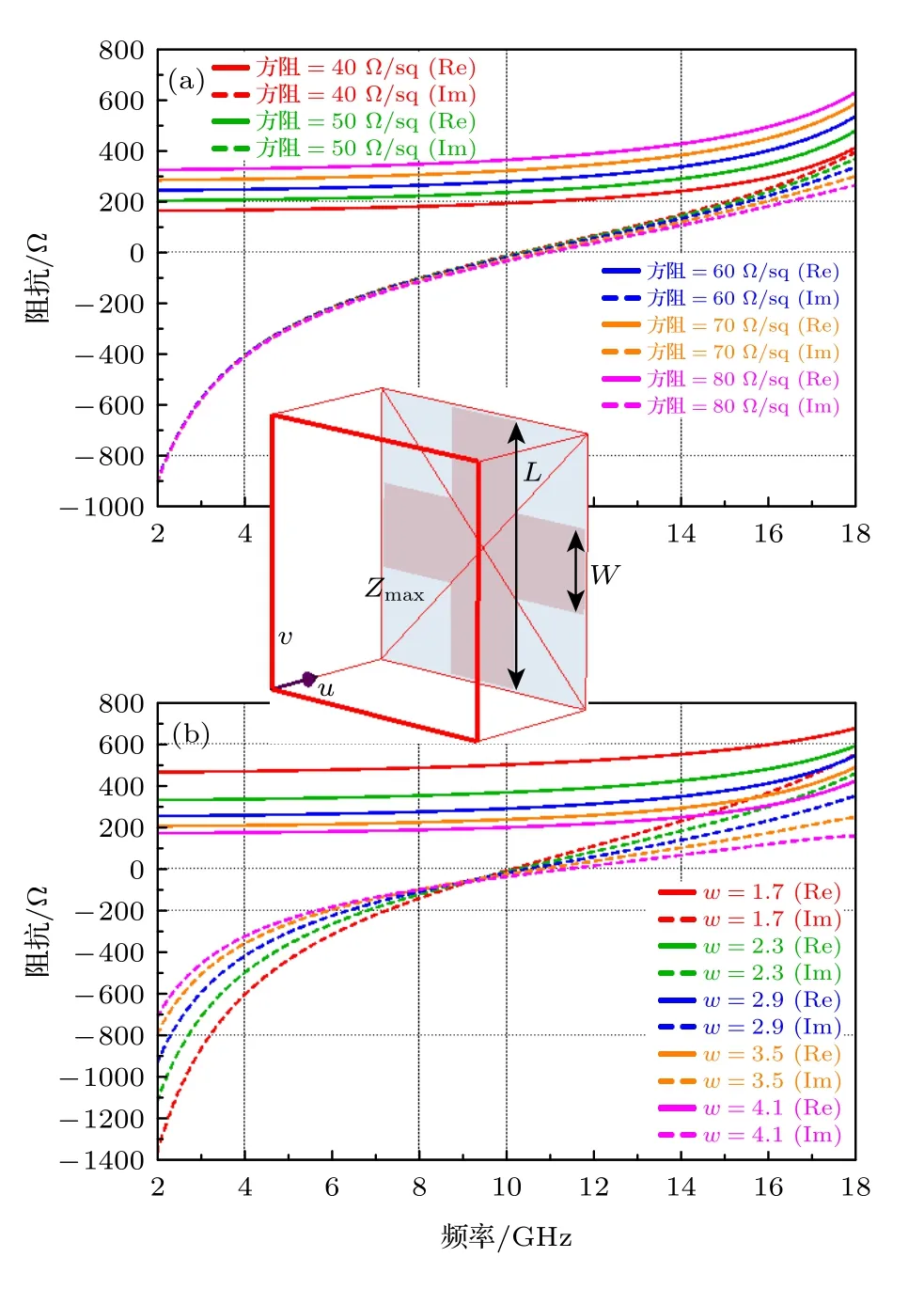
图7 阻抗变化曲线图 (a) W =4.1 mm 时,改变方阻值;(b) 方阻值为60 Ω/sq 时,改变WFig.7.The impedance curves:(a) W =4.1 mm,changing the square resistances;(b) the square resistance being 60 Ω/sq,changing W.

根据图6(b),(c)和图7(a),(b)所示结果,在综合考虑宽度W和方阻值对阻抗变化的影响下,本文首先设计了一种宽带10 dB 吸波单元A,如图8(a)所示,该单元由三层结构组成:底层金属铜反射板、中间空气介质层和上层印刷了电阻膜的柔性PET 薄膜.吸波单元A 的尺寸为P=13.2 mm,空气层厚度h=7.0 mm,交叉十字电阻膜图案的长L=12.9 mm,宽W1=4.1 mm,金属地板厚度为0.018 mm,上层电阻膜的方阻值为60 Ω/sq.所设计的十字单元具备旋转对称性,因此具有极化不敏感特性.为了使超表面具备柔性特征,本文所设计的单元采用了空气作为介质基底,在后期加工测试中,空气层介质可以使用柔性泡沫板代替.

利用CST 商业仿真软件对单元A 进行仿真,结果如图8 所示.可以看出,单元A 在3.96—15.00 GHz内满足10 dB 以上的吸收,但是只有5 GHz 附近一个很窄的范围满足20 dB 以上的吸收.为了在吸波超表面中引入相位对消,从而实现宽带范围20 dB 以上的深度RCS 减缩,需要设计和单元A具有180°±37°的相位差,且兼具一定吸波能力的单元B.在确定单元A 反射相位的基础上,通过仿真优化,设计的单元B 如图8(b)所示.单元B 采用了与单元A 相似的十字结构设计,只是宽度发生了改变,W2=1.7 mm.如图8(c),(d)所示,单元B 在6—13 GHz 范围内具有10 dB 以上的吸波能力,且与单元A 在大约6—12 GHz 内满足180°±37°的相位差.单元A 和单元B 的反射幅度和相位特性满足2.1 节推导的20 dB 以上RCS 减缩条件,因此,2.3 节中将利用这两个单元组成吸波-对消RCS 减缩超表面,进一步验证设计的有效性.

2.3 吸波-对消超表面设计与仿真

利用2.2 节设计的两种吸波单元A 和B,可以组成如图9 所示的超表面.该超表面由20×20 个单元组成,分别由单元A 和单元B 组成的5×5 子阵按照棋盘布局排列,从而实现相位对消特性.利用CST 微波工作室对该超表面进行全波仿真,将仿真所得的单站RCS 与同尺寸金属平板的单站RCS 取差,可以得到该超表面在2—18 GHz 内的RCS 减缩曲线,如图9(b)所示.因为所设计的单元为极化不敏感单元,因此超表面也具备极化不敏感特性,对于水平极化和垂直极化而言,仿真得到的减缩曲线几乎重合.为了表述清晰,图9(b)仅给出了水平极化下的减缩曲线.可以看出,所设计的超表面在6—12 GHz 范围内可以实现20 dB 以上的RCS 减缩,和2.2 节单元设计中满足20 dB 减缩带宽的范围一致.同时,该超表面的10 dB 带宽达到了4.3—14.2 GHz,与优化设计的单元A 的10 dB 带宽相比略窄一点(3.9—15.2 GHz).因此可以说明,本文提出的吸波-对消RCS 减缩超表面设计方法可以在保证10 dB 减缩带宽的前提下,大幅提升20 dB 的RCS 减缩带宽.

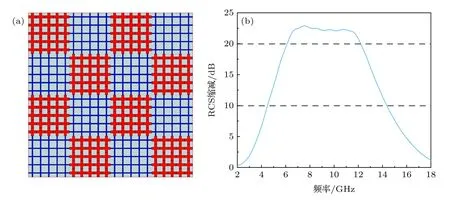
图9 (a) 由单元A 和B 组成的吸波-对消超表面示意图;(b) 该超表面与同尺寸金属平板相比的RCS 减缩曲线图Fig.9.(a) The schematic diagram of the absorption-cancellation metasurface composed of units A and B;(b) simulated RCS reduction curves of designed metasurface compared to the metal plate of the same size.

根据阵列天线理论远场方向图公式,代入单元A 和单元B 的反射相位和反射幅度,可以利用Matlab 计算得到该超表面在特定频率下的远场方向3D 图和2D 图.图10 给出了在特定频率 (10 GHz)处,利用Matlab 理论计算所得的结果与CST 全波仿真所得的结果对比.仿真中出现的副瓣是因为单元间相互耦合的结果,而理论计算中并没有将耦合考虑进去.排除这些耦合引起的副瓣后,可以清晰地看出,理论与仿真结果吻合良好.这也证明了设计方法的正确性及有效性.

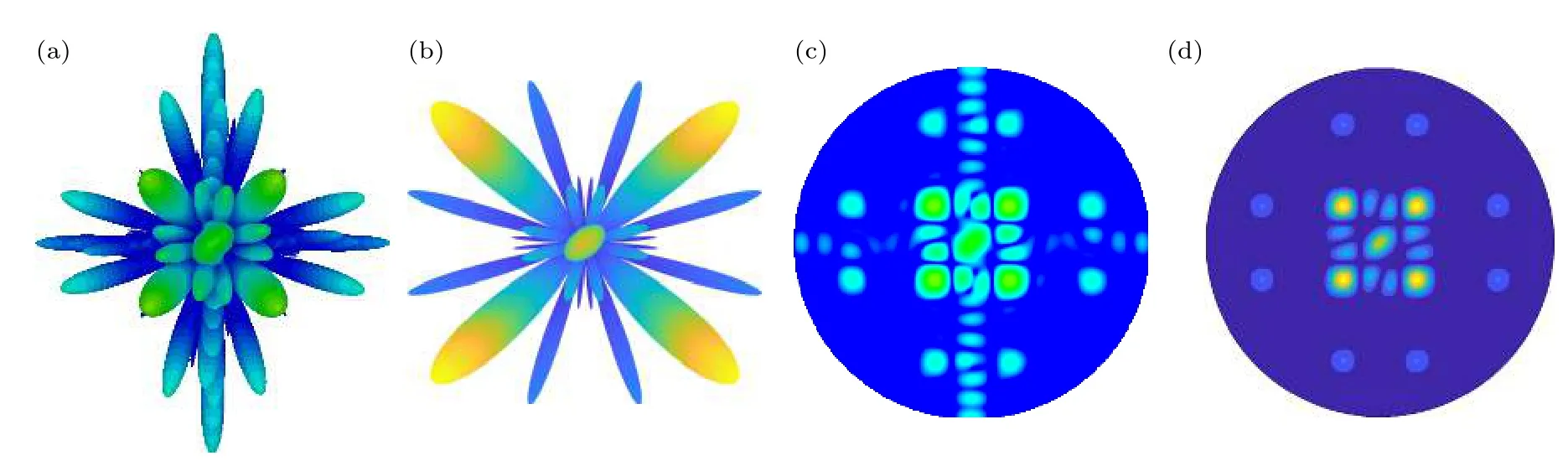
图10 在特定频率10 GHz 处仿真远场图 (a) CST 仿真远场3D 图;(b) Matlab 理论计算远场3D 图;(c) CST 仿真远场2D 图;(d) Matlab 理论计算远场2D 图Fig.10.Simulated far-field pattern at a special frequency of 10 GHz:(a) 3D far-field pattern of CST simulated;(b) 3D far-field pattern of Matlab;(c) 2D pattern of CST simulated;(d) 2D pattern of Matlab.

为了更好地说明所设计超表面的工作特性,图11 给出了在6,8,10,12 GHz 四个频点处超表面仿真远场图以及与等尺寸金属平板的对比.可以看出,所设计超表面继承了单元自身的吸波特性,同时还可以实现单元间因相位差引起的对消.相比金属平板,超表面在平面波垂直入射下的单站RCS得到的大幅度减缩,均在20 dB 以上.

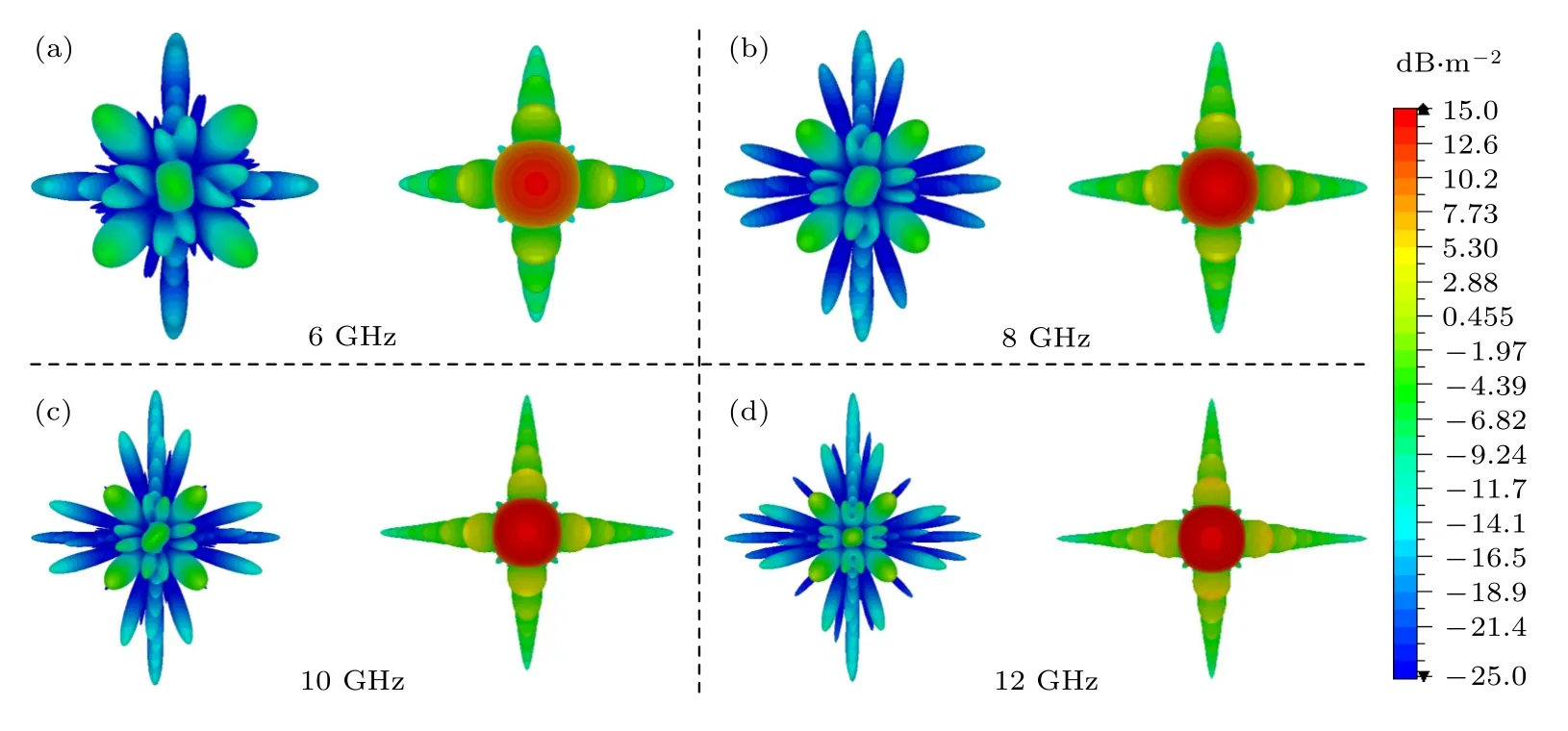
图11 超表面和同尺寸金属平板远场3D 仿真对比图Fig.11.Comparison of 3D far-field patterns of metasurface and metal plate of the same size.

此外,由于所设计超表面具有柔性,还将其作为蒙皮,在金属圆柱上进行共形仿真.在仿真中,y方向设置为周期边界,x和z均设置为“open add space”边界,圆柱半径设置为100 mm.将一个周期的超表面贴附在金属圆柱表面,分别对两种极化的平面波进行仿真,将仿真结果与同条件下的金属圆柱对比,所得的仿真曲线如图12 所示.金属圆柱由于其光滑的曲面结构,自身的RCS 相比金属平面而言已经是一个较低的水平.因此,加载超表面后的RCS 减缩空间并不是很大.即便是这样,从图12 中也可以看出,在水平和垂直极化平面波入射的情况下,所设计超表面依然能实现宽带的10 dB 以上的RCS 减缩.其中,垂直极化的10 dB带宽为4—12 GHz,水平极化的10 dB 带宽为4—15 GHz.同样的,为了进一步说明超表面在共形圆柱情况下的工作特性,图13 给出了主视图和俯视图两张情况下不同频点处水平极化下的3D 远场散射和金属圆柱的对比.可以看出,所设计的吸波-对消RCS 减缩超表面作为圆柱蒙皮也能起到吸波和对消的作用.

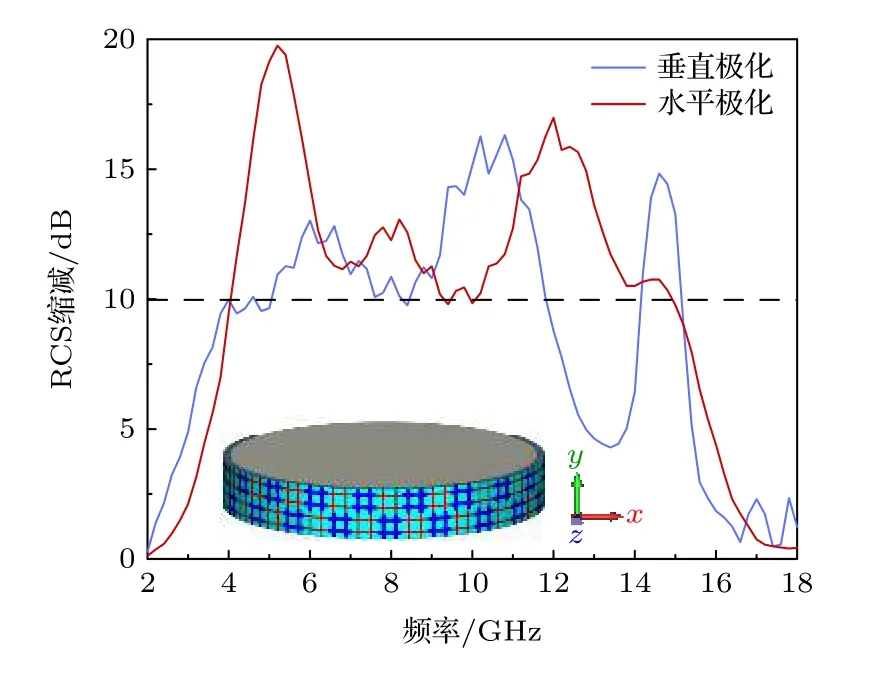
图12 吸波-对消超表面作为蒙皮在圆柱上仿真所得的RCS减缩曲线图Fig.12.The RCS reduction curves of the absorption-cancellation metasurface loaded on metal cylinder.

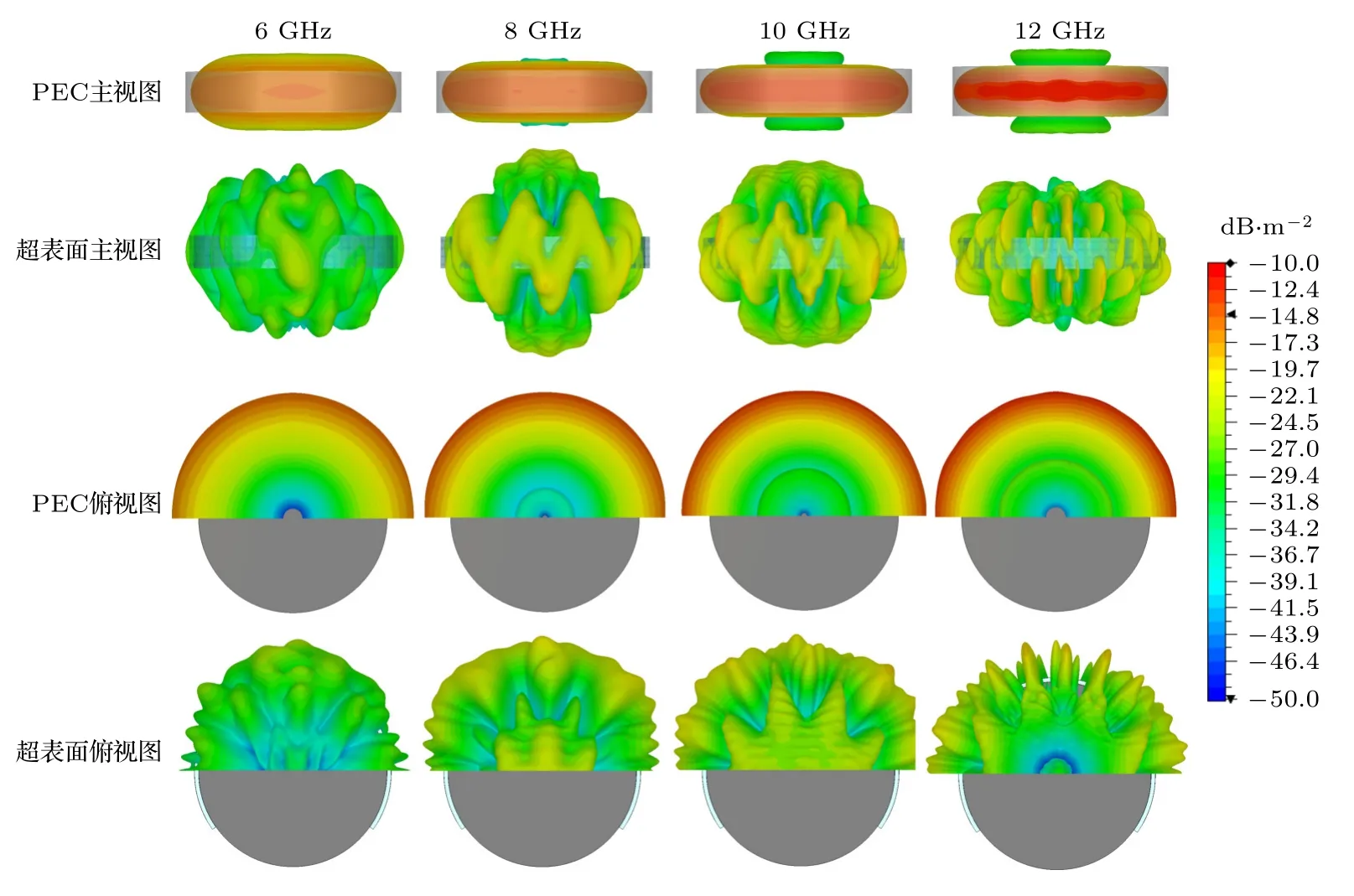
图13 加载超表面蒙皮的圆柱和同尺寸金属3D 远场仿真结果对比图Fig.13.The compared 3D far-field patterns of metasurface loaded on metal cylinder and equal-sized metal cylinder.

3 吸波-对消超表面加工与测试

为了验证理论分析和仿真结果的正确性,加工了柔性超表面样品,并在微波暗室进行了测试,微波暗室环境如图14(a),(b)所示.吸波-对消超表面样品由印刷有电阻膜的PET 薄膜通过超薄(0.01 mm)透明光学双面胶粘贴在泡沫板上,泡沫板粘贴在金属板上组装而成.设计中的空气介质采用了柔性泡沫代替,其介电常数与空气相同,柔性样品如图14(c)所示.可以看出,所设计超表面重量仅为30.2 g,单位面积重量为433.3 g/m2,具备轻量化的优点.

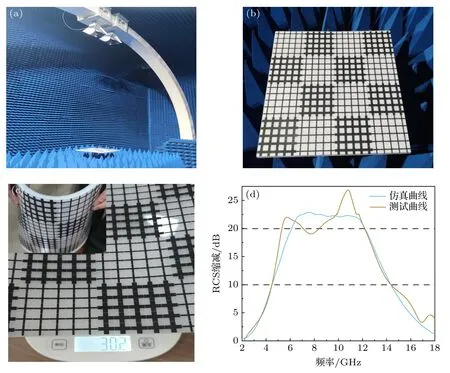
图14 (a) 拱形架暗室测试环境;(b) 待测超表面样品;(c) 柔性超表面样品称重;(d) 仿真结果与测试结果对比曲线Fig.14.(a) Test environment of arched rack;(b) sample of metasurface to be tested;(c) the weight of flexible metasurface sample;(d) simulated and tested curves.

对加工样品在相同条件下进行多次测试,得到如图14(d)所示RCS 减缩曲线,并与仿真曲线做对比.可以看出,10 dB 以上的RCS 减缩测试结果与仿真结果基本吻合,20 dB 以上的RCS 减缩测试曲线在7.0—8.2 GHz 略低于20 dB.造成20 dB带宽不一致的主要原因有两个:一是因为印刷的碳浆电阻膜阻值存在3%—5%的误差,无法保证每一个图案化拓扑结构的方阻值完全等于60 Ω/sq;二是因为样品在使用双面胶组装过程中,不可避免地引入了不规则空气气泡,使得样品厚度不均匀,表面不平整,造成实际单元相位与仿真所得相位略有差异.尽管存在上述误差,所设计超表面依然在宽带范围内实现了接近20 dB 的RCS 减缩(7.0—8.2 GHz 内为19 dB 以上),可以有效说明设计过程的正确性和方法的有效性.因为实验条件有限,只进行了平面结构的吸波-对消超表面测试,没有进行加载该超表面蒙皮的共形圆柱测试.

4 结果讨论

经过理论推导,仿真模拟和样品测试,最终确认本文所设计幅相同调的吸波-对消RCS 减缩超表面的有效性,其在6.10—12.15 GHz 宽带范围内实现20 dB 以上的RCS 减缩同时,10 dB 减缩带宽也可达到4.3—14.2 GHz,一定程度上解决了更宽的减缩带宽和更低的RCS 之间的矛盾.表1 给出了本文与其他类似研究文献的结果对比,大部分研究者利用吸波-对消这两种方法构建超表面来扩展10 dB 的减缩带宽,确实取得了很大的进展,但这些研究都只实现了更宽的RCS 减缩,没有实现更高的RCS 减缩.本文设计的幅相同调吸波-对消超表面,在保证10 dB 的RCS 减缩带宽的同时(相对带宽107%),大大提升了20 dB 减缩带宽(相对带宽66%),既实现了宽带减缩,又实现了深度减缩.同时,相比表中文献,本文的超表面为单层结构,设计简单,易于加工制作.

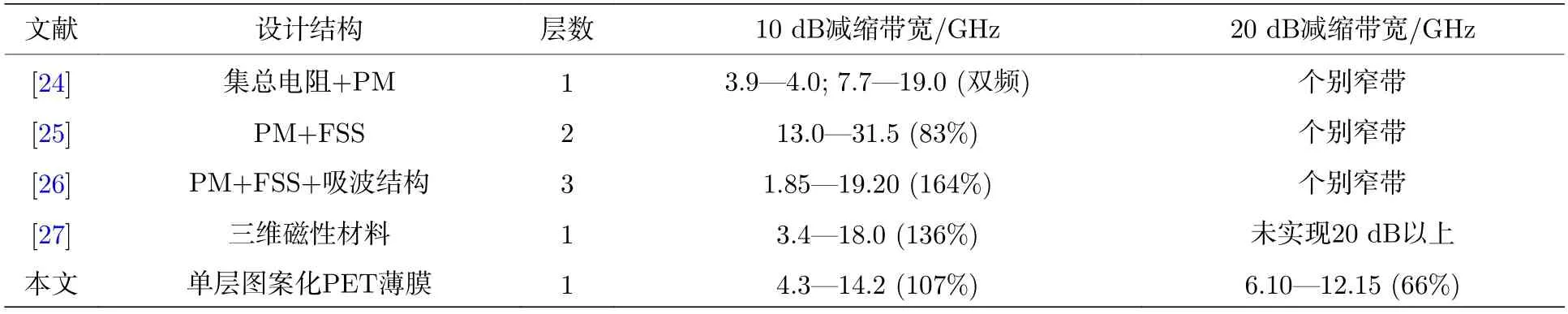
表1 相关文献研究成果比较Table 1.Comparison of related research results.

此外,表2 给出了超表面作为蒙皮和其他圆柱共形超表面研究文献结果对比.对于金属圆柱而言,本身光滑的曲面结构就使其RCS 值较低.因此,大部分RCS 减缩超表面在圆柱上的应用都难以达到宽带10 dB 减缩.本文设计的深度RCS 减缩超表面加载到圆柱表面后,虽然无法达到平面情况下20 dB 以上的减缩,但依然可以实现10 dB以上的宽带减缩,与相关研究成果相比具有较大的优越性.

表2 共形圆柱RCS 减缩文献研究成果比较Table 2.Comparison of related research results for cylinder RCS reduction.

5 结论

本文主要针对幅相同调的吸波-对消RCS 减缩超表面进行研究与设计.首先推导了宽带20 dB以上RCS 减缩的实现条件,然后通过同时设计两种吸波单元的反射相位和反射幅度,最终生成吸波-对消RCS 减缩超表面.理论推导,仿真模拟和实验测试均证明所设计的超表面可以在单层结构下实现宽带范围内20 dB 以上的RCS 减缩,相对带宽达到了66%,同时10 dB 减缩带宽达到107%.将该超表面作为蒙皮加载到圆柱上时,依然可实现两种极化下4—12 GHz (100%)的10 dB 减缩带宽.同时,所设计超表面由泡沫作为介质层,质量轻,易与不规则物体共形,还具备极化不敏感等诸多特性,为新型隐身材料的设计提供了新的思路.