双腔比对折射率法测定气体压力*
2022-04-27刘洋洋胡常乐孙羽2王进2胡水明2
刘洋洋 胡常乐 孙羽2) 王进2)† 胡水明2)
1) (中国科学技术大学化学物理系,合肥 230026)
2) (中国科学技术大学,中国科学院量子信息与量子科技创新研究院,合肥 230026)
搭建了基于气体折射率方法的气体压力测量装置,测量区间为10—100 kPa,采用双腔比对方法对装置进行了检验.通过将两个真空腔体分别控温,并且真空连通,保证了两个腔内气体压力相同.以高纯氮气(6N)为气体介质,在不同气体压力条件下,得到了双腔对比测量的初步结果.结果显示,基于光学方法的气体折射率压力计重复度高于30 × 10–6,显著好于商用电容式薄膜压力计,说明该方法具有很大潜力.本文还分析了测量中的误差来源,并计划通过改进系统设计以提高测量精度.
1 引言
1670 年以来,低压区(1 Pa—100 kPa)的气体压力基准测量一直采用水银压力计,测量依据的公式为P=ρgh,其中h是水银柱的高度,g是水银压力计所在位置的重力加速度,ρ是水银密度.重力加速度和水银密度的测量精度较高,因此水银柱高度h的测量精度决定最终气体压力的测量精度.目前世界上水银柱高度测量最精确的是由美国国家标准局(National Institute of Standards and Technology,NIST)研制的超声水银压力计(ultrasonic interferometry manometer,UIMs),其压力测量的不确定度为[1,2].使用水银压力计进行测量的方法以其测量精度高的优点,至今没有被其他测量方法取代.
近些年,随着实验方法和理论计算精度的提高,气体压力的测量有望通过原子或分子的微观性质与激光频率联系在一起[3,4],而气体折射率n就是其中的桥梁.气体压力通过气体状态方程与折射率n联系在一起,而充满气体的谐振腔纵模的共振频率与气体的折射率有关,因此气体压力的测量即转换为谐振腔腔长的测量.气体折射率压力计的相关研究已开展近十年时间,美国NIST 研究组研制的基于氮气的折射率压力计,将氮气折射率测量精度提高到了3×10–10[5−9].
本文利用气体折射率压力计的测量原理,搭建了首台利用光学谐振腔测量气体压力的实验装置,并与商用精度最高的薄膜压力计做比对,实现了气体压力测量精度高于100 ×10–6的结果[10],分析认为此结果的误差主要来源于薄膜压力计的测量误差.本文主要介绍了如何利用双腔比对测量方法消除薄膜压力计的测量误差,分析讨论了气体折射率压力计的测量精度及光学方法测量气体压力的误差来源,最后给出了实验结果和未来工作计划.
2 实验装置
本文的实验装置光路示意图如图1 所示,Laser1和Laser 2 波长均为1566 nm,通过PDH 锁频方法分别锁定在两个独立的光腔(1#,2# Cavity)上,Laser 1 为窄线宽激光器(NKT Photonics),激光线宽小于1 kHz,Laser 2 为自制外腔式半导体激光器(external cavity diode laser,ECDL),激光线宽约100 kHz.两光腔结构相同,均为ULE(ultra low expansion)材料制作而成,长度均为10 cm,腔镜反射率约为99.9%,计算得到光腔自由光谱范围为1.5 GHz,线宽约500 kHz,而实验测量得到腔模线宽为400 kHz,与计算值基本一致.ULE 光腔放置在一个圆形不锈钢材料加工成的真空腔体内,不锈钢真空腔体放置在一个铝合金材料制成的圆筒内,铝合金圆筒外面缠硅胶加热片控温,不锈钢腔体外放置测温铂电阻温度计来测量腔体温度,如图2 所示.所使用的铂电阻温度计均在中国计量院校正过,精度约为5 mK.两真空腔体之间用一段真空软管连接,以保证两腔体内气体压力完全一致,中间连接一个薄膜压力计(Inficon,Cube CDGSci,精度为读数的0.025%)来获得粗略的充气压力.实验过程中不断往两个腔体内充入高纯气体,测量Laser 1 和Laser 2 的绝对频率,计算得到腔体内气体的压力.
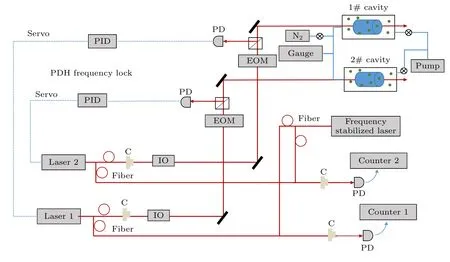
图1 双腔比对测量光路示意图,Laser 1 为NKT 窄线宽激光器,Laser 2 为自制ECDL,IO 为隔离器,EOM 为电光调制器,counter为频率计,C 为光纤耦合头,PD 为光电探测器Fig.1.Schematic diagram of the optical path of the dual cavity comparison measurement.Laser 1 is an NKT narrow linewidth laser,Laser 2 is a self-made ECDL,IO is an isolator,EOM is an electro-optic modulator,counter is a frequency meter,and C is an optical fiber coupler.
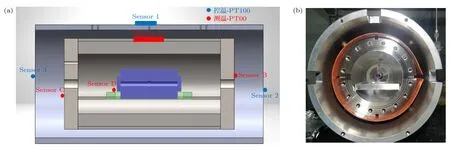
图2 (a) 真空腔体结构示意图,Sensor 1—3 为控温铂电阻温度计,Sensor A—D 为测温铂电阻温度计;(b)真空腔体实物图Fig.2.(a) A schematic diagram of the vacuum cavity structure,in which sensor 1–3 are temperature-controlled platinum resistance thermometers,and sensor A–D are temperature-measured platinum resistance thermometers;(b) the physical map of the vacuum cavity.
3 分析与讨论
3.1 控温系统
腔体温度控制分三部分:铝合金腔体侧面、两侧盖板,分别单独控温.测试均在标准大气压下进行,由于腔体存在漏热,因此实验中根据Sensor A,B,C 的温度读数来调节外层控温的温度点,使得Sensor A,B,C 三个测温温度计读数一致,再比较Sensor D 与他们的差别.温度控制测试结果如图3所示,从图中可以看出,在数小时的测量时间内,A,B,C,D 四个Sensor 读数差别在铂电阻温度计校正精度以内,说明腔体内外温差小于5 mK,最终传递到气体压力上,对压力测量的影响约为20×10–6,对应气体压力约为2 Pa.
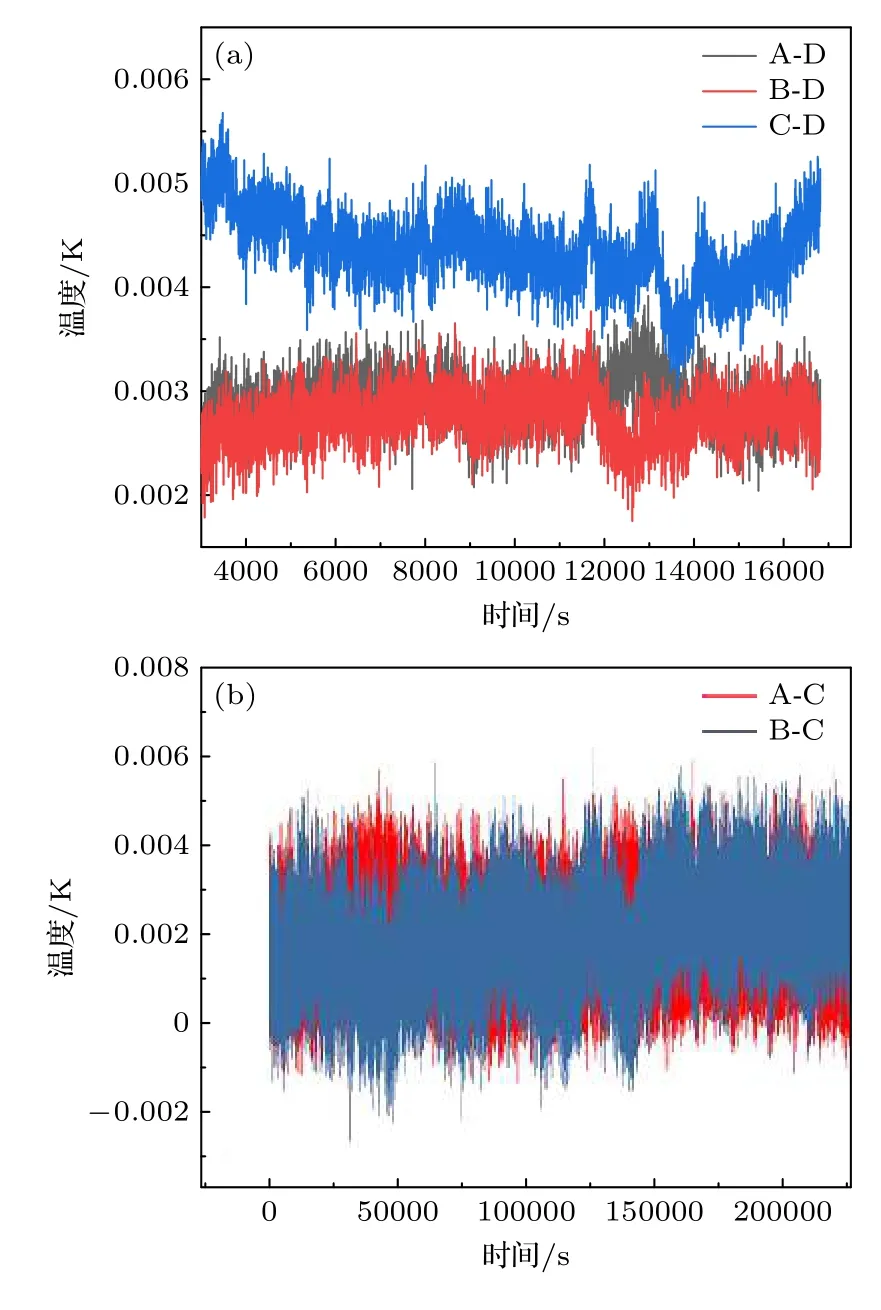
图3 (a)1#腔体控温结果;(b) 2#腔体控温结果,其中A 为腔体侧面温度,B,C 为两端盖板温度Fig.3.(a) Temperature controlled result of 1# cavity;(b) temperature controlled result of 2# cavity,where A is the temperature of the side of the cavity,B and C are the temperatures of the cover plates at each end.
3.2 ULE 腔漂移测试
真空测试过程如下:将腔体抽至真空(分子泵加机械泵,抽气10 h 以上),然后用角阀将其封闭,把两台激光器分别锁定在两个腔体上,再分别与另一台锁定在超稳腔(频漂约为0.1 Hz/s)上的窄线宽激光拍频,由拍频频率可计算得到两台激光的频率.测量一段时间拍频频率,对绝对频率值进行线性拟合,即可得到光腔的频率漂移.利用上述方法,测量得到1#腔的频率漂移约为0.6 Hz/s,2#腔频漂约为0.4 Hz/s,此频率漂移包含ULE 光腔的频漂及真空腔体漏气、放气等因素.在气体压力测量实验中,10 kPa 氮气气体对应光腔纵模绝对频率变化约为5 GHz,测量时间约为1 h,可计算得到腔体频漂约为2 kHz,传递到压力测量上,对气体压力的影响约小于0.01 Pa.
ULE 腔温漂测试方法如下:将激光器锁定在ULE 纵模上,改变腔体控温温度,测量ULE 频率漂移大小,即可得到ULE 光腔的温漂系数.在本实验当中,初始腔体温度为25.32 ℃,稳定了1 d以上,再将控温温度升至26.85℃,同时测量锁频激光的绝对频率,如图4 所示.红线为最后一段绝对频率的线性拟合,斜率约为0.3 Hz/s,与空腔时频率漂移一致,说明腔体温度已平衡.整个变温过程,腔体温度变化约为1.5 K,对应激光频率变化约为1 MHz,相对频率变化约为5 ×10–9,因此计算得到,在26℃温度附近,ULE 腔体的膨胀系数约为3 ×10–9K–1.实验测量过程中,光腔的温度变化小于20 mK,由此导致的腔长改变所对应的激光频率变化约为10 kHz,传递到压力测量上,对气体压力的影响约为0.02 Pa.
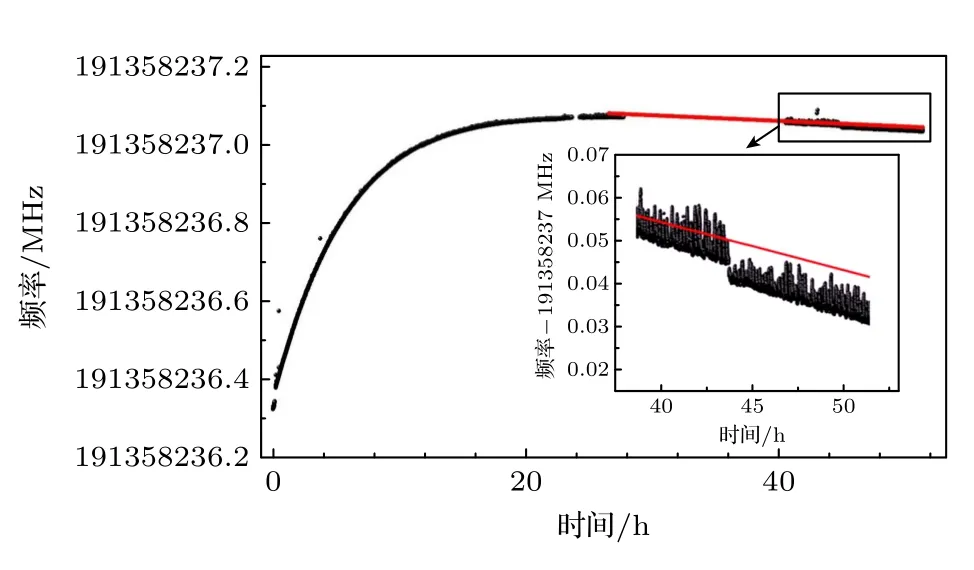
图4 锁频激光频率随时间的变化Fig.4.Frequency of frequency-locked laser varies with cavity temperature.
3.3 压力测量
实验以高纯氮气作为介质进行重复充气测量,测试的结果如图5 所示.实验中测量某个压力P下锁频激光的绝对频率,先计算气体折射率,再计算气体压力.折射率由下式给出[10]:
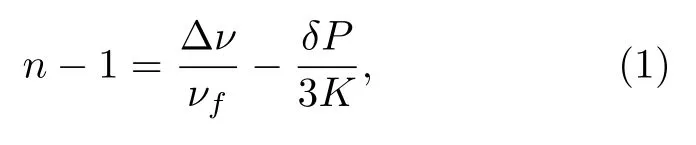
其中,n为折射率,∆ν为充气前后激光绝对频率变化,νf为充气后激光绝对频率,δP为充气前后压力变化,K为ULE 材料体积模量.计算压力的公式[11]为
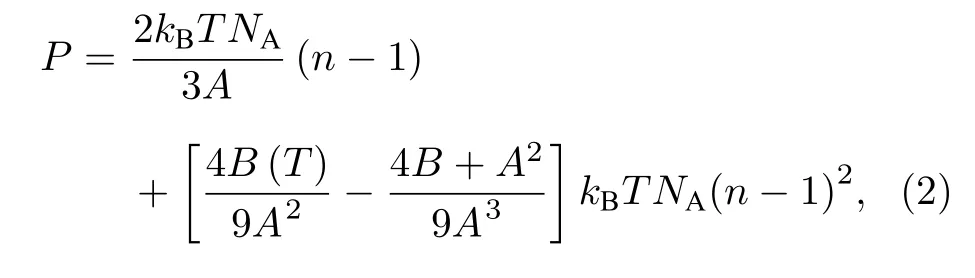
其中,P为压力,kB为玻尔兹曼常数,T为温度,NA为阿伏伽德罗常数,B(T)为第二维里系数,B为第二介电维里系数,A为摩尔极化率.图5 中纵轴为由1#腔和2#腔得到的压力值差,及1#腔得到的压力与薄膜压力计读数之差,横轴为由1#腔得到的压力值.
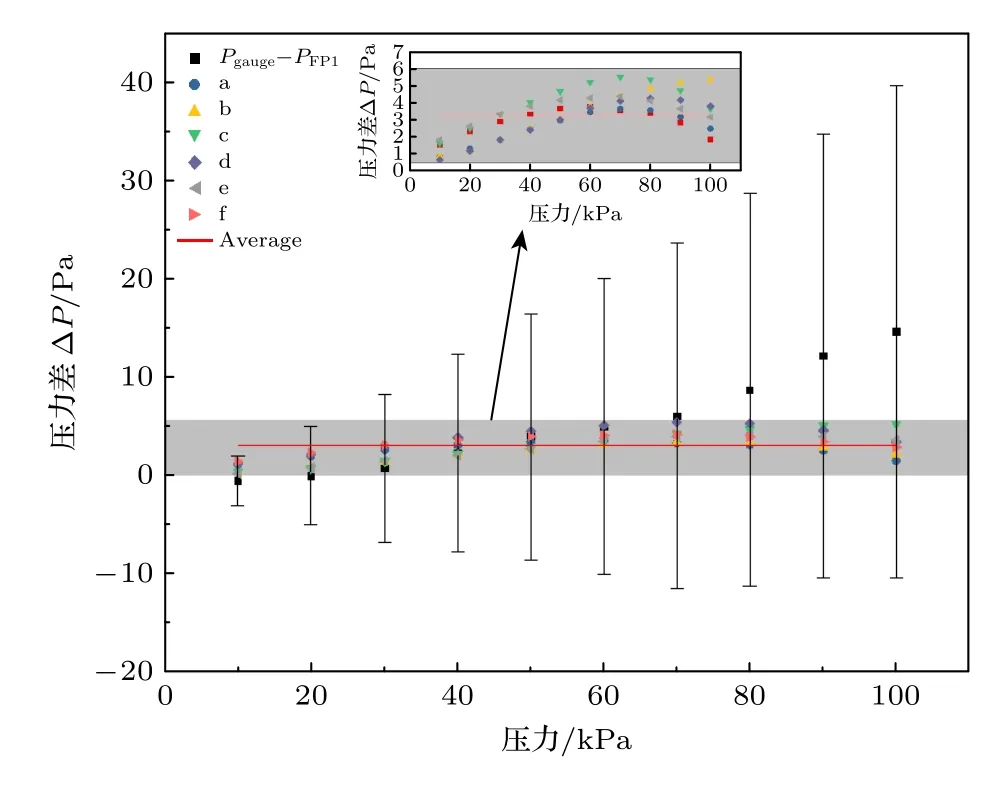
图5 双腔比对压力测量结果,其中,彩色点代表的是双腔测量得到的气体压力之差,a—f 共6 组重复实验,黑色代表的是其中一次腔体测得的气体压力与薄膜压力计读数之差,红线为双腔结果之差的平均值∆P=3.0±3 PaFig.5.Comparison of the pressure measurement results of the dual cavities,where the colored dots represent the difference between the gas pressures measured by the two cavities,a to f totals 6 sets of repeated experiments,and the black represents the difference between the reading of pressure gauge and the gas pressures measured by one of the cavity,the red line is the average value of the pressure measurement results of the dual cavities ∆P=3.0±3 Pa.
原子极化率与入射激光频率有关,可以表述成入射激光角频率ω的多项展开式,包括静极化率以及各项极化率色散系数[12].氮气静极化率理论计算精度与实验测量精度均不高,然而极化率色散系数及633 nm 处的极化率实验测量值的精度足够,因此可先计算出氮气的静极化率,再计算得到1566 nm 处的动态极化率,其他气体相关参数则来自理论计算[13−15],体积模量值来自ULE 参数[11],温度T来自外腔测温sensor 读数,δP来自代入薄膜压力计读数.
3.4 实验结果与误差分析
从图5 可以看出,双腔比对测量重复度高于30×10–6,说明双腔比对测量方法可用于测试光学方法测量气体压力的测量精度.目前这套装置的测量精度高于30 × 10–6,显著好于薄膜压力计的.而双腔测量气体压力的绝对值有约30 × 10–6的偏差,说明这套装置中还存在一定的系统误差,根据之前文章中的误差分析可知,这个系统误差主要来自于腔内气体的温度随着充气压力的改变而发生的变化[10].图6 所示是实验过程中不锈钢真空腔体外侧铂电阻温度计所测量到的腔体温度变化,其中黄色部分为充气过程,绿色部分为充气稳定时.从图5中结果可以看出,在阶段性充气的过程中(图5 中黄色部分),温度是一直在变化的,压力每增加10 kPa,温度变化约为1 mK,当阶段性充气结束时(图5 中绿色部分),温度趋于稳定,这说明腔内气体温度也会随着充气过程中气体压力的改变而发生变化,幅度约为10 mK,对应气体压力变化可达30×10–6.充气过程中腔体内部温度的变化来自于外部抽气端管道真空件的漏热,漏热系数与管道横截面积、材料有关,当腔体内充入不同压力的气体时,腔体的导热系数会随之改变,因此造成腔内气体温度的阶段变化趋势.下一步工作计划是优化外层控温结构,保证外层温度稳定性;另一方面抽气管道替换为更细的管路,以减小管路的横截面积;此外还考虑选用导热系数较小的管道材料,例如聚四氟乙烯等,以减小外部管道的漏热系数.
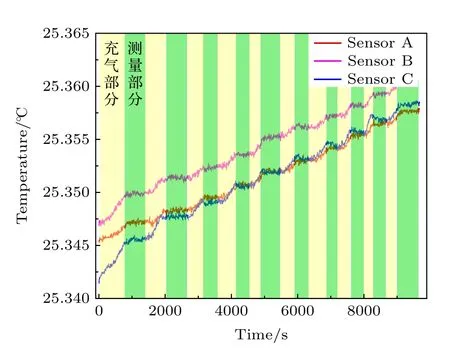
图6 充气过程中测温sensor 读数,其中黄色部分为充气过程,绿色部分为充气稳定状态Fig.6.The readout of the temperature sensor during the inflation process.The yellow part is the inflation process,and the green part is the duration when the inflation is stable .
4 结论
本文研究采用双腔比对测量方法,消除了薄膜压力计的测量精度误差,测试了气体折射率压力计的重复性.比对结果显示,两个腔的测量一致性好于30 × 10–6,误差主要由充气过程中腔体温度变化带来.下一步的改进主要有两点:首先对腔体控温结构进行改进,更换直径更小的气路和选用导热系数更小的材料,以减少气路管道的漏热;其次,在真空腔内放置测温sensor,实时测量得到腔内气体温度,延长充气和测量时间,并监视腔体温度变化,以得到温度稳定时气体的真实温度.
