双圆弧斜齿齿轮泵泄漏研究及最佳间隙设计

董庆伟，刘理想，李阁强

（河南科技大学 机电工程学院，河南洛阳 471000）

0 引言

双圆弧斜齿齿轮泵比普通渐开线齿轮泵不仅额定转速和压力更高，而且流量脉动低、无困油[1]，其性能更加适合航空航天系统，可以作为航空发动机中燃油泵和主油泵，为发动机提供压力和流量以及为高压油增压，同时，这种泵在高速高压工况下运动存在着径向力不平衡、油温过高、泵体结构变形等问题，造成齿轮泵泄漏，从而导致齿轮泵容积效率变低以至满足不了工业要求。而减小泄漏的本质是对齿轮泵轴向和径向配合间隙的控制，既要保证泵的泄漏量少又不能出现刮壳、滑动轴承或者浮动侧板的磨损等现象。为此，YOSHIHARU[2]研究了内啮合齿轮泵的内泄模型，把泄漏间隙看成一个关于压差的变量，给出了计算径向泄漏计算公式。XU等[3]研究了高温齿轮泵的流量控制技术，考虑了其泄漏对控制的影响，给出了径向和端面的泄漏模型。周洋[4]通过对静压滑动轴承的结构设计进行径向间隙补偿。李书仪[5]对滑动轴承内部流场进行了仿真分析，优化了滑动轴承的结构。李玉龙[6]提出了一种无轴向泄漏的新结构来解决轴向泄漏问题。目前，对双圆弧斜齿轮泵的泄漏流量理论计算方法及最佳配合间隙计算方法尚无系统的理论分析，国内更没有相关产品。

本文以25 MPa、10 000 r/min高速高压工况下的双圆弧斜齿轮泵为研究对象，其主要参数为：进油口直径17 mm，出油口直径11 mm，齿数7，模数 3，齿宽 16 mm，压力角 14.5°，螺旋角 28°，中心距21.01 mm。综合考虑了原始径向间隙、原始轴向间隙、油液黏度、径向不平衡力对齿轮轴挠度变化的影响、泵体变形等因素对齿轮泵配合间隙的影响，建立泄漏数学模型，给出计算最佳配合间隙的公式。然后利用FLUENT软件模拟出实际工况下齿轮泵内部流体运动情况，通过理论流量与模拟仿真流量对比分析，验证了泄漏模型的正确性，为齿轮泵结构优化提供理论依据和工程指导。

1 齿轮泵内泄漏模型的建立

形成齿轮泵密闭容积的零件中，齿轮为运动件，泵体和前后盖板为固定件。运动件与固定件之间存在间隙，由于吸、压油腔存在压力差，因此必然存在缝隙流动，即泄漏。齿轮泵泄漏模型主要由以下5个部分组成。

1.1 径向间隙泄漏

双圆弧斜齿齿轮泵径向泄漏可看作层流流动，因此利用平行平板间隙流动理论来计算泵体与齿顶的泄漏[4]，对于圆弧齿轮泵，其径向泄漏为：

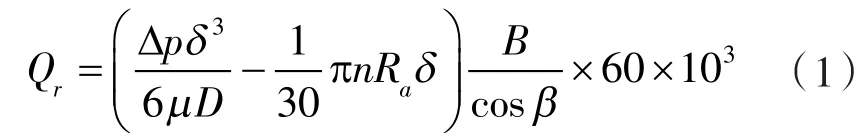
式中 Qr——径向泄漏流量，L/min；

Δp——进出口压差，Pa；

δ——径向间隙，m；

μ——动力黏度，Pa·s；

D——齿轮泵过渡区齿顶总宽度，m；

n——转速，r/min；

Ra——齿顶圆半径，m；

B——齿宽，m；

β——螺旋角，（°）。

1.2 端面间隙泄漏

主从动齿轮端面与轴承端面存在间隙，在压力差的作用下使油液从高压处向低压处流动，由文献[7]知齿轮泵理论端面泄漏量为：

式中 Qf——断面泄漏量，L/min；

δ2——端面间隙，m；

m——模数；

z——齿数；

R——分度圆半径，m；

Ri——齿根圆半径，m；

θx——每个齿腔对应的包含角度，θx＝2π/z；

Rz——滑动轴承内圈半径，m；

Δpx——每个对应齿腔压力差，Pa。

1.3 液压油黏度对泄漏的影响

1.4 齿轮轴挠度变化对泄漏影响

由于齿轮泵进出油口存在压差作用，使齿轮由出油口压向进油口，齿轮轴在不平衡径向力的作用下发生挠度变形，实际工作中，挠度变形尺寸会占据部分径向间隙，必须加以计算以避免工作中出现严重刮壳，根据材料力学和挠度变形的计算式[9]得到齿轮轴的挠度变形量为：

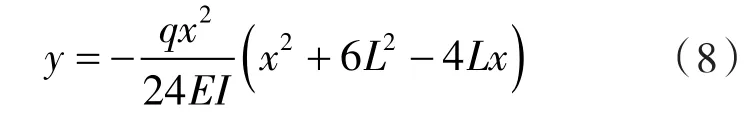
式中 y——挠度值，mm；

q——轴径上所受的分布载荷，N，q＝F/（2L）；

F——径向载荷，N；

E——材料的弹性模量，MPa；

I——轴截面的惯性矩，I＝（πd4）/64，mm4；

x——径长度中心到对应齿轮端面的距离，mm，此处 x＝L/2；

L——轴径长度，mm。

齿轮泵工作中，径向力补偿方式为静压滑动轴承补偿，从动齿轮受到的不平衡径向力F最大，可以近似计算为：

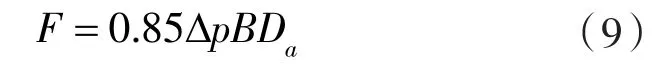
式中 Da——齿顶圆直径，m。

根据齿轮泵的参数，计算得到F＝9 826.845 N，齿轮轴材料选择42Cr，根据轴径得到轴截面惯性矩I＝30.68 mm4，最终计算得齿轮轴的挠度变形量为0.015 mm。

故齿轮轴变形后的径向间隙为：

将式（10）代入式（7）可变形为：

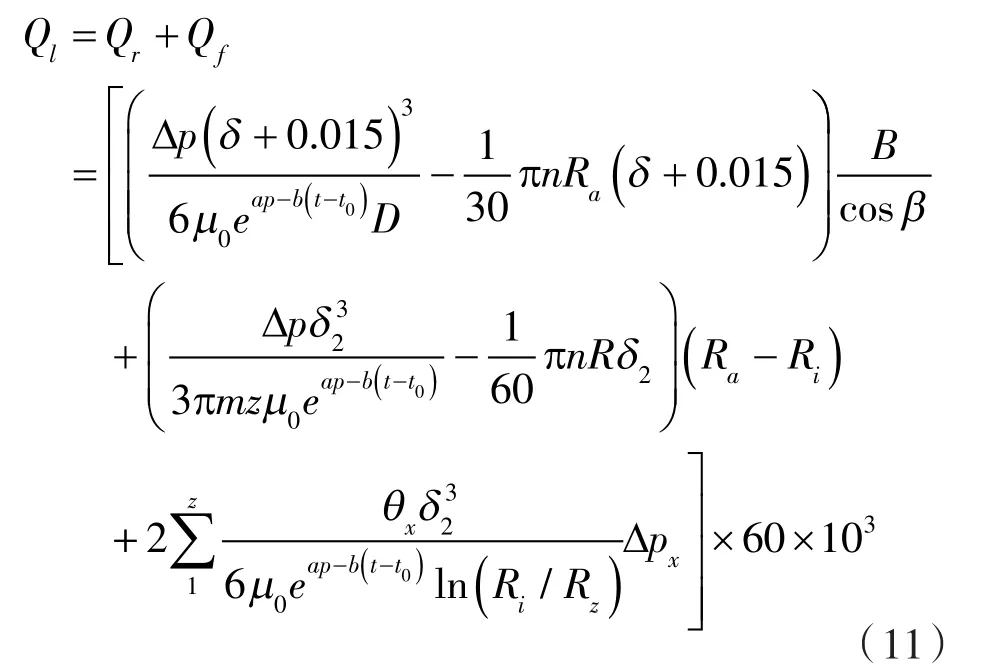
由式（11）可知在转速10 000 r/min条件下，代入为25，15及5 MPa，得到泄漏量分别为2.316 8，1.656，1.211 L/min，压力越大齿轮轴变形对泄漏量影响越大。

1.5 泵体变形对泄漏影响

齿轮泵在转动过程中，受到液压油产生的压力和由轴承所受的支撑反力的作用下，容易发生变形，泵体变形导致径向间隙δ 增大，进而影响径向泄漏，因此根据仿真结果考虑泵体变形重新建立径向泄漏模型。

2 最佳间隙的选取

由于径向间隙以及端面间隙的大小直接影响泵的整体性能，间隙较大，则泄漏增大，随之黏性摩擦损失将会减小，反之泄漏减小，黏性摩擦损失增大。为降低泵的功率损失，应设计出合理的径向间隙以及端面间隙，即为最佳间隙[10-13]。

2.1 径向最佳间隙

2.2 端面最佳间隙

3 圆弧齿轮泵的三维仿真

3.1 三维模型的建立

由前言中的齿轮泵参数，先利用Solid Works建立齿轮泵的三维模型，其中该模型的径向及端面最佳间隙根据最佳间隙的计算公式得到为0.007 mm及0.009 5 mm。然后利用SCDM建模软件抽取出齿轮泵内部流场三维模型。

3.2 边界条件设置和计算方法的确定

本文应用商业仿真软件ANSYS FLUENT进行流体仿真分析。FLUENT中Boundary Condition设置模型边界条件如图1所示。

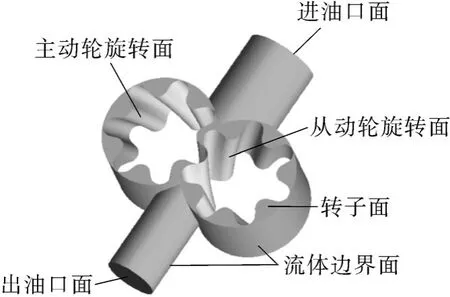
图1 流体模型边界设置Fig.1 Fluid model boundary setting

双圆弧斜齿轮泵进、出口边界设置为进口压强为大气压强，出口压强为25 MPa；流体边界采用无滑移边界条件；主、从动齿轮表面设为刚性（Ridig body）的旋转壁面边界；对于齿轮转动，选择动网格模型，本文选择弹性光顺法（Smoothing）和网格重构法（Remeshing）来进行动网格的演算。压力场计算一定步数基本稳定后，开启能量模型，同时开启 Viscous Model中的 Viscous Heating以激活能量方程和黏性加热计算，其他参数选择默认。

3.3 仿真结果分析

通过对负载进行参数化设置，仿真计算出不同工况下的流量情况，然后与考虑泄漏的理论流量进行比较，为验证建立的圆弧斜齿轮泵泄漏模型的正确性提供理论依据。

如图2所示为齿轮泵转速为10 000 r/min，出油口压力分别为5，15，25 MPa时的流量情况。由图2可得负载（出油口压力）越大，流量值越小，高压下的流量也受到压力的影响。在高转速下，压差越大，吸油口油液填充损失越大，从而导致出油口流量变化较大，故在中高压下，0.2～0.4旋转周期内流量脉动较大。

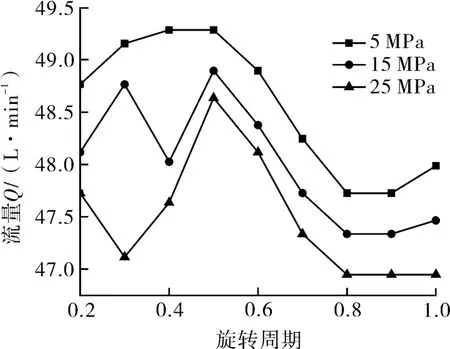
图2 不同负载下流量脉动Fig2 Flow pulsation under different loads

将圆弧齿轮泵相同转速下不同负载时一个旋转周期仿真流量平均值与理论流量值（根据理论流量公式与本文建立的齿轮泵总泄漏流量模型计算所得）进行比较，见表1。仿真流量值接近且略小于有泄漏理论流量，齿轮泵内部流场的仿真计算正确，同时也逆向证明了泄漏模型的正确性。

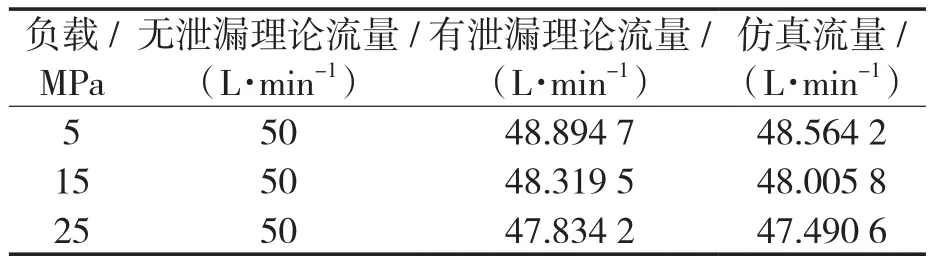
表1 不同负载下理论流量与仿真流量对比Tab.1 Comparison of theoretical flow rate and simulation flow rate under different loads

通过对齿轮泵内部流体的温度场仿真计算，发现除了两齿轮啮合处温升较大，其他区域温升不明显，监测齿轮泵出油口温度随旋转周期的变化情况如图3所示，齿轮泵内部流体温度在整个旋转过程中波动平稳，即流场油液黏度变化较小。

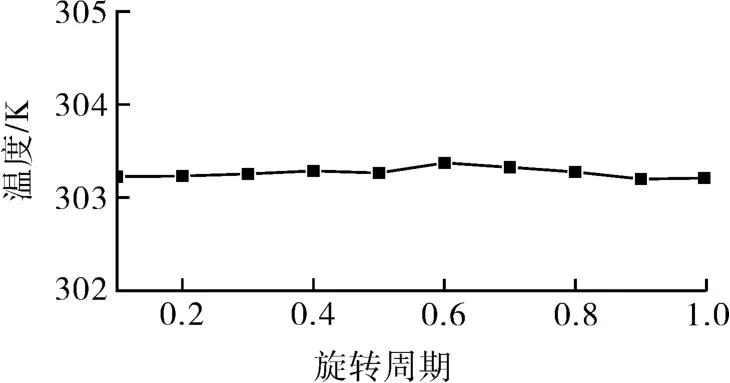
图3 出油口温度随旋转周期的变化Fig.3 Change of oil outlet temperature with rotational period

由第2节理论指导建立齿轮泵流体模型，对比根据传统间隙求解公式建立的齿轮泵流体模型，通过对两模型的分别仿真计算得到出油口流量如图4所示，考虑齿轮轴与泵体变形的出油口流量明显比未考虑变形的流量大，这也说明了齿轮轴和泵体变形对泄漏影响较大。

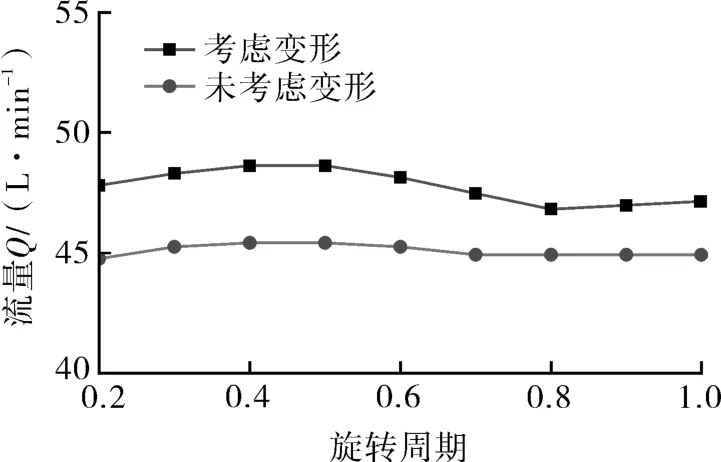
图4 变形对流量脉动影响Fig.4 Whether the influence of deformation on flow pulsation is considered

4 结论

（1）通过计算可得齿轮泵在25 MPa、10 000 r/min的工况下，其容积效率在95.5%～96%之间，符合高速高压圆弧斜齿轮泵的设计要求，这也为齿轮泵参数化设计提供理论依据和思路。

（2）在不同压力或转速下，理论流量（考虑泄漏）与仿真流量差值在0.214 3～0.343 6 L/min之间，证明了理论泄漏模型的正确性；

（3）齿轮泵出油口温度在整个旋转过程中波动不大，对流场油液黏度变化影响较小。

（4）考虑齿轮轴与泵体变形后，齿轮泵泄漏量明显减少。