不同除险加固方案下病险水库渗流特性研究 *

2022-04-26王正成毛海涛申纪伟

中国安全生产科学技术 2022年3期

王正成，孙岩，毛海涛，陈相，申纪伟

(1.重庆三峡学院土木工程学院，重庆 404100；2.山西农业大学城乡建设学院，山西晋中 030000)

0 引言

我国病险水库问题日益突出，根据《全国病险水库除险加固专项规划》统计表明，全国现有水库87 076 座，其中38 019 座为病险水库[1]，病险水库除险加固工作迫在眉睫。Yan等[2]提出1种病险水库综合评价技术，能确定水库的病害程度及加固方案。Huang等[3]提出了1种病险水库治理的预评价模型。Ma等[4]提出了1种适用于小型水库风险分析的模糊AHP评价方法。Xu等[5]开发了专门的SQL数据库，主要存储水库设计及施工资料、水库的功能、水库除险加固的信息。在评价方法方面，沈振中等[6]建立了能与实际情况吻合的水库除险加固效果量化评价模型。蒋清华等[7]研究了病险水库大坝风险全预警系统的架构，并将其概化为数据融合子系统、警兆辨识子系统、警源分析子系统和警情分析子系统。杨杰等[8]建立了基于区间数GRA决策和AHP-Entropy主客观综合赋权的病险水库除险加固方案的灰色关联度优选决策方法。胡江等[9]提出了溃坝生命损失的快速估算公式，建立了病险水库除险加固效应的定量评价模型。

在除险加固措施方面，林赛[10]提出非开挖顶管施工技术可有效阻断病险水库坝基的渗漏通道。袁明道等[11]探讨围井法在病险水库高压喷射灌浆工程中的应用效果。盛金保等[12]提出病险水库除险加固措施有压重、截水槽、复合土工膜、帷幕灌浆、防渗墙、岩溶灌浆、劈裂灌浆、下游导渗等。

当前研究成果主要集中在除险加固方案选择与效果评价、除险加固措施等方面，但关于不同除险加固方案对病险水库渗流场的影响方面的研究较少，尚缺乏系统的研究，需开展进一步的研究工作。本文以某病险水库为研究对象，借助有限元软件SEEP/W建立数值模型，计算得出渗流参量，针对病险水库的渗流特性展开分析，以期为病险水库除险加固方案的制定与选择提供理论支持。

1 土体渗流理论

大坝渗流示意图如图1所示，大坝渗流过程中[13]，整个坝体区域Ω内的渗流仅发生在自由面Гf以下区域Ωw中。A，D分别为上下游水位；BC为隔水边界；AE为渗流的自由面。自由面Гf并不确定，借助变分不等式方法转换达西定律。渗流速度如式(1)所示：

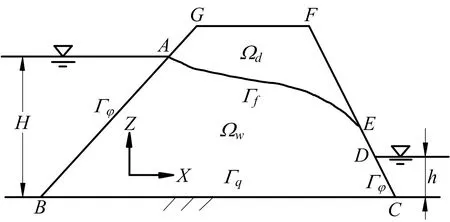
图1 大坝渗流示意Fig.1 Schematic diagram of dam seepage

v=-k∇φ+v0

(1)

式中：v为各个位置渗流速度，m·s-1；v0为初始渗流流速，m·s-1；k为二阶渗透张量；∇为梯度计算算子；φ=z+p/γw为总水头，m；z为垂直方向坐标值；p为岩土体内孔隙水压力，kPa；γw为渗透流体的容重，kN/m3。

初始渗流流速如式(2)所示：

v0=H(φ-z)k∇φ

(2)

式中：H(φ-z)为Heaviside函数，其表达式如式(3)所示：

(3)

整个大坝区域的渗流应满足连续性方程如式(4)所示：

∇·gv=0(Ω内)

(4)

且应满足定水头边界条件、流量边界条件、出逸面Signorini型互补边界条件、自由面边界条件。

(ψ-φk+1)TKφk+1≥(ψ-φk+1)Tqk

(5)

式(5)中各参数如式(6)～(10)：

K=∑εkε,kε∭ΩεBTkBdΩ

(6)

qk∑ε∭ΩεBTv0dΩ=Kεφk

(7)

(8)

(9)

(10)

式中：k为迭代步数；n为中节点数；B为整体几何矩阵；Hλ(φk-Z)为Heaviside自适应罚函数，目的在于解决自由面迭代过程中可能会出现的数值不稳定性及计算时出现的网格依赖性问题。当φk≥z+ξλ2，Hλ(φk-Z)=0；当φk≤z-ξλ1，Hλ(φk-Z)=1；当，z-ξλ1<φ≤z+ξλ2其表达式如式(11)所示：

(11)

式中：ξ为罚函数的自适应参量；其中λ1，λ2分别为单元内最低和最高积分点与最低和最高结点的垂直距离，m。

2 模型建立

2.1 工程概况

某堆石坝水库，最大坝高为34.5 m，坝顶高程为232.2 m，坝顶宽4.5 m，上游坝坡分别为(上→下)1∶1.8,1∶2.5,1∶2.5,1∶3，下游坝坡分别为(上→下)1∶2.25,1∶2.4,1∶1.65,1∶1.5。水库的水位及库容见表1，水库下游无积水。模拟过程中，上下游水位恒定，不考虑蓄水过程及上下游水位的波动。

表1 水库水位及库容Table 1 Water level and capacity of reservoir

坝基覆盖层厚0～38 m，为第4系人工填筑块石，呈现明显的层状结构，分为透水性存在一定差异的上下2层；覆盖层下方为元古界板溪群(Pt)砂质板岩，视为不透水层。

目前，该水库存在坝体填筑质量较差、坝体及坝基漏水严重、黏土斜墙达不到设计要求、基础清理不彻底等问题。基于《水库大坝安全评价导则》(SL258—2017)规定[14]，将该水库大坝定为三类坝，需进行除险加固处理。

2.2 计算参数

基于现场地质勘察资料和室内实验，确定各单元的渗透系数(见表2)。

表2 大坝渗透系数Table 2 Permeability coefficient of dam

2.3 建模剖面

选定某1不利地质剖面进行建模计算，加固前的水库计算剖面如图2(a)所示。结合该水库的实际险情，拟定3种除险加固方案。1)方案1：在大坝上游面，自坝顶232.2 m至死水位207.1 m铺设复合土工膜，根据SL/T231—1998《聚乙烯土工膜防渗工程技术规范》，再结合水库水头综合确定土工膜厚度为0.8 mm，如图2(b)所示。2)方案2：在大坝上游面207.6～221.6 m处进行修坡和平整，坡度为1∶2.5，从坝基沿坡面进行现浇0.3 m厚的混凝土面板，如图2(c)所示。3)方案3：沿坝顶向上游面采用黏土加宽至8 m，按1∶2.5坡度往上游放坡，计算剖面如图2(d)所示。3种除险加固方案的坝基均采用混凝土防渗墙控渗，防渗墙厚度为0.8 m。

图2 模型断面Fig.2 Model section map

此外，模拟中混凝土防渗墙深度S取0,5,10,15,20,25,30,35.8 m(全封闭式防渗墙)，共计8种。

2.4 数值模拟

首先开展建模前设置工作，包含分析设定、工具栏设定、工作区域设置、比例设置、绘图网格设置、坐标轴绘制，接着绘制模型，进一步将模型生成有限元区域，定义材料(黏土斜墙、堆石、上层坝基、下层坝基、复合土工膜、混凝土面板、混凝土防渗墙)并将材料赋予各有限元区域，划分网格并定义边界条件，检查模型并进行求解。

3 模拟结果及分析

当水库处于校核洪水位，采用方案2进行除险加固、防渗墙深度S=20 m时，大坝渗流等势线分布情况如图3所示。可见混凝土面板和防渗墙消杀水头作用效果显著，渗流等势线集中在2板块中。

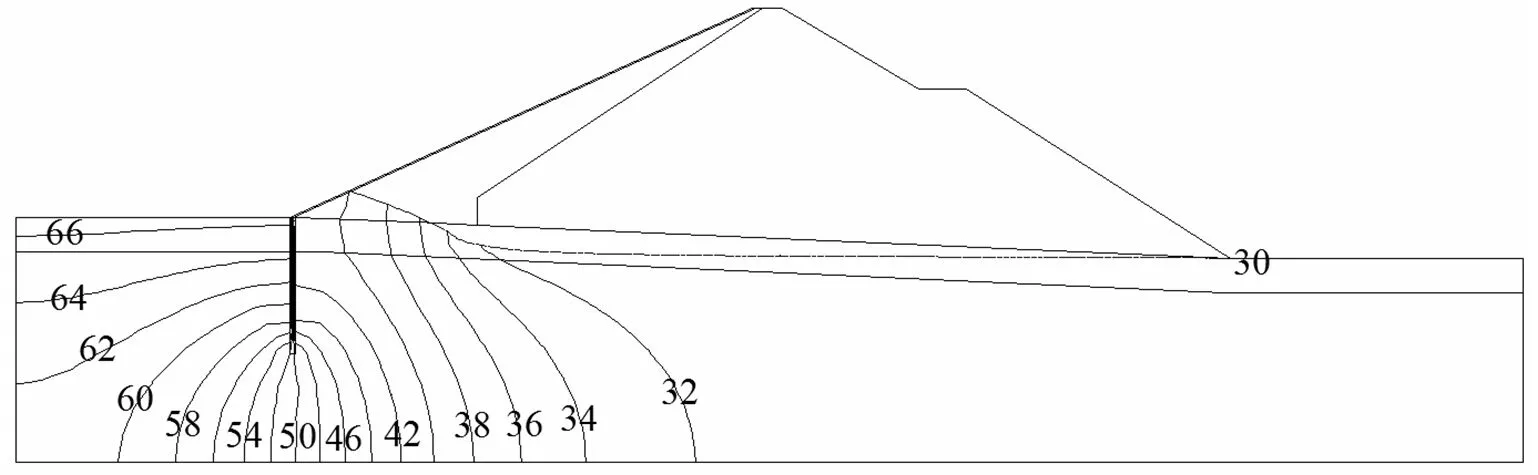
图3 大坝渗流等势线Fig.3 Seepage equipotential lines of dam

3.1 大坝渗流特性分析(未除险加固)

未除险加固时，作4种水位下渗流量Q、出逸坡降J1、出逸流速v1变化图，如图4～6所示。

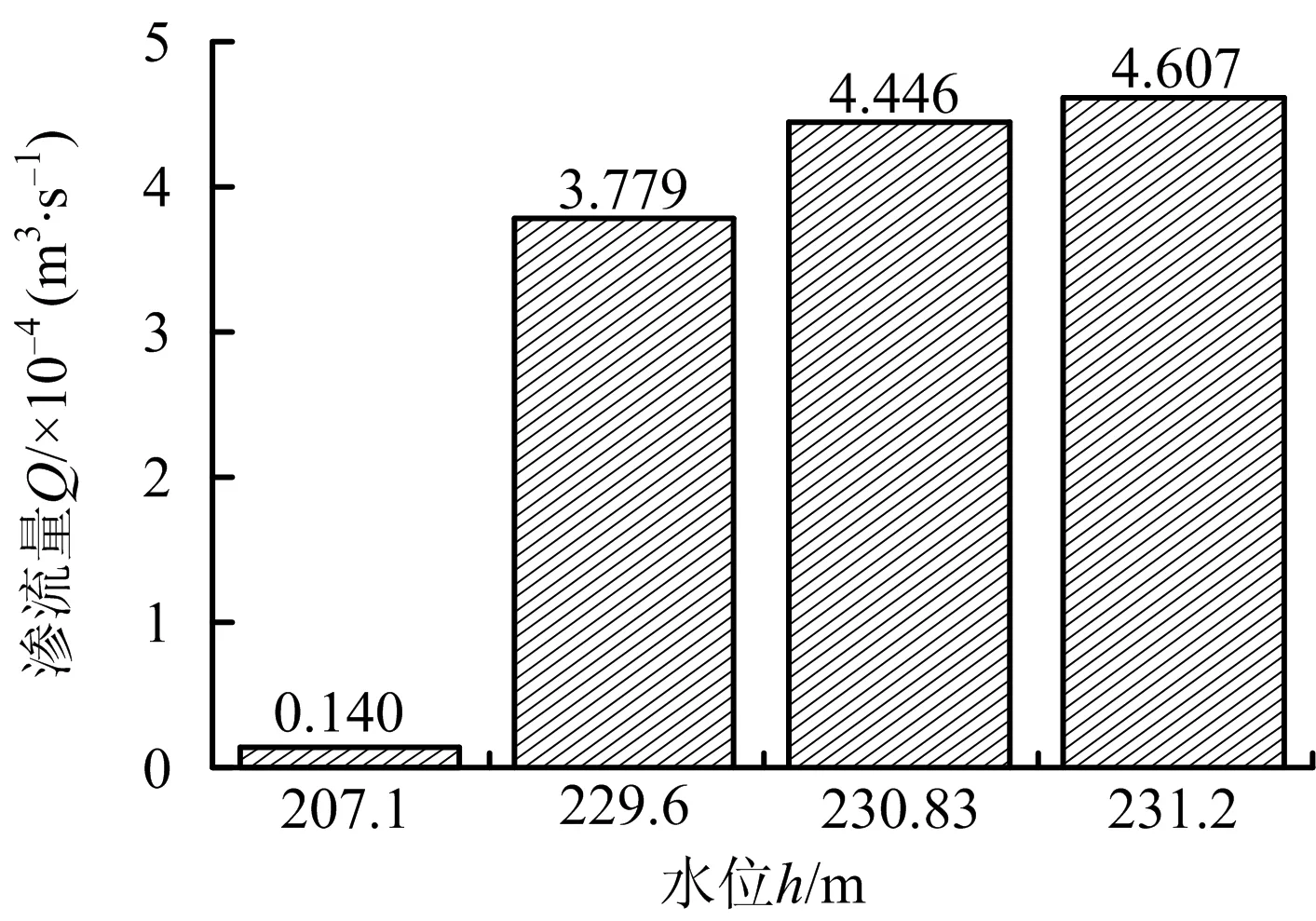
图4 渗流量变化(未除险加固)Fig.4 Change graph of seepage dischargequantity (unreinforced)

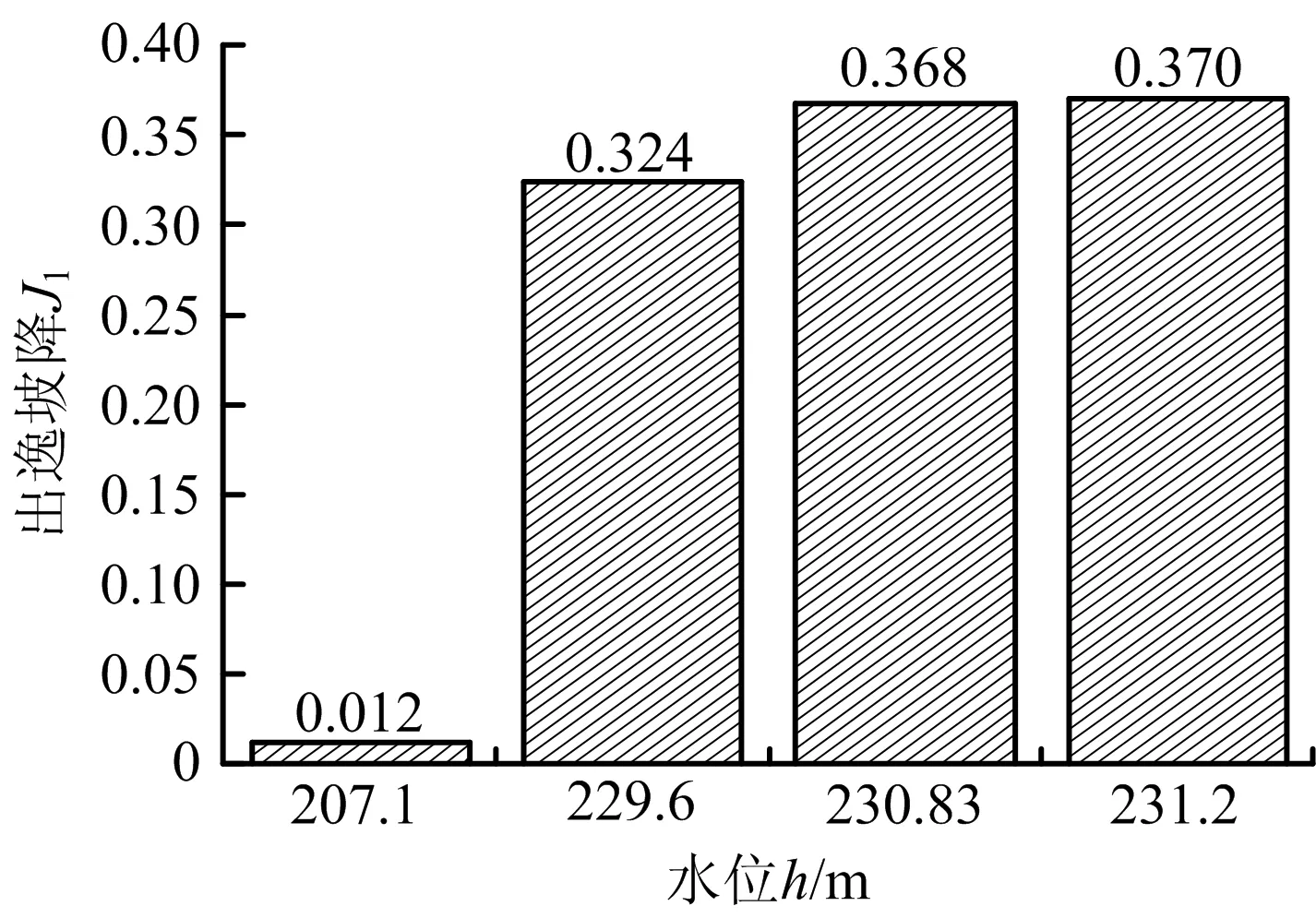
图5 出逸坡降变化(未除险加固)Fig.5 Change graph of outflow gradient (unreinforced)

由图4不难得出，随着库水位升高，大坝渗流量逐渐增大。当库水位由死水位升高至校核洪水位时，渗流量由1.4×10-5m3/s增大至4.607×10-4m3/s，增大3 190.71%。同理由死水位升高至正常蓄水位和设计洪水位时，渗流量增大2 599.29%,3 075.71%。

同理可得，当库水位由死水位升高至正常蓄水位、设计洪水位、校核洪水位时，出逸坡降J1增大2 600%,2 966.67%,3 075.71%。

由图6可得，当库水位由死水位升高至正常蓄水位、设计洪水位、校核洪水位时，出逸流速v1增大2 474.23%,2 825.77%,2 845.36%。

图6 出逸流速变化(未除险加固)Fig.6 Change graph of outflow velocity (unreinforced)

3.2 大坝渗流特性分析(方案1)

基于方案1对大坝进行除险加固，坝体和坝基分别采用复合土工膜、垂直防渗墙进行除险加固；渗流量Q随防渗墙深度S的变化曲线如图7所示。

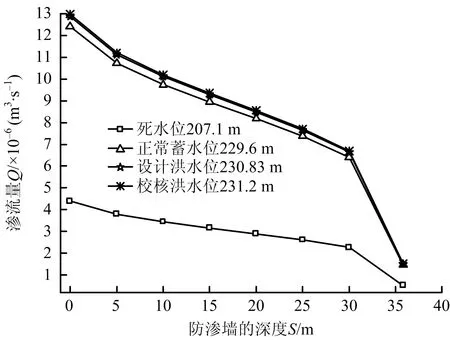
图7 渗流量Q随防渗墙深度S的变化曲线(方案1)Fig.7 Change curves of seepage quantity Q with depth of cutoff wall S (scheme 1)

由图7不难得出，各曲线变化规律类似；渗流量Q随着防渗墙深度S的增大而减小，且当防渗墙深度由30 m增大至35.8 m时，渗流量降低速率增大显著。以库水位h=207.1 m为例进行阐述，曲线总体呈降低趋势，当防渗墙深度由0 m增大至35.8 m时，渗流量从4.386×10-6m3/s降低至5.16×10-7m3/s，降幅为88.24%；当防渗墙深度S由30 m增大至35.8 m时，渗流量降低77.19%。同理，防渗墙深度由0 m增大至35.8 m时，库水位h=229.6，230.83，231.2 m对应的渗流量分别降低88.22%，88.21%，88.21%。

各水位下大坝出逸坡降J1变化曲线如图8所示。

图8 出逸坡降J1随防渗墙深度S的变化曲线(方案1)Fig.8 Change curves of outflow gradient J1 with depth of cutoff wall S (scheme 1)

对比图7和图8不难发现，2图中曲线的变化规律类似，都是随着防渗墙深度S的增大而降低。防渗墙深度S由0 m增大至35.8 m时，库水位h=207.1，229.6，230.83，231.2 m对应的出逸坡降分别降低87.98%，87.86%，87.93%，88.05%。

作各水位下大坝出逸流速v1变化曲线如图9所示。

图9 出逸流速v随防渗墙深度S的变化曲线(方案1)Fig.9 Change curves of outflow velocity v with depth of cutoff wall S (scheme 1)

根据达西定律可知，渗流速度可由渗透坡降和材料渗透系数推求得出，渗流速度与渗透坡降呈正比关系；因此，图9和图8中曲线变化规律类似，都是随着防渗墙深度S的增大而降低；且当防渗墙转化为全封闭式防渗墙时，出逸流速降低速度明显增大。当S由0 m增大至35.8 m时，出逸流速(h由低到高)分别降低64.77%，88.15%，83.91%,88.15%。

进一步作防渗墙底部渗透坡降J2的变化曲线如图10所示。

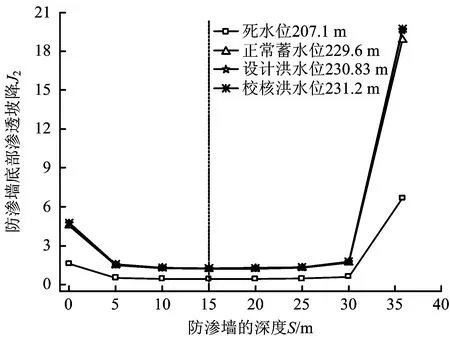
图10 防渗墙底部渗透坡降J2随防渗墙深度S的变化曲线(方案1)Fig.10 Change curves of seepage gradient at bottom of cutoff wall J2 with depth of cutoff wall S (scheme 1)

分析图10可得，各曲线变化规律类似，防渗墙底部渗透坡降J2以S=15 m为分界线，左侧呈减小趋势，右侧呈增大趋势；此外，曲线在首尾2端变化显著，中间区域趋于稳定。

以库水位h=207.1 m为例进行阐述分析，当防渗墙深度S由0 m增大至15 m时，防渗墙底部渗透坡降J2从1.612降低至0.429，降幅为73.39%；当防渗墙深度S由15 m增大至35.8 m时，防渗墙底部渗透坡降J2从0.429增大至6.668，增幅为1 454.31%；当S由0 m增大至5 m，J2降低66.94%；S由5 m增大至30 m，J2增大12.76%；S由30 m增大至35.8 m，J2增大1 009.48%。

当S由0 m增大至15 m时，J2(h=229.6，230.83，231.2 m)皆降低73.38%；S由15 m增大至35.8 m时，J2分别增大1 453.54%，1 454.33%，1 453.54%。

3.3 大坝渗流特性分析(方案2)

基于方案2对大坝进行除险加固，坝体和坝基分别采用混凝土面板、垂直防渗墙进行防渗。渗流量Q、出逸坡降J1、出逸流速v1、防渗墙底部渗透坡降J2变化曲线如图11～14所示。

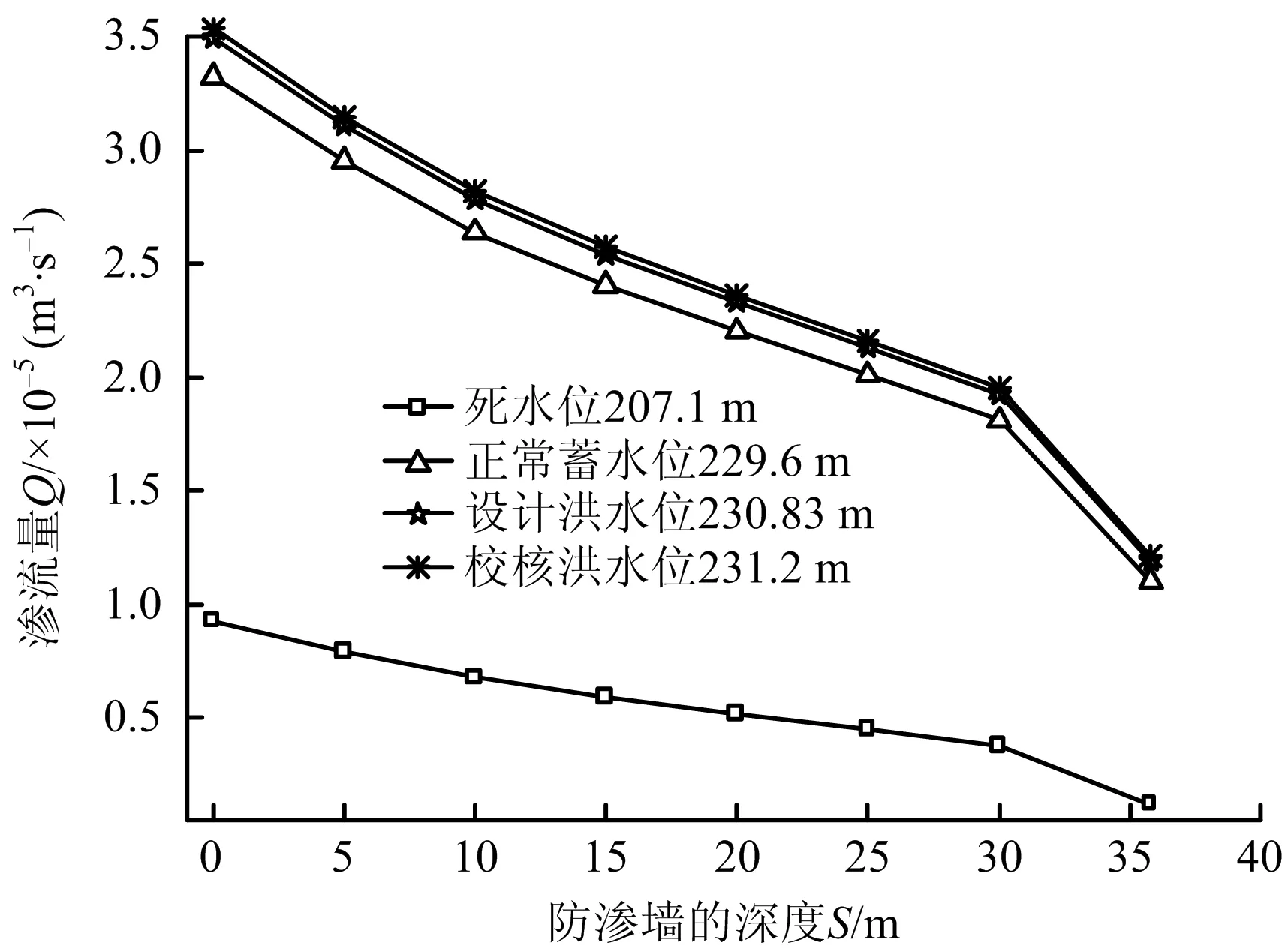
图11 渗流量Q随防渗墙深度S的变化曲线(方案2)Fig.11 Change curves of seepage quantity Q with depth of cutoff wall S (scheme 2)

图12 出逸坡降J1随防渗墙深度S的变化曲线(方案2)Fig.12 Change curves of outflow gradient J1 with depth of cutoff wall S (scheme 2)

图13 出逸流速v随防渗墙深度S的变化曲线(方案2)Fig.13 Change curves of outflow velocity v with depth of cutoff wall S (scheme 2)

对比图11～13可知，图中各曲线变化规律类似，都随着防渗墙深度S的增大而降低，且当防渗墙深度S由30 m增大至35.8 m时，降低速率明显增大。①当防渗墙深度S由0 m增大至35.8 m时，渗流量Q(h由低到高)分别降低86.88%，66.77%，65.87%,65.68%；出逸坡降J1(h由低到高)分别降低86.9%，66.92%，66.06%，65.83%；出逸流速v1(h由低到高)分别降低86.87%，67.75%，66.92%，66.71%。②当防渗墙深度S由30 m增大至35.8 m时，渗流量Q、出逸坡降J1、出逸流速v1分别降低37.83%～67.67%，38.03～67.79%，39.43～68.06%。

对比图10和图14，2图中曲线变化规律类似，以防渗墙深度S=25 m为分界线，防渗墙底部渗透坡降J2随着防渗墙深度S的增加先降低后增大；此外，曲线在首尾2端变化速率快，中间区域(10 m≤S≤30 m)趋于稳定。

图14 防渗墙底部渗透坡降J2随防渗墙深度S的变化曲线(方案2)Fig.14 Change curves of seepage gradient at bottom of cutoff wall J2 with depth of cutoff wall S (scheme 2)

当S由5 m增大至25 m时，防渗墙底部渗透坡降J2(h由低到高)分别降低75.36%，75.25%，75.26%，75.25%；当S由25 m增大至35.8 m时，防渗墙底部渗透坡降J2(h由低到高)分别增大895.11%，895.58%，895.79%，895.63%。

3.4 大坝渗流特性分析(方案3)

当坝体和坝基分别采用黏土斜墙、垂直防渗墙进行除险加固时。作渗流量Q、出逸坡降J1、出逸流速v1、防渗墙底部渗透坡降J2变化曲线如图15～18所示。

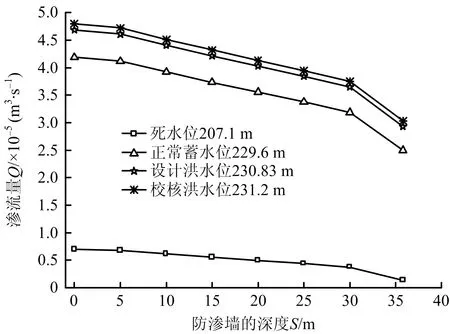
图15 渗流量Q随防渗墙深度S的变化曲线(方案3)Fig.15 Change curves of seepage quantity Q with depth of cutoff wall S (scheme 3)

图16 出逸坡降J1随防渗墙深度S的变化曲线(方案3)Fig.16 Change curves of outflow gradient J1 with depth of cutoff wall S (scheme 3)

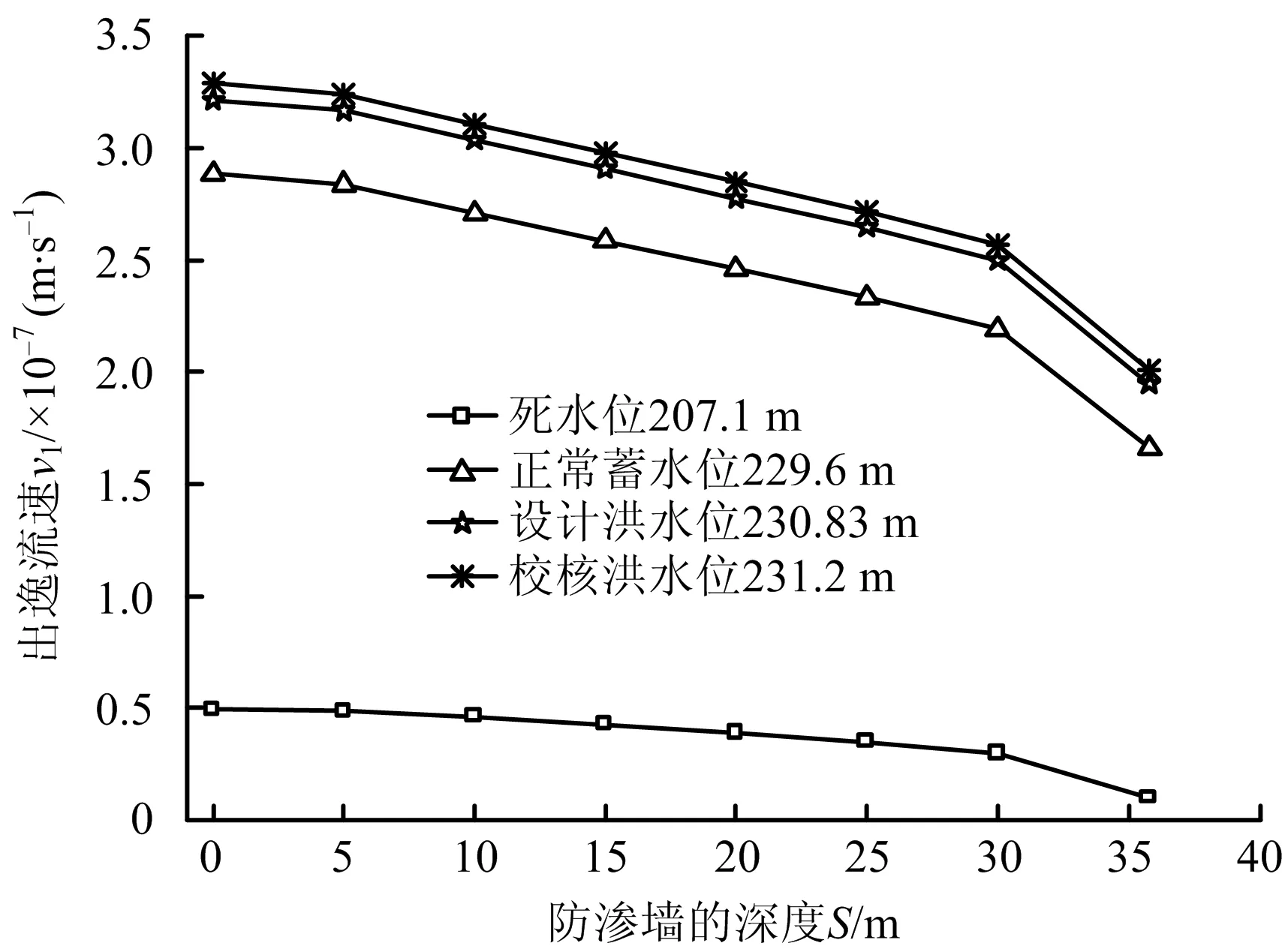
图17 出逸流速v随防渗墙深度S的变化曲线(方案3)Fig.17 Change curves of outflow velocity v with depth of cutoff wall S (scheme 3)

分析图15～17不难得出，3个图中各曲线变化规律类似，都随着防渗墙深度的增大而降低，且在最后阶段(防渗墙深度S由30 m增大至35.8 m)变化显著。

1)当防渗墙深度S由0 m增大至35.8 m时，渗流量Q(h由低到高)分别降低80.38%，40.41%，37.43%，36.84%；出逸坡降J1(h由低到高)分别降低80.49%，40.68%，37.67%，37.14%；出逸流速v(h由低到高)分别降低80.72%，42.44%，39.42%，38.86%。2)在最后阶段，当防渗墙深度S由30 m增大至35.8 m时，渗流量Q、出逸坡降J1、v分别降低19.21%～63.23%，19.58%～63.64%，21.66%～67.84%。

由图18不难得出，以S=20 m为分界线，防渗墙底部渗透坡降J2先降低后增大，在最后阶段(S由30 m增大至35.8 m)快速增大。以死水位为例进行阐述说明，当S由5 m增大至20 m时，防渗墙底部渗透坡降J2由0.678降低为0.633，降幅为6.64%；当S由20 m增大至30 m时，防渗墙底部渗透坡降J2由0.633增大至6.7，增大958.45%；当S由30 m增大至35.8 m时，防渗墙底部渗透坡降J2由0.793增大至6.7，增大744.89%。

当S由5 m增大至20 m时，J2(h=229.6，230.83，231.2 m)分别降低10.7%，10.7%，10.66%；当S由20 m增大至30 m时，J2(h=229.6，230.83，231.2 m)分别增大938.34%，938.72%，938.4%；当S由30 m增大至35.8 m时，J2(h=229.6，230.83，231.2 m)分别增大739.74%，739.99%，740.01%。

4 控渗效果对比分析

为探明3种除险加固方案的控渗效果，针对加固前后的渗流参数进行对比分析。3种方案的防渗墙深度S=15 m，此时防渗墙截断上层坝基，并嵌入下层坝基一定深度，防渗效果相对较好。作Q，J1，v1，J2对比图(见图19～22)。

图19 渗流量Q对比Fig.19 Comparison chart of seepage quantity Q

分析图19可得，除险加固后渗流量Q显著降低。以正常蓄水位为例进行阐述分析，加固前、采用方案1～3加固后渗流量Q分别为3.779×10-4，8.949×10-6，2.406×10-5，3.734×10-5m3/s，加固后(方案1～3)渗流量Q分别降低97.9%，93.9%，90.38%；水库处于死水位时，渗流量Q(采用方案1～3加固)分别降低77.41%，57.64%，60.34%；在设计洪水位时，渗流量Q(采用方案1～3加固)分别降低97.91%，94.28%，90.51%；在校核洪水位时，渗流量Q(采用方案1～3加固)分别降低97.97%，94.41%，90.62%。

由此可见，3种除险加固方案均能有效降低渗流量Q；且降低渗流量Q的效果由好到差排序为：方案1、方案2、方案3。

由图20可得，当h=207.1 m时，采用方案1加固后J1增大591.67%，采用方案2、3加固后J1分别降低57.17%，59.66%；当h=229.6 m时，加固后(方案1～3)J1分别降低27.47%，93.58%，99%；当h=230.83 m时，加固后(方案1～3)J1分别降低33.7%，94.04%，99.01%；当h=231.2 m时，加固后(方案1～3)J1分别降低33.51%，93.99%，98.99%。

图20 出逸坡降J1对比Fig.20 Comparison chart of outflow gradient J1

不难得出，各除险加固方案能有效控制出逸坡降J1；且控制出逸坡降J1效果由好到差排序为：方案3、方案2、方案1。

在分析出逸坡降J1的基础上进一步分析出逸流速v。对比图21和图20可知，2图的变化规律类似，不做详细赘述。各方案均可有效降低出逸流速v1，且方案2效果最佳，方案3其次，方案1的效果相对较差。

图21 出逸流速v对比Fig.21 Comparison chart of outflow velocity v

进一步分析防渗墙底部渗透坡降的变化规律。由于加固前无垂直防渗墙，在分析防渗墙底部渗透坡降的变化规律时，只对比分析采用3种除险加固方案后的防渗墙底部渗透坡降J2。以正常蓄水位(h=229.6 m)为例进行分析，采用方案1～3方案加固后，防渗墙底部渗透坡降J2分别为1.214，2.075，1.872。各水位下防渗墙底部渗透坡降J2由小到大排序为：方案1、方案3、方案2。

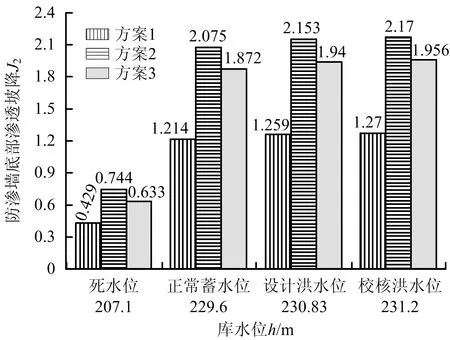
图22 防渗墙底部渗透坡降对比Fig.22 Comparison chart of seepage gradient at bottom of cutoff wall

5 讨论

5.1 防渗墙底部渗透坡降变化规律原因分析

分析防渗墙底部渗透坡降J2变化规律的原因如下：

1)当防渗墙深度S=0 m时，防渗墙底部渗透坡降J2较大(1.612～4.77)；坝基未采用控渗措施，坝体采用复合土工膜防渗，此时最有利于渗水的通道为上层坝基，大量渗水通过防渗墙底部，导致出现较大的渗透坡降值。

2)当防渗墙深度S=5～30 m时，防渗墙底部渗透坡降J2趋于稳定；当防渗墙底端嵌入坝基，加之坝基渗透系数较小(为弱透水层)，防渗墙与坝基形成半封闭式联合防渗体系，控渗效果显著；因此，此阶段防渗墙底部渗透坡降J2趋于稳定，波动幅度较小。

3)当防渗墙深度S=35.8 m时，防渗墙底部渗透坡降J2出现极大值(6.668～19.73)；针对这个现象，运用水力学中的局部水头损失进行解释，当防渗墙底部刚接触基岩(砂质板岩)时，墙下开口尺寸小，水的流速大，局部损失就很大，这部分水头损失就叠加到防渗墙底部的水头差上，渗透坡降出现极大值。

5.2 除险加固方案选择

基于上述分析可知，采用上述方案加固后，渗流量均较小(3.162×10-6～4.32×10-5m3/s)，能满足水库蓄水要求。此外，除险加固后出逸坡降(0.004 84～2.977)、出逸流速(4.016×10-8～7.308×10-7m/s)均较低，土体不会发生渗透破坏。但除险加固后，防渗墙底部渗透坡降较大(0.429～2.17)，设计及施工中应重点考虑，防止发生渗透破坏。

因此，从渗流场角度考虑，3种除险加固方案均能满足要求，能有效降低病险水库的渗流量、出逸坡降、出逸流速。但在选择最佳方案时，应结合各方案的特点、施工周期、施工难易程度、工程成本、应力特征等方面综合确定。