考虑数据去噪分解的滑坡位移组合预测研究*

2022-04-26庞旭卿

中国安全生产科学技术 2022年3期

方筠，庞旭卿,2

(1.陕西铁路工程职业技术学院，陕西渭南 714000；2.西安理工大学土建学院，陕西西安 710048)

0 引言

近年，我国水利建设快速发展，库区工程日益增加，带来巨大经济效益的同时，诱发大量库岸滑坡。因此，为切实保证库区工程安全运营，开展库岸滑坡研究具有重要意义[1-3]。滑坡位移预测可有效掌握滑坡变形发展规律，是其稳定性评价的直观证据。在滑坡位移预测研究中，王兴科等[4]、拉换才让等[5]得出组合预测相较传统单项预测具有更好的预测精度和稳定性。受监测环境影响，滑坡位移数据含有一定的误差信息[6]，将对预测结果产生直接影响。因此，在构建位移预测模型之前，需先进行滑坡位移数据去噪分解处理。廖康等[7]、李骅锦等[8]研究得出极限学习机在滑坡位移预测中具有较好的适用性；李炯等[9]验证Arima模型对滑坡位移预测误差的修正能力。综上，说明利用极限学习机和Arima模型构建滑坡位移组合预测模型是可行的。本文以滑坡位移监测结果为基础，在位移数据去噪分解基础上，利用极限学习机和Arima模型分别实现滑坡位移趋势项预测和误差修正预测，以达到滑坡位移组合预测的目的，以期掌握滑坡位移变形规律，研究结果可为其灾害防治提供理论指导。

1 基本原理

首先，对滑坡位移数据进行去噪分解处理，即将滑坡位移数据分解为趋势项和误差项；其次，以极限学习机(Extreme Learning Machine,ELM)为理论基础，通过递进优化处理保证模型参数最优性，并构建趋势项预测模型；最后，将趋势项预测误差与数据分解误差项叠加，组成新的误差序列，利用Arima模型实现误差修正，将误差修正预测结果与趋势项预测结果叠加，综合实现滑坡位移的组合预测。

1.1 数据去噪分解模型构建

据文献[6]可知，受监测环境及人为等因素影响，滑坡变形数据往往含有一定误差信息，即滑坡位移数据可划分为趋势项和误差项，如式(1)所示：

Yt=γt+εt

(1)

式中：Yt为滑坡位移值；γt为趋势项；εt为误差项。

小波去噪能有效分解滑坡位移数据趋势项和误差项，但传统小波无法处理滑坡位移数据的相位信息，Morlet复小波法可有效解决上述问题。Morlet复小波法属连续小波，包括实部和虚部2部分，前者属偶函数，后者属奇函数，不仅能有效解决滑坡位移数据的幅频特性和相位信息，还可以解决奇异点问题。因此，利用Morlet复小波分解滑坡位移数据的趋势项和误差项是可行的。基于Morlet复小波基本原理，ψt表达式如式(2)所示：

ψt=(πfb)0.5exp(2jπfct)exp(-t2/fb)

(2)

式中：fb为宽带参数；fc为中心频率参数；j为衰减参数。

在Morlet复小波去噪过程中，小波分解层数、阈值选取标准对其分解效果具有直接影响，为保证分解效果，需要对其结构参数进行优化处理。考虑粒子群算法(Particle Swarm Optimization,PSO)具有较强的全局寻优能力，可实现小波分解层数和阈值选取标准的优化处理。优化过程主要包括以下3个步骤：

1)参数初始化。对粒子群参数进行初始化设置，如规模设定为500，粒子维数设定为2，分别代表小波分解层数和阈值选取标准，最大迭代次数设定为500次，其余参数随机设置。

2)迭代寻优。以预测误差为适宜度函数，首先对所有粒子的适宜度值进行计算，并确定最优者作为全局适宜度值；其次，对粒子进行迭代寻优，每迭代1次，则计算1次粒子的适宜度值，并将粒子适宜度值与全局适宜度值对比，若前者更优，则将其替代全局适宜度值；反之，继续寻优，直至满足期望或达到最大迭代次数。

3)参数输出。当寻优结束后，把小波分解层数和阈值选取标准输出，作为Morlet复小波的对应参数，以完成寻优处理。

数据去噪分解效果的评价指标主要为信噪比和平滑度指标，2者评价内容存在一定差异，为实现分解效果的全面评价，提出利用2者归一化值构建滑坡位移数据信息分解处理效果的综合评价指标p，如式(3)所示：

p=gx+gp

(3)

式中：gx和gp分别为信噪比及平滑度指标的归一化值。

据p值大小可判断信息分解效果的优劣，判据为：p值越大，信息分解效果越优；反之，信息分解效果越差。

1.2 趋势项预测模型的构建

极限学习机是1种新型神经网络，一般具有3层拓扑结构，包括输入层、隐层和输出层，具有较强的非线性预测能力。结合ELM模型基本原理，其预测过程如式(4)所示：

(4)

式中：yj为预测值；L为隐层神经元个数；g(x)为激励函数；βi、wi为连接权值；xj为输入层；bi为阈值。

ELM模型对噪声敏感，易造成映射过程的随机性，如核函数存在一定随机性，将影响预测结果。Huang[10]将正则化系数引入ELM模型，构建KELM模型，降低噪声和随机映射对预测精度的影响，不过KELM模型亦属单核结构，为避免核函数的敏感性影响，MKELM模型将全局核和局部核融合，有效增强了模型的泛化能力。因此，确定趋势项的预测模型为MKELM模型。

在MKELM模型应用过程中，隐层节点数和连接权值具较强的随机性，对预测结果具有一定影响。为切实保证预测效果，需对上述2参数进行优化处理，具体优化处理包括以下2部分：

1)隐层节点数优化。在传统神经网络的预测过程中，多利用经验公式确定隐层节点数，如式(5)所示：

(5)

式中：m，n分别为输入、输出层的节点数。

通过式(5)得到隐层节点数经验值为16，为实现其优化处理，将隐层节点数的取值范围设定为12～20间的偶数值，通过对所有隐层节点数的预测试算，确定预测效果最优者即为MKELM模型的隐层节点数。

2)连接权值优化。由于连接权值具区域取值特征，不能通过上述试算进行优化处理，且由于布谷鸟算法(Cuckoo Search，CS)具较强的寻优能力，是1种新型启发式算法，利用其实现连接权值的优化处理可行。据文献[11]可知，CS算法存在搜索能力相对偏弱、易陷入局部极值等不足，可通过ICS算法解决该问题。采用ICS算法对连接权值进行优化处理，优化流程如图1所示。

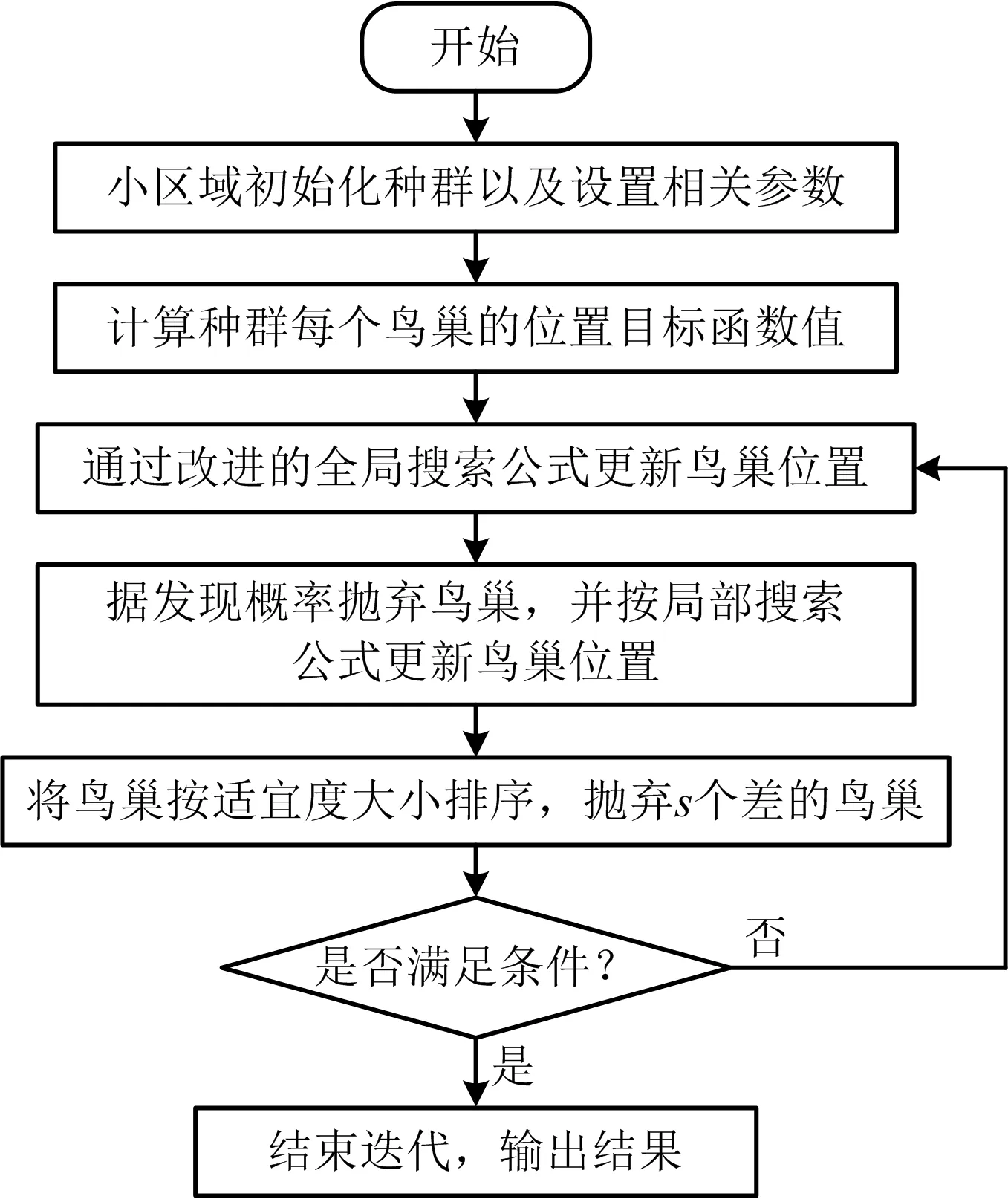
图1 ICS算法优化流程Fig.1 Optimization process of ICS algorithm

通过上述递进优化处理，可有效保证趋势项预测模型的预测效果，但限于滑坡变形的非线性特征，预测结果亦会存在一定预测误差，进行误差修正预测十分必要。

1.3 误差修正预测模型构建

基于趋势项预测，将其预测误差与数据分解的误差项叠加，组成新的误差序列。利用Arima模型构建误差序列的修正模型。修正过程如式(6)所示：

(6)

式中：zt为修正预测值；t为序列节点编号；m和j为常数；φm为自回归系数；p为自回归阶次；θj为滑动系数；q为滑动平均阶次；at为白噪声。

最后，将趋势项预测结果和误差修正预测结果叠加，作为滑坡位移的最终预测值。

2 实例分析

2.1 工程概况

枯木滑坡隶属鲁地拉水电站库区，平面具圈椅状，前缘高程约1 170 m，后缘高程约1 365～1 380 m，高差约210 m，纵向长度约430 m，宽度约400 m，厚度间于20～30 m，体积约324万m3，属大型滑坡[11]。在地质构造方面，程海-宾川断裂的分支构造从滑坡后缘通过，对滑坡形成影响较大；同时，据现场钻探，区内基岩以侏罗系页岩为主，局部夹杂石英砂岩，上覆第四系以崩坡积为主。

由于库区蓄水及区内工程建设，枯木滑坡变形日益明显，为准确掌握其变形特征，对其进行变形监测。其中，TP01监测点位于滑坡左前缘，TP12监测点位于滑坡右后缘，2者监测结果较为完善，可用以进行滑坡位移组合预测研究。

监测过程中，由2013年7月26日至2016年8月9日，共计1 110 d，监测周期为15 d，共得到75个周期的位移监测结果，位移曲线如图2所示。据图2，TP01监测点的最终变形量为47.70 mm，TP12监测点的最终变形量为193.90 mm；其中，TP12监测点的变形曲线具有2次位移突变特征，第1次由25 mm突变至75 mm，第2次从75 mm突变至175 mm，结合现场监测过程，2次突变变形是因TP12监测点附近发生了2次小规模滑动，但总体来说滑坡未出现整体滑动。

图2 滑坡位移-时间曲线Fig.2 Curves of landslide displacement with time

2.2 滑坡位移组合预测分析

在预测过程中，为充分验证预测思路的普适性及滚动预测能力，且考虑到滑坡位移数据的监测时间较长，将预测过程划分为2阶段：1)中期预测，训练样本为1～40周期，41～45为验证样本。2)后期预测，训练样本为1～70周期，71～75周期为验证样本，并外推预测4个周期。

1)中期预测结果分析

为充分评价不同去噪分解阶段和优化阶段的预测效果，以TP01监测点中期为例，进行详述分析。

①数据去噪分解效果分析。为验证Morlet复小波在滑坡位移数据信息分解处理中的适用性，将其分解结果与若干小波去噪和Kalman滤波的处理结果进行对比统计，见表1。由表1可知，3类去噪模型的分解结果存在明显差异，其中，Morlet复小波的评价指标p值为1.718，相对最大，说明其分解效果相对最优；其次是Kalman滤波和db小波。因此，在滑坡数据去噪分解方面，Morlet复小波更适用于滑坡位移数据的去噪分解处理。

表1 不同去噪模型的分解结果Table 1 Decomposition results of different denoising models

利用PSO算法对Morlet复小波进行优化处理，得到优化处理前后结果见表2。由表2可知，PSO-Morlet复小波较Morlet复小波的基础指标gx和gp值均有不同程度的提高，致使评价指标p值增加，即经PSO算法的优化处理，Morlet复小波的分解效果得以明显提高，验证PSO算法的有效性。

表2 Morlet复小波优化前后的分解结果Table 2 Decomposition results of Morlet complex wavelet before and after optimization

综上，Morlet复小波适用于滑坡位移数据的信息分解处理，经PSO算法优化处理，能进一步提高其分解效果。因此，采用PSO-Morlet复小波实现滑坡位移数据趋势项和误差项的分解处理是合理有效的。

②趋势项优化预测分析。按照趋势项的递进优化处理步骤，先对ELM模型的隐层节点数进行优化筛选，结果见表3。由表3可知，不同隐层节点数条件下的平均相对误差值存在一定差异，侧面验证进行隐层节点数优化筛选的必要性；同时，随隐层节点数增加，预测结果的平均相对误差值呈先减小后增加趋势，且在隐层节点数为18时，具有相对最小的平均相对误差值，进而确定MKELM模型的隐层节点数为18。

表3 隐层节点数的优化筛选结果Table 3 Optimization screening results of hidden layer node number

依次优化ELM模型的核函数，并得到3类核函数优化模型的预测结果，见表4。据表4，随核函数的递进优化处理，在相应验证节点处的相对误差值均呈不同程度的减小，其中，MKELM模型预测结果的相对误差间于2.38%～2.71%，平均相对误差为2.55%，预测效果相对最优，但预测精度一般，侧面说明后续递进优化预测和误差修正预测的必要性。

表4 不同核函数优化模型的预测结果Table 4 Prediction results of different kernel function optimization models

在前述优化处理基础上，对MKELM模型的连接权值进行优化处理，并对CS算法和ICS算法的预测结果均进行统计，见表5。由表5可知，在相应验证节点处，ICS-MKELM模型的相对误差值均相对较小，且其平均相对误差为2.18%，优于CS-MKELM模型和MKELM模型，说明ICS算法能有效优化MKELM模型的模型参数，达到提高预测精度的目的，较CS算法具有显著的优越性，验证ICS算法的有效性。

表5 连接权值优化处理后的预测结果Table 5 Prediction results of optimized connection weights

为进一步对比CS算法和ICS算法的优化效果，对2者的特征参数进行统计，见表6。据表6，ICS算法较CS算法具有相对更短的训练时间和更少的迭代次数，说明前者具有更快的收敛速度；同时，ICS算法具有相对更多的局部优化次数，说明其较CS算法具有更强的全局优化能力。因此，ICS算法较CS算法具有明显的优越性，适用于MKELM模型的参数优化。

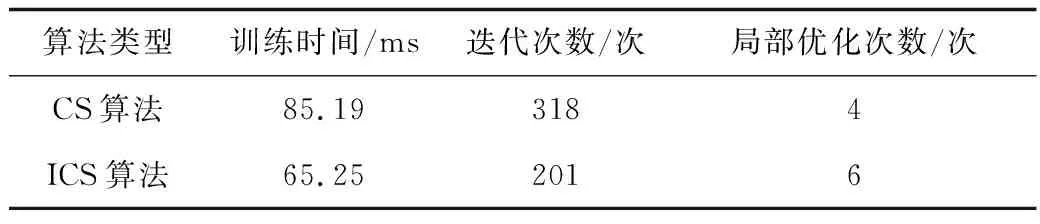
表6 CS算法和ICS算法优化过程的特征参数Table 6 Characteristic parameters of CS algorithm and ICS algorithm optimization process

为进一步总结趋势项递进优化处理的预测效果，先对不同阶段的预测模型进行命名。其中，模型1：ELM模型，其主要实现隐层节点数优化处理；模型2：KELM模型，其主要是在ELM模型基础上进行核函数优化；模型3：MKELM模型，其主要是在KELM模型基础上进一步优化核函数；模型4：ICS-MKELM模型，其主要是在MKELM模型基础上进一步优化连接权值。通过统计得到4类模型的平均相对误差变化，如图3所示。据图3，随趋势项预测模型的递进优化处理，对应模型的平均相对误差值呈减小趋势，验证各优化处理步骤的必要性和有效性。

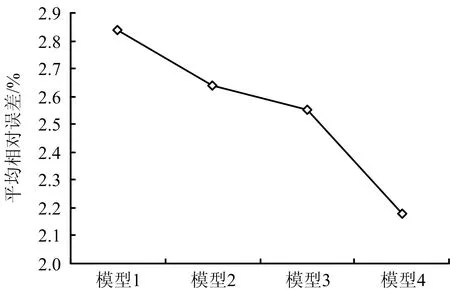
图3 趋势项递进优化处理的变化曲线Fig.3 Change curve of progressive optimization processing of trend term

综上，模型参数优化虽能不同程度的提高预测精度，但其平均相对误差为2.18%，预测效果一般，加之数据分解过程产生的误差项，使预测误差相对偏高，侧面验证误差修正预测的必要性。

③误差修正预测分析。利用Arima模型对误差序列进行修正预测，结果见表7。由表7可知，在TP01监测点的中期预测结果中，相对误差间于1.72%～2.03%，平均相对误差为1.89%；在TP12监测点的中期预测结果中，相对误差间于1.77%～2.03%，平均相对误差为1.91%；2者均优于趋势项的预测精度，验证Arima模型的误差修正能力，初步说明预测模型具有较优的预测效果。

表7 误差修正后的中期预测结果Table 7 Medium-term prediction results after error correction

2)后期预测结果分析

为进一步验证本文预测模型的有效性和滚动预测能力，实现滑坡位移的外推预测，对滑坡后期变形进行位移预测，结果见表8。

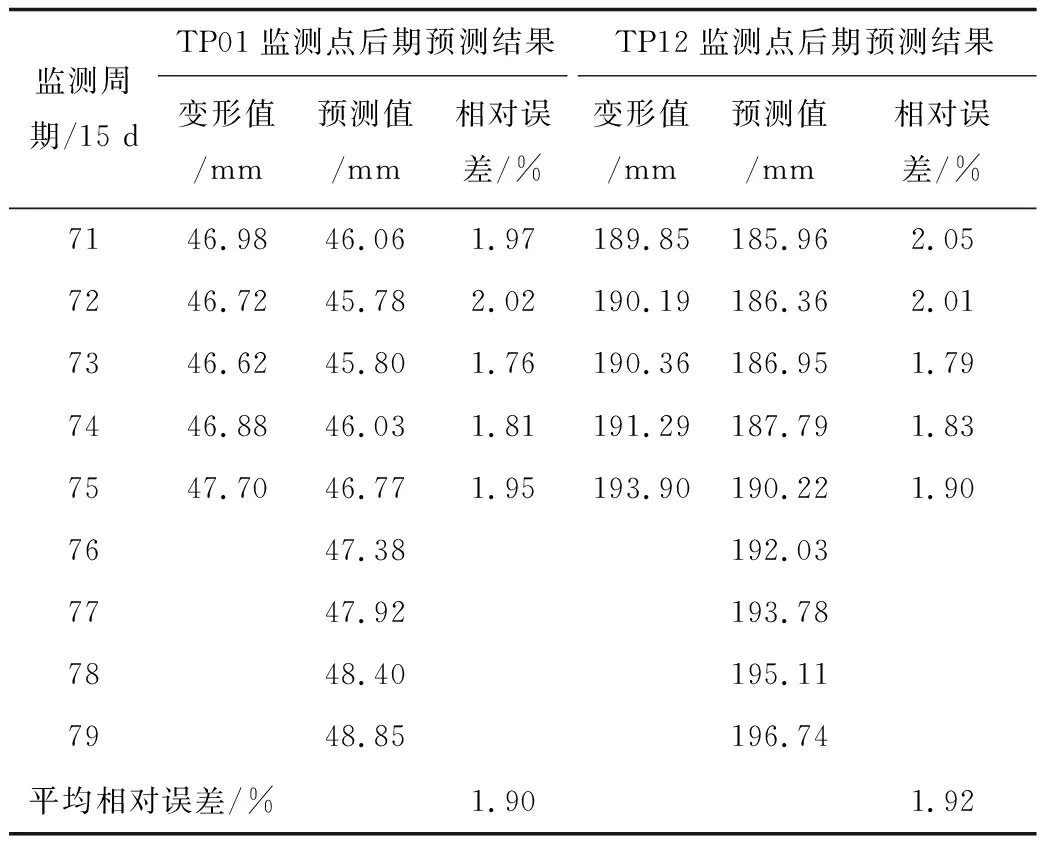
表8 滑坡后期预测结果Table 8 Prediction results of landslide in later stage

由表8可知，在TP01监测点的后期预测结果中，相对误差间于1.76%～2.02%，平均相对误差为1.90%；在TP12监测点的后期预测结果中，相对误差间于1.79%～2.05%，平均相对误差为1.92%；2者预测效果相当，与中期预测精度较为一致，预测精度均较高，充分验证本文预测模型适用性及滚动预测能力。同时，通过外推预测，得出2监测点的位移变形仍会进一步增加，应切实加强灾害防治，避免成灾损失。

通过前述分析，验证了组合预测思路在滑坡位移预测中的适用性，其不仅具有较高的预测精度，还具有较强的滚动预测能力，预测效果较好，可合理评价滑坡位移的发展趋势。

2.3 可靠性验证分析

考虑滑坡TP12监测点具有突变特征，以其第2次突变变形为例，进一步进行预测分析，以验证突变条件下的预测效果，验证样本是56～60周期；利用GM(1,1)模型和支持向量机模型进行类似预测，以进一步佐证预测思路的可靠性。

经计算统计得突变阶段的预测结果见表9。据表9，在突变阶段的预测结果中，相对误差间于2.03%～2.14%，平均相对误差为2.08%，略大于中、后期预测结果的平均相对误差值，但仍具较优的预测效果，说明滑坡突变变形会对预测效果具有一定影响，但影响有限。

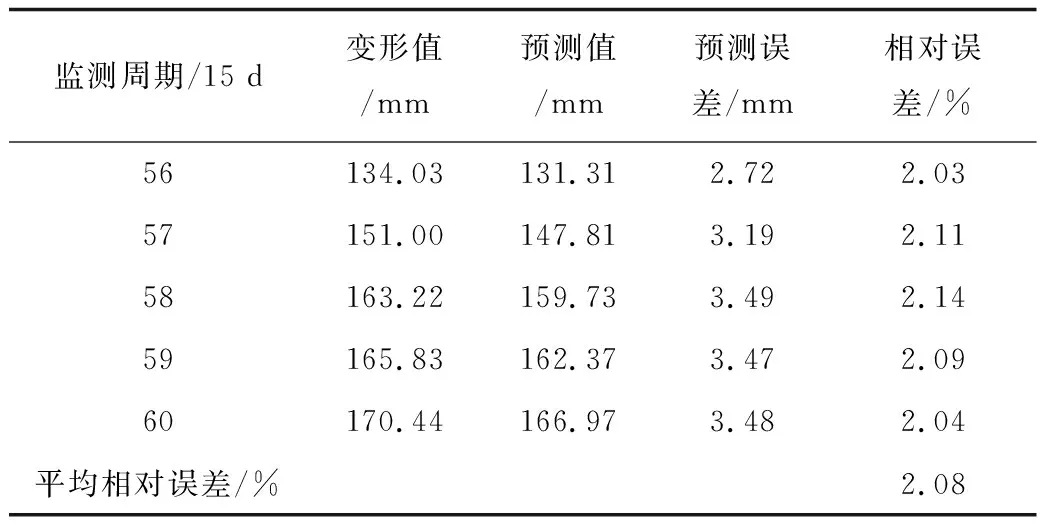
表9 突变阶段的预测结果统计Table 9 Prediction results statistics of mutation stage

统计本文预测模型和2类传统预测模型的预测结果，见表10。据表10，对比3类模型的预测效果，在预测精度方面，本文预测模型具有相对最小的平均相对误差值，说明其预测效果相对最优；GM(1,1)模型和支持向量机模型的预测效果相当，但明显不及本文预测模型的预测精度；在收敛速度方面，本文预测模型具有相对最短的训练时间，也明显短于GM(1,1)模型和支持向量机模型的训练时间，说明预测模型具有相对更快的训练速度。