基于一阶LADRC控制的直驱风机次同步振荡抑制策略

蔡维正，郭昆丽，刘璐雨，吴朝俊

(西安工程大学 电子信息学院，陕西 西安 710048)

0 引言

近年来国内外新能源并网诱发宽频带振荡事故频发，美国Texas双馈风电场、中国沽源双馈风电场，在线路串联补偿的情况下均出现次同步振荡 (subsynchronous oscillation , SSO)现象，主要原因是双馈风机换流器控制与线路补偿相互交互影响[1-2]。2015年7月1日，新疆哈密地区大规模直驱式风电场在电网没有串联补偿的情况下发生严重SSO事故，次同步频率扰动分量沿输电线路传播扩散到整个哈密电网，导致300 km外的3台大型火电机组切机[3]。

对于风电场与电网交互引发SSO这一现象，国内外学者做了广泛的研究。文献[4-7]研究表明直驱式永磁同步风电场并联弱交流电网诱发SSO，主要是由网侧逆变器与并联电网相互影响产生。文献[8-9]经过优化系统的控制参数来降低SSO风险，但是控制器的参数改变可能会对风机的运行状况产生影响。文献[10-12]提出在直驱式永磁同步风机网侧控制器附加控制策略抑制SSO。文献[13-15]提出在模块化多电平换流器(modular multilevel converter，MMC)、制氢系统、柔性装置等外部设备附加阻尼控制策略抑制SSO。文献[16-17]提出附加自抗扰控制 (active disturbance rejection control, ADRC)策略抑制 SSO，利用ADRC控制器替换传统附加控制策略的比例和移相环节，但是控制器参数整定过于复杂。附加控制策略针对单一次同步扰动分量进行抑制，难以适应风电场多变化的运行工况。文献[18-20]提出ADRC控制器代替传统的电流内环PI控制器，可以有效抑制SSO，具有强鲁棒性，但其控制器参数多难以整定。

本文提出基于一阶线性自抗扰控制(linear active disturbance rejection control，LADRC)电流内环控制器抑制SSO的策略，通过建立网侧逆变器的数学模型，分析次同步频率扰动分量的传输机理，对一阶LADRC电流内环控制器参数进行优化设计及整定。通过PSCAD/EMTDC仿真结果验证本文方法抑制SSO的可行性和有效性。

1 数学建模及SSO机理分析

1.1 直驱式永磁同步风电机组数学模型

直驱式风电机组主要由风轮机、永磁同步发电机、机侧变换器、网侧变换器及其控制系统构成。由于次同步振荡主要是由网侧变换器及其控制系统与并网系统动态交互引起，因此将风轮机、永磁同步机、机侧变换器及其控制系统简化等效为受控电流源[4,6-8,13]。图1为简化后的直驱式风电机组网侧逆变器及其控制结构。图1中：、、分别为abc坐标系下并网点电流、电压和网侧逆变器输出电压；、、、分别为dq坐标系下并网点电流和电压；、、分别为控制器电流和直流侧电压参考值；、分别为控制器输出dq坐标系下参考电压；为直流侧电压；为等效直流受控电流源；为直流侧输出电流；、分别为滤波和线路电感；C为直流侧电容；为电网同步角速度；为锁相环输出相角。

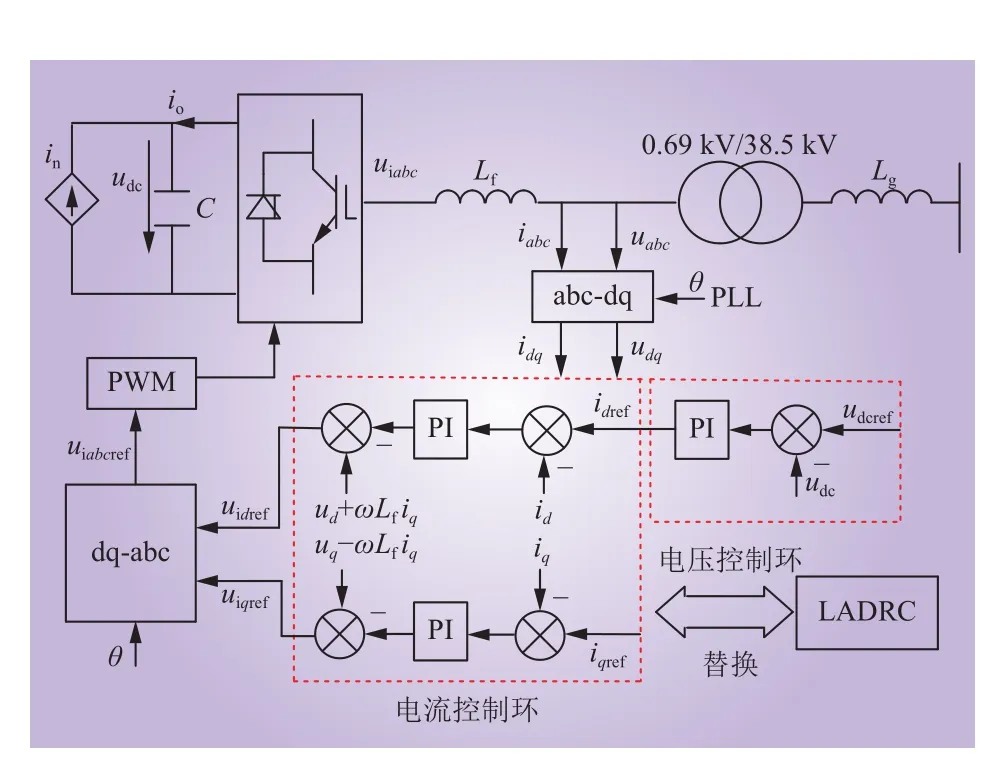
图1 网侧逆变器及其控制结构Fig. 1 Grid-side inverter and its control structure

规定流入网侧逆变器为正方向，其模型为

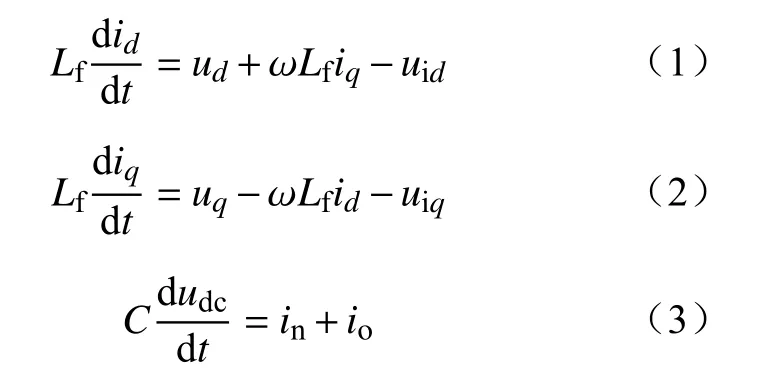
由式(1)(2)可知，dq轴电流存在耦合关系，须对PI控制器进行解耦控制。在图1中，锁相环PLL跟踪并网点电压的相位角，用于对电压电流进行坐标变换；控制系统分为电压外环和电流内环控制，电压外环控制可维持直流母线电压稳定，电流内环采用有功无功解耦控制，可实现有功和无功的单独调节，控制器输出dq轴的参考电压值、，经过反派克变换形成三相交流电压的参考值、、，经过PWM调制环节产生触发脉冲，控制逆变器桥臂的开通与关断，最终在逆变器的输出口形成电压。

1.2 SSO机理分析

大规模直驱风机接入弱交流电网诱发次同步振荡现象，主要是由风电机组网侧逆变器及控制系统与并联交流电网之间相互作用所产生[4-5]。直驱风电场接入弱电网受扰动后，在并网点产生频率为的次同步频率电压和电流扰动分量，扰动分量馈入网侧逆变器控制系统，分别与锁相环、电流环等环节耦合出频率为的扰动量，最终在网侧逆变器并网点产生频率为的扰动分量、，在一定条件下，新的次同步分量叠加在原有的次同步分量上产生更大的扰动，以此形成正反馈机制，使系统振荡发散失稳[6-7]。其反馈路径如图2所示。

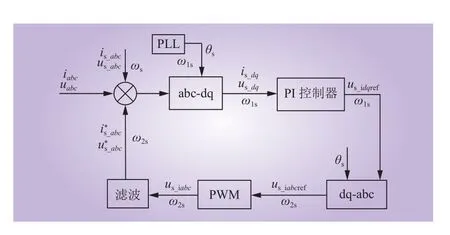
图2 扰动量反馈路径Fig. 2 Disturbance propagation path

综上，次同步频率扰动分量馈入电流内环PI控制系统产生新的次同步频率分量，导致系统失稳。传统的PI控制器的抗扰能力和鲁棒性差，难以适应弱交流环境[18-20]。本文采用一阶LADRC来代替电流内环的PI控制器，其控制器经过线性扩张状态观测器实时跟踪输出电流和补偿扰动，从而阻断次同步分量的传播来抑制SSO。

2 LADRC控制策略

文献[21]提出ADRC控制技术，根据被控对象输入输出信息对扰动进行估计，并采用非线性状态误差反馈对系统的扰动给予补偿。在此基础上，文献[22]提出将非线性ADRC简化为LADRC，大大减少控制器参数。本文采用LADRC将控制器参数减少为3个，易于设计及整定。LADRC控制器由3部分组成：线性微分跟踪器(linear tracking differentiator, LTD)、线性扩张状态观测器 (linear extended state observer, LESO)和线性状态 误 差 反 馈 控 制 律 (linear state error feedback,LSEF)。由于LTD影响内环响应速度，本文忽略该环节，只进行LESO及LSEF的设计。

2.1 电流内环LADRC控制器

根据1.2节SSO产生机理分析可知，PI控制器对次同步扰动量抑制能力差，导致次同步扰动量扩散使系统失稳。根据SSO的产生机理设计LADRC控制器，由于dq轴具有结构对称性，故以d轴为例进行说明。将式(1)写成包含次同步扰动分量的形式，即

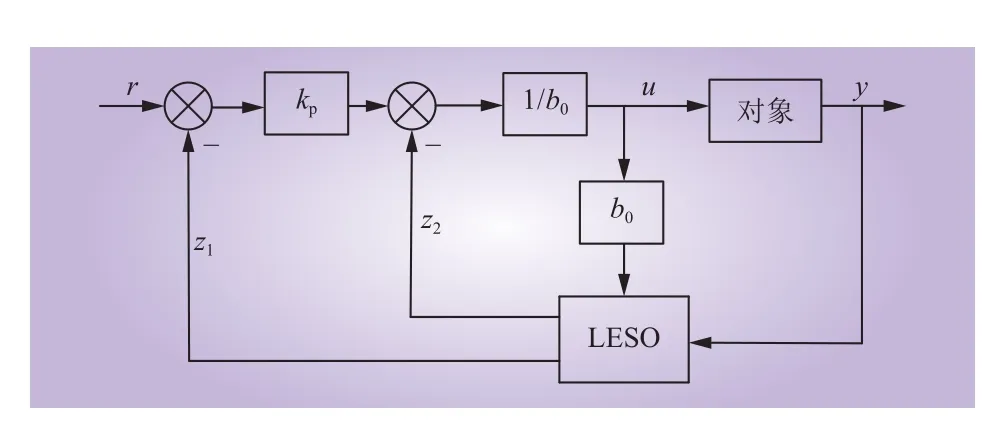
图3 基于LADRC的电流内环控制器Fig. 3 Inner-loop current controller based on LADRC

2.2 LESO分析及参数整定

LESO估计的准确性和快速性将直接影响LADRC的控制性能。下面分析对LESO的性能影响。对(13)式进行拉普拉斯变换并代入增益矩阵L，计算出为

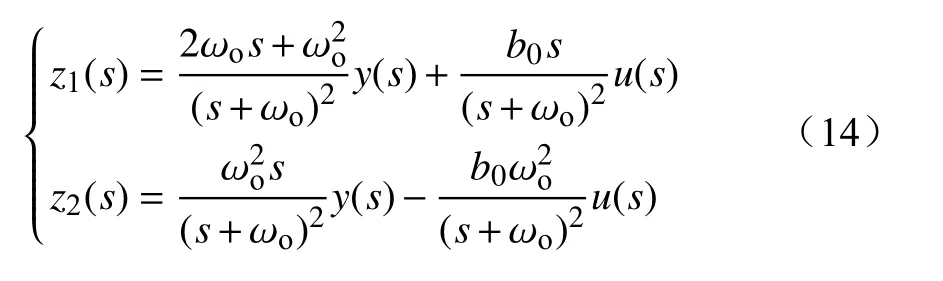
一方面，网侧逆变器输出电压电流存在开关频率附近的高频谐波，测量信号中的高频谐波分量对LESO有较大的影响。另一方面，直驱式风电场接入弱交流电网产生次同步分量，振荡频率为10～50 Hz。在传统的控制系统中，次同步频率扰动量通过PI控制系统产生含有次同步频率扰动的参考信号，导致系统失稳，称其扰动信号为输入扰动。下面分析对测量噪声和输入扰动的影响，、至的传递函数为

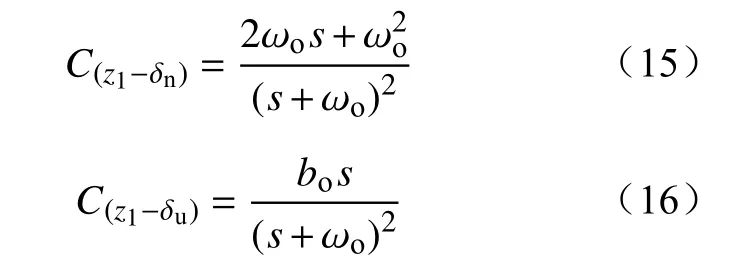
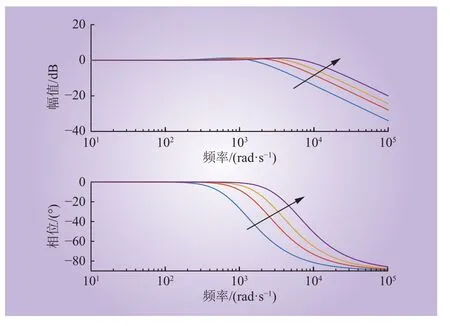
图4 bode图Fig. 4 Bode diagram of transfer function

图5 bode图Fig. 5 Bode diagram of transfer function

LESO对扰动的快速准确估计将直接影响LADRC补偿扰动的有效性。下面分析LESO对扰动的跟踪性能，根据式(9)(10)求得LESO的观测误差为

对(17)进行拉式变换得出误差传递函数为

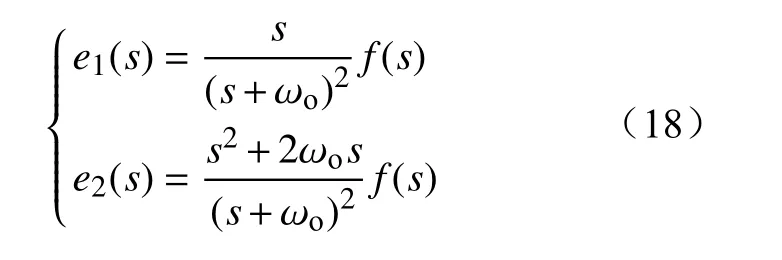
则总扰动至观测误差的传递函数为

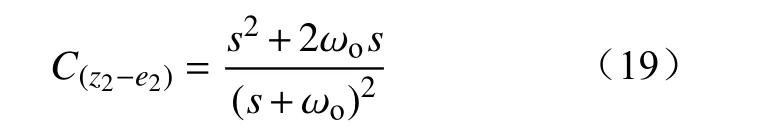
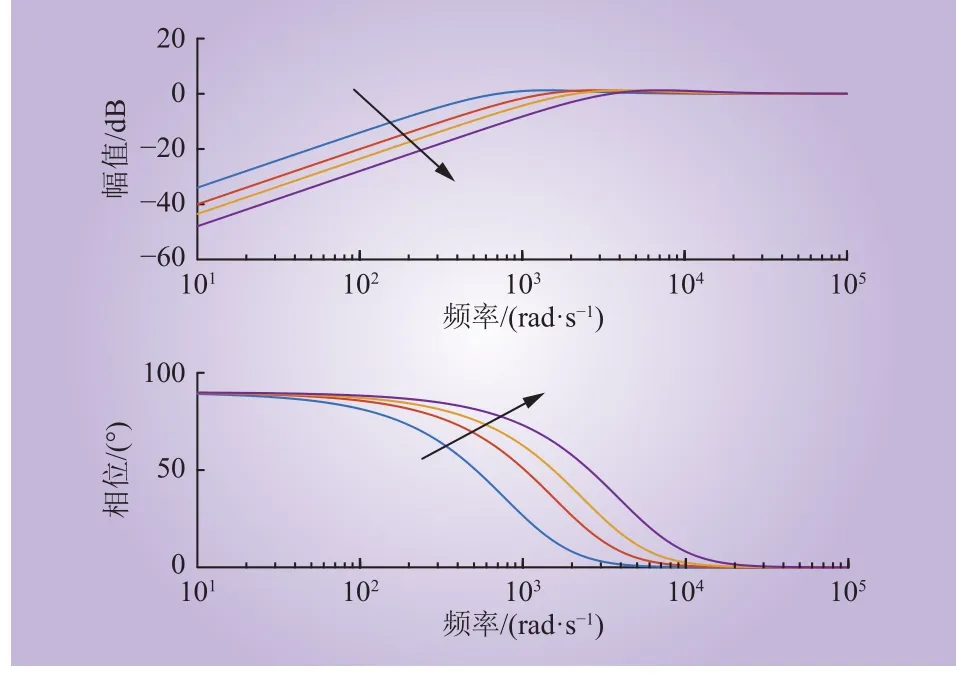
图6 bode图Fig. 6 Bode diagram of transfer function

2.3 LSEF参数整定

对式(20)进行拉式变换得到y与r之间的传递函数为

图7 bode图Fig. 7 Bode diagram of transfer function

2.4 稳定性分析

下面采用内模控制器[24-25]等效的方法对LADRC的电流控制器进行鲁棒性分析，研究逆变器内环系统的稳定性。将状态空间表达式(13)进行拉式变换，得到

根据式(23)，网侧变换器的LADRC闭环电流控制结构如图8所示。

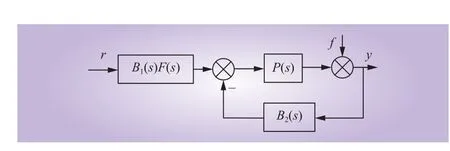
图8 LADRC闭环结构Fig. 8 LADRC closed-loop structure

为分析LADRC闭环控制的鲁棒性，将基于LADRC的电流内环控制系统结构变换为TDFIMC反馈控制结构，如图9所示。图中：P(s)为网侧变换器实际模型；P0(s)为被控对象名义模型；Q1(s)为IMC定点跟踪控制器；Q2(s)为IMC扰动抑制控制器。

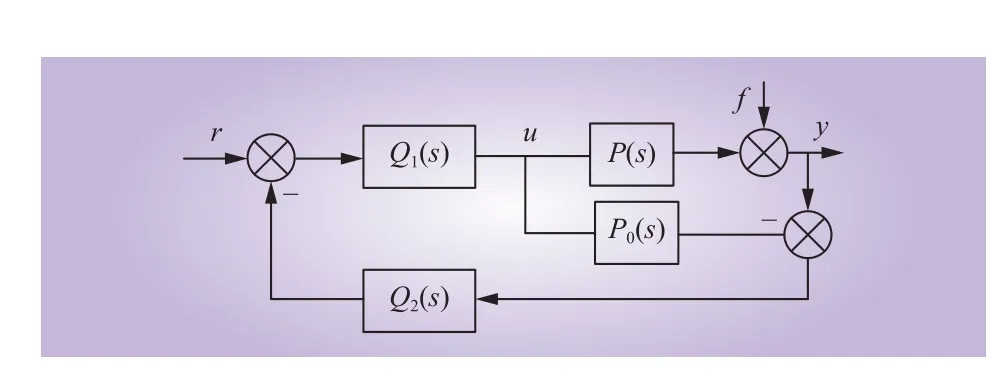
图9 TDF-IMC等效框架Fig. 9 TDF-IMC equivalent framework

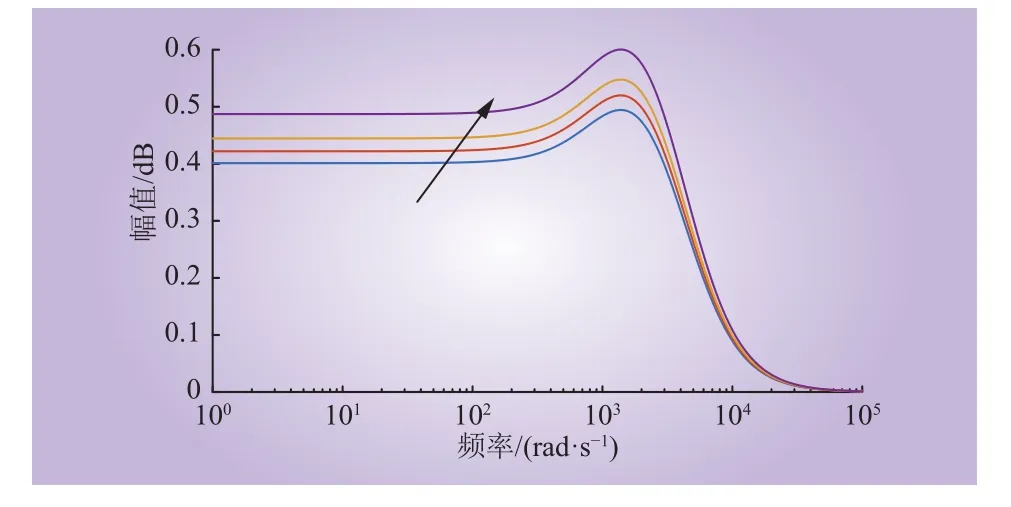
图10 Q 1(jω)[P(jω)− P0(jω)]Q2(jω)bode图Fig. 10 Bode diagram ofQ1(jω)[P(jω)− P0(jω)]Q2(jω)

3 仿真验证

3.1 参数设置

为验证本文所提策略抑制SSO的有效性，在PSCAD/EMTDC仿真软件中建立如图1所示等值模型。采用一台网侧逆变器模型并联受控电流源等效200台直驱式风机，进行传统PI控制和本文控制策略仿真实验分析。系统参数如表1所示。

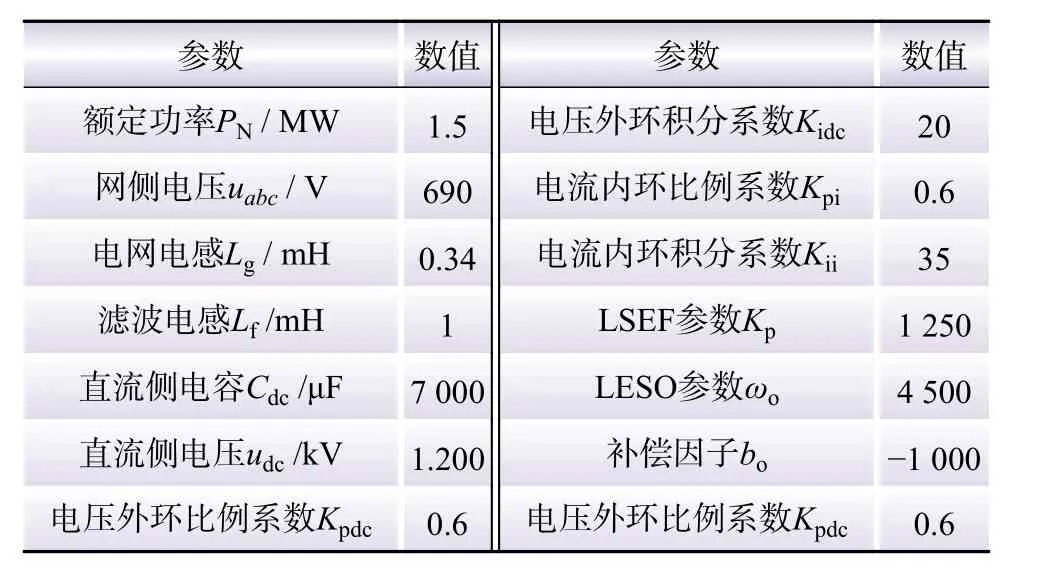
表1 单台网侧逆变器参数Table 1 Parameters of a grid-side inverter

3.2 不同电网强度下控制策略对比分析

设置风速为7.5 m/s，风电场出力稳定后，在2 s通过投入线路电感Lg，模拟弱交流电网触发SSO，对比分析PI控制与LADRC控制策略运行情况。根据IEEE标准1204—1997 的定义，交流电网短路比 (short circuit ratio，SCR)小于 3 的电网即为弱电网，小于2的电网为极弱电网。通过投入2组电感来研究不同弱电网强度下LADRC的抑制情况。仿真结果如图11所示，图11 a)为投入电感Lg=0.006 7 H，经过计算，短路比为2.4，图11 b)为投入电感 Lg=0.007 3 H，经过计算，短路比为2.2。采用PI控制时，网侧变换器输出功率、直流侧电压、A相电压电流迅速振荡发散，导致整个系统失稳。采用本文控制策略时变换器输出功率和直流侧电压、A相电压电流只出现短暂的瞬态过程就进入稳定运行状态。另外，随着等效线路电感值增加，短路比SCR由2.4降低至2.2，PI控制策略下并网系统的次同步分量发散速度加快，振荡幅值增大，导致系统迅速失稳，而在LADRC控制策略下仍保持稳定运行。

图11 不同电网强度下PI和LADRC控制策略对比Fig. 11 Comparison of PI and LADRC under different power strength

在SCR=2.2的弱电网情况下，对A相电流进行频谱分析，如图12所示，图12 a)为PI控制时的频谱，A相电流含有2组大幅值的次/超同步频率分量[7]，分别为 41.4 Hz 和 58.6 Hz、33 Hz 和67 Hz；图 12 b)为 LADRC 控制策略的频谱图，A相电流频谱只包含50 Hz的工频量，并未出现其他次/超同步分量。这表明LADRC内环控制器能够阻断次同步分量的传播，有效抑制SSO。

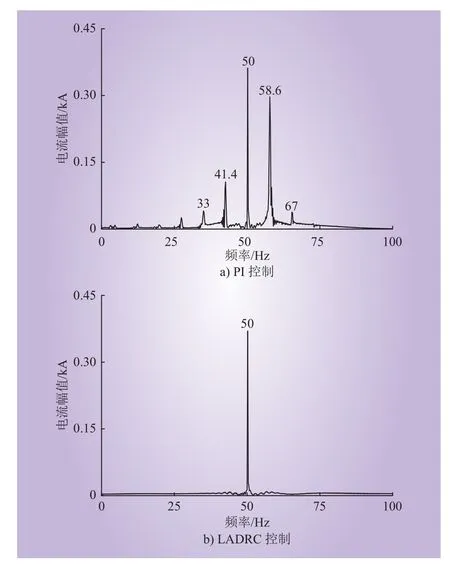
图12 PI和LADRC控制FFTFig. 12 FFT controlled by PI and LADRC

3.3 策略适应性分析

为验证本文所提策略抑制直驱式风机诱发SSO的适应性，对风电场风速阶跃工况、短路工况和极弱电网这3种运行工况进行时域仿真分析。

工况1：风机以风速为7.5 m/s运行至稳定。在 2 s时投入线路电感 Lg=0.007 3 H，在 2.5 s设置风速阶跃至9.5 m/s，运行至3.5 s时风速阶跃至5.5 m/s。结果如图13所示，采用PI控制策略风电场的有功输出和A相电压电流迅速出现SSO，采用LADRC控制仍然能够稳定运行。

图13 风速阶跃工况Fig. 13 Operating conditions of wind speed steps

工况2：在变压器高压侧设置单相接地故障，在2s时投入线路电感Lg=0.007 3 H，稳定运行后，在2.5 s时在38.5 kV母线侧设置A相短路故障，持续100 ms。结果如图14所示，采用LADRC控制策略的风机输出功率和 A相电压电流出现了约0.3 s的瞬态过程，没有出现SSO。

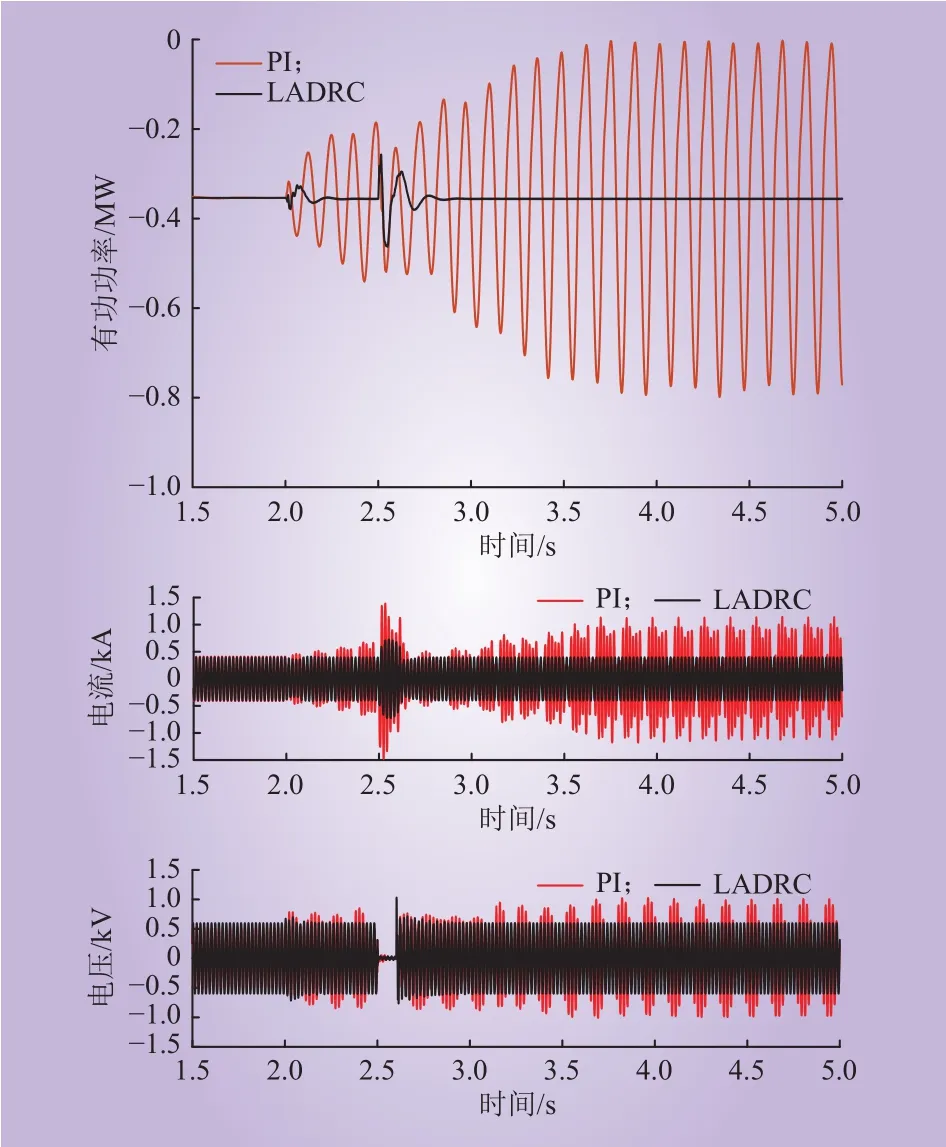
图14 单相短路工况Fig. 14 Single-phase short-circuit conditions

工况3：设置SCR=1.9的极弱电网运行工况，在 2 s时投入等效电感 Lg=0. 008 5 H，并联电网系统为极弱电网，结果如图15所示，在 PI控制策略下风电场有功、A相电压电流迅速出现SSO，在本文LADRC控制方式下风电场仍稳定运行。

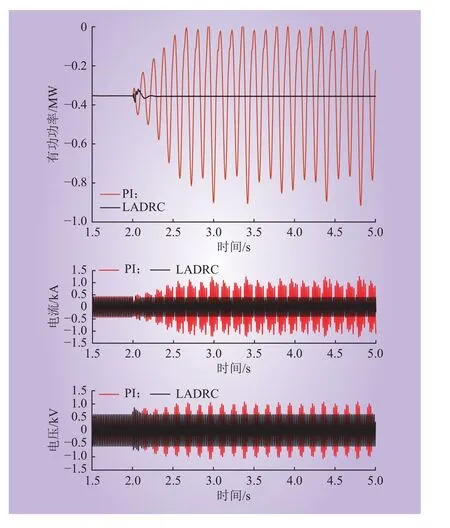
图15 极弱电网工况Fig. 15 Operating conditions of very weak grids

通过对上述3种工况进行仿真分析，结果表明在多变的环境下LADRC内环控制器仍能够阻断次同步分量的传播，有效抑制SSO。

4 结论

针对直驱式风机并联弱交流电网诱发SSO问题，本文提出了一种具有鲁棒性强的LADRC电流内环控制器抑制策略。根据网侧逆变器的数学模型和SSO扰动机理设计一阶LADRC控制器，优化整定内环控制器参数、。分析表明带宽增加能够提高LESO对次同步扰动分量估计的准确性和快速性，使得LSEF环节能够准确地补偿次同步扰动分量。仿真结果表明本文所提出的控制策略能够阻断次同步分量的传播从而抑制SSO，并且能适应多工况运行。