基于加权马氏距离型TOPSIS算法的10 kV配电网雷害风险评估

杜岩，谢从珍，李彦丞，谢心昊，栾乐，罗思敏

(1. 华南理工大学 电力学院，广东 广州 510641；2. 广东电网有限责任公司广州供电局 ，广东 广州 510013)

0 引言

雷击是威胁电力系统稳定性的重要因素。相对于主网较为完善的避雷措施，10 kV配电网架空线路基本无避雷线架设，且接地方式通常为混凝土杆自然接地，绝缘水平相对较低[1-2]。而配电网作为与用电设备直接相关的电力输送通道，其供电可靠性和安全性需求日益提高。近年来，以监督学习为代表的机器学习算法在电力领域常用于负荷预测、线损预测[3]，以及变压器状态预测[4]。对于数据质量较低的10 kV配电网线路，机器学习等算法难以实现令人满意的雷害评估结果。综上，亟须建立有针对性的10 kV配电网雷害风险评估体系。

传统的雷击跳闸评估方法主要基于雷击跳闸机理，由于计算量过大、模型构建过于复杂等问题，在电网评估层面可实现性较差。文献[5-6]对10 kV架空线路雷击跳闸率计算模型进行改进，并展开差异性防雷工作。层次分析法[7]常被用于主配电网的雷击跳闸风险评估；文献[8]构建了多层级雷害评估体系，然而此方法评估主观性较强；文献[9]基于多维数据融合对主网雷害风险进行评估，但在指标构建方面置信度较低，且权重仅考虑数据熵值，存在与客观事实相悖的风险。

TOPSIS算法是一种逼近理想解的排序方法[10]，首先基于评估样本构造最佳与最劣对比序列，计算各样本与对比序列之间的距离，最终根据各样本与对比序列的相对贴合度完成评估[11]。TOPSIS算法对数据质量要求低于机器学习，且数学意义明确。在电力领域，文献[12]采用灰色关联算法与TOPSIS算法结合对主网的网架结构进行评价，但该方法缩小了样本间的差异性，降低了评估灵敏度。为消除指标间相关性的影响，文献[13]采用广义加权马氏距离代替传统TOPSIS算法中的欧氏距离对防洪调度决策进行评估，取得了较为贴合实际的评估结果。因此，可考虑将加权马氏距离型TOPSIS算法应用于10 kV配电网雷击跳闸风险评估。

本文按照评估单元构建、指标选取与量化计算、指标组合赋权、TOPSIS算法计算和风险分级的顺序完成10 kV配电网雷害风险评估。并以广州市历史跳闸统计数据对评估结果进行有效性验证。

1 基于 10 kV 配电网线路特征的评估单元

主网线路常以杆塔为单元进行雷击跳闸风险评估。相较于主网，10 kV配电网线路存在以下特点：杆塔数量众多、线路分布错综复杂、绝缘配置较为简单、杆塔以钢筋混凝土杆为主，以及单条馈线由多条支线与干线交织形成等。若参考主网以杆塔为单元进行配电网线路雷击跳闸评估，则存在评估单元间差异性较小、计算难度较大等问题。

因此，本文采用网格法对线路进行划分。参考主网线路雷电参数统计网格划分标准，选择0.01°×0.01°(约 1 km×1 km)大小的经纬度单元网格对评估区域进行划分。本文后续指标计算与风险评估均以此网格为单元。

2 10 kV 配电网线路雷击跳闸评估指标构建

雷击跳闸风险与地区落雷活动、线路绝缘水平及走廊建筑物等要素密切相关[14]。对避雷器、杆塔、绝缘子、导线及接地电阻进行指标量化计算以反映线路绝缘水平。线路走廊综合考虑走廊屏蔽物对直击雷的影响及土壤电阻率对感应雷的影响进行指标构建。综上，本文选取10项雷害风险评估指标，如图1所示。

图 1 雷害风险评估指标Fig. 1 Lightning tripping risk assessment index

2.1 线路走廊落雷活动强度系数

作为最直接的气象影响因素，线路走廊落雷活动的强弱直接影响线路的雷击跳闸率。中国10 kV配电网线路耐雷水平较低，通常不架设避雷线，且避雷器无法实现全线保护。因此，落雷活动越强烈的地区线路雷击跳闸风险越高。基于线路走廊雷电监测系统数据，计算每个网格内落雷密度值作为其落雷活动强度系数，第i个网格的落雷活动强度系数为

式中：n为统计年数；S为单元网格面积；N(i)为n年第i个网格内落雷次数总和。

2.2 线路走廊环境指标

2.2.1 线路走廊落雷易击性系数 γ2

10 kV配电网线路常分布于城区，线路走廊分布大量建筑物与林地。由于杆塔高度较低，线路走廊中的树木和建筑物对直击雷起到一定屏蔽作用。常被用于表征树木和建筑物对直击雷屏蔽效果的屏蔽系数[15]对于实际运行环境复杂的线路而言可实现性较差。因此，量化走廊环境中屏蔽物与线路雷击跳闸的关系可以更准确地反映雷电屏蔽效果。

式中：t(i)为第i个网格n年内雷击跳闸次数。

上式为统计数据所得落雷易击性系数，因此需量化线路走廊屏蔽物与落雷易击性系数关系。根据线路走廊土地利用情况，提取分析每个网格内建筑物以及林地信息。以网格内建筑物占地比例与林地分布情况将网格划分为建筑物类型网格、林地类型网格以及农田类型(对线路无屏蔽保护作用)网格。

对于建筑物类型网格，落雷易击性系数与网格内建筑物占地比例、最高建筑物高度以及平均建筑高度具有较强关联性。以广州市为例，计算得出建筑物类型网格落雷易击性系数相关性系数表如表1所示。

表1 建筑物类型网格落雷易击性系数相关性分析Table 1 Correlation analysis of lightning vulnerability coefficient of building type mesh

选取网格内上述3项建筑物指标与落雷易击性系数作线性回归，得出建筑物类型网格落雷易击性系数公式为

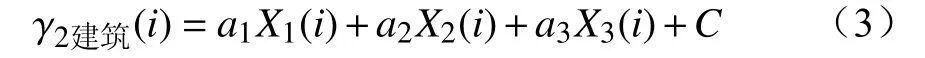
对于林地类型网格以及农田类型网格，以统计数据所得落雷易击性系数的平均值作为对应类型网格的落雷易击性系数。

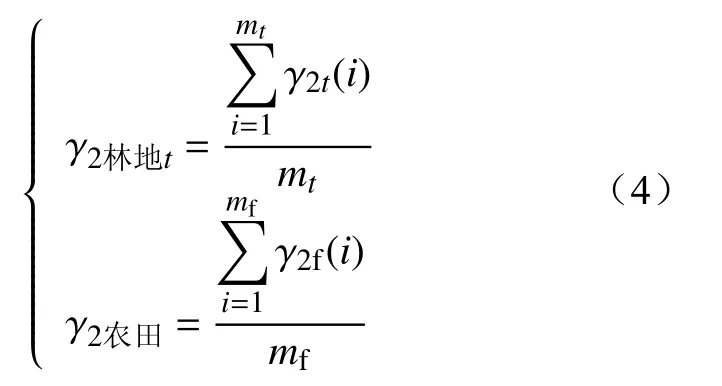
2.2.2 线路走廊土壤电阻率系数 γ3

大地土壤电阻率影响雷电感应过电压波形的畸变与峰值的高低。研究表明，10 kV线路感应过电压幅值随着土壤电阻率的增大而提高[16]。因此，本文选取线路走廊土壤电阻率作为一项雷击跳闸风险评估指标。提取网格内土壤信息，采用估算模型计算网格的土壤电阻率[17]，即

式中：S(i)为第i个网格的含盐量；ω为含水率（＞5%）。

2.3 线路本体参数指标

2.3.1 线路避雷器密度系数 γ4

10 kV配电网线路加装避雷器可有效提升线路耐雷水平。线路雷击跳闸概率随线路避雷器密度的增大而降低。以单位网格内避雷器安装数量与杆塔数量之比计算避雷器密度，并对密度值进行正向化处理完成避雷器密度系数构造。即避雷器密度系数越大，雷击跳闸风险越高。

2.3.2 线路避雷器年限系数 γ5

避雷器性能随投运年限的延长而下降。本文以实际运行避雷器数据构建投运年限与故障率映射关系。基于网格内所有避雷器的投运年限，选取映射故障率最大值为网格的避雷器年限系数，即

雷电流冲击残压作为避雷器的重要性能参数，可反映对线路的保护水平。避雷器残压高，表明雷电流作用下被保护设备承受最高电压较高，则设备损坏风险较大。选取网格内所有避雷器雷电冲击电流残压最大值作为网格的避雷器型号系数，即

式中：Up(i)max为网格i内避雷器雷电冲击电流残压最大值。

2.3.4 线路塔型系数 γ7

基于线路耐雷水平综合等值法模型可知，在雷电直击线路时，线路耐雷水平随线路杆塔电感与高度的增大而降低。在感应雷电过电压的作用下，线路过电压峰值与杆塔高度近似呈正比关系。因此，杆塔电感值与杆塔高度直接影响线路雷击跳闸风险。为简化计算，考虑到杆塔电感值与杆塔高度成正比关系，可在网格内杆塔电感值对塔型系数进行构造以简化计算。10 kV配电网线路以混凝土塔及铁塔为主，选取2种杆塔的等值电感计算网格内所有杆塔电感值之和，得到线路网格的塔型系数，即

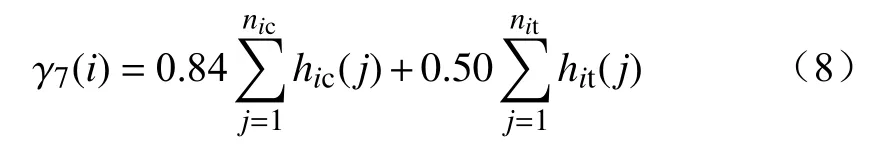
式中：0.84与0.50分别为混凝土杆塔和铁塔的参考等效电感值[18]；nic、nit分别为网格i内混凝土塔数量和铁塔数量； hic(j)、hit(j)分别为网格i内第j个混凝土塔高度和网格i内第j个铁塔高度。

2.3.5 线路绝缘子系数 γ8

10 kV配电网线路绝缘子以瓷式绝缘子为主，属于不易损设备。然而绝缘子的机械强度随着投运年限的延长逐渐降低，在线路遭受雷击时绝缘子发生损坏的风险显著提高。基于统计数据进行关联计算，可得出绝缘子雷击故障率与投运年限的关联关系，然而该方法需要大量样本数据，且关联结果可靠性较低。Weibull模型常被用作电力设备的寿命预测，而对于不易损坏的绝缘子，本文结合绝缘子台账数据与雷击跳闸绝缘子损坏数据筛选出无失效绝缘子样本，采用二参数无失效数据Weibull模型对线路绝缘子雷击损坏失效风险进行描述。线路绝缘子在雷击时损坏的概率密度函数与分布函数如式（9）和式（10）所示。

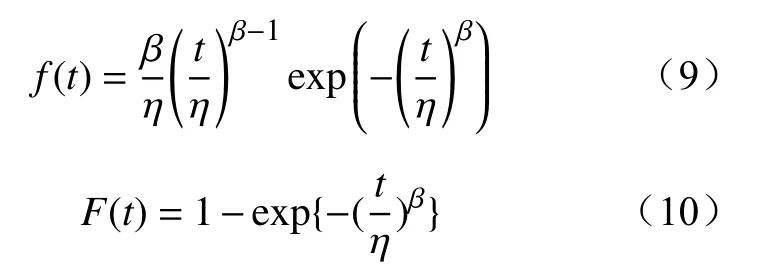
式中：t为运行时间；β为形状参数；η为尺度参数，本文拟合计算得到 η=4 816.183 2，β=3.767。

线路绝缘子随投运年限变化在雷击时损坏失效的概率[18]为

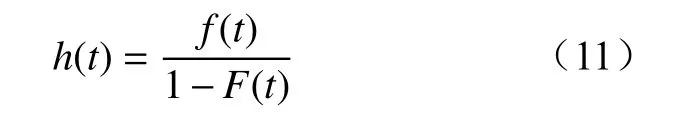
计算网格中所有绝缘子在雷击时损坏失效的概率，选取每个网格中失效概率最大值作为此网格线路绝缘子系数，即

式中：himax为网格i中所有绝缘子在雷击时失效概率的最大值。

2.3.6 线路线型系数 γ9

10 kV配电网线路导线分为裸导线与绝缘导线2种。绝缘导线的使用可以显著提高线路耐雷水平，因此绝缘导线在遭受雷击时发生跳闸的概率远低于裸导线。本文根据2类线型在雷击跳闸时的实际故障率设定网格内线型系数为

式中：Rlb、Rli分别为裸导线和绝缘导线故障率；nlb(i)、nli(i)分别为网格i中裸导线与绝缘导线数量。

2.3.7 接地电阻系数 γ10

接地电阻直接影响线路耐雷水平。杆塔遭受直击雷时，较高的接地电阻将显著提升横担对地电位，设备绝缘击穿风险随之增大。本文以网格内杆塔接地电阻值之和构造接地电阻系数。

10 kV架空线路以混凝土塔及铁塔为主，其中混凝土塔常采用直接接地方式。由于杆塔数量众多，对于铁塔可采用设计值进行计算；对于混凝土塔，电杆横担抱箍与杆塔内钢筋有效连接时可取 50 Ω 进行计算[19]。

3 10 kV 线路雷击跳闸评估模型

本文雷击跳闸风险评估流程如图2所示。首先基于上文构造的10项系数雷击跳闸风险评估样本提取最佳与最劣对比序列，并且采用AHP与熵权法对十项系数进行组合赋权。以加权马氏距离型的TOPSIS算法对样本进行雷击跳闸风险评估，得出地理网格与馈线2个层面的风险值。最终根据数据特点进行风险分级，并以历史数据进行结果验证。

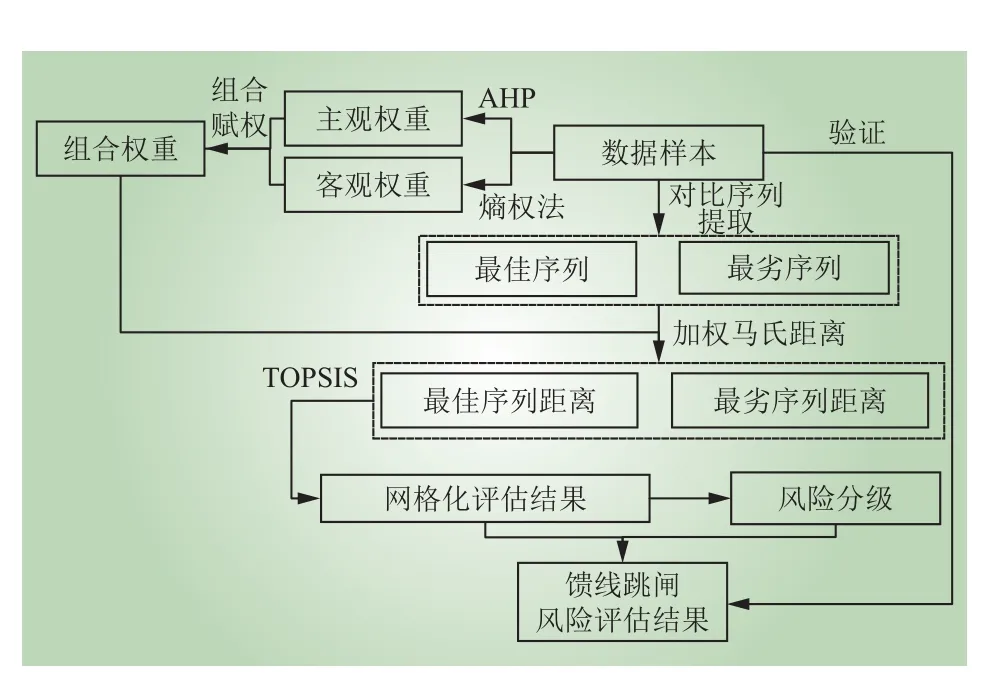
图 2 雷击跳闸风险评估算法流程Fig. 2 Lightning tripping risk assessment algorithm flow

3.1 组合赋权算法

对评估指标进行合理赋权可提高评估结果的准确性，现有的赋权方式分为以熵权法为代表的客观赋权和以AHP为代表的主观赋权两大类[20]，仅考虑AHP赋权时具有较强主观性且可解释性较差，而仅考虑熵权法则存在所得权重与实际经验相悖的风险。因此，本文结合AHP算法与熵权法进行互补，以获得更为合理的指标权重。

层次分析法AHP是一种解决多目标复杂问题的定性与定量相结合的决策分析方法[21]。由于AHP算法方案层的方案数目不能大于9，因此上文与避雷器相关的3项系数可统一归为避雷器指标系数进行权重计算，后续可进一步拆分计算3项系数的权重。以上文提出的评估指标作为方案层，以评估准确性、评估复杂性以及原始数据质量作为准则层对方案层进行评估，以雷击跳闸风险作为目标层，最终完成AHP算法赋权，得到权重

本文选取熵权法作为客观权重的计算方法。在信息论中，熵是对不确定性的一种度量。熵与样本的不确定性及所包含信息量的大小呈正相关关系[22]。设第i个网格(即第i个样本)第j项指标为xij，形成风险指标矩阵X={xij}m×10，m为样本数量。首先对指标进行无量纲化处理，则第 i个样本第j个指标值的比重pij为

得到客观熵权 λ2={λ2(1), λ2(2),···, λ2(10)}。

为获得更加合理权重值，本文采用组合赋权计算组合权重[23]，即

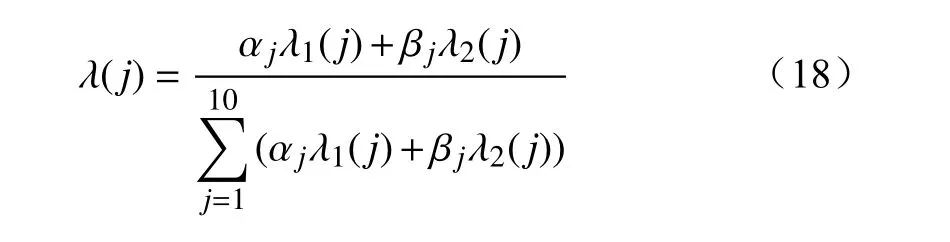
最终得到10项指标系数的组合权重λ={λ(1),λ(2),···, λ(10)}。

3.2 基于加权马氏距离的 TOPSIS 算法

TOPSIS即“逼近于理想值的排序方法”，是一种针多指标样本的评估方法。以各项指标在所有样本中的最优值和最劣值为对比序列，求出各样本与对比序列的接近程度，以获取评估结果排序。TOPSIS算法数学意义明确，能够较好地刻画多指标的综合影响力度，对于数据分布及样本量、指标多少无严格限制，既适于小样本资料，也适于多样本、多指标的大系统，较为灵活、方便，且具有数据敏感性低的特点。因此本文以TOPSIS算法为基准进行评估[24]。

传统的TOPSIS算法中使用欧氏距离计算样本与对比序列的距离，但考虑到各项指标取值范围差异较大，且指标间可能存在相关关系，使用欧氏距离难以对多项复杂指标对象进行合理评估。而独立于测量尺度的马氏距离不受坐标之间的量纲影响，且可以排除变量之间相关性的干扰。因此本文采用加权马氏距离代替欧氏距离进行计算。

首先以风险指标样本X={xij}m×10构造对比序列。选取样本中每项指标最小值构造最佳对比序列 C+={min xij| j∈[1,10]}，此序列代表理想雷击跳闸风险最小的样本；取样本中每项指标最大值构造最劣对比序列 C–={max xij| j∈[1,10]}，此序列代表理想雷击跳闸风险最大的样本。

计算每个样本与最佳、最劣序列的加权马氏距离，即

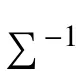
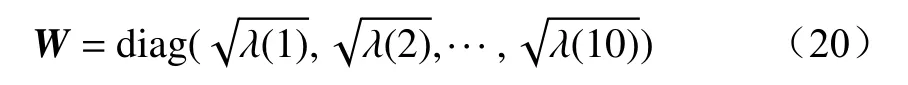
求出各样本与对比序列的加权马氏距离后，计算各样本与对比序列的相对贴近度，即

式中：si为第i个网格的雷击跳闸风险值。由上式可得，相对贴近度越大，表示样本与最佳对比序列相对距离越大，即表明样本雷击跳闸风险越高。由10 kV馈线所占网格的情况可得到以馈线为单元的雷击跳闸风险评估结果，即

式中：Yr为第r条馈线的雷击跳闸风险值；t为第r条馈线所占的网格数；为第r条馈线中第i个网格的相对贴近度。

3.3 雷击跳闸风险分级

得出馈线雷击跳闸风险值后，对r条评估馈线按照风险值降序排列，如图3所示。将馈线风险分为4级，选取所有馈线风险值之和的1/4值Tr作为等级划分阈值。若前k条馈线风险值之和大于等于Tr，则将前k条馈线设为一级风险馈线；若第k+1条馈线到第k+b条馈线风险值之和大于等于Tr，则设此b条馈线为二级风险馈线。以此类推，得到4种风险等级馈线。

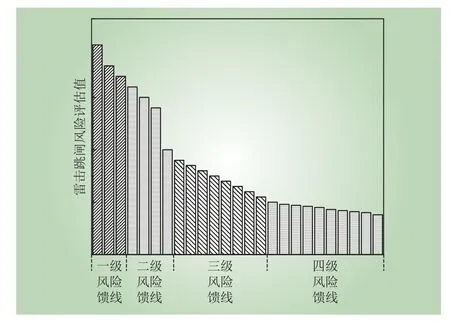
图 3 馈线雷击跳闸风险分级示意Fig. 3 Diagram of lightning trip risk classification

4 算例分析

本文数据来源如表2所示。

表2 数据来源Table 2 Data sources

基于上述评估方法对广州市3212条10 kV架空线路进行雷击跳闸风险评估。在权重计算方面，仅用熵权法计算得出绝缘子系数、避雷器年限系数及线型系数权重较高，而落雷活动系数权重较低，不符合客观事实。在综合权重方法下落雷活动系数、线性系数及避雷器年限系数权重较高，在符合客观事实的基础上，考虑了数据变化规律及数据实际情况，赋权较为合理。

风险评估算法得到地理网格化风险评估值变化范围为 [0.0678, 0.7414]，风险值较高的网格样本普遍存在避雷器安装密度较低的问题。同时，风险评估为各项指标综合影响的结果。以广州南部某镇区域为例，此地区落雷活动强烈，以农田为主的走廊环境对线路无屏蔽作用，但此区域水系较多，土壤电阻率较小，因而即使处于落雷活动频繁地区，其雷击跳闸风险值并未达到较高水平。

根据公式计算所有3212条馈线雷击跳闸风险值，同时依据上文风险方法进行馈线雷击跳闸风险分级。以2017—2019年广州市10 kV公用线路雷击跳闸数据对馈线风险评估结果进行验证。如图4所示，线路雷击跳闸次数与其雷击跳闸评估风险值基本呈正相关关系。各风险等级评估结果验证如表3所示。

表3 馈线雷击跳闸风险评估结果验证Table 3 Verification of line lightning trip risk assessment results

图 4 馈线雷击跳闸风险评估结果验证Fig. 4 Verification of line lightning trip risk assessment results

各区段馈线数量随风险等级的降低而增多，符合针对性管理维护需求。2 0 1 7—2 0 1 9年130条一级风险馈线雷击跳闸比例达60.77%，单条馈线雷击跳闸最高次数达到9次，远高于其他风险等级馈线。评估结果展示的规律为：风险等级较高的馈线在雷击跳闸馈线比例、雷击跳闸总次数以及单条馈线最高雷击跳闸次数高于风险等级较低的馈线。表明了评估结果和分级方法的有效性。

5 结论

本文提出了一种基于配电网线路特点且低数据敏感性的大规模10 kV配电网线路雷害风险评估方法，得到如下具体结论。

（1）提出了10 kV配电网线路多维指标与雷击跳闸风险关联量化计算方法。其中，探究了线路走廊内建筑物密度、高度等要素与直击雷屏蔽效果的相关关系；引入了无失效Weibull模型在10 kV配电网线路绝缘子雷击故障风险的应用，解决了线路绝缘子因无监测数据、故障较少而评估困难的问题。

（2）根据配电网线路数据质量不够高的特点选取加权马氏距离型TOPSIS算法对线路雷击跳闸风险进行评估。结合AHP与熵权法对指标组合赋权，最终计算得出馈线的雷击跳闸风险，并根据数据分布特点对馈线雷击跳闸风险进行分级。解决了目前配电网监测手段匮乏情况下雷害风险评估困难的问题，有益于指导运行部门针对性地开展雷击跳闸防护工作。

（3）以广州市3212条10 kV架空线路为例进行雷害风险评估，并以2017—2019年历史跳闸数据对评估结果进行验证。风险等级较高的馈线在雷击跳闸馈线比例、雷击跳闸总次数以及单条馈线最高雷击跳闸次数高于风险等级较低的馈线，验证了评估结果的有效性。