基于HSA-PSO的配电网源-储协同优化控制方法

党彬，邹启群，张滨，付东，尤梦凯，乐健

(1. 国网安阳供电公司，河南 安阳 455000；2. 武汉大学 电气与自动化学院，湖北 武汉 430072)

0 引 言

随着光伏和风电等新能源发电的快速发展[1-3]，配电网结构日趋复杂，分布式电源(distributed generation, DG) 的接入势必会对电压质量和网损等指标带来新的挑战[4-7]。为确保配电网运行的安全性、经济性和可靠性，目前针对网损等问题主要采用无功优化的策略[8-10]；考虑到分布式电源及储能电池[11-13]的发展，多电源及储能系统(energy storage system, ESS)间有功优化配置将成为解决配电网网损等问题的有效手段。

文献[14]以分布式电源消纳最大化为目标，以电网安全稳定和公平调度为约束，提出多电源有功协调控制策略，并给出应用实例，但未考虑到储能电池的作用。文献[15]为解决高渗透率新能源并网后的电压越限问题，以电压总偏差最小为目标函数建立了配电网协调优化模型，采用基于分布熵的自适应粒子群算法来求解模型，但未考虑配电网网损。文献[16]提出一种考虑储能设备的协调控制策略，以电网功率波动最小为目标函数，采用改进粒子群算法求解，但未考虑网损指标。文献[17]基于分布式电源接入配电网有功功率波动、电压波动问题建立优化模型，使用快速非支配遗传算法求解，通过联合调度分布式储能系统提高电力系统稳定性，但未考虑网损因素。文献[18]基于有功网损最小和电压越限风险最小构建无功优化模型，采用非支配排序遗传算法对模型求解，实现光伏电源和储能系统的协调优化，但未考虑有功控制策略及分布式电源经济效益。文献[19]以网损最小为目标函数，采用改进粒子群算法对各节点分布式电源进行优化配置，但未考虑电压偏差等因素。

针对现有配电网多电源优化控制中优化目标单一的不足，本文提出考虑储能单元和分布式电源协同配合的配电网多目标优化控制策略，建立以配电网电压偏差最小、有功网损最小及分布式电源消纳量最大的配电网多目标优化控制模型，有效结合和声搜索算法(harmony search algorithm，HSA)和粒子群优化算法，提出了具有自适应能力的和声搜索-粒子群算法(HSA-PSO)对所建立的模型进行求解，通过仿真算例验证本文优化控制方法的有效性。

1 源-储协调的多目标优化控制模型

本文提出的源-储协调的配电网多目标优化控制模型通过对储能设备充放电、分布式电源以及常规机组出力的协调控制来实现配电网网损最小、节点电压偏差最小以及分布式电源消纳量最大的目标。控制方法以1 h为时段开展，全天共分为24个时段。

1.1 目标函数

1.1.1 节点电压偏差

本文采用如下指标来衡量配电网节点电压的偏差，即

式中：C1为节点电压偏差函数；i为节点编号；t为时段编号，若以1 h为1个时段，则全天分为24个时段；Ui,t为节点i第t个时段的实际电压；UN为配电网节点电压额定值。

1.1.2 配电网网损

分布式电源接入后会改变配电网潮流分布，合理规划各分布式电源出力能有效降低配电网网损。同时，考虑到储能系统状态转换过程中将产生功率损耗，配电网全天损耗为

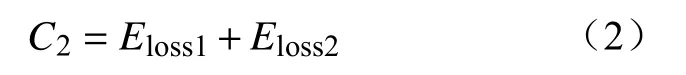
式中：C2为配电网全天总能量损耗；Eloss1为配电网全天能量损耗；Eloss2为储能系统全天能量损耗。

配电网全天能量损耗及储能系统全天能量损耗的计算方法为

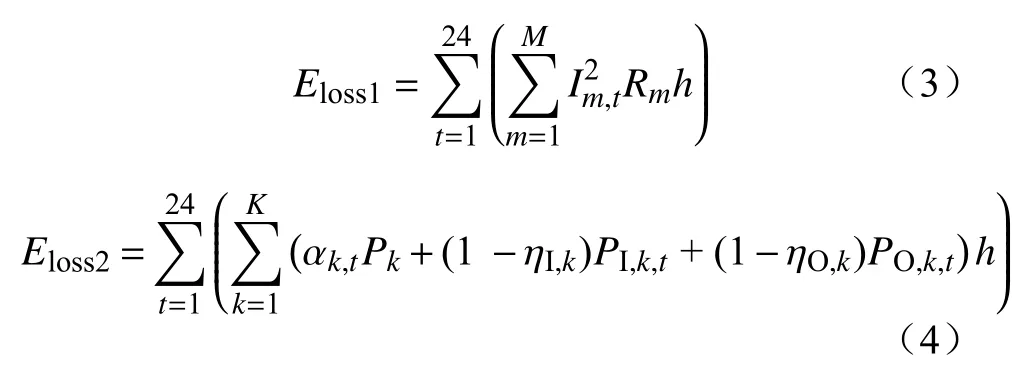
式中： M为配电网总支路数；Im,t为支路m第t个时段的电流有效值；Rm为支路m的电阻；h为1； K为接入的储能单元总数；αk,t为常数，用于表示储能单元k第t个时段是否发生充放电状态转换，发生转换时取1，否则取0；Pk为储能单元k状态转换能耗，一般为其容量的0.5%[20]；ηI,k、ηO,k分别为储能单元k恒定的充、放电效率；PI,k,t、PO,k,t分别为储能单元k在第t个时段充电、放电功率，且同一时间段至少有一个为0。

1.1.3 分布式电源出力消纳量

高渗透率分布式电源接入电网后，其出力的波动性和随机性增加了电网功率调节的负担，在出力无法完全消纳时需借助储能系统进行调节。本文采用如下指标计衡量分布式电源出力的消纳情况，即

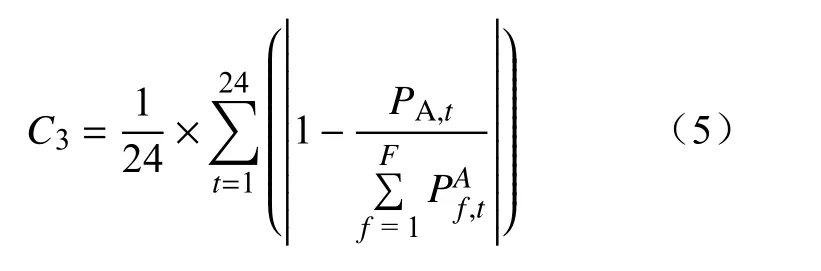
式中：C3为分布式电源消纳函数； F为分布式电源总个数；为分布式电源f第t个时段的实际输出功率；PA,t为系统第t个时段分布式电源出力最大消纳空间。

式中： H为配电网负荷总个数；PLe,t为负荷e第t个时段的功率； R为系统中除分布式电源外其他常规电源的数目；为常规机组b第t个时段的输出功率。

本文考虑的是配电网自身的供需平衡，认为与外部电网的功率交换为0。

1.1.4 综合目标函数

本文采用权重系数法将3个函数综合后构成单一目标函数[13]，即

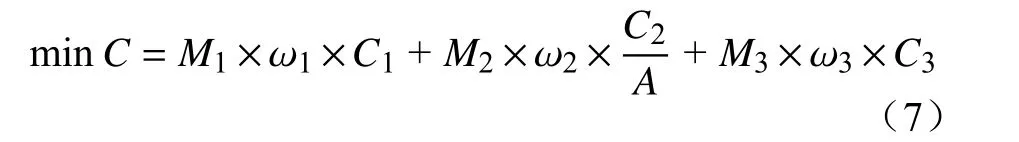
式中：ω1、ω2、ω3分别为3个子目标的权重系数，且ω1+ω2+ω3=1；A为不进行优化控制时的全天总能量损耗；M1、M2、M3分别为3个子目标函数的惩罚因子。

任一时段出现某个节点的电压、储能单元的荷电状态和分布式电源出力越限时，相应的惩罚因子都将增加，具体为

式中：Umin、Umax分别为允许的节点电压下限、上限，本文中分别取节点额定电压的0.95和1.05；Sk,t为储能单元k在第t时段的荷电状态；Smin、Smax分别为储能单元荷电状态最小、最大允许值；分别为分布式电源f出力的下限、上限。

1.2 约束条件

(1)功率平衡约束为

式中：D 为配电网节点个数；θij,t为第t个时段节点i、j间电压相角差；Gij、Bij分别为节点导纳矩阵元素Yij的实部和虚部；PDi,t为第t个时段节点i负荷的有功功率；为第t个时段节点i的电源注入功率。

式中：SESS,k为储能单元k的额定容量。

考虑储能单元的使用寿命，其荷电状态需满足如下约束，即

2 基于HSA-PSO的优化求解方法

2.1 HSA及PSO算法

和声搜索算法是一种源于音乐创作过程的全局优化算法。对于一个优化问题min Y，HSA算法的基本步骤如下。

(1)随机产生J个和声向量形成和声记忆库(harmony memory, HM)。和声向量对应于待优化目标函数Y的解向量，其维数L为优化问题决策变量的个数。

(2)产生一个新的和声向量(new harmony vector,NHV)。NHV的第d个元素xdNHV的计算公式为

(3)调整NHV中的各元素。NHV的第d个元素的更新公式为

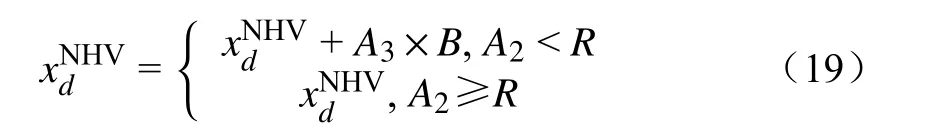
式中：B为微调带宽；A2和A3为0～1范围内的随机数；R为微调概率。

(4)更新HM。将对应NHV的函数值Y(V)与当前和声记忆库中的最大目标值Ymax进行比较，若Y(V)＜ Ymax，则用NHV替换Ymax所对应的和声向量；否则，舍弃NHV。

(5)循环执行步骤(2)～(4)，直至达到最大迭代次数，算法结束。

可以看到，HSA每次迭代中新和声矢量不完全从上代所有和声矢量中产生，具有良好的遍历性，可避免陷入局部最优[21-22]。受限于搜索机制，HSA每次更新没有方向性，需要迭代次数较多而且搜索速度较慢[23]。

粒子群优化算法(particle swarm optimization algorithm, PSO)是通过模拟鸟群觅食过程而提出的一种基于群体智能的全局搜索算法[24]。PSO算法多个粒子共存，每个粒子根据全局最优解和局部最优解在目标搜索空间中向更好的位置飞行，搜索最优解，收敛速度较快，后期容易陷入局部最优[25]。

2.2 HSA-PSO算法及其实现流程

本文考虑到HSA具有全局最优搜索能力的优势以及PSO收敛速度快且具有方向性的特点，提出了HSA-PSO算法进行优化问题的求解，将HM中的每个向量作为一个粒子，利用PSO更新HM。HSA-PSO算法具体实现步骤如下。

(1)以分布式电源、常规机组和储能单元充放电功率为决策变量并赋初值。随机生成J个和声向量构建初始HM。设定HSA-PSO算法中参数。

(2)确定个体最优解和全局最优解的初始值。各向量的初始值即为各向量的初始个体最优解。运行潮流计算程序，计算HM中各个和声对应的最小化目标函数C，最小目标值对应的和声向量即为全局最优解。

(3)利用PSO算法更新HM中各个和声向量的速度和位置。

(4)评价HM的每个和声向量，更新个体最优解和全局最优解。

(5)根据公式（18）和（19）创建NHV。

(6)评价NHV，将对应NHV的函数值C(V)与当前HM中的最大目标值Cmax进行比较，若C(V)＜Cmax，则用NHV替换Cmax所对应的和声向量；否则，舍弃NHV；然后更新全局最优解和单个最优解。

(7)迭代次数增加，如果迭代次数未达到最大值，则转到步骤(3)。否则，输出全局最优值。

3 仿真算例及分析

本文以某10 kV配电网为算例目标系统，具体接线布局如图1所示。

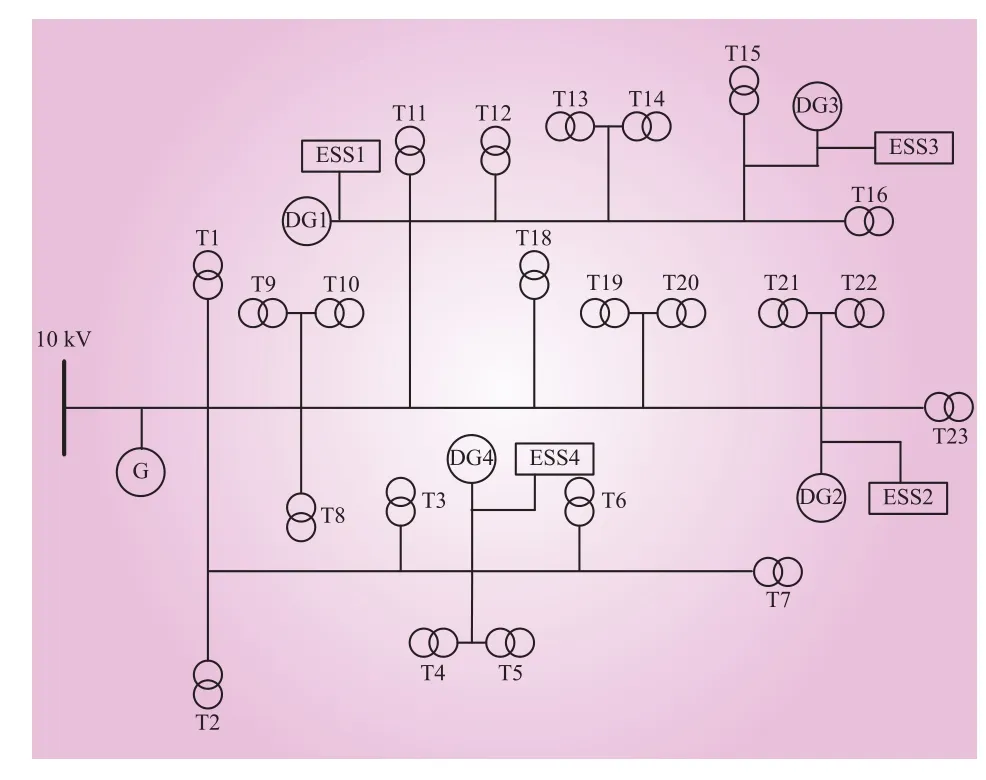
图1 某10 kV配电网Fig. 1 Diagram of a 10 kV distribution network

该配电网全长24.3 km，具有配电变压器23台，总容量5 105 kV·A。配电网接有1个常规燃气轮机和4个分布式电源，燃气轮机G输出功率上限250 kW。DG1和DG2为分别配备储能单元ESS1和 ESS2的光伏电源；DG3和DG4为分别配备储能单元ESS3和 ESS4的风电机组；各电源功率因数均为1。所有储能单元最大储存电量均为600 kW·h，输出功率上限均为100 kW。初始储能单元的荷电状态S为0.6，S最小、最大允许值分别取为0.1、0.9；充放电效率均取0.9。

本文以配电网全天网损最小为主要优化目标，结合专家调查权重法将子目标函数的权重系数 ω1、ω2、ω3分别确定为 0.3、0.4、0.3。优化算法中使用的参数J 、H 、R 、B分别设置为5、0.9、0.3、0.01。

分布式电源预测输出功率如图2所示，其可作为分布式电源相应时段内输出功率的上限。

图2 分布式电源预测功率Fig. 2 Forecasted output powers of DGs

分别采用传统PSO算法和本文提出的HSAPSO算法进行优化模型的求解，所得各分布式电源出力和储能单元充放电功率的对比，如图3所示。

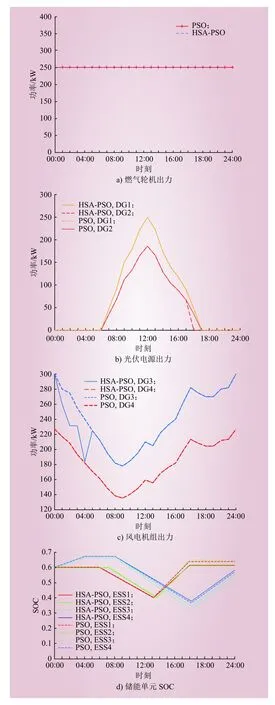
图3 不同优化算法的结果对比Fig. 3 Comparison of the results of different optimization algorithms

4个储能单元ESS1、ESS2、ESS3和ESS4当日24时的S在HSA-PSO算法优化下分别为0.610、0.615、0.550和0.580，在PSO算法优化下分别为0.635、0.645、0.525和0.570，表明各分布式电源当日总出力基本完全被消纳；同时HSAPSO算法优化结果相较于PSO算法优化结果更接近初始的0.6，表明HSA-PSO算法可更有效实现分布式电源完全消纳的目的，避免了陷入局部最优。

HSA-PSO算法下各节点电压全天分布如图4所示。由图4可知，各节点电压在一天各时间段内都保持较小的电压偏差，配电网整体电压质量较高；其中当日最大电压偏移发生在13:00的节点33上，降低至0.98，但仍满足节点电压的限值，表明本文方法有效实现了节点电压控制目标。

图4 HSA-PSO算法下各节点电压Fig. 4 Node voltages under HSA-PSO algorithm

配电网全天网络能量损失如图5所示。

图5 不同优化算法的网损Fig. 5 Comparison of network loss of different optimization algorithms

由图5不同优化算法的网损可知，在PSO算法和HSA-PSO算法优化下系统全天能量损耗分别为2 556 kW·h和1 472 kW·h，HSA-PSO算法优化结果相较于PSO算法优化结果减少42.41%，表明HSAPSO算法优化后各时段网损明显下降，优化结果更优于PSO算法。

4 结语

本文开展了源-储协调的配电网多目标优化控制方法的研究。综合考虑配电网电压质量、网损和新能源发电消纳，建立了分布式电源和储能单元优化控制的数学模型，并采用HSA-PSO算法进行模型求解，仿真分析结果表明：本文方法有效实现了配电网多时段网损的优化，降损效果相对PSO算法更为显著。各节点全天电压偏差均控制在较小范围内，具有较高电压质量。分布式电源发电量基本实现完全消纳，经济和环境效益明显。