悬链线方程在输电线路参数计算中的应用
2022-04-26吴春晖朱亦振
吴春晖,朱亦振,王 晓
(金华八达集团有限公司监理分公司,浙江 金华 321000)
0 引言
近年来,随着电网工程建设的高速发展,工程质量验收与输电线路的维护变得愈发重要。其中,输电线路自身的弧垂、线路两两交跨点间的交跨弧垂都是线路设计、施工建设和后期维护的重要指标[1]。线路弧垂是否在安全范围内直接影响输电系统能否安全、稳定地运行。弧垂过小,当遇到大风天气时,线路可能因受到的拉力过大而断线,进而导致危险事故发生;弧垂过大,则可能导致弧垂和地面物体接触,进而发生放电事故。因此出于输电线路及其周边环境的安全考虑,需要定期对输电线路各档的弧垂进行测量[3]。
已建成输电线路弧垂的测量通常由工作人员使用全站仪完成[4],这种方法虽然能够保证测量的精确度,但工作效率不尽人意,特别是在高山、湖泊、丛林、峡谷这些难以到达的目的地,测量任务无法完成。随着无人机的兴起,激光雷达测距逐渐投入弧垂测量作业中,但激光雷达存在造价高昂、易受天气因素影响的弊端,所以寻找一种快速、高效且成本较低的测量方法尤为重要[5]。
如今无人机技术日渐成熟,本文提出一种创新性的测量方案:利用无人机自身的空间定位功能,让其沿输电线路进行航点飞行,对线路轨迹进行拍照定位,传回空间位置坐标信息,随后用悬链线方程拟合线路轨迹,最终计算出线路弧垂、杆塔档距等参数。相较于利用全站仪人工测量,该方案在精度上稍逊一筹,但自动化程度更高,尤其是能解决人工无法到达区域的测量问题。相较于使用激光雷达测量,该方案建设成本更低。
1 悬链线模型拟合输电线路轨迹
1.1 输电线路轨迹模型的选取
通过理论分析可知,在对输电线路进行轨迹拟合时有2 种数学模型最相近,一种是抛物线公式,一种是悬链线公式。采用抛物线公式计算得到的线路弧垂往往偏小,并且随着参数的增大误差也会逐渐增大,不能满足日常监测的需要。相对而言,悬链线公式更适合沿线路轨迹的弧垂计算[6]。
悬链线公式如下[7-9]:

式中:以输电线路侧面为二维平面,海平面初始值为0,H为输电线路轨迹上的点离海平面的距离;t为输电线路轨迹上的点距离参考点的水平距离;A、B、C为常数,其值由悬链线方程通过3个航点测量值t计算得到,多组数据所得的A、B、C值不同时取均值。A决定悬链线开口方向以及大小,B决定偏移距离,A、C共同决定离海平面距离,三者共同决定悬链线形状。
当选取的参考坐标系以及初始参考点不同时,会导致A、B、C的取值不同,但计算弧垂以及其他相关参数时,最终的测量结果并不会发生变化。
1.2 模型空间坐标系的重建方案
1.2.1 地理坐标系与投影坐标系的简介
工程中使用GPS(全球定位系统),其地理坐标系包含经度、纬度和高程,因此得到的位置信息是基于WGS-84 标准的。而人们日常生活中所看到的坐标系是二维的,这种坐标系被称为投影坐标系[10]。
从三维坐标系变化到二维坐标系,必然会直接导致投影后的图像发生变形或失真,在不同的三维投影坐标系下可能会出现不同的失真,这就需要根据实际情况对其进行投影转换。常见的投影方法主要包括墨卡托投影法和等矩形投影法,其失真效果如图1 所示。对墨卡托投影坐标系而言,越到纬度高的地方,大小扭曲变形程度越大,所以墨卡托投影坐标系无法显示极地地区。

图1 墨卡托投影坐标系与等矩形投影坐标系失真效果
1.2.2 地理坐标系在伪墨卡托投影下的转换
本文提出的模型空间坐标系重建设计方案是将地理坐标系转换成伪墨卡托投影坐标系[11]。伪墨卡托投影坐标系去除了纬度在85.051 129°以上的南北两极区域,保证了其中一个正方形的独特性,从而使不同纬度和层次上的物体外形和形状保持固定不变,一个正方形可以接连不断地被划分成更多的小正方形来显示更多的细节。转换公式如式(2)—(3)所示:

式中:L1为GPS 中的经度;L2为GPS 中的纬度;x为空间坐标系中X轴数值;y为空间坐标系中Y轴数值。
1.2.3 建立新的空间坐标系
本文以从地理坐标系转换到伪墨卡托投影坐标系的x、y值为基础,再添加地理坐标系中的高度信息,将其作为z值,此外将其中一根杆塔所在位置定义为坐标原点,建立新的空间坐标系,如图2所示。
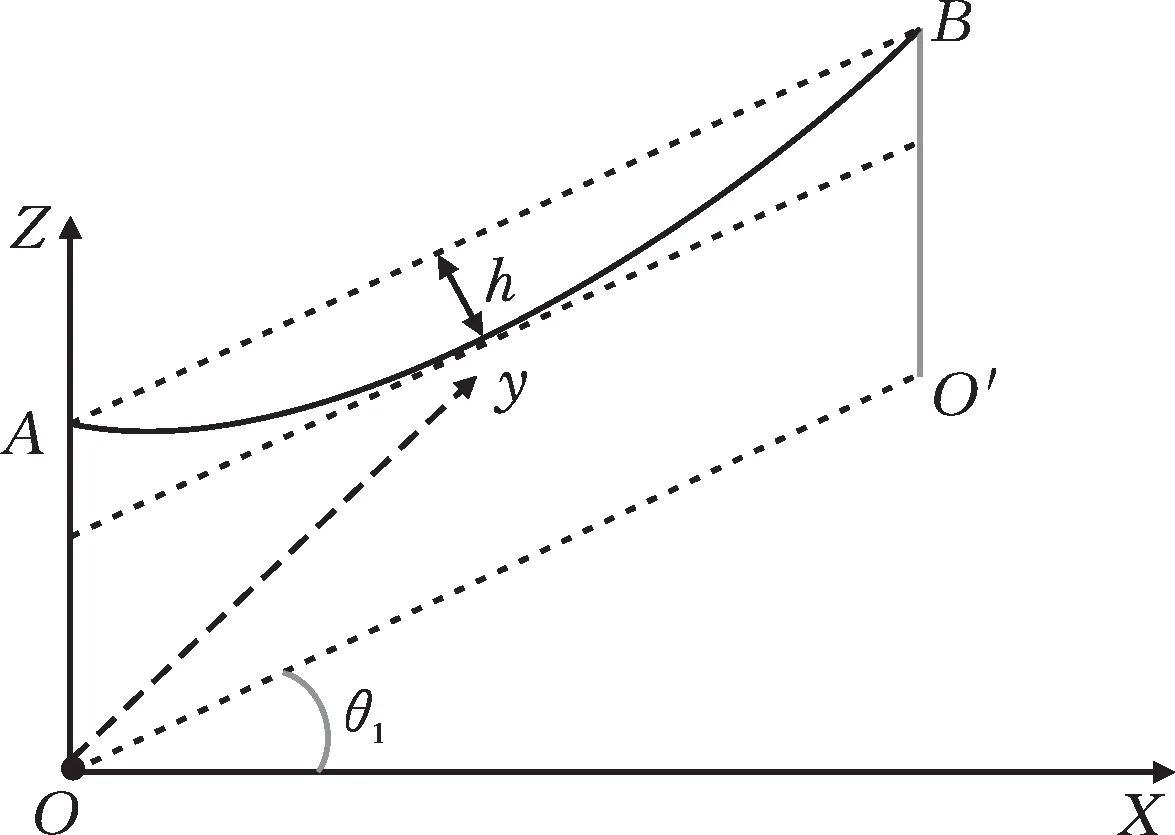
图2 新的空间坐标系
在新的坐标系中,杆塔OA与另一个杆塔O′B连接形成的直线结合其高度形成新的二维平面坐标系,如图3所示。
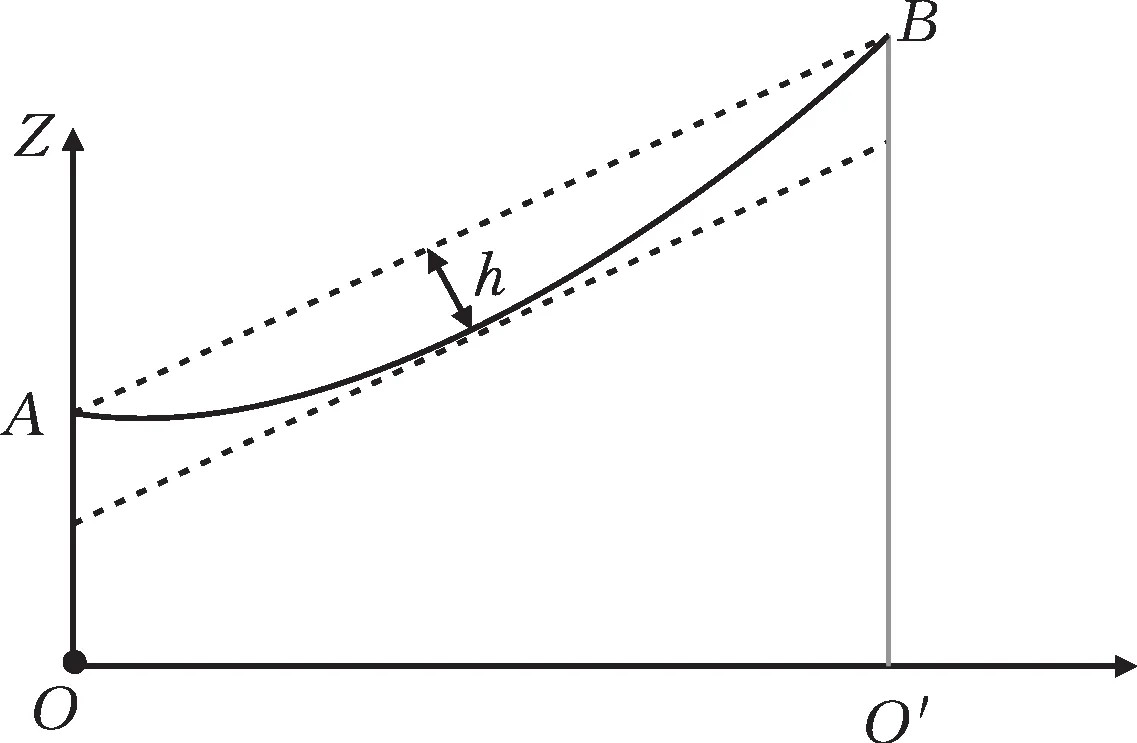
图3 输电线路侧面投影为新的二维坐标系
2 输电线路相关参数的计算方法
2.1 等高杆塔间输电线路的弧垂计算
等高杆塔中间输电线路的大致轨迹如图4 所示。图中,h1为输电线路最大弧垂,h2为输电线路最小离地高度,w1为杆塔之间的档距,H为杆塔位置的输电线路高度。
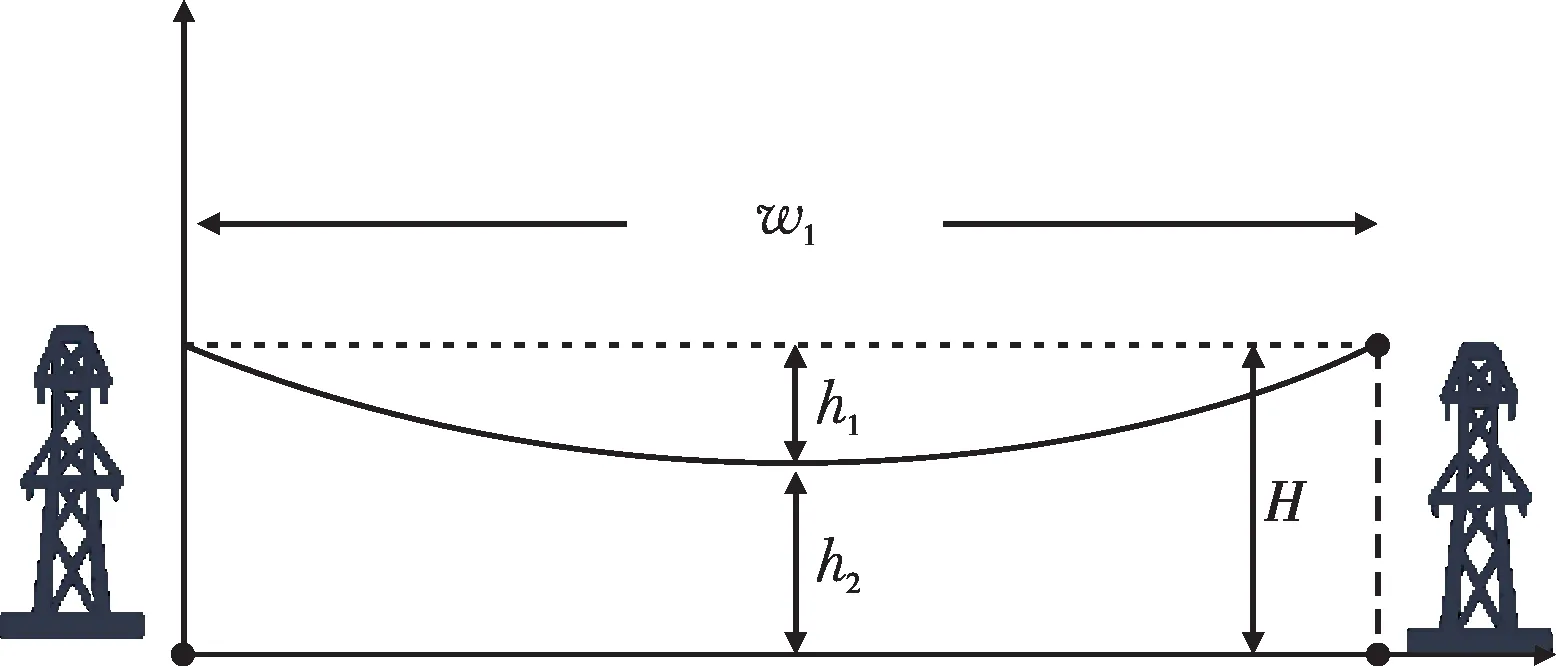
图4 等高输电线路轨迹
结合图2可知,当获取到输电线路轨迹上某点的经纬度信息,将其转换到新的空间坐标系后,可以推导出式(4)—(6)。
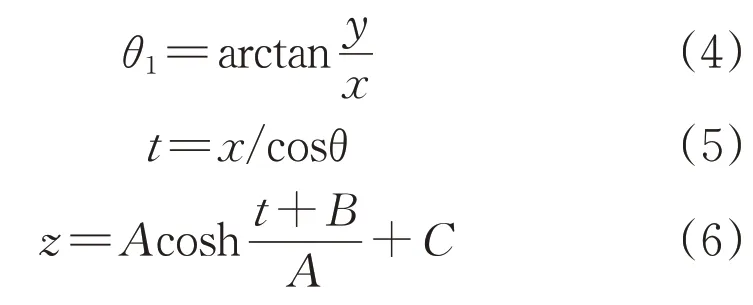
式中:θ1为杆塔所在直线与新空间坐标系中X轴所形成的夹角;y为式(3)中由纬度转换得到的值;x为式(3)中由经度转换得到的值;z为输电线路轨迹上的点通过悬链线公式拟合计算得到的高度值。
因为等高杆塔中间的输电线路轨迹所拟合的悬链线为对称图形(如图4所示),那么最大弧垂位置即在两杆塔之间的中心位置。将中心位置所对应的t值代入式(6)即可得到输电线路轨迹在空间坐标系中的高度值z,再利用无人机在杆塔位置获取的输电线路高度H减去z,就得到该等高输电线路的最大弧垂。通过无人机记录的杆塔位置信息,转换到空间坐标系后,也可计算出两杆塔之间的档距w1。最小离地弧垂值h2可以通过H-h1得到。
等高杆塔还存在非等高地形的情况,如图5所示。图中,H1为杆塔a位置的输电线路离地高度,H2为杆塔b位置输电线路离地高度,θ2为坡度。
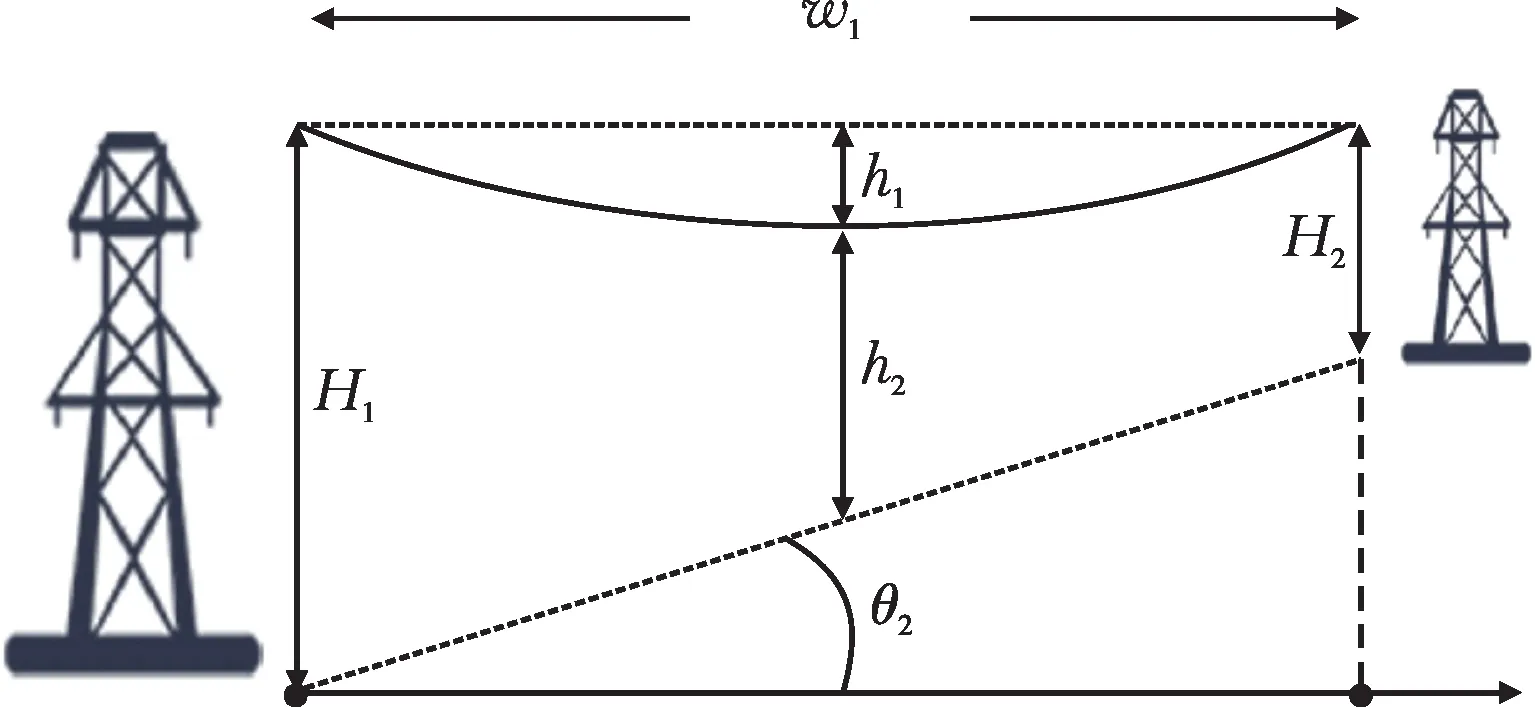
图5 等高输电线路非等高地形
此种类型的输电线路最大弧垂、两杆塔之间的档距均与前文计算方法一致。输电线路离地高度可根据坡度来计算。
2.2 非等高杆塔间输电线路的弧垂计算
非等高杆塔中间输电线路的轨迹大致如图6所示。图中,杆塔a所在输电线路离地高度为H1,杆塔b所在输电线路离地高度为H2,θ3为最大弧垂所在点的切线斜率所对应的角度,w1为杆塔之间的档距,h1为输电线路最大弧垂。
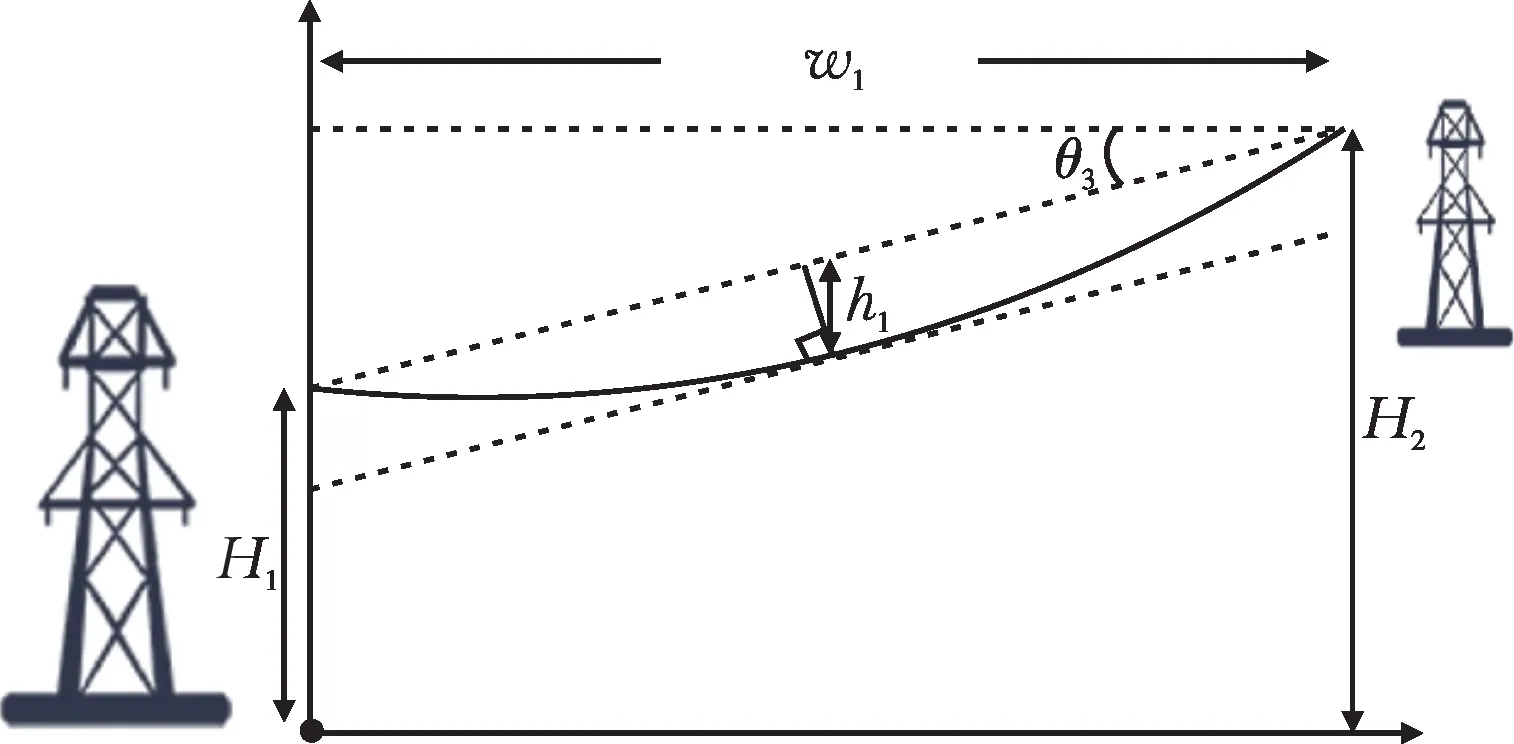
图6 非等高输电线路
若要计算h1,首先利用式(7)计算得出θ3:
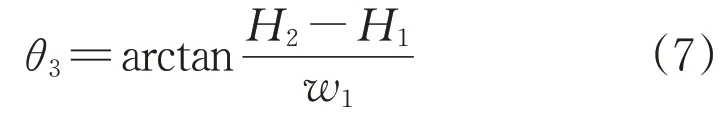
其中双曲余弦的求导公式为:
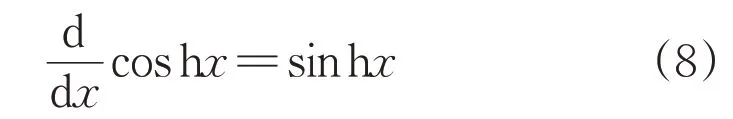
则悬链线的求导公式如下:
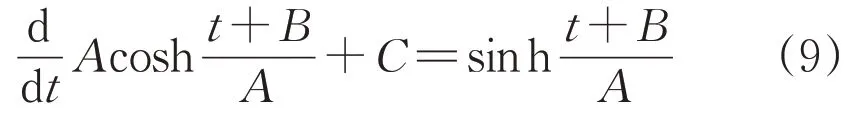
将θ3对应的斜率带入悬链线的求导公式中,通过式(10)算出最大弧垂所对应的t值。

将利用式(10)算出的t代入杆塔两端输电线路源头所连接形成的直线方程中,即图6中输电线路轨迹上方的虚直线,可计算出一个高度值ht,再利用式(11)可计算得到最大弧垂h1:

2.3 输电线路交跨位置的高度差计算
输电线路的交跨示意图如图7所示。如果2条交跨线路间的弧垂设计不当,同样会引发事故,所以监测交跨位置点的弧垂高度差也是电力巡检的重要任务。

图7 输电线路的交跨示意图
图7中,Sag为杆塔A1A2和杆塔B1B2交跨位置点的弧垂高度差。首先找到Sag对应输电线路所在位置的t值;再将输电线路轨迹在新建空间坐标系中以俯视图投影到平面坐标系,如图8所示;在平面坐标系中,可以得到杆塔A1A2和杆塔B1B2所在的直线方程,求解联立方程式(12),便可得出交跨点位置(x,y)。

根据投影坐标系的特点,将x值转换得到其对应悬链线投影上的值t,将t1、t2代入悬链线方程中,得到各自在交跨点的弧垂点离地高度,再相减就可以得到输电线路中交跨位置的高度差。
2.4 输电线路与树木等障碍物的交跨距离
输电线路与树木等障碍的交跨示意图如图8所示。
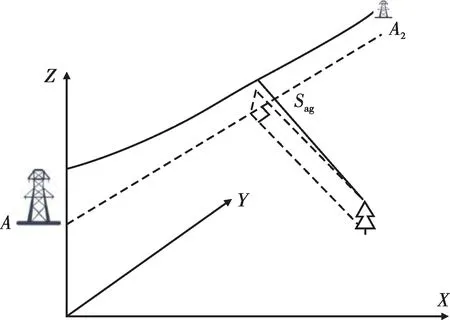
图8 输电线路与树木等障碍的交跨示意图
先确定从GPS 到新建空间坐标系中的(x,y),再通过x计算得到对应的t值,代入悬链线方程得到悬链线轨迹上交跨点位置对应的弧垂离地高度h1,(x,y)离悬链线投影距离d可由式(13)得到。
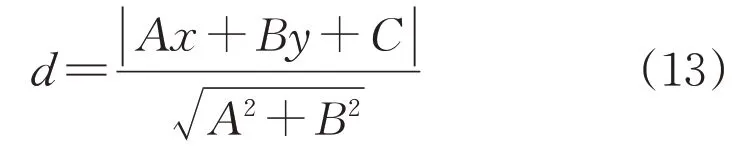
交跨距离可由式(14)计算得到。
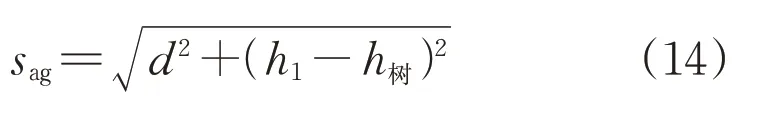
3 输电线路参数计算系统
3.1 巡线方案设计
在以往研究成果[12-13]的基础上,本文提出输电线路参数计算方案如下:基于无人机自身GPS 定位功能,飞手控制无人机从杆塔A位置沿线路轨迹飞行,记录经度、纬度、高度信息,并将上述信息传入线路参数计算系统中,系统拟合该线路的数学模型,利用数学模型计算得出相应参数。
在无人机作业过程中,飞手控制无人机始终和输电线路保持平行,所采集到的数据实际上是待测线路在空间上的平移,这种平移在计算弧垂时不会造成测量误差。并且目前行业级的无人机自身基于RTK模块可以达到较高的定位精度。因此,通过用无人机飞行轨迹从空间平移的角度来模拟输电线路轨迹的方式在理论上是可行的。图9为无人机描点方式的三维示意图。
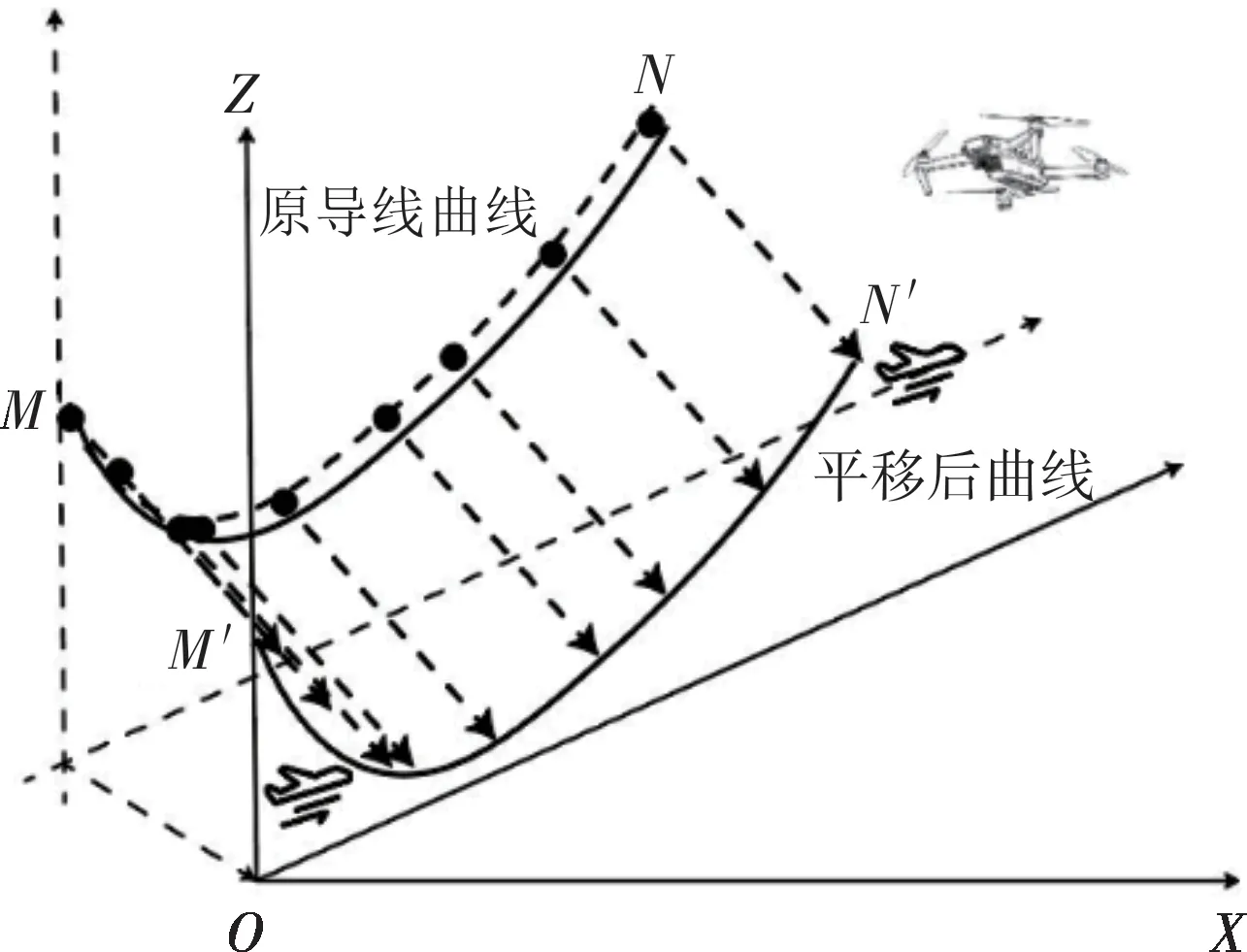
图9 无人机描点方式的三维示意图
3.2 系统误差分析
为了测试系统误差,工作人员利用全站仪采集输电线路弧垂和交跨处的弧垂高度差等数据。因为杆塔之间的档距由经纬度之间转换得到,对无人机没有直接影响,所以不必分析其误差。
在无人机测量输电线路交跨轨迹时,会因为无人机偏移而造成测量误差[3]。根据实际情况,发现该尺度远远小于地球尺度,故提出一种更为简便的调整误差的计算方法。在调整偏移误差时,可以投影到平面坐标系计算,具体如图10所示。
图10 中,AB点为线路交跨点,图中虚线所示为无人机飞行轨迹,所形成的交跨点为A′B′点。在该点得到的弧垂分别为AB′、A′B点对应的弧垂,这样就会有测量上的误差,对此需要根据无人机相对输电线路的飞行方式作出误差矫正。
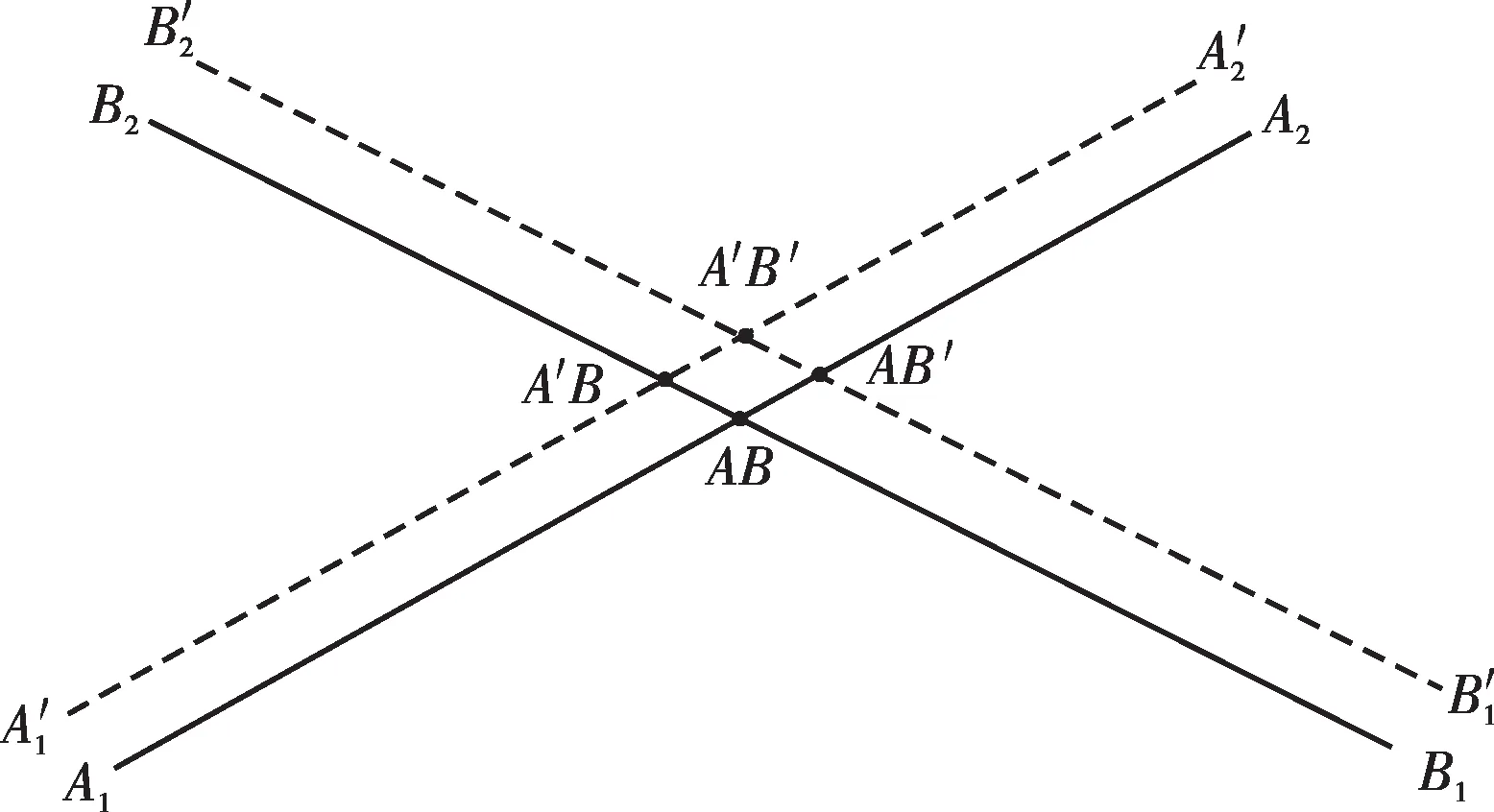
图10 误差轨迹俯视图
同理,如图11、12 所示,树木等障碍物与导线的交跨距离也存在误差。
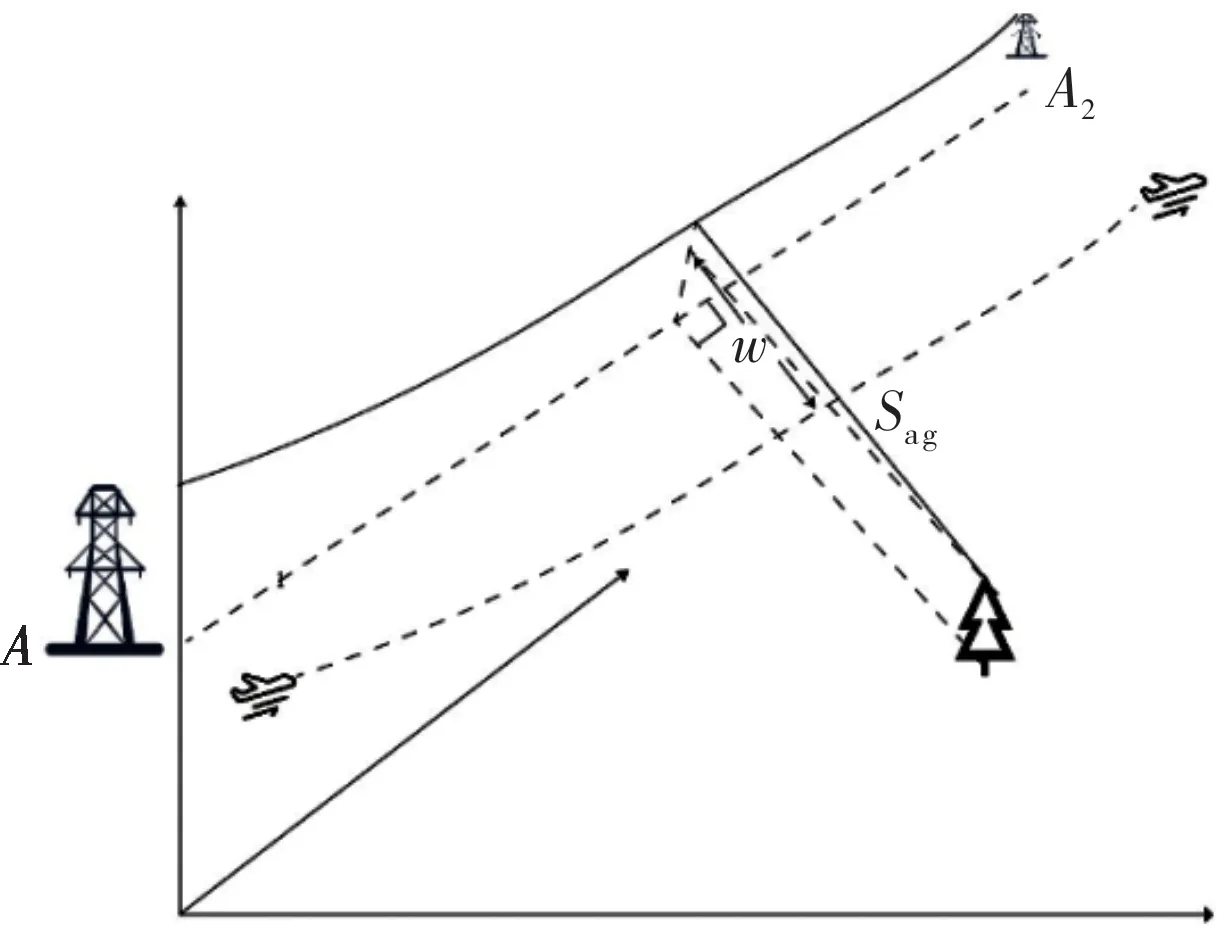
图11 无人机位于障碍物与输电线路之间时的误差
3.3 误差矫正
采用式(15)对图10所示交跨误差进行矫正:
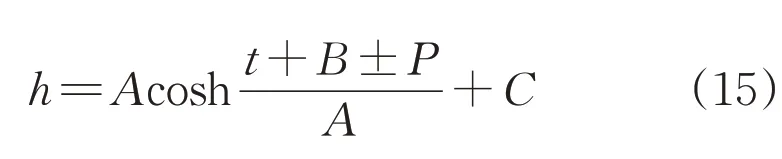
式中:P为无人机与输电线路实际位置的偏移值,根据无人机在输电线路侧边方向不同取正负值。
采用式(16)对图11所示交跨误差进行矫正:
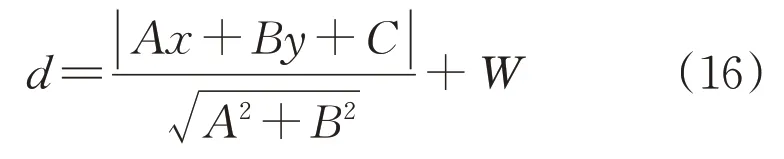
式中:W为无人机距离输电线路水平偏移距离。将式(16)代入式(14)可得交跨距离。
采用式(17)对图12所示交跨误差进行矫正:
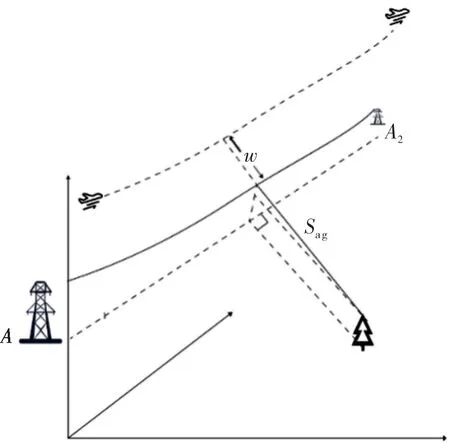
图12 无人机位于输电线路和障碍物同侧时的误差
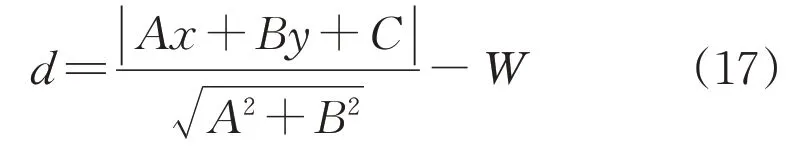
将式(17)代入式(14)可得交跨距离。
3.4 结果分析
本系统对采集的数据进行转换计算,并将其与全站仪测得的数据进行对比,结果如表1—7所示。

表1 各类数据说明
通过对表中误差进行分析,可知本系统的误差主要来源于以下4个方面。
1)悬链线方程包含3个未知量,用3点即可拟合出一条悬链线。本系统在用悬链线拟合输电线路轨迹时只使用了3个点的坐标,在实际作业场景中,输电线路轨迹并不一定完全符合悬链线公式,因此可以扫描多点,进行多次拟合,最后取均值,减少误差。
2)飞手在操控无人机进行打点定位时,与输电线路间的距离并不稳定,存在作业操作上的人为误差,与系统无关。
3)表7中,第1、2组计算数据与测量数据误差为3.759%,第3、4组误差为0.365 5%,第5、6组误差为0.806 16%,第7、8 组误差为0.658 58%。这是由于第1、2 组数据采用5 个点拟合悬链线所在直线,变换到新的坐标系下产生误差较大,其余数据直接使用两点计算直线,误差较小。与以往研究[15]对比发现,本文提出的计算方案精度处于一个较高水平。

表2 作业中获取的各类数据
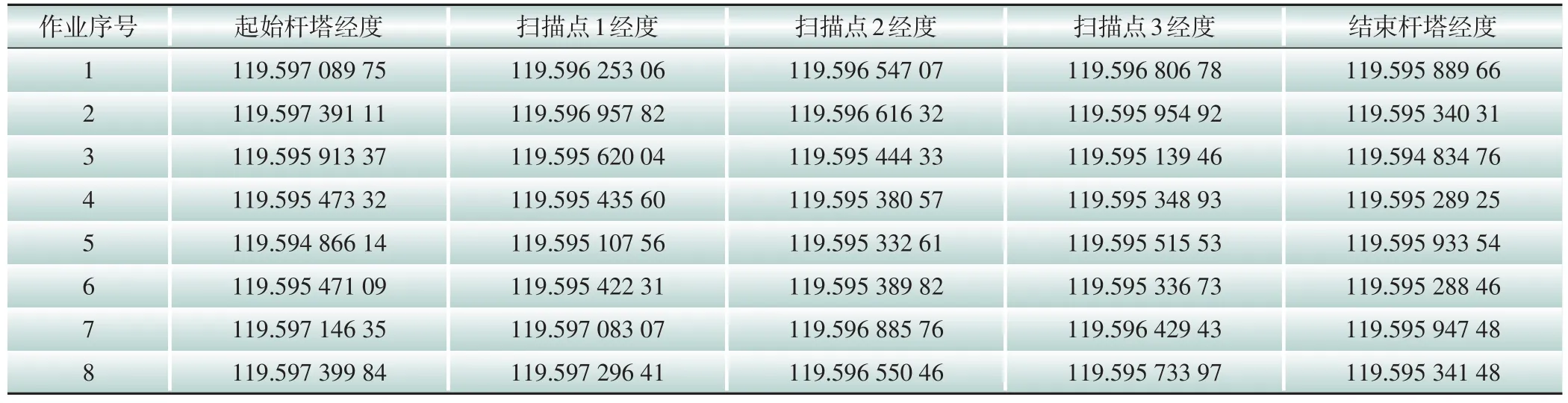
表3 作业中获取的杆塔之间扫描点经度数据(°)
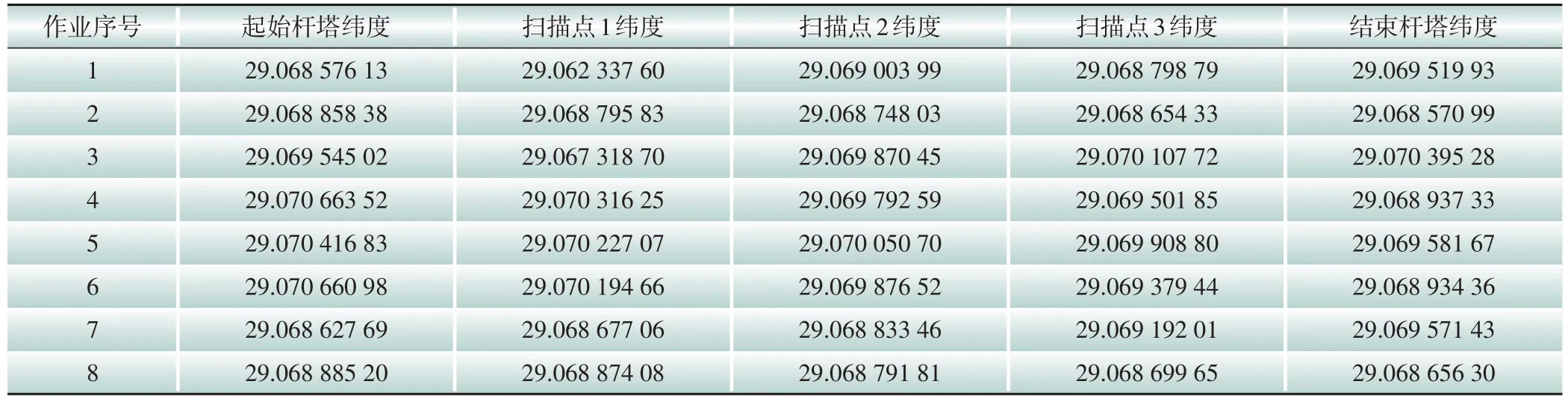
表4 作业中获取的杆塔之间扫描点纬度数据(°)

表5 作业中获取的杆塔之间扫描点高度数据m

表6 系统计算数据与实测数据
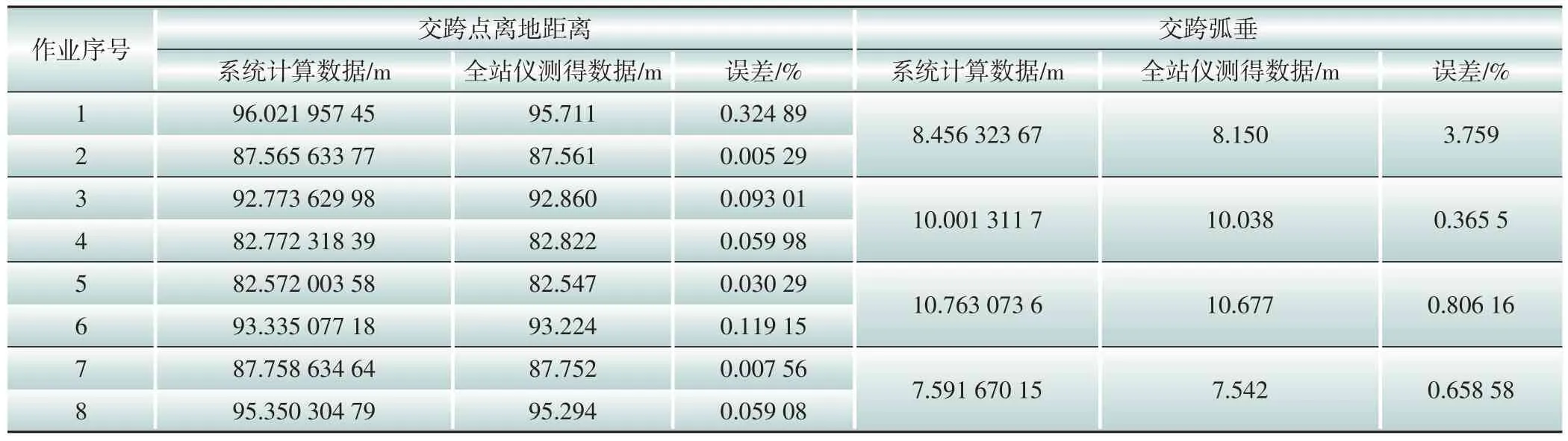
表7 数据误差分析
4)无人机在对输电线路进行打点定位时,由于天气原因输电线路并不是固定不动的,所以也会存在误差。
4 结语
本文提出的基于悬链线方程的输电线路参数计算系统,能够在误差允许范围内较快计算出输电线路的弧垂、交跨点弧垂高度差和杆塔档距,并且完成工程应用。相较于以往方案,本方案在数据采集时具有较高的时效性,并且作业成本较低,只需一台小型无人机即可完成整套操作,能够到达山林、河流、密林等人力难以到达的地方进行测量,显著提高了作业效率。此外,本文所提方案所需参数更少,计算速度更快,计算结果误差小。因此,本文提出的输电线路参数计算系统在线路巡检和维护中具有较高的工程应用价值。
