总纵弯曲下舰船上层建筑结构强度钢模试验

2022-04-26刘俊杰丁震马琳卞鑫李政杰

中国舰船研究 2022年2期

刘俊杰，丁震，马琳，卞鑫，李政杰

1 中国船舶科学研究中心，江苏无锡 214082

2 中国舰船研究设计中心，上海 201108

0 引言

作为大型舰船驾驶室、指挥室、舰员住舱等重要场所的“提供者”，上层建筑的结构强度关系到舰船的结构安全和作战能力。上层建筑的结构强度主要关注其参与舰船总纵弯曲时的承载能力，是造船界长期以来一直关注的问题。由于舰船主船体结构在纵向上呈连续分布，故通常采用船体梁理论来计算船体结构的总纵强度[1]，但由于上层建筑通常短于船长，构成了船体结构上的不连续性，因而会产生明显的应力集中现象。Crawford 提出了双梁理论，即假定主船体和上层建筑分别以单独梁的形式存在，并各自承受水平力和垂向力，然后基于以上假设计算出2 个梁的正应力、挠度及曲率[2]。Pei 等[3]基于双梁理论分析了某内河客船主船体与上层建筑结构的相互作用，并对上层建筑参与总纵弯曲的有效度进行了研究。钱仍勣[4]提出了一种评估上层建筑有效度的简化模型，其把船体的三维结构简化为二维模型，较好地模拟了上层建筑与主甲板结构间的相互作用，简化了上层建筑参与船体总纵弯曲程度的计算。何祖平等[5]采用有限元手段对某型舰船上层建筑端部产生的应力集中现象予以了分析，并对其应力集中系数进行了计算。

国内有些学者同样采用有限元方法研究了上层建筑的结构强度以及其对船体总强度的影响[6-8]。采用有限元方法能够模拟船体结构的几何形状，并对上层建筑结构在理想受力状态下的应力分布进行高效计算，但无法直观地反映典型部位结构在受载状态下的应力响应和变形特征，因此有必要开展相应的试验，对结构应力分布特征进行研究。李永宽[9]针对复合材料上层建筑的结构强度开展了模型试验研究，但试验采取的是舱室截断模型，导致模型边界条件及载荷加载方式较难模拟。

基于此，本文将以某舰艏楼上层建筑为研究对象，对其在船体承受中拱总纵弯矩时典型部位的结构响应开展大尺度模型试验，通过对试验结果的分析，为该舰结构优化设计提供支撑。

1 模型相似关系与结构简化

1.1 模型相似关系

本文模型试验的主要目的是研究上层建筑结构在总纵弯曲下的应力分布特征，因此，试验模型在结构上应满足几何相似，另外为了评估实船所受弯矩，要求试验载荷满足相似性准则。为了确保通过模型试验可以得到与实船相应载荷工况下相同的应力水平，试验模型应使用与实船相同的材料。描述材料特性的基本物理量包括杨氏模量E、剪切模量G和泊松比µ，通常，选择E和µ这2 个独立的物理量来描述结构的材料特性。

船体结构属箱型梁类薄壁结构，因船体结构尺度与船体板的板厚量级不同，所以在采用缩尺模型开展钢结构强度试验时，不可能完全满足几何相似性，可以采用不同的缩尺比。为了尽量减小尺度效应对试验结果的影响，本文试验模型采用大尺度钢质模型，采用的缩尺比为：主尺度缩尺比 λL=1∶4，板厚缩尺比 λt=1∶2。结构弯曲正应力的计算公式为 σ=Mz/I，对于船体总纵弯曲，M为船体横剖面上的垂向弯矩，z为上层建筑待求应力点距中和轴的距离，I为横截面对中和轴的垂向惯性矩。根据相似性理论，可以得到模型和实船同一站位剖面特性的相似关系为

式中：Im和Is分别为模型和实船的剖面垂向惯性矩；znm和zns分别为模型和实船的垂向中和轴高度。

为了满足总纵弯曲下相同位置处产生的应力相等，模型试验施加的弯矩Mm和实船对应的弯矩Ms应满足如下相似条件：

1.2 结构简化

本文试验选取包含艏楼上层建筑在内的船体舱段作为试验模型设计对象，但该舱段范围内的主船体较高，若按前文给出的主尺度缩尺比，模型高度偏高，并且因主船体内部构件种类繁多，不仅会显著增加模型加工成本，而且还会给模型的运装带来困难。考虑到模型试验的主要目的是研究上层建筑的应力分布，因此，有必要对主船体结构进行简化。为了不影响上层建筑结构在总纵弯矩作用下剖面应力的分布特征，需保证简化船体结构的剖面特性与实船相似。采用箱型梁代替主船体，箱型梁的上表面为船体主甲板，主甲板之上的上层建筑完全保留，所有船体构件均根据实船尺度和板厚并按上述缩尺比进行缩尺，其中某些纵骨按给定的板厚缩尺比缩尺后若其钢板板厚在市场上无法直接采购，可采用相近厚度的钢板制作，通过调整纵骨尺度，来使调整后的纵骨横截面积与缩尺后的纵骨横截面积相等，这样，可保证船体垂向弯矩下的甲板结构响应与真实状态基本相同。根据船体总纵弯曲应力计算公式σx=Mz/Iy，为了保证上层建筑的应力分布特征与实船相同，应当同时保证简化结构的上层建筑距中和轴的距离z及剖面惯性矩Iy与实船相同。主甲板以下的船体结构简化方法为：以目标船船体舱段的多个典型剖面为基准，采用长方形箱型梁代替主船体，不必完全遵循上述缩尺原则，箱型梁的高度取为8.5 m（缩尺后为2.215 m），宽度与主甲板相同。通过调整箱型梁舷侧和底板板厚，并在舷侧和底部上布置扁钢与T 型钢扶强材，同时对扶强材的尺度和板厚进行调整，可以满足上述约束条件。简化前、后相同肋位处的剖面结构如图1 所示。

图1 主船体等效简化前、后结构对比图Fig. 1 Comparison of main hull structure before and after equivalent simplification

2 试验模型与加载方法

根据试验对施加载荷的需求，以及实验室加载设备自身能力和设备位置的需求，将采用四点弯曲加载方法。该目标船艏部整个上层建筑的长度为29.5 m，试验选取包含该段上层建筑的船体舱段作为试验段，该舱段的实船长度为35 m，最大船宽16.33 m，最大高度14.8 m。根据目标船的实船结构并按照上述模型缩尺比和结构等效简化方法，设计的试验段钢质模型长8.75 m，最大宽度4.08 m，最大高度3.64 m；为了能够在模型试验段内得到相应的纯弯载荷，模型两端各设计了3 m长的加载段；同时，为了使试验段两端结构应力响应不受试验所施加集中载荷的影响，在试验段和加载段之间设置了过渡段模型。根据计算，加载段取2.375 m 既可满足试验精度要求，又能满足试验设备位置要求。图2 所示为模型整体分段示意图（图中数值的单位为mm）。过渡段和加载段两端对称分布，模型总长20 m，从一端到另一端的尺度为0.25 m（两端载荷施加处局部加强）+3 m（加载段）+2.375 m（过渡段）+8.75 m（试验段）+2.375 m（过渡段）+3 m（加载段）+0.25 m（两端载荷施加处局部加强）。模型试验段的钢质材料与实船相同，其名义屈服强度 σs=315 MPa，过渡段和加载段采用屈服强度 σs=345 MPa的钢材制作，整个试验模型总重约49 t。

图2 试验模型整体分布Fig. 2 The distribution of whole test model

本模型试验采用如图3 所示的加载系统，包括加载装置和固定装置2 部分。其中，加载装置分为接触装置、加载梁和油压推缸3 个部分，接触装置同加载梁配合使用，油压推缸通过加载梁和接触装置将载荷传递给模型；固定装置由反力架、反力梁和接触装置组成，其中反力梁主要是为了防止模型在极限加载工况下模型两端发生大变形，其对模型起简支作用。因本模型试验载荷不会导致模型发生大变形，因此没有采用反力梁。由于本试验模型自身质量较大，为了避免模型重力对结构应力测量的影响，采用将模型平躺放置的方法（船体右舷舷侧面对地面），并在主船体与地面之间采用滑轮进行支撑以减小两者之间的摩擦力，然后在模型底部（船底）加载，模拟纯弯载荷下船体中拱状态下的上层建筑结构响应，如图4 所示。

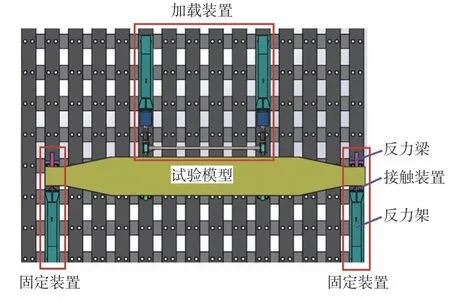
图3 试验加载系统Fig. 3 Test loading system

图4 试验前的模型Fig. 4 Model state before test

3 试验测量及数据处理方法

根据试验目的，采用应变片对上层建筑典型部位在中拱弯矩下的结构响应进行测量。测点位置主要依据该船有限元计算结果选取，并布置于高应力及典型位置处，包括上层建筑前后壁开口角隅及上层建筑根部（图5（a））、上层建筑各层甲板开口角隅及典型位置（图5（b））、上层建筑侧壁开口角隅、典型位置及与船体主甲板连接的圆弧过渡段（图5（c））等位置。本文试验共布置了72 个应变测点，其中三向应变测点15 个，测点编号以“S”开头；单向应变测点57 个，测点编号以“A”开口，图5 给出了部分测点的位置。

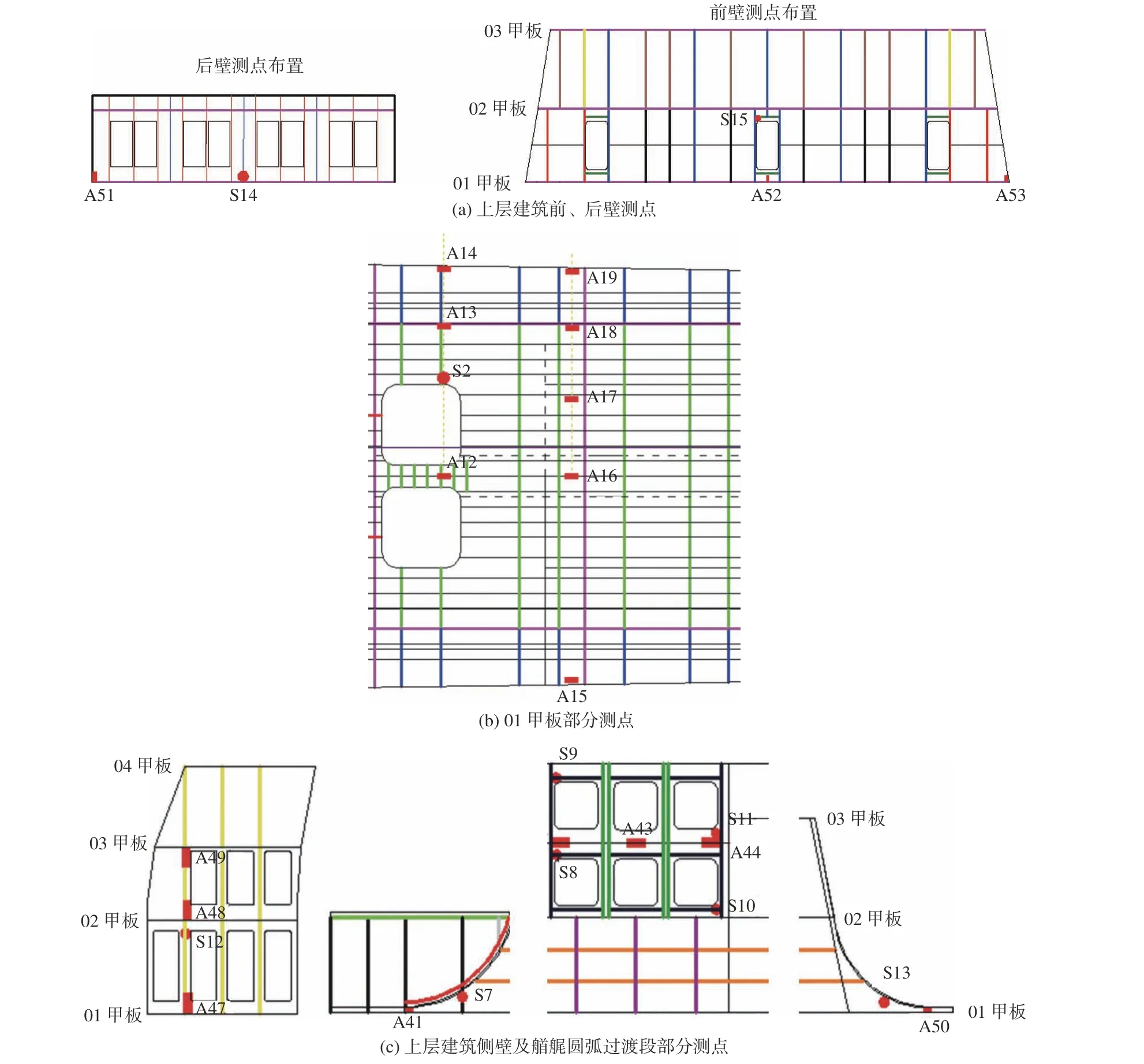
图5 部分测点Fig. 5 Parts of the test points

通过试验可以直接测得各测点处的应变值，若要对上层建筑结构的应力响应特点进行分析，需将应变值转换为应力值。试验中，有些测点使用的是单向应变片，例如主应力方向较为明确的上层建筑与船体主甲板连接处（主应力方向为垂向）；有些测点使用的是三向应变片，例如开口角隅处。对于单向应变片，根据胡克定律可以计算对应测点的应力值为

对于三向应变片测得的应变值，需通过以下公式计算其测点处的von Mises 等效应力。三向应变片的纵向、横向和剪切应变 εx， εy， γxy可以表示为：

式中，ε0°，ε45°，ε90°分别为测量得到的0°，45°和90°处的正应变。对应的纵向、横向和剪切应力σx， σy， τxy可以表示为：

三向应变片测点处的主应力可以表示为：

三向应变片测点处的von Mises 等效应力 σe为

或

4 试验结果分析

4.1 上层建筑结构应力集中现象分析

在中拱弯曲载荷下，上层建筑应力最大值出现在靠近艉端的侧壁开口角隅测点S12（三向片）处，该测点位于目标船上层建筑左舷烟囱侧壁尾部向前第2 个开口上角隅垂向切线处（图5（c）和图6），在试验载荷（即单个油缸推力）达到263.6 t时，该测点的von Mises 等效应力达356.6 MPa（图7），已经超过材料的名义屈服应力。由图7可以发现，当试验载荷约为125 t时，该测点处的应力变化曲线发生了明显的非线性变化，且其他某些测点也有类似的现象，只是该现象出现时的试验载荷值有区别。经观察，这种现象均发生在靠近焊缝位置的测点处，产生这种现象的原因可能是由于测点离焊缝较近，当达到一定的试验载荷，在进行焊接施工时焊缝附近的残余应力释放对测点处的结构应力产生了影响。

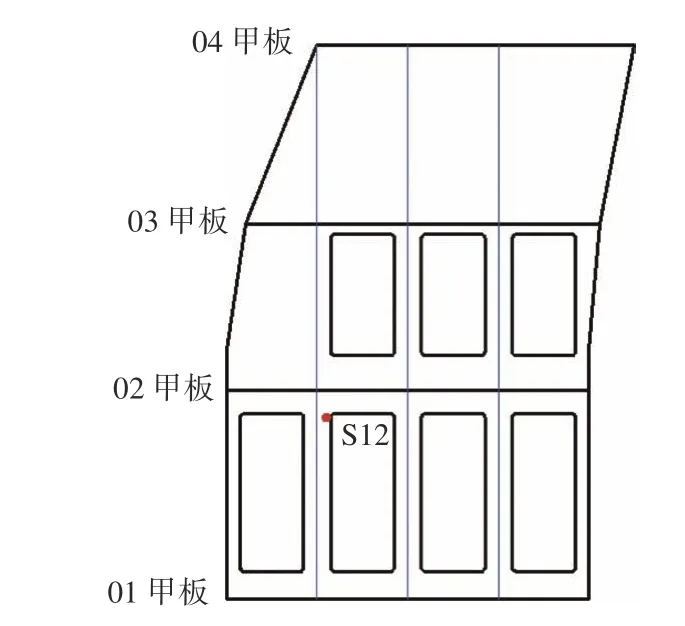
图6 测点S12 位置Fig. 6 Location of test point S12

图7 测点S12 处von Mises 等效应力随载荷变化图Fig. 7 Variation of von Mises equivalent stress with load at test point S12

图8 给出了试验载荷为263.6 t 时的有限元计算结果。从中可以看出，上层建筑最大应力出现的位置与试验结果相同，有限元计算结果为345 MPa，与试验结果间的偏差为3.25%。该船上层建筑侧壁开口群的高应力主要集中在主甲板与02 甲板之间的开口角隅处，应力集中现象较为严重，因此需对该处结构进行局部加强或优化设计。

图8 上层建筑侧壁开口群结构有限元计算结果Fig. 8 FE calculation results of superstructure sidewall openings

由试验结果分析还发现，在上层建筑侧壁与主甲板连接的过渡圆弧上，也存在明显的应力集中现象。图9 给出了艏部和艉部圆弧过渡段测点的von Mises 等效应力变化曲线。从中可以看出，艏、艉圆弧过渡段测点处的应力值相差不大，当达到试验指定的载荷时，艏部测点处的应力略大于艉部，艏部测点S13 处的应力为118.87 MPa，艉部测点S7 处的应力为111.0 MPa。有限元计算结果如图10 所示。从中可以看出，有限元计算结果与模型试验得到的艏、艉应力集中点的对比结果是相同的，应力值都是艏部大于艉部，由模型试验得到的数值结果低于有限元计算结果。产生这种现象的原因是，因圆弧过渡段腹板与面板焊接处存在焊缝，影响了测点的布置，从而导致测点距圆弧边缘存在间距，故未能测到应力集中点处的最大应力值。

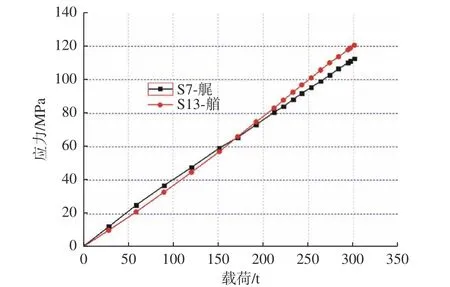
图9 上层建筑侧壁与主甲板连接圆弧过渡段测点等效应力变化曲线Fig. 9 Equivalent stress at test points of round transition structure between the superstructure sidewall and main deck

图10 上层建筑与主甲板连接圆弧过渡段有限元计算结果Fig. 10 FE calculation results of round transition structure between the superstructure sidewall and main deck

4.2 上层建筑参与总纵弯曲的有效度分析

根据文献[10]，给出上层建筑参与船体总纵弯曲的有效度 η的计算公式为

式中： σ0为不考虑上层建筑时主甲板的应力，MPa； σp为船体主甲板的实际计算应力值，MPa；σ100为上层建筑100% 有效时的主甲板应力，MPa。本文采用试验对象中船体舱段上层建筑的中间肋位剖面来计算上层建筑的有效度。根据公式σx=Mz/Iy，在计算 σ0时，将上层建筑（主甲板以上的结构）去掉，也即仅剩主船体部分，对应于上述剖面，计算剖面的垂向惯性矩Iy主船体及中和轴高度Zn主船体，由此得到主甲板距离中和轴的垂向距离为Z1，垂向弯矩则取对应试验载荷时的弯矩值，采用理论计算方法，求得 σ0=79.4 MPa； σp采用试验测得的主甲板上对应于横剖面与中纵剖面交汇处测点A16（图5（b））的纵向应力值，σp=66.53 MPa；σ100的计算方法与 σ0类似，只是需采用带有上层建筑的对应剖面，剖面的垂向惯性矩取Iy整体，中和轴高度取Zn整体，得到主甲板距中和轴的垂向距离为Z2，理论计算得到 σ100=38.58 MPa。根据式（6），即可计算得到该船上层建筑的有效度 η=0.315。