基于GEKO 湍流模型的JBC 流场数值模拟

许辉，日野孝则，陈作钢*

1 上海交通大学 海洋工程国家重点实验室，上海 200240

2 上海交通大学 船舶海洋与建筑工程学院，上海 200240

3 横滨国立大学 工学研究院，日本 横滨 240-8501

0 引 言

在船舶水动力性能预报中，除经典的船模试验和经验方法外，计算流体力学（computational fluid dynamics，CFD）方法也得到了广泛应用。在黏性作用和湍流效应不可忽略的流场中， N-S 方程是流体运动的控制方程。雷诺平均纳维-斯托克斯（Reynolds-averaged Navier-Stokes， RANS）数值模拟方法是采用经验性较强的湍流模型来对平均后的N-S 方程进行封闭，是目前工程计算中最常用、也最经济的N-S 方程数值求解方法。

SSTk-ω 湍流模型具有良好的壁面距离自适应性和逆压梯度流预报能力，但因其在构造过程中引入了经验性参数，使得湍流模型不具有普适性。Menter[1]提出了GEKO（Generalizedk-ω）湍流模型的构造思路，该模型在SSTk-ω 湍流模型的基础上，通过引入和调整不同的流动控制参数拓展了其适用范围。

JBC（Japan bulk carrier）是一种设计装备有导管型节能装置的好望角型散货船，被作为2015 东京CFD 研讨会的测试船型。Hino 等[2]对JBC 船型进行拖曳水池试验及风洞试验，测定了船体阻力及伴流场数据，并给出了JBC 船型CFD 计算的相关建议。随后针对2015 东京CFD 研讨会提交的JBC 算例，Hino 等[3]又进行了系统、全面的分析，结果显示各类CFD 方法在阻力预报方面表现均相对较好，不同的湍流封闭方法对伴流场的预报影响均较明显。Sun 等[4]、Lidtke 等[5]和Schuiling等[6]均采用传统的两方程模型对包含和不包含节能导管的JBC 流场进行了数值模拟，结果显示船体阻力预报数据与试验结果吻合良好，伴流预报给出的舭部纵向涡强度偏小。 Korkmaz[7]采用各向异性的EASM 模型对包含和不包含节能导管的JBC 流场进行了数值模拟，结果显示船体阻力预报结果略小于试验数据，而伴流预报中的舭部纵向涡强度则略大于试验数据，整体来说吻合较好。除了采用传统的经典湍流模型外，也尝试采用其他数值方法对JBC 流场进行了相关研究。Bensow 等[8]尝试采用部分平均方法（partially averaged Navier-Stokes，PANS）对JBC 流场进行了数值预报，其通过采取调整控制参数的方式来控制RANS 方法的应用范围，结果显示随着RANS 计算范围的减小，船体的黏性阻力逐渐减小，整体的阻力预报也逐渐偏小，船尾伴流场的预报结果与单纯的RANS 方法相近，认为混合方法中的近壁湍流场并没有及时转捩和发展。Queutey 等[9]采用分离涡模拟-剪切应力输运（DES-SST）方法对JBC 模型的流场进行了瞬态计算，结果表明JBC 的舭部涡是由一些强非定常性的湍流相干结构叠加而成，DES 方法通过还原该类涡结构得到了与试验结果一致性很好的船尾湍动能分布。随后，Kornev 等[10]同样采用混合雷诺平均-大涡模拟（RANS-LES）方法对JBC 流场进行了数值模拟，计算结果显示采用混合方法预报的摩擦阻力Cf明显偏小，而压差阻力Cp明显偏大，同时还研究分析了船体附近湍流结构的发展过程，得到了相比RANS 方法与试验结果吻合更好的伴流场速度及湍动能分布预报数据。总体而言，JBC 船型作为一种标准算例已进行过大量研究，是验证GEKO 湍流模型性能的良好算例。

本文将阐述GEKO 湍流模型的部分构造理论并采用JBC 船型进行计算验证，以检验构造思路的可行性和新模型对工程CFD 计算的适用性，为湍流模型工程应用的改进提供参考。

1 RANS 数值模拟理论

1.1 控制方程

在船舶水动力性能数值预报中，在流体黏性和湍流作用不可忽略的条件下，流动现象控制方程主要采用三维不可压缩黏性流动的RANS 方程组：

式中：ui，uj为瞬时速度分量；xi，xj（i，j=1，2，3）为3 个方向的空间坐标；ρ 为水的密度；p为压力；ν 为运动黏性系数；fi为体积力；t为时间；有上划线的物理量为平均值，有单引号的物理量为脉动值。方程右端第3 项为不封闭项，表现为2 个脉动速度分量的统计相关：

也即雷诺应力，是湍流模型理论的核心。

1.2 SST k-ω 湍流模型

涡黏湍流模型采用Boussinesq 涡黏假定[11]来表达雷诺应力，将脉动量的统计相关表达为平均量的函数：

式中：µT为动力涡黏系数，相应的运动涡黏系数νT=µT/ρ；δij为Kronecker 算子；k为单位流体质量湍动能；S¯i j为平均应变张量。涡黏湍流模型作为线性各向同性湍流模型，构造简单，计算中鲁棒性强，在工程上得到了广泛应用。

引入涡黏假定后，湍流模型理论的核心转变为封闭涡黏系数µT。

Menter[12]在大量工程试验和计算的基础上提出了一种经验方法，即将标准k-ε 模型[13]与Wilcoxk-ω 模型[14]进行混合：

式中：F1为标准k-ε 模型与Wilcoxk-ω 模型的混合函数； φ1为Wilcoxk-ω 模型中的任意封闭系数；φ2为标准k-ε 模型中的任意封闭系数； φ为混合后的任意封闭系数。通过封闭系数混合，可以得到BSL （Baseline）模型：

式中，β*，β，σk，γ，σω，σω2均为经验性封闭系数；µ为流体动力黏性系数。

SSTk-ω 湍流模型在BSL 模型的基础上重定义涡黏系数µT：

式中：a1为经验系数；Ω为涡量大小；F2为修正剪切应力输运效应的函数。式(6)～式(8)即为SSTk-ω模型的k方程、ω 方程和涡黏系数封闭式。相比Wilcoxk-ω 模型和标准k-ε 模型，SSTk-ω 模型在逆压梯度流中有着良好的预报能力，具有壁面距离自适应性，在工程计算中运用非常广泛。

1.3 GEKO 湍流模型

Menter[1]根据试验和工程计算经验提出，湍流模型封闭系数的细微改动会引起计算结果精确度的大幅度提升或是恶化，可以利用该思路为不同工程应用场景设计最适用的封闭系数。为便于进行系数调节，Menter[1]在提出GEKO 湍流模型时引入了多个调节参数，其中流动分离参数CS和旋转修正参数CRC对船舶流场的影响较大。但Menter没有公开其调节参数的构造方法，本文中CS及CRC采用的是Hino 等[15]研究中的定义。

首先，流动分离参数CS通过修正式(5)中的封闭系数 φ1来达到控制流动分离的目的。修正后的封闭系数 φ为

对比式(9)和式(5)可知，当CS= 1.75 时，φ=φ1，式(5)未进行任何修正，此时，GEKO 湍流模型等价于SSTk-ω 湍流模型；当CS= 1.00 时， φ=φ2=φ，此时，GEKO 模型的封闭系数全部为标准k-ε模型设置。在本文计算中，CS的取值在1.00～1.75之间。根据Menter[1]提供的参考算例，在其经过计算及试验数据标定的范围0.7＜CS＜ 2.5 内，随着CS的增大，边界层流动对逆压梯度应该逐渐敏感，从而流动分离也随之加剧。

GEKO 模型中，旋转修正参数CRC的设计思路源于Hellsten[16]对原始SSTk-ω 模型的修正，目的是提高SSTk-ω 模型对流动旋转和壁面曲率的敏感性。在GEKO 模型中，旋转修正参数CRC是通过将式(7)中右侧第2 项（即耗散项βρω2）乘以修正函数F4来实现对模型的控制，F4定义为

其中：

式中：Ri为用于曲面流动修正的Richardson 数；S为平均应变率；为平均涡量张量。式(10)中，旋转修正参数CRC主要用来表达修正幅度，不同的CRC会对结果造成不同程度的影响[17]，Hellsten建议CRC取为3.6。本文的CRC取值在0～3.6 之间。通过引入CS和CRC，应用于船舶流动的GEKO 湍流模型即构造完成。不过，模型参数对不同流动工况的适用性还需要进行大量的研究来予以确定，本文只进行了初步的尝试。

2 数值模拟

2.1 几何模型

本文以JBC 船型为研究对象对肥大船型进行GEKO 湍流模型计算测试，模型示意图如图1所示。JBC 船型的主尺度如表1 所示。计算中，以光体模型为计算对象，数值计算和对比阻力试验均在缩尺比为1∶40 的模型尺度进行，对应的试验数据来自日本海上技术安全研究所（national maritime research institute，NMRI）的系列试验[2]。

图1 JBC 船体模型示意图Fig. 1 Schematic diagram of the JBC bare hull model

表1 JBC 船型主尺度Table 1 Main dimensions of JBC ship

2.2 网格生成

计算网格采用O-O 型拓扑全结构网格，由商业软件Pointwise生成，计算域范围为-1.5 ≤x/Lpp≤ 4.5，-2.0 ≤y/Lpp≤ 0，-2.0 ≤z/Lpp≤ 0，如 图2 所示。计算域网格单元总数约为142.5 万。为解析计算近壁面处边界层的分离等流动细节，第1 层网格节点被设置于y+～1 的空间位置，垂向网格增长率设置为1.1。船艉部分的网格分布如图3 所示。

图2 计算域及边界条件示意图Fig. 2 Schematic diagram of computational domain and boundary conditions

图3 JBC 船艉部分网格示意图Fig. 3 Grid near the stern of JBC ship

2.3 求解器及计算设置

数值计算采用SURF ver. 7 求解器[18]，该求解器为基于有限体积法的三维不可压缩流动RANS 方程数值求解器，其采用二阶迎风格式离散动量方程，同时采用人工可压缩方法处理压力速度耦合。计算中，来流的雷诺数与试验中相同，取以垂线间长Lpp为特征长度的雷诺数，即Re=7.46 × 106。试验中采用的弗劳德数Fr= 0.142。为集中考察GEKO 湍流模型的计算效果，自由面采用对称条件，略去兴波阻力的影响。

在计算过程中，流动分离参数CS和旋转修正参数CRC各有3 种取值，所有的计算设置如表2所示。

表2 各工况对应参数设置Table 2 Parameter setting of varying cases

根据Menter 的计算标定，流动分离参数CS的取值可以在0.7 ＜CS＜ 2.5 范围内选取。当CS= 1.75时，GEKO 湍流模型等价于SSTk-ω 湍流模型，即C3，C3R1，C3R2 是在SST 模型的基础上进行的不同程度的CRC修正；当CS= 1.00 时，GEKO 模型封闭系数全部为标准k-ε 模型设置，即C1，C1R1，C1R2 是在标准k-ε 模型的基础上进行的不同程度的CRC修正；当CS= 1.5 时，GEKO 模型为过渡模型，即其既不是SSTk-ω 模型，也不是标准k-ε模型。流动分离参数CS的取值可以超出1.00～1.75 范围，以进一步抑制或者加强湍流模型对流动中逆压梯度的敏感性，但从物理意义上来说，因其无既有模型可以对比，故本文暂不涉及。

对于CRC的取值，当CRC= 3.6 时，GEKO 湍流模型采用Hellsten[16]建议的旋转效应修正幅度；当CRC= 0 时，GEKO 模 型 采 用 无 旋 转 效 应 的 修正；当CRC= 2.75 时则为过渡值，用于考察不同修正幅度对计算结果的影响。

3 计算结果对比及分析讨论

3.1 阻力系数对比

在阻力系数对比中，总阻力系数Ct由摩擦阻力系数Cf和黏压阻力系数Cp这2 部分组成，并由数值模拟计算直接得出这2 部分的结果。试验结果中的Cf由ITTC 1957 经验公式给出，Ct由试验[2]测量的形状因子1+k=1.314 与Cf相乘获得。试验及所有的数值模拟结果如图4 所示。

图4 数值预报阻力分量与试验数据对比Fig. 4 Comparisons between resistance components of numerical predictions and experimental data

1） 流动分离参数CS作用分析。

以C1，C2，C3 工况对比为例，当旋转修正参数CRC= 0 时，随着流动分离参数CS的增大，船体总阻力系数Ct也逐渐增大，其中黏压阻力系数Cp略有增大，摩擦阻力系数Cf则是显著增大。当CRC为其他取值时，Ct及其分量随CS的变化趋势相同。

从理论上分析，当船舶表面的边界层流动分离加剧时，黏压阻力应有增大的趋势，这与计算结果所表现的基本吻合，证明流动分离参数CS在黏压阻力调节方面基本合理。对于摩擦阻力部分，JBC 船型的摩擦阻力部分是随CS的增大而增大的。

在其他相关研究[15]中，KVLCC2 船型的摩擦阻力系数则是随CS的增大而减小，JBC 与KVLCC2同为肥大型船型，却表现出了与CS不同的关系。研究中所用湍流模型的理论构建和程序开发均是基于Menter 对其所设计GEKO 湍流模型的性能描述，因目前的测试算例相对有限，研究中CS所用的线性插值可能难以满足Menter 对所有模型的要求。最终，由于JBC 与KVLCC2 型线的区别，使得在构造较简单的湍流模型时表现出了不同的性能。

2） 旋转修正参数CRC作用分析。

以C3，C3R1，C3R2工况对比为例，此时CS= 1.75，GEKO 模型等价于进行不同CRC修正的SSTk-ω模型。当流动分离参数CS保持恒定时，随着旋转修正参数CRC的增大，总阻力系数Ct几乎没有变化，其中摩擦阻力部分略有减小，黏压阻力部分略有增大。当CS为其他取值时，总阻力系数Ct及其分量也有相同的变化趋势。总体而言，当CS恒定时，各种CRC设置下的阻力预报结果变化不大。

在其他研究[15]中，对于阻力系数与CRC的关系， KVLCC2 船型也表现出了与JBC 船型相同的变化趋势。从理论的角度分析，对于肥大型船，湍流模型针对流动旋转效应和船体几何曲率的敏感性所产生的阻力影响可能很有限。

3.2 船尾伴流场及压力分布对比

GEKO 模型的参数设置会对流场细节造成一定的影响。对于JBC 船型，桨盘面位于x/Lpp= 0.986 4处，在试验中对该处的伴流场进行了测量[2]，如图5所示。各参数设置下的数值模拟结果如图6 所示。肥大型船桨盘面的典型特征是由纵向涡引起的伴流扭曲，这在所有计算结果中均有体现。湍流模型的选取是决定船尾伴流场的关键因素，采用涡黏假定的各向同性线性湍流模型预报的纵向涡钩状低速区通常小于试验测定值[3]。不同设置下GEKO 模型预报的船尾附近压力分布及伴流场分布如图7 所示。图中，船体表面为无量纲压力系数P的分布。

图5 试验中桨盘面处（x/Lpp=0.986 4）伴流场速度分布Fig. 5 Velocity distribution of wake field at the propeller plane(x/Lpp=0.986 4)

图6 数值预报的桨盘面(x/Lpp = 0.986 4)处伴流场速度分布对比Fig. 6 Comparisons of velocity distribution of wake fields at the propeller plane (x/Lpp = 0.986 4) by numerical prediction

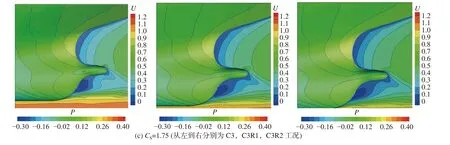
图7 各参数设置下船艉压力系数及伴流场对比Fig. 7 Comparisons of the pressure distributions and wake fields near the stern at varying parameter settings

式中：p∞为来流压力；U∞为来流速度；g为重力加速度。船尾附近为中纵剖面的无量纲速度U的分布，其中U=u/U∞，u为流场的纵向速度分量。

1） 流动分离参数CS作用分析。

以C1，C2，C3 工况对比为例，当CRC= 0 时，随着CS的增大，图6 所示桨盘面伴流场的钩状低速区明显增大，但在各种设置下均未捕获到试验中U= 0.2 的低速区。总体而言，当CS= 1.75 时，数值计算结果与试验数据的吻合程度最高。相对应的，图7 中纵剖面上的低速区随着CS的增大也有增大趋势；由船体压力分布来看，船体后肩部舭部低压区的面积是逐渐增大的，艉部高压区的变化则相对较小，舭部附近的等压线随着CS的增大逐渐汇集，因而从舭部到船艉的逆压梯度随着CS的增大具有增大的趋势，从而加剧了流动分离。当CRC为其他取值时，数值预报的结果也有类似的变化趋势。

从理论上分析，随着CS的增大，GEKO 模型对逆压梯度更加敏感，流动分离则应更加剧烈，因而必然会对伴流场产生明显的影响。而船体后肩处低压区的扩散很可能是因为流动分离的加剧削弱了船艉压力的恢复，从而导致黏压阻力增大。

在其他研究[15]中，KVLCC2 船型随CS也有类似的变化趋势，该船型与试验结果吻合最好的桨盘面伴流场出现在CS=1.85 时，超出了本文CS的取值范围。经对比可知，尽管当CS＞1.75 时没有既有的湍流模型可以对比，但仍有进一步研究的必要。

2） 旋转修正参数CRC作用分析。

以C3，C3R1，C3R2 工况对比为例，此时，GEKO模型在SSTk-ω 模型的基础上进行的CRC修正。当CS= 1.75 时，随着CRC的增大，图5 中桨盘面伴流场的钩状低速区逐渐增大并产生轻微的上移和向中纵剖面的靠拢。总体而言，当CRC= 3.6 时，GEKO 模型预报的桨盘面伴流场与试验数据的吻合程度最高。而图6 所示纵剖面上的伴流场低速区随CRC的变化则不明显，主要集中在桨帽附近；由船体压力分布来看，船体舭部低压区随着CRC的增大有面积增大的趋势，同时艉部的高压区几乎没有变化，舭部附近的等压线随着CRC的增大逐渐汇集，而其他区域的变化则不明显。由于船体舭部的曲率较大，在该区域的流场细节随CRC变化明显的同时，其他区域几乎没有变化，表明CRC的增大改变了模型对几何曲率的敏感性。当CS为其他取值时，其数值预报结果也有类似的变化趋势。对比来看，尽管CRC对JBC 船型阻力预报结果的影响有限，但对伴流场预报结果的影响则相对明显。

在其他研究[15]中，KVLCC2 船型桨盘面伴流场的低速区域范围随CRC的变化不明显，主要表现为低速区的轻微上移。从理论上分析，随着湍流模型对流动旋转效应和船体几何曲率敏感性的增大，很可能会导致肥大型船舶的纵向涡强度增大，进而导致船体舭部区域的低压区域扩散和黏压阻力的轻微上升。

4 结 论

湍流模型理论中包含有大量的量纲分析过程和经验性因素，在很大程度上还没有触及到湍流的物理机理本质，因而不具有普适性。然而，在数值计算中若根据实际工况调整湍流模型计算参数的设定，采用经济的RANS 方法仍有可能使计算获得相对合理、精确的预报结果，而采用GEKO湍流模型通过设定新参数来对传统湍流模型的封闭系数进行系统性调节是一种快捷的方法。本文尝试将GEKO 模型应用到了JBC 船型的流场数值预报。文中所构造的GEKO 湍流模型引入了流动分离参数CS和旋转修正参数CRC，用于调节流动分离强度和流动旋转效应。CS和CRC对数值计算的影响需要通过大量的数值试验进行测试，本文仅针对JBC 船型的流场预报进行了初步的尝试，主要结论如下：

1） 对于JBC 船型的阻力预报，CS的增大会导致摩擦阻力的显著增大和黏压阻力的小幅增大；CRC对船体阻力的影响较小，CRC的增大会导致摩擦阻力的略微减小和黏压阻力的略微增大，总阻力值基本保持不变。

2） 对于JBC 船型的伴流场预报，CS和CRC的影响均比较明显。随着CS的增大，桨盘面伴流场的钩状低速区会产生相应程度的增大，中纵剖面的低速区也会产生相应程度的增大；随着CRC的增大，桨盘面低速区在增大的同时会产生轻微的上移和向中纵剖面的靠拢，而中纵剖面的伴流场变化不明显。

3） 对于JBC 船型的船艉压力预报，CS的增大会导致船体后肩低压区面积的增大，进而削弱船艉的压力恢复并增大黏压阻力，同时，还会增大由舭部至船艉的逆压梯度，加剧流动分离；CRC的增大则主要会导致几何曲率较大舭部区域的流场细节变化，其他区域的变化则不明显。

4） GEKO 模型的不同参数设置对数值计算结果具有直接影响，可在一定程度上提高数值预报适用性和精确度的潜力。

在GEKO 湍流模型新参数的合理选取和对不同计算工况的适应性方面，今后仍需采用大量的数值计算进行探索。